Межбанковский клиринг
Страница 8
Параметр 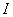 характеризует импортную незамкнутость системы: если бы пользователи клиринга были тесно связаны только между собой, то
характеризует импортную незамкнутость системы: если бы пользователи клиринга были тесно связаны только между собой, то 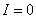 . Для страны в целом – это средства оплаты экспорта-импорта и, значит,
. Для страны в целом – это средства оплаты экспорта-импорта и, значит, 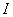 можно определить из данных статистики, если клиринг охватывает всю республику. Для группы банков – это обслуживание входа-выхода средств вне этой группы. Экономия вследствие клиринговости равна:
можно определить из данных статистики, если клиринг охватывает всю республику. Для группы банков – это обслуживание входа-выхода средств вне этой группы. Экономия вследствие клиринговости равна:
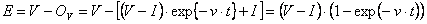
Доход от такой экономии пропорционален рыночной процентной ставке 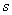 и времени
и времени 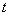 .
.
Подсчитаем интегральный эффект от клиринга. Эффект - разность дохода и убытка:
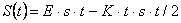 (2.6)
(2.6)
Оптимизация этой функции равносильна оптимизации следующей функции:
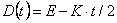 (2.7)
(2.7)
2.3. Решение задачи и его анализ
При каком-то значении 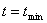 экономия достигает максимума. Для определения этого значения возьмем производную функции
экономия достигает максимума. Для определения этого значения возьмем производную функции 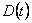 по
по 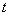 и приравняем ее к нулю. Вычисляем производную:
и приравняем ее к нулю. Вычисляем производную:
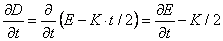
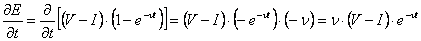
Теперь решаем уравнение:
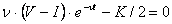
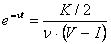
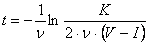
Для того, чтобы убедиться, что найденная точка является точкой глобального максимума функции интегрального эффекта от применения клиринга 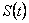 , покажем, что эта функция является вогнутой (выпуклой вверх), для чего исследуем знак второй производной функции
, покажем, что эта функция является вогнутой (выпуклой вверх), для чего исследуем знак второй производной функции 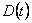 :
:
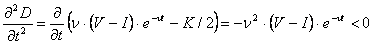
Окончательно получим:
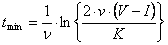 (2.8)
(2.8)
или с учетом (5):
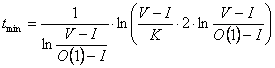 (2.9)
(2.9)
Модифицируем вид решения:
Пусть: k = K/V, т. е. k – дневная оборачиваемость средств в расчетах, определяющая, сколько рублей дневного оборота обслуживает один рубль сальдо.
е = O(l)/V, т.е. е – доля клиринговых отвлечений от валовых отвлечений при однодневном цикле.
n = 1/е – уменьшение средств, обусловленное клирингом – эффективность клиринга.
i = l/V, т.е. i – доля средств, обслуживающих в расчетах экспорт-импорт системы. Тогда
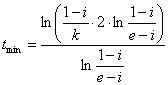 (2.10)
(2.10)
Итак, 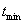 выражена через:
выражена через:
1) k – дневную оборачиваемость средств в расчетах,
2) е – долю клиринговых отвлечений от валовых отвлечений при однодневном цикле,
3) i – долю обслуживания импорта в расчетах.
Область возможного положительного эффекта от клиринга задается отрезком времени от 0 до Т. Т есть корень уравнения 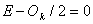 или
или
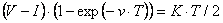
Далее ясно, что при заданной модели 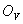 существует нижняя граница для
существует нижняя граница для 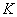 , выше которой клиринг не дает никакого эффекта. Эту границу определяет касательная к
, выше которой клиринг не дает никакого эффекта. Эту границу определяет касательная к 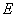 в начале координат. Прямые
в начале координат. Прямые 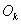 , лежащие выше касательной, не пересекаются с
, лежащие выше касательной, не пересекаются с 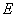 нигде, кроме начала координат. Значит, для них кривая
нигде, кроме начала координат. Значит, для них кривая 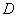 не имеет максимума не в начале координат. Указанная граница для
не имеет максимума не в начале координат. Указанная граница для 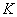 определится из условия
определится из условия
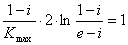 ,
,
отсюда
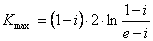 (2.11)
(2.11)
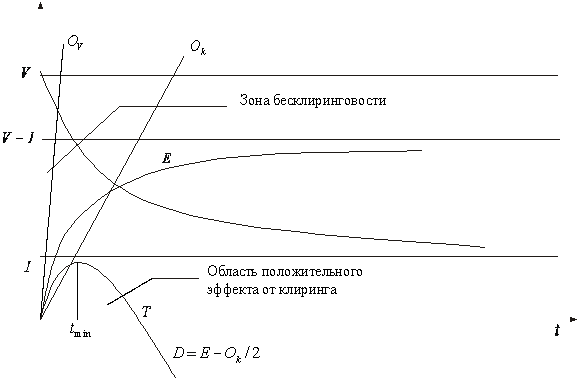 Рассмотрим также графическую интерпретацию решения (см. Рис 2.2.)
Рассмотрим также графическую интерпретацию решения (см. Рис 2.2.)
Рис.2.2. Графическая интерпретация решения.
И, наконец, подсчитаем потери от применения неоптимального лага:
Пусть dt - отклонение от 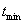 . Возникающие потери, измеряемые в сальдовых единицах, есть разность:
. Возникающие потери, измеряемые в сальдовых единицах, есть разность:
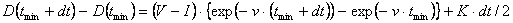 .
.
Все рассуждения, приведенные выше касались одного отдельно взятого банка, однако лаг клиринга устанавливается клиринговой палатой, составленной из представителей всех банков-участников. Поэтому, лаг, являющий оптимальным для одного банка, может быть далеким от такового для остальных банков. Поэтому для учета интересов всех участников системы предлагается следующая модель.
Пусть в клиринговой системе участвует n банков. Обозначим, как и ранее 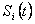 – эффект от применения клиринга с лагом
– эффект от применения клиринга с лагом 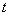 для i-го банка, вычисляемый по формуле (2.6),
для i-го банка, вычисляемый по формуле (2.6), 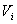 – средства i-го банка, необходимые ему для валовых взаиморасчетов (т.е. без клиринга). Тогда наиболее приемлемый для всех участников лаг клиринга рекомендуется искать, решив следующую задачу оптимизации:
– средства i-го банка, необходимые ему для валовых взаиморасчетов (т.е. без клиринга). Тогда наиболее приемлемый для всех участников лаг клиринга рекомендуется искать, решив следующую задачу оптимизации:
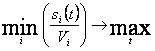 (2.12)
(2.12)
т.е. максимизируется наименьший из удельных эффектов от применения клиринга для всех банков-участников.
2.4. Статистическая оценка оптимального лага.
На основе статистической выборки, включающей в себя ежедневные данные за четыре месяца, были получены следующие оценки вышеописанных параметров: i*=0.05, k*=v*=0.42. Подставив оценочные значения в формулу (2.9), получим следующую оценку оптимального лага клиринга t* =1,538372. Таким образом, на основе вышеизложенной модели оптимизации лага клиринга можно утверждать, что оптимальным в текущих условиях является лаг в полтора дня, т.е. 36 часов.
3. ППП «Система межбанковского клиринга»
3.1. Назначение и структура пакета
ППП «Система межбанковского клиринга» является практической реализацией идеи автоматизации клирингового процесса. Пакет охватывает автоматизацию как работы самой клиринговой палаты, так и работы банков-участников клирингового сеанса. ППП содержит два функционально различных программных модуля: «АРМ оператора клиринговой палаты» и «АРМ оператора банка» и представляет собой программный продукт, построенный по схеме «клиент-сервер». Сервером является модуль «АРМ оператора клиринговой палаты», а клиентом – модуль «АРМ оператора банка». В системе всегда действует один сервер и неограниченное количество клиентов. Модуль «АРМ оператора клиринговой палаты» устанавливается на сервере клиринговой палаты, а экземпляры модуля «АРМ оператора банка» – на серверах или рабочих станциях банков-участников клирингового процесса, по одному на каждый банк. ППП обеспечивает всю необходимую функциональность для работы клиринговой палаты, однако для реального внедрения необходима существенная доработка в области сохранения целостности данных и контроля доступа к ним. Однако эта доработка может производиться независимо от существующего кода стандартными средствами СУБД. Система взаимосвязанных таблиц данных сервера реализована на базе СУБД Oracle 7.3.3 Server. Рекомендуемыми операционными системами для этой СУБД являются SCO Unix версии 5.2 и выше либо Windows NT Server версии 4.0 и выше. Клиентская часть реализована на базе СУБД Personal Oracle 7.3.3. Удаленный доступ к серверу БД реализован с помощью стандартного средства СУБД Oracle 7.3.3 – Oracle SQL* Net. Графический пользовательский интерфейс обоих модулей реализован в RAD-среде разработки приложений Borland Delphi 3.0 Client/Server для операционной системы Windows 95 или Windows NT Workstation. Полный текст исходного кода ППП «Система межбанковского клиринга» приведен в Приложении 1.