Пространственная ориентация живых организмов посредством зрительной сенсорной системы

Страница 5

1) спектр поглощения отдельного рабдомера хорошо совпадает: а) с из­вестной кривой Дартнелла (Dartnall, 1953), б) со спектром поглощения родопсина быка и кальмара, в) с кривой спектральной чувствительности, измеренной по электроретинограмме, г) с кривой спектральной чувстви­тельности, полученной при внутриклеточном отведении потенциалов;

2) спектры поглощения рабдомеров неодинаковы: так, шесть рабдомеров одной и той же ретинулы имеют максимум поглощения при 500 нм, а один — центральный — при 460 нм, что, вероятно, соответствует «синечувствительным» и «зеленочувствительным» рецепторам Буркхарда (Burkhardt, 1962);

3) после длительного засвета величина максимума поглощения при 500 нм уменьшается; вероятно, это является результатом частичного обес­цвечивания зрительного пигмента, подобно тому как это имеет место у позвоночных;

4) рабдомерам свойственно дихроичное поглощение света, причем коэффициент дихроичности поглощения равен для Calliphora 4/3, т. е. 1.33.

Последний факт представляет, пожалуй, наибольший интерес, по­скольку он позволяет вплотную приблизиться к вопросу об ориентации молекул зрительного пигмента в микровиллах рабдомеров и заслуживает более подробного рассмотрения.

Прежде всего следует вспомнить, что все животные, обладающие рабдомерным типом сетчатки (т. е. членистоногие и головоногие), способны ориентироваться в пространстве по плоскости поляризации света. В 1950 г. Аутрумом и Штумпфом была выд­винута гипотеза о том, что одиночная зрительная клетка может служить анализатором поляризованного света (Autrum

(1)

a. Stumpf, 1950), а вскоре благодаря развитию электронной микроскопии были расшифрованы осо­бенности структуры, осуществляющей эту функцию, т.е. рабдомера (Fernandez-Moran, 1956; Goldsmith a. Philpott, 1957). Появились многочислен­ные работы, подтверждающие реакцию одиночной зрительной клетки членистоногих на поворот плоскости поляризации падающего света [мухи Lucilia (Burkhardt u. Wendler, 1960), мухи Calliphora (Autrum u. Zwebl, 1962a), краба Carcinus maenas и саранчи Locusta (Shaw, 1966, 1967) 1. Стало ясно, что если ретинулярная клетка способна анализировать плоскополяризованный свет, то непосредственным анализатором его должен являться рабдомер. В свою очередь рабдомер может служить анализатором плоскополяризованного света только при наличии дихроичности коэффициента поглощения (Vries, Spoor, Jielof, 1953; Stockbammer, 1956). В 1961 г.Муди и Паррисс (Moody a. Parriss, 1961), обнаружившие, что осьминог способен различать плоскость поляризации света, попытались оценить величину коэффициента дихроичности рабдомера. При этом они исходили из пред­положения, что зрительный пигмент является структурным элементом мем­браны микровилл рабдомеров, подобно тому как это имеет место у поз­воночных (Brown, Gibbons a. Wald, 1963). Более того, Мудн и Паррисс считали (тоже по аналогии с позвоночными), что дипольные моменты мо­лекул зрительного пигмента лежат в плоскости мембраны микровилл, но ориентированы в ней хаотично (Wald, Brown a. Gibbons, 1963). В ре­зультате довольно несложного анализа Муди и Паррисс получили для от­носительного поглощения одиночной микровиллы выражение 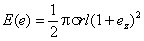где Е – относительное поглощение света; s — поверхностная плотность молекул зрительного пигмента в мембране микровиллы (число молекул на единицу площади поверхности мембраны мпкровиллы); r – радиус микровиллы; l — длина микровиллы; е — единичный вектор напряжен­ности электрического поля, имеющий составляющие по трем осям коор­динат, соответственно еx, еy и ez (в расчетах Муди и Паррисса считалось, что ось микровиллы совпадает по направлению с осью z).

Если свет распространяется вдоль оси у, которая параллельна опти­ческой оси омматидия, то он имеет две составляющие электрического век­тора — еx и ez . Дихроизм поглощения определяется отношением относитель­ных поглощений для двух составляющих еx и ez , а в случае опытов с пово­ротом плоскости поляризации света для двух положений вектора е, т. е. когда он параллелен оси z, (или, что то же самое, оси микровиллы) – Е|| и когда он перпендикулярен ей – Е^.

Очевидно, что для е, параллельного ocи z, получается |e| = ez = 1, и равенство (1) дает

	(2)

Соответственно для е, перпендикулярного оси z (т. е. для е, параллель­ного оси х), имеем

|e| = ex = 1, а ez = 0;

(3)

тогда

Коэффициент дихроичности поглощения (который по определению больше единицы) определяется отношением большего относительного поглощения (Е||) к меньшему (Е^), т. е. равен:

(4)

что и было получено Муди и Парриссом.

Однако значение коэффициента дихроичностп поглощения, получен­ное Лангером и Тореллом (Langer a. Thorell, 1966), меньше 2, а именно 4/3. Возможно, что причина этого заключается в том, что не все молекулы зрительного пигмента лежат в плоскости мембраны, что, как по­казали Уолд, Браун и Джиббонс, имеет место для мембран дисков на­ружных сегментов позвоночных (Wald, Brown a. Gibbons, 1963). В этом случае в расчеты Муди и Паррисса Грибакин (1969) предлагает внести поправку. Согласно этой поправке, следует считать, что дипольные моменты части молекул зрительного пигмента ориентированы перпендику­лярно поверхности мембраны. Обозначим поверхностную плотность мо­лекул с дипольными моментами, лежащими в плоскости мембраны, через ss, а поверхностную плотность молекул с дипольными моментами, ориенти­рованными перпендикулярно поверхности мембраны, через sr (будем называть их радиальными дипольными моментами, так как эти моменты направлены по радиусам микровилл). Очевидно, что общая поверхностная плотность молекул зрительного пигмента равна s = ss + sr . При этом раз­личным положениям плоскости поляризации световой волны (т. е. различ­ным ориентациям вектора е, который перпендикулярен плоскости поля­ризации и лежит в так называемой плоскости колебаний электромагнит­ной волны) соответствуют и различные относительные поглощения молекул, входящих в ss , и молекул, входящих в sr. Так, для е, параллельного оси z, получим

Es^ = pssrl, Er|| = 0

(Еr || равна нулю, так как е параллельно оси z и, следовательно, перпендикулярно плоскости ХОУ, параллельно которой лежат радиально направ­ленные моменты).

Для е, перпендикулярного оси z, получим