Математическое моделирование биосинтеза продуктов метаболизма

Введение.

МЕТАБОЛИЗМ – греческое слово metabole, означающее перемена, превращение.

В физиологическом смысле метаболизм – это промежуточный обмен, т. е. превращение определенных веществ внутри клеток с момента их поступления до образования конечных продуктов (напр., метаболизм белков, метаболизм глюкозы, метаболизм лекарственных препаратов).

С точки зрения промышленной биотехнологии метаболизм – это образование в процессе роста и развития клеток ценных биохимических продуктов – некоторые из них выделяются в среду (внеклеточные продукты), некоторые накапливаются в биомассе (внутриклеточные продукты). С помощью метаболизма получают антибиотики, молочную и лимонную кислоту, пищевые консерванты и многие другие продукты.

В естественных условиях метаболизм настроен так, чтобы производить минимальное количество необходимых метаболитов. Промышленное производство, направленное на получение максимальной прибыли, такая ситуация никак не устраивает. Поэтому, для максимизации прибыли необходимо произвести оптимизацию следующих технологических параметров:

– выхода продукта в расчете на потребленный субстрат;

– концентрация продукта;

– скорость образования продукта.

Оптимизация технологии биосинтеза метаболитов состоит из следующих основных этапов [5]:

1) Первоначальная селекция штамма микроорганизмов;

2) Определение оптимальных значений температуры, рН, тоничности и потребности в кислороде;

3) Определение оптимального режима питания и накопления биомассы;

4) Изменение генетической структуры организма для увеличения образования продукта.

Разработка 3-его этапа, непосредственно связана с биосинтезом. Для нахождения режима питания и накопления биомассы, оптимального для биосинтеза метаболитов необходимо математическое описание процесса [1,2,3,4]. Кроме нахождения оптимальных условий проведения процесса, математическая модель используется для автоматизации биосинтеза, что в современной биотехнологической промышленности не менее важно.

Прежде чем приступить, к описанию моделей приведем принятые обозначения основных количественных характеристик процесса биосинтеза.

Кинетические характеристики процесса биосинтеза.

Обычно состояние процесса определяется следующими основными параметрами:

– концентрация биомассы микроорганизмов – Х, г/л;

– концентрация питательной среды – субстрата (или его основного компонента) – S, г/л.

– концентрация продукта – P, г/л.

Кинетические характеристики процесса отражают скорость протекания биохимических превращений. Эти превращения, естественно, отражаются на всех указанных выше параметрах процесса – биомассе, продукте и субстрате.

Важным показателем процесса является скорость роста биомассы. Для описания скорости роста используется такая характеристика, как общая скорость роста – QX:

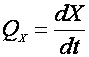(1).

Больший интерес для характеристики интенсивности роста представляет не величина QX, а удельная скорость роста в пересчете на единицу биомассы (ведь рост биомассы пропорционален концентрации клеток). Она обозначается буквой m:

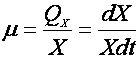(2).

Размерность величины m – [1/ч].

Рассмотрим теперь второй параметр процесса ферментации – концентрацию субстрата S. По аналогии с ростом биомассы, можно ввести кинетическую характеристику – скорость потребления субстрата QS:

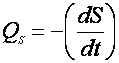(3).

Знак ‘–‘ обозначает, что скорость потребления положительна, когда концентрация субстрата в среде падает (т.е. скорость изменения концентрации отрицательна).

Аналогично, удельная скорость потребления субстрата, которую обозначим малой буквой qS, равна:

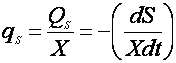(4).

При биосинтезе метаболитов, наряду с ростом биомассы, происходит накопление в среде продукта метаболизма (его текущая концентрация – Р).

Общая скорость биосинтеза продукта метаболизма QР в периодическом процессе равна:

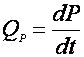(5).

Удельная скорость биосинтеза продукта единицей биомассы обозначается qР и равна:

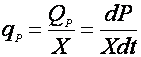(6).

Для математического описания биосинтеза продуктов метаболизма различными исследователями было предложено много различных моделей. Все эти модели можно разделить на следующие группы:

1) Математические модели кинетики биосинтеза продуктов метаболизма как функция от удельной скорости роста;

2) Субстрат-зависимые модели кинетики биосинтеза продуктов метаболизма;

3) Модели, основанные на концепции возраста культуры микроорганизмов .

Во время биосинтеза происходит также процесс уменьшения количества метаболитов, для описания этого феномена были предложены модели деградации (инактивации) продуктов метаболизма.

Математические модели кинетики биосинтеза продуктов метаболизма как функции от удельной скорости роста.

Математический параметр – удельная скорость роста m – послужил основой составления многих математических моделей биосинтеза продуктов метаболизма. Процессы биосинтеза продуктов издавна делят на два больших класса – связанные с ростом и не связанные с ростом. В качестве примера первого класса можно назвать биосинтез конститутивных ферментов клетки, а второго класса - биосинтез многих антибиотиков, интенсивный синтез которых происходит после прекращения роста микроорганизмов.

Удельная скорость биосинтеза связанных с ростом продуктов может быть выражена простым соотношением [5]:

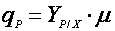(7),

где YP/X – выход единицы продукта с единицы биомассы: (dP/dX).

Более сложное выражение было предложено Людекингом и Пайри [6]:

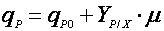(8),

где qP0 – эмпирическая константа.

В этом случае биосинтез продукта, с одной стороны, ассоциирован с ростом, а, с другой, осуществляется покоящейся клеткой [7]. Модель (8) впервые была предложена для описания синтеза молочной кислоты.

Есть ряд уравнений, учитывающих нелинейный характер связи qP и удельной скорости роста:

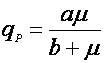(9),

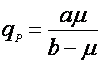(10),

где а и в – эмпирические константы.

Рис. 1. Форма зависимости qР(m) для уравнений (9) и (10).

На рис. 1 показаны графики функций (9) и (10), эти уравнения дают выпуклую (9) и вогнутую (10) кривые, выходящие из нуля, но эти функции могут иметь также дополнительный свободный член qP0:

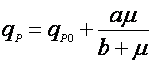(11),

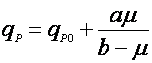(12).

Тогда графики функций (11) и (12) в отличии от (9) и (10) выходят не из нуля, а из некоторой точки qP0 на оси y, что продемонстрировано на рис. 2.

Рис. 2. Форма зависимости qР(m) для уравнений (11) и (12).

Возможны также эмпирические уравнения типа [8,9]:

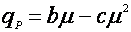
(13),

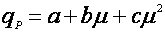
(14).

где а, b, с – эмпирические константы.