Анализ финансовых результатов на примере магазина «Кош»
Страница 18
Q2 – остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
По заданному уровню значимости l и числу степеней свободы k1 =m-1 и k2 = n-m по таблице F-распределения находится значение Fтабл и сравнивается с расчетным Fp :
если Fp > Fтабл, то нулевая гипотеза Н0 отвергается и уравнение регрессии (модель) считается значимым;
если Fp < Fтабл, то нет основания отвергать нулевую гипотезу Н0.
Значимость коэффициентов регрессии проверяется с помощью t-критерия, значение которого рассчитывается по формуле:
t = r / Sr = r n-2 / 1 – r 2
где r – коэффициента уравнения регрессии;
Sr - среднеквадратическое отклонение r.
При заданном уровне значимости l и числе степеней свободы k = n – m – 1 определяется табличное значение t – критерия и сравнивается с расчетным tp : - если tp > tpасч коэффициент регрессии является значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
Оценка влияния отдельных факторов на основе модели.
Коэффициенты регрессии являются именованными числами, выраженными в разных единицах измерения. Поэтому трудно, а иногда невозможно сопоставить факторы Х по степени их влияния на зависимую переменную Y. Для устранения этого недостатка в практике экономического анализа используются следующие коэффициенты:
коэффициент эластичности Э;
бета – коэффициент, b;
дельта – коэффициент, ∆. Коэффициент эластичности имеет вид: Эi = bi * x i / y ( 27 )
где bi – коэффициент модели при i– факторе; х i – среднее значение i – го фактора;
у – среднее значение зависимой переменной.
Коэффициент эластичности i – фактора Х i говорит о том, что при отклонении его величины от среднего значения хi на 1%, и при фиксированных на постоянном уровне значениях других факторов, входящих в уравнение, объясняемая переменная Y отклониться от своего среднего значения y на э i процентов. Иначе, - изменение значения фактора Х i на 1% от его средней величины х i, приводит к изменению значения объясняемой переменной на э i процентов от ее средней величины.
Бета – коэффициент имеет вид: b i = b i * S i / Sy , ( 28 )
где b i - коэффициент модели при i- м факторе;
S i – оценка среднеквадратического отклонения i – го фактора;
Sy - оценка среднеквадратического отклонения зависимой переменной Y.
Бета-коэффициент при факторе X i определяет меру влияния его вариации на вариацию зависимой переменной Y при фиксированной на одном уровне вариации остальных независимых факторов, входящих в уравнение регрессии.
Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную .
Дельта-коэффициент имеет вид:
∆i = ri bi / R2 , ( 29 )
где bi – бета-коэффициент i – го фактора Хi ;
ri – коэффициент парной корреляции i – го фактора Хi и зависимой переменной Y;
R2 – коэффициент множественной детерминации.
Дельта-коэффициент позволяет оценить долю вклада каждой независимой переменной Хi в суммарное влияние всех факторов.
При корректно проводимом анализе значения ∆ - коэффициентов положительны, то есть все коэффициенты регрессии имеют тот же знак, что и соответствующие парные коэффициенты корреляции. Но в случаях сильной коррелированности факторов некоторые дельта-коэффициенты могут быть отрицательными вследствие того, что соответствующий коэффициент регрессии имеет знак, противоположный знаку парного коэффициента корреляции.
Прогнозирование на основе модели регрессии.
Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений переменной. При это перенос закономерности связи, измеренной в исследуемой совокупности в статике на динамику, не является корректным и требует проверки условий допустимости такого переноса (экстраполяции).
Ограничением прогнозирование на основании регрессионной модели служит условие стабильности или малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними.
Прогнозируемое значение переменной Y получается при подстановке в уравнение регрессии: ŷ n+k = a0 + a1 xn+1
ожидаемой величины фактора Х. Данный прогноз называется точечным. Возникает ограничение при выборе ожидаемой величины Х: нельзя подставлять значения независимой переменной xn+k , значительно отличающейся от входящих в исследуемою выборку, по которой вычислено уравнение регрессии.
Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал с достаточно большой надежностью.
Средняя ошибка линии регрессии в генеральной совокупности при значении фактора xn+k вычисляется для линии регрессии по формуле:

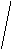 _ n _
_ n _
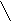 m Ŷk = Stтабл 1 / n + (xn+k – x ) 2 / å (xi - x ) 2 , ( 31 )
m Ŷk = Stтабл 1 / n + (xn+k – x ) 2 / å (xi - x ) 2 , ( 31 )
i =1
где tтабл - табличное значение t – статистики с уровнем значимости l и степенью свободы (n - 2);
S – стандартная ошибка зависимой переменной.
Границы доверительного интервала вычисляются, соответственно, как:
нижняя граница - UH(k) = ŷ n + k – m y k ;
верхняя граница – UB(k) = ŷ n + k + m ŷ k.
Средняя ошибка прогноза для индивидуального значения зависимой переменой Y от линии регрессии вычисляется по формуле:

 n _
n _
 m ŷ (xk) = Stтабл 1 +1 / n + (xn+k – x ) 2 / å (xi - x ) 2 (32 )
m ŷ (xk) = Stтабл 1 +1 / n + (xn+k – x ) 2 / å (xi - x ) 2 (32 )
i =1
Критерием прогнозных качеств оцененной регрессионной модели может служить относительная ошибка прогноза:
V = S / y , ( 33 )
где S - стандартная ошибка зависимой переменной;
y - среднее значение фактических данных зависимой переменной.
Если величина V мала и отсутствует автокорреляция остатков (то есть систематичность отклонений зависимой переменной от линии регрессии), то прогнозные качества модели высоки. Автокорреляция остатков проверяется с помощью критерия Дарбина – Уотсона, рассчитываемая по формуле:
n n
d p = å (ei - e i-1)2 / å ei2 , ( 34 )
i =1 i =1
и сравнивается с табличными значениями d1 и d2, определенными по таблице с уровнем значимости l и числом степеней свободы k = n: при dр > d2, то корреляция отсутствует.
Если построенная регрессионная модель адекватна и прогнозные оценки факторов достаточно надежны, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадет в интервал, образованный нижней и верхней границами.
3.2 Экономико – математическое моделирование прибыли ГУСП «Башхлебоптицепрома»
В корреляционной матрице дается критическое значение коэффициента корреляции на уровне 90 % при двух степенях свободы:
уровень 90 % - это надежность получаемых результатов, она задается исследователем;
две степени свободы – это количество исследуемых одновременно параметров.
Все коэффициенты корреляции, табличные значения которых, меньше критического значения коэффициента корреляции (+ 0,2920), принимается равным нулю, то есть корреляционная связь между переменными является не значимой. Качественная оценка коэффициентов корреляции осуществляется на основе шкалы Чеддока.
Проанализируем силу связи зависимой переменной Y с независимыми переменными Хi.
Целью данного исследования является построение «лучшей» модели для определения влияния составляющих затрат на изменение выручки от реализации товара на изменение прибыли, а также для прогноза прибыли на последующие 3 этапа, а именно на 3 месяца.
Для проведения исследования необходимы исходные данные. В данной задаче анализу подвергаются 7 составляющих затрат, с целью выявления их влияния на выручку от реализации товара.