Деревянные конструкции
Страница 4
7.Причины расхождения между опытными и теоретическими величинами?
Теоретические идеализированные. В опытных анизотропность свойств древесины, пороки.
Лабораторная работа № 4
Испытание клееной деревянной балки прямоугольного сечения на поперечный изгиб.
Цель работы: изучение работы клеедощатой балки.
Задачи: определить расчетную нагрузку на балку и сравнить ее с расчетной, определить модуль упругости клееной древесины, определить величины и характер распределения нормальных напряжений по высоте поперечного сечения балки, построить теоретический и экспериментальный графики прогибов балки.
1. УСТАНОВЛЕНИЕ ФАКТИЧЕСКИХ РАЗМЕРОВ ОБРАЗЦА
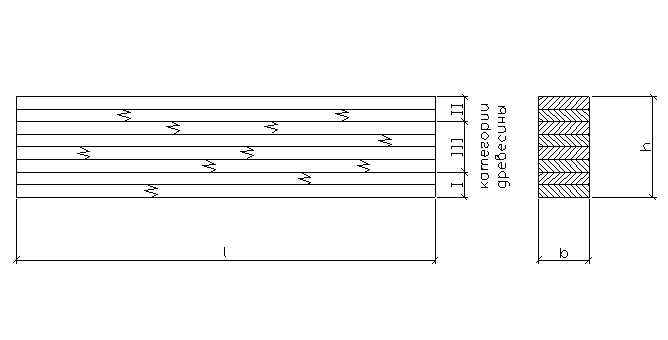Рис. 15. Клеедощатая балка прямоугольного поперечного сечения.
Исходные данные: l = 1950 мм;
h = 158 мм;
b = 50 мм.
2. СХЕМА ЗАГРУЖЕНИЯ ОБРАЗЦА И РАССТАНОВКИ ПРИБОРОВ
Рис. 16. Схема загружения балки и расстановки приборов:
1– клеедощатая балка; 2– неподвижная опора; 3– подвижная опора; 4–распределительная траверса; 5– стальной валик; 6– металлическая накладка; 7– нагруженная траверса.
3. ОПРЕДЕЛЕНИЕ РАСЧЕТНОЙ НАГРУЗКИ НА БАЛКУ
Расчетная нагрузка Р определяется исходя из расчетной несущей способности балки или достижения ею предельного прогиба.
а) из условия обеспечения прочности от действия нормальных напряжений
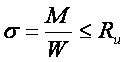
где: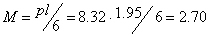 
kH×м – расчетный изгибающий момент, Н
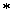м (кгссм)
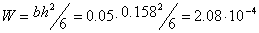
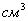– момент сопротивления поперечного сечения;
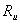– расчетное сопротивление древесины изгибу, МПа (
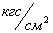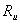) (=13 МПа)
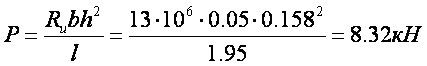
б) из условия обеспечения прочности клеевого шва от действия касательных напряжений
где: Q = P / 2=13.27/2=6.64, Н (кгс);
Sбр = b×h2 / 8=0.05×0.1582 /8=156.03 см3;
Jбр = b×h3 / 12=5×15,83/12=1643,46 см4;
bрасч = b×K – при расчете на скалывание по клеевому шву, где К=0.6 – коэффициент непроклея, принимаемый по действующим нормам.
После подстановки получим:
bрасч = b×K=0.6×5=3 см
Rck=2.1 MПА
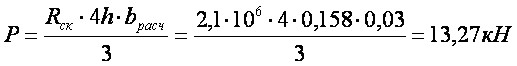
в) из условия достижения предельного прогиба
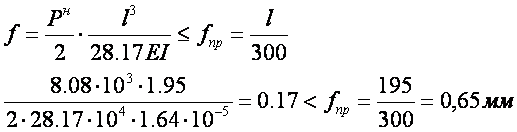
где Pn=Р/n ;( n=1.2 – усредненный коэф. надежности);
Е =104 МПа– модуль упругости древесины
После преобразования получаем:
,
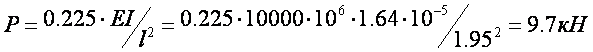где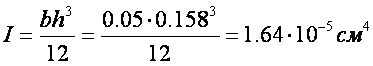 
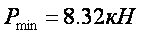
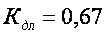
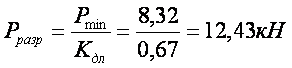
4. ИСПЫТАНИЕ БАЛКИ
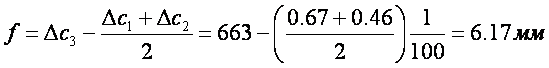
Прибор: АИД – 2М с компенсирующим устройством с выходом шкалы С*10-5
5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
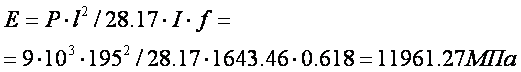
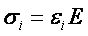
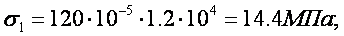
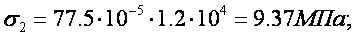
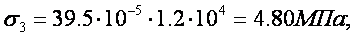
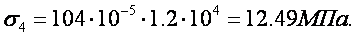
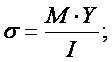
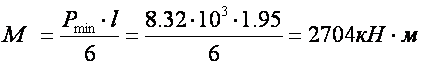
sт=13Mпа sэкс=14,4Мпа
sт=13 sэкс=12,49
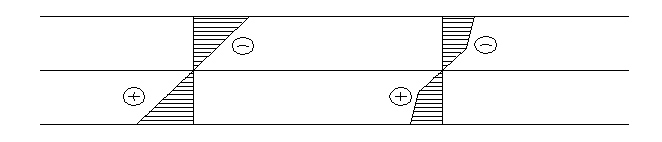
Рис. 17. Эпюра напряжений по высоте сечения балки:
6. СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ И ЭКСПЕРЕМЕНТАЛЬНЫХ ВЕЛИЧИН И АНАЛИЗ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
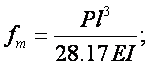
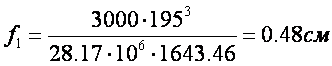
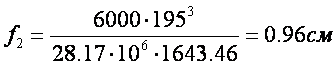
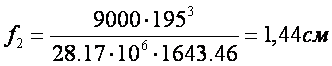
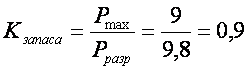
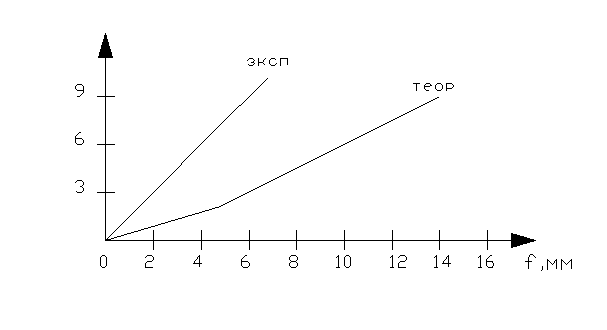
Рис.18 График прогибов балки
ВЫВОД: Экспериментальная величина прогиба значительно меньше расчетной величины в следствие в рассматриваемых конструкциях создается запас прочности (Кзапаса=0,9).
Контрольные вопросы
1. Какие требования предъявляют к древесине и клею при склеивании ?
Влажность древесины 9–12%. Не должно быть мелких пороков как сучки, косослой, гниль. Не должно быть дефектов обработки как корабление и трещины, склеиваемые поверхности должны быть свеже отфрезерованными, очищенными и плотно прилегать одна к другой.
Клеи должны быть прочными, водостойкими, долговечными, технологичными. К основным технологическим показателям клея относятся вязкость и жизнеспособность.
2. Какой метод принят для расчета деревянных конструкций, его сущность ?
Расчет по предельным состояниям. Предельным называется такое состояние конструкций за пределами которого дальнейшая эксплуотация не возможна. Два вида предельных состояний: 1)по несущей способности (прочности, устойчивости), 2) по деформациям (прогибам, перемещениям). Расчет по первому предельному состоянию производится на расчетные нагрузки, а по второму– на нормативные.
3. Как определить модуль упругости клееной древесины при изгиде?
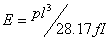, где f– прогиб образца
p– степень загружения
4. Как экспериментально определяются нормальные напряжения в балке при изгибе?
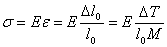
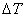– разность отсчетов; 
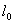– база прибора; М– цена деления прибора
5. Какие формы разрушения могут быть в клеедощатой балке?
а) разрушение по клеевому шву от действия косательных напряжений.
б) разрушение балки от действия локальных напряжений.
6. Почему экспериментальные данные отличаются от теоретических?
Т.к. древесина анизотропная и имеет пороки, а теоретические данные получены для идеализированного материала.