Консолидирование задолженности

Страница 2

Другой весьма распространенной операцией краткосрочного характера, для оценки которой используются рассмотренные формулы, является операция по учету векселей банком. В этом случае пользуются дисконтной ставкой. Одна из причин состоит в том, что векселя могут оформляться по-разному, однако чаще всего банку приходится иметь дело с суммой к погашению, т.е. с величиной FV. Схема действий в этом случае может быть следу­ющей. Владелец векселя на сумму FV предъявляет вексель банку, который соглашается его учесть, т.е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называ­ется дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую исходя из объявленной банком ставки дискон­тирования (d). Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Расчет предоставляемой банком суммы ведется по формуле:

PV == FV • (1 —f • d ), или PV = FV (1 —t/T • d), (4)

где f - относительная длина периода до погашения ссуды (опера­ция имеет смысл, когда число в скобках не отрицательно).

2. Консолидирование задолженности.

В практике нередко возникают случаи, когда необходимо заме­нить одно обязательство другим, например с более отдаленным сро­ком платежа, досрочно погасить задолженность, объединить не­сколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств ко­торая предполагает неизменность финансовых отношений сторон до и после изменения контракта.

Эквивалентными считаются такие платежи, которые, будучи "приведены" к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования к более ранней дате или, наоборот, наращения суммы платежа (ес­ли эта дата относится к будущему). Если при изменении условий принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно зара­нее определить. По существу, принцип эквивалентности следует из формул наращения и дисконтирования, связывающих величи­ны Р (первоначальная сумма долга) и S (наращенная сумма, или сумма в конце срока), Сумма Р эквивалентна S при принятой процентной став­ке и методе ее начисления. Две суммы денег S1 и S2, выплачивае­мые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S1 на S2 в этих условиях формально не изме­няет отношения сторон.

Сравнение платежей предполагает использование некоторой процентной ставки, и, следовательно, результат зависит от выбора ее величины. Однако, что практически весьма важно, такая зависи­мость не столь жестка, как это может показаться на первый взгляд. Допустим, что сравниваются два платежа S1 и S2 сроками n1 и n2 , измеряемыми от одного момента времени, причем S1 < S2 и n1 < n2. Их современные стоимости Р1 и Р2 в зависимости от размера про­центной ставки показаны на рис. 3.1.

С ростом i величина Р уменьшается, причем при i = i0 наблюда­ется равенство Р1 = Р2. Для любой ставки i < i0 Р1 < Р2. В свою оче­редь, при i > i0 Р1 > Р2. . Таким образом, результат сравнения зависит от критического (барьерного) размера ставки, равного i0. Определим величину этой ставки. На основе равенства современных стоимо­стей сравниваемых платежей

S1 S2

1 + n1 i0 1 + n2 i0

Находим

(1)

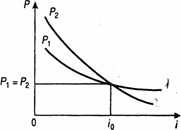
рис. 1.

Из формулы (1) следует, что чем больше различие в сроках, тем больше величина i0 при всех прочих равных условиях. Рост отноше­ния S1/S2 оказывает противоположное влияние.

Если дисконтирование производится по сложной ставке, то кри­тическую ставку найдем из равенства

S1 (1+ i0) = S2 (1+ i0)

Получим:

(2)

Принцип эквивалентности приме­няется при различных изменениях условий выплат денежных сумм.

Общий метод решения подобного рода задач заключается в разра­ботке так называемого уравнения эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-ли­бо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных обя­зательств приведение осуществляется обычно на основе простых ставок, для средне- и долгосрочных — с помощью сложных ставок. Заметим, что в простых случаях часто можно обойтись без специаль­ной разработки и решения уравнения эквивалентности.

Одним из распространенных случаев изменения условия являет­ся консолидация (объединение) платежей. Пусть платежи S1, S2, …, Sm со сроками n1, n2, …, nm заменяются одним в сумме So и сроком n0. В этом случае возможны две постановки задачи: если задается срок n0, то находится сумма So, и наоборот, если задана сумма консоли­дированного платежа So, то определяется срок n0.

При определении суммы консолидированного платежа уравнение эквивалентности имеет простой вид. В общем случае, когда n1< n2, <…<. nm , причем n1< n0 < nm , искомую величи­ну находим как сумму наращенных и дисконтированных платежей. При применении простых процентных ставок получим:

(3)

где Sj — размеры объединяемых платежей со сроками ni< n0;

Sk - размеры платежей со сроками n k > n0;

В частном случае, когда n0 > nm

(4)

При объединении обязательств можно применить и учетные ставки. В этом случае при условии, что все сроки выплат пролон­гируются, т.е. n0 > nj , находим сумму наращенных по учетной став­ке платежей:

So = å Sj (1- tj d )

В общем случае имеем

So = å Sj (1- tj d ) + å Sk (1- tk d )

Здесь tj, tk имеют тот же смысл, что и выше.

Консолидацию платежей можно осуществить и на основе слож­ных ставок. Вместо формулы (3) получим для общего случая

( n1 < nо< nm )

So = å Sj (1+ t ) + å Sk (1 + i ) (5)

Если при объедине­нии платежей задана величина консолидированного платежа So, то возникает проблема определения его срока n0. В этом случае урав­нение эквивалентности удобно представить в виде равенства совре­менных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

So (1+ n0i ) = å Sj (1+ nj i )

Отсюда

(6)

Очевидно, что решение может быть получено при условии, что Sо > å Sj (1+ nj i )

Иначе говоря, размер заменяющего платежа должен быть больше суммы современных стоимостей заменяемых пла­тежей. Искомый срок пропорционален величи­не консолидированного платежа.

При консолидации платежей на основе сложных про­центных ставок уравнение эквивалентности будет следующим:

So (1 + i) = å Sj (1+ i )

Для упрощения дальнейшей записи можно принять:

Q = å Sj (1+ i )

Тогда

(7)

Решение существует, если соблюдено условие So > Q. Для частного случая, когда Sо = å Sj при определении срока кон­солидирующего платежа вместо формулы (7) иногда применяют средний взвешенный срок:

(8)

Привлекательность этой формулы, помимо ее простоты, состоит в том, что она не требует задания уровня процентной ставки. Она дает приближенный результат, который больше точного. Чем выше ставка i, тем больше погрешность реше­ния по формуле (8).

Список литературы

1. Ковалев В.В. Финансовый анализ: Управление капиталом. Выбор инвестиций. Анализ отчетности. – М.: Финансы и статистика, 1997. –512 с.

2. Малыхин В.И. Финансовая математика.: Учеб. пос. для вузов. – М.: ЮНИТИ – ДАНА,1999.- 247 с.

3. Четыркин Е.М. Методы финансовых и коммерческих расчетов. – 2-е изд., испр. и доп. – М.: «Дело Лтд», 1995. – 320 с.