Определение и расчет параметров детонации зарядов ВВ
Определение и расчет параметров детонации зарядов ВВ
1. Цель лабораторной работы
Целью работы является: изучение современных методик исследования быстропротекающих процессов, анализ способов теоретического прогнозирования параметров детонации и определение параметров детонации и метательной способности зарядов из БВВ.
2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДЕТОНАЦИИ ЗАРЯДОВ ВВ
2.1. Основные явления, определяющие детонацию
Взрывчатые вещества (ВВ) — это вещества, способные к экзотермическому превращению, .которое передается от реагирующего слоя .к близлежащему, распространяясь в виде волны по всему заряду ВВ. Для того чтобы процесс, именуемый детонацией, оказался принципиально возможным, .необходимо, чтобы реакция экзотермического превращения протекала за чрезвычайно короткое время. Такие времена реакции, порядка 1 мкс, возможны лишь при очень высоких давлениях, при которых волны сжатия всегда трансформируются в ударные волны. Таким образом, детонацию можно представить себе как совокупное действие ударной волны и химической реакции, при которой ударный импульс инициирует реакцию, а энергия реакции поддерживает амплитуду волны, (скорость детонации различных ВВ составляет от 1500 до 10000 м/с), а давление непосредственно за фронтом волны — от 1 до 50 ГПа.
Процесс превращения исходного ВВ в конечные продукты взрыва можно представить следующим образом. Исходное состояние системы характеризуется начальным давлением Ро и начальным удельным объемом Vо. Под действием ударной волны ВВ сжимается и его исходное состояние (точка с. координатами Ро, Vо) скачком изменяется и соответствует точке P1 V1 динамической адиабаты. В сжатом ВВ начинается химическая реакция. Вследствие реакция выделяется тепло. При этом состояние системы будет описываться не адиабатой исходных продуктов, а адиабатой продуктов взрыва, которая лежит выше из-за выделения тепла. Графически этот процесс .представлен Р—V диаграммой на puc 1. 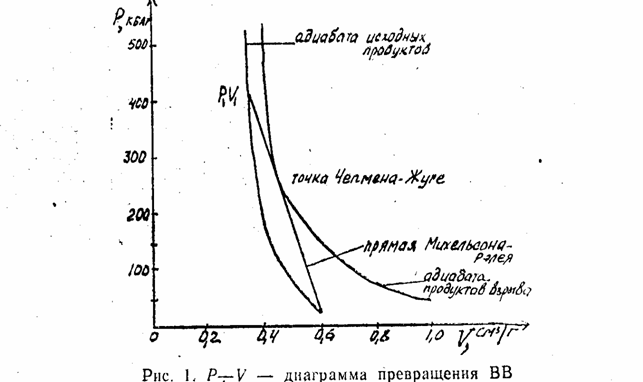
Если процесс детонации стационарен, то переход от исходного вещества к адиабате продуктов взрыва совершается по прямой линии, соединяющей точки Р1, V1 и Pо, Vо. Состояние Р1, V1 на диаграмме, отвечающее ударному фронту, распространяется по ВВ 'со скоростью детонации D.
При стационарной детонации с такой же скоростью должны распространяться и другие промежуточные состояния, соответствующие выделению той или иной доля полной энергии. Следовательно; изменение состояний в процессе химической реакции должно происходить по прямой, соединяющей точки, так как только Р1, V1 и Pо, Vо на этой прямой все промежуточные состояния распространяются по ВВ со скоростью D. Прямая равных скоростей распространения на Р—V диаграмме, по которой происходит .переход с одной адиабаты на другую — эта прямая Михельсона-Релея. Точка касания прямой Михельсона-Релея с адиабатой конечных продуктов взрыва —точка Чепмена-Жуге. Она отвечает моменту окончания химической реакции и выделению максимального количества тепла, идущего на поддержание процесса детонации.
Для полного описания процесса детонации, помимо знания давления за фронтом ударной волны и скорости детонации, необходимо знать распределение скорости потока продуктов детонации (ПД) за фронтом волны во времени U=U(t) и время существования самой волны. Зная параметры D и U=U{t}, можно, основываясь на выводах гидродинамической теории, рассчитать давление за фронтом волны Р, показатель политропы процесса п , определить во многих случаях время химической реакции т и ширину зоны химической реакции (ЗХР) — а.
Современная гидродинамическая теория детонации позволяет математически описать процесс детонации ВВ с помощью уравнений сохранения массы, импульса и энергии, уравнения состояния продуктов детонации и дополнительного уравнения, так называемого условия касания.
Уравнение состояния ПД в общем виде выглядит следующим образом:
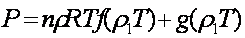
где f — функция описывает главным образом тепловое движение; g — силы, возникающие при межатомном взаимодействии.
Уравнение Лалдау-Зельдовича вида Р=Аrn имеет достаточно простой вид и с некоторыми допущения описывает состояние ПД во всем диапазоне давлений расширяющихся ПД, поэтому оно использовало для вывода соотношений, определяющих параметры детонации.
В общем виде система уравнений может быть записана следующая:
rоD=r(D-U); (1)
P= rоDU; (2)
e-eо-QV=1/2P(Vo-V); (3)
Р=Аrn (4)
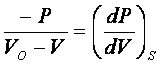 (5)
(5)
где rо и r— плотность заряда ВВ и ПД соответственно;
Vо и V — удельный объем ВВ и ПД; D — скорость детонации; U — массовая скорость ПД; e и eо — внутренняя энергия ВВ и ПД; Qv — теплота взрыва; А — постоянная; п — показатель политропы.
Заметим плотность в уравнении (4) на удельный объем
P=A*1/Vn (6)
и продифференцируем обе части данного уравнения
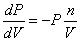 (7)
(7)
подставив данное выражение в условие касания (5), получим
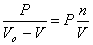 (8)
(8)
Из этого следует, что
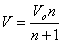 (9)
(9)
или
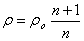 (10)
(10)
Совместным решением уравнений (1) и (2) получим уравнение прямой Михельсона-Рэлея в виде
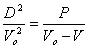 (11)
(11)
Подставив в уравнение (4) выражение (8), получим
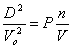 (12)
(12)
Заменив Р на его выражение из уравнения (2), получим
D/U=n+1 (13)
Используя уравнения (9) и (13), получим следующие соотношения для параметров детонации:
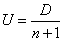 (14)
(14)
P=rоDU=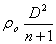 (15)
(15)
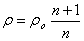 (16)
(16)
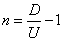 (17)
(17)
Анализ данных уравнений показывает, что для определения всех параметров детонации необходимо и достаточно измерить любые два параметра в точке Чепмена-Жуге, где заканчиваются все химические превращения.
Теоретический профиль распределения давления или массовой скорости от времени в детонационной волне, приведен на рис. 2.

Время t, отвечающее излому профиля давления — время  химической реакции, и по нему можно рассчитать ширину ЗХР-а.
химической реакции, и по нему можно рассчитать ширину ЗХР-а.
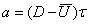 , (18)
, (18)
где 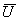 — средняя скорость потока в ЗХР.
— средняя скорость потока в ЗХР.
На практике для определения параметров детонации оказалось удобно измерять D и профиль массовой скорости U=U(t). Для измерения массовой скорости чаще всего пользуются откольным и электромагнитным методами.
2.1.1 Откольный метод определения массовой скорости ПД.
Идея откольного метода заключается в измерении . скорости движения свободной поверхности пластины, плотно прижатой к торцу заряда ВВ. Падающая детонационная волна распространяется по пластине с затухающими параметрами, при этом скорость движения свободной поверхности пластины связана с массовой скоростью волны, выходящей на эту поверхность следующим соотношением:
Wn=2Un, (19)
где W — скорость свободной поверхности пластины; Un — массовая скорость ударной волны в пластине.
| 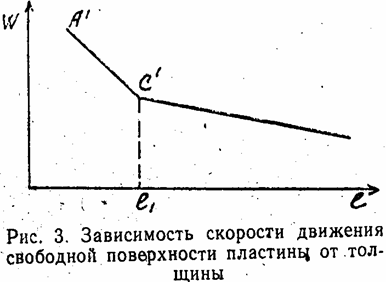 |
Затухание параметров ударной волны зависит от толщины пластины и профиля давления падающей детонационной волны, поэтому характер изменения скорости свободной поверхности от толщины отражает профиль самой волны.