Страница 3
или коэффициент текущей стоимости.
Существуют два основных метода начисления процентов: простой и сложный, которые отличаются исходной базой для определения процентов.
Простой способ начисления первоначальной суммы денег состоит в неизменности исходной базы для начисления(PV). В этом случае начальная сумма денежных средств PV при всей ее неизменности за определенный период времени, в течении которого n раз начисляются проценты, возрастает до величены 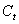 : :
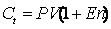
При сложном способе исходная база для начисления процента увеличивается с каждым периодом начисления, поэтому наращение по сложному проценту ускоряется.
Тогда
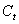 =PV(1+E) =PV(1+E)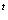
Указанные способы могут быть распространены на любую сферу финансовых операций, а формулу сложных процентов можно использовать для дисконтирования разновременных денежных потоков.
Например, если рассматривать денежные потоки разных лет, то формулу можно представить в виде
PV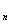 =C =C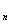  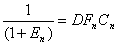 , ,
где n – количество периодов времени между датой инвестирования и датой выплаты причитающейся суммы; 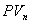 - доходность инвестирования на n периодов времени; - доходность инвестирования на n периодов времени; 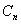 - сумма, причитающаяся к выплате через n периодов времени; - сумма, причитающаяся к выплате через n периодов времени; 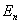 - текущая стоимость денежной суммы, которая поступит в n-м периоде времени; - текущая стоимость денежной суммы, которая поступит в n-м периоде времени; 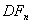 - коэффициент текущей стоимости (дисконтирования), которая будет получена в n-ный период времени или: - коэффициент текущей стоимости (дисконтирования), которая будет получена в n-ный период времени или: 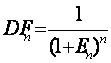
Например. Сколь денег надо инвестировать сейчас, чтобы через 5 лет получить 10000 руб. при доходности 100% годовых?
Ответ: 10000[1/(1+1)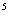 =10000(1/32)=10000*0,03125=312,5 руб. =10000(1/32)=10000*0,03125=312,5 руб.
Надо отметить, что доходность Е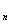 от инвестирования одной и той же суммы денег на разные сроки не обязательно будет одинаковой, а скорее всего- разной. Известно, что чем больше срок инвестирования, тем выше риск такой операции, а значит, и тем больше должна быть доходность, покрывающая его. Кроме того, ожидаемая доходность может меняться в соответствии с измерениями инфляции, уровней доходности альтернативных вариантов и инвестирования. от инвестирования одной и той же суммы денег на разные сроки не обязательно будет одинаковой, а скорее всего- разной. Известно, что чем больше срок инвестирования, тем выше риск такой операции, а значит, и тем больше должна быть доходность, покрывающая его. Кроме того, ожидаемая доходность может меняться в соответствии с измерениями инфляции, уровней доходности альтернативных вариантов и инвестирования.
На практике чаще встречаются более сложный случай, когда одноразовое инвестирование предполагает несколько возвратных платежей(притоков)в разные моменты времени в будущем.
Пример. Существует некий инвестиционный проект, который позволит получить через один год 125 тыс. руб. при ставке доходности 25% годовых, и кроме этого-150 тыс. руб. при ставке доходности 30% годовых и 160 тыс. руб. при ставке доходности 40% годовых. Какую сумму можно инвестировать сейчас в данный инвестиционный проект? Задача решается по частям для каждого инвестиционного проекта. Тогда :
PV1=125/(1+0.25)=100тыс. руб.
PV2=152/(1+0.3)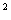 =88.76тыс. руб. =88.76тыс. руб.
PV3=160/(1+0.4) =58.31 тыс. руб. =58.31 тыс. руб.
Сложив все величины, получим ответ:
PV=PV1+PV2+PV3=100+88.76+58.31=247.07 тыс. рублей.
Таким образом, инвестируя в проект первую часть из 100 тыс. руб., получим 125 тыс. руб. через год; инвестируя в проект вторую часть из 88,76 тыс. руб., получим 150 тыс. руб. через два года; инвестируя в проект третью часть из 58,31 тыс. руб., получим 160 тыс. руб. через три года. В результате, чтобы осуществить проект, необходимо в настоящий момент инвестировать 247 тыс. руб.
Формулу дисконтирования денежных средств можно записать в виде
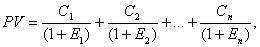
где С1, С2, Сn – поступления соответствующего периода времени от 1 до n; Е1, Е2, Еn – доходность соответствующего периода времени от 1 до n .
Надо отметить, что эта формула является базовой, используемой для определения текущей стоимости денежных поступлений от осуществления любых инвестиционных проектов.
Возвращаясь к примеру решения последней задачи, необходимо сделать одно замечание. Реализация инвестиционного проекта связана с потоками денежных средств, которые могут быть либо независимыми, т.е. не связанными с определенными финансовыми результатами, либо зависимыми от полученных финансовых результатов. Временные периоды, в течение которых происходят оттоки и притоки денежных средств, как правило, не являются одномоментными, т.е. всегда существует временной лаг между оттоком и притоком денежных средств. При этом, во-первых, оттоки и притоки денежных средств происходят в соответствии с выбранной технологией и организацией осуществления проекта и заключенными на их основе контрактами; во-вторых, временные периоды между отдельными событиями выполнения определенных этапов проекта не одинаковыми. Рассматриваемые же в отечественной и зарубежной специальной литературе методы дисконтирования ориентируют читателей на упрощенные подходы к оценке денежных потоков без чередования оттоков и притоков в течение одинаковых временных периодов.
Некоторые объяснения этому можно дать исходя из общих принципов учёта, базирующихся на бухгалтерском подходе, а также созданных за последние годы программных продуктов, в основе которых лежит упрощённый моделирующий алгоритм оценки эффективности проектов. Считается, что поступления, генерируемые в рамках одного временного периода могут быть либо в его начале, либо в конце, т. е. они не распределены внутри периода, в течение которого происходят поступления, расположены на одной из его границ. В первом случае поток называют потоком пренумерандо или авансовым, во втором – потоком постнумерандо.
|