Страница 3
Математический аппарат, применяемый в этом случае, достаточно элементарен, дело сводится к вычислениям зависимостей между радиусами сфер, описанных вокруг соответственных правильных многогранников и вписанных в них. Пусть, например, радиус орбиты Земли, а значит и соответствующей сферы, равен 1. Эта сфера описана вокруг икосаэдра, в который вписана сфера Венеры. Решая геометрическую задачу на определение радиуса сферы, вписанной в икосаэдр, и сравнивая полученную величину с радиусом описанной вокруг икосаэдра сферы Кеплер получил соотношение 0,762 : 1. Относительные расстояния до Солнца для шести планет Солнечной системы, полученные Коперником и Кеплером, и современные усредненные значения приводятся в таблице:
|
| Меркурий | Венера | Земля | Марс | Юпитер | Сатурн | |
По Копернику |
0,379 |
0,719 |
1,000 |
1,520 |
5,219 |
9,174 | |
По Кеплеру |
0,419 |
0,762 |
1,000 |
1,440 |
5,261 |
9,163 | |
Современные усредненные значения |
0,387 |
0,723 |
1,000 |
1,524 |
5,203 |
9,539 |
Видим, что данные Кеплера весьма значительно отличаются от вычисленных еще Коперником, и притом во всех случаях — в сторону ухудшения. Объясняя эти расхождения, Кеплер предположил, что каждая из планетных сфер, не будучи материальной, тем не менее имеет некоторую толщину.
Закончив рукопись, Кеплер озаглавил ее так: «Prodromos dissertationem cosmographicum continens Mysterium cosmographicum» — «Предвестник космографических исследований, содержащий космографическую тайну».
Главный поиск. «Новая астрономия»
Над «Новой астрономией» Кеплер работал с небольшими перерывами с 1600 по 1606 г. Значение этой книги состоит прежде всего в том, что в ней дан вывод двух из трех знаменитых законов движения планет, названных его именем. В современной формулировке эти законы обычно звучат так:
I. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.
II. Площади, описываемые радиусами-векторами планет, пропорциональны времени.
Третий закон был опубликован Кеплером позже, в 1619 г., в книге «Harmonices Mundi» («Гармония мира»). Кеплерово сочинение и по форме и по содержанию значительно отличается от многих научных трактатов того времени. Если Коперник, Галилей и Ньютон знакомят нас только с конечными результатами своих научных достижений, то Кеплер совершенно сознательно описывает ход своей работы во всех деталях, включая все неудачи и успехи, ошибки и гениальные догадки, ловушки и их обходы. Почему он так поступает, он объясняет в предисловии: «Для меня важно не просто сообщить читателю, что я должен сказать, но прежде всего ознакомить его с доводами, оговорками, счастливо преодоленными опасностями, которые привели меня к моим открытиям. Когда Христофор Колумб, Магеллан и португальцы, из которых первый открыл Америку, второй Китайский океан, а последние — морской путь вокруг Америки, повествуют, как они сбивались с пути и блуждали в своих путешествиях, мы не только прощаем им это, но, более того, мы не желаем пропуска этих рассказов, так как тогда при чтении было бы потеряно впечатление о всем значительном в их предприятиях. Пусть же поэтому и мне не поставят в вину, когда я, вызывая у читателя интерес, пойду подобным путем в своем изложении. Конечно, при чтении, например похождений аргонавтов, мы сами не принимаем участия в их злоключениях, а трудности и тернии на моем мысленном пути могут задеть и самого читателя, но таков уж жребий всех математических сочинений».
Кеплер начал свое исследование составлением на основании наблюдений Тихо Браге полного списка моментов, долгот и широт для всех противостояний планеты Марс с 1580 г. (Браге наблюдал противостояния Марса десять раз с 1580 по 1600 г., два раза — в 1602 и 1604 гг. их наблюдал Кеплер). Еще Коперник, следуя Птолемею, считал центр земной орбиты истинным центром орбит всех планет. Браге также определял противостояние планеты как положение, противоположное этой точке, т. е. так называемому «среднему Солнцу». Кеплер уже в «Космографической тайне» указывал, что Солнце само является естественным центром планетной системы, и считал, что противостояние следует брать по отношению к реальному, а не к среднему Солнцу. Это было первым существенным нововведением в методы исследования.
Кеплер впервые предположил, что движение планет происходит вследствие воздействия на них некоей силы, исходящей от Солнца. Таким образом, у Кеплера Солнце становится не только источником света и тепла для всей планетной системы, но также и источником движущей планеты силы.
Второе нововведение Кеплера заключалось в следующем. Орбиты всех планет лежат не совсем в одной плоскости — их плоскости образуют одна с другой небольшие углы (например, плоскости орбит Земли и Юпитера составляют угол в 1°18,5'). Если не учесть этот факт, приходится встречаться с большими затруднениями при объяснении некоторых особенностей в наблюдаемых с Земли положениях Марса. Коперник, например, считал, что плоскость орбиты Марса колеблется в пространстве, не интересуясь физической причиной такого странного явления. Предположив, что дело здесь в наличии некоторого постоянного угла между плоскостями планетных орбит, Кеплер без особого труда, по данным наблюдений Браге, убеждается в правильности своей гипотезы и находит угол между плоскостями орбит Земли и Марса равным 1°50'.
Третье нововведение Кеплера более радикально. От Платона и Птолемея до Коперника и Браге астрономы были уверены в том, что планеты совершают свои круговые движения с равномерной скоростью. Кеплер, сохраняя на первых порах движение круговым, отбрасывает аксиому равномерного движения. И при этом он руководствуется прежде всего физическими соображениями: если Солнце управляет движением, является его источником, то его сила должна действовать на планету более интенсивно, когда она находится ближе к источнику, и менее интенсивно, когда планета от него удалится, следовательно, планета будет двигаться с большей или меньшей скоростью в зависимости от ее расстояния до Солнца. Эта идея была не только отрицанием античной традиции, она отвергала и предположение Коперника, по которому не могло быть, « . чтобы простое небесное тело неравномерно двигалось одной сферой . ». Коперник был в свою очередь решительно не согласен с учением Птолемея о том, что планеты движутся равномерно не вокруг центров своих орбит, а вокруг воображаемой точки на некотором расстоянии от центра. Эта точка называлась punctum aequans или aequant (уравнивающей точкой, или эквантом). Коперник, отказавшись от птолемеевых эквантов, ввел вместо них добавочные эпициклы. Кеплер, отбрасывая догму равномерного движения, возвратился к понятию экванта, рассматривая его как важное вычислительное средство.
Этими нововведениями Кеплер несколько облегчил предстоящее решение своей задачи. Кеплер писал: «Ох, сколько я должен был пролить слез над трогательным старанием Апиана, который, следуя Птолемею, зря тратил свое драгоценное время и изобретательность на построение спиралей, петель, винтовых линий, завитков и целого лабиринта инволюций, чтобы изобразить то, что существует только в воображении и которое природа отказывается принять как свое подобие». |
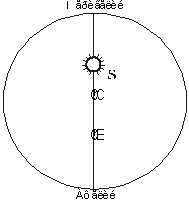
Рис. 3 |
|