Страница 6
Ее издание было предпринято Кеплером за свой счет. Пытаясь хотя бы частично покрыть понесенные расходы, он обращается к своим друзьям с просьбой рекомендовать его книгу заинтересованным лицам и учебным заведениям. О спросе на математическую литературу в то время свидетельствует письмо к Кеплеру Гданьского математика Крюгера, в котором он пишет, что во всей округе видит лишь трех потенциальных покупателей: своего кёнигсбергского коллегу, кёнигсбергскую библиотеку и некоего дворянина по фамилии Невешинский.
Местные власти отнеслись к проделанной Кеплером работе весьма холодно, недвусмысленно дав ему понять, что было бы лучше «эту работу оставить, а довести до конца более важные вещи, такие, как порученные ему «Рудольфинские таблицы» и географическую карту». Однако Кеплер не внял этому весьма категорическому совету и взялся за переделку своей книги, ставя на этот раз целью сделать ее доступной для широких кругов людей, нуждающихся в разработанных им приемах в своей практической деятельности, но не знающих латыни и не разбирающихся в тонкостях математики. С этой целью Кеплер упрощает изложение, меняет последовательность расположения материала, прилагает сведения о системах мер, древних и употреблявшихся в то время, а также таблицы их перевода из одной в другую, но главное — он переводит свое сочинение на немецкий язык. Последнее обстоятельство было очень важным, поскольку научных книг на немецком языке тогда издавалось мало, а математическая терминология почти не была разработана. Поэтому значение появившейся уже весной 1616 г. на книжной ярмарке во Франкфурте книги под названием: «Ausszug auss der uralten Messekunst Archimedis», т. е. «Извлечения из древнего искусства измерения Архимеда .», состоит не только в привлечении внимания к возможностям математических методов широких слоев населения, но и в выполненной здесь большой работе по созданию немецкой математической терминологии. Этим самым, а также изданием нескольких трактатов астрономического содержания на родном языке (и подготовкой нескольких рукописей, оставшихся неизданными) Кеплер внес существенный вклад в развитие языка немецкой естественнонаучной литературы.
Книга «Новая стереометрия» состояла из трех частей. В предисловии Кеплер пишет: «Поскольку . винные бочки связаны с кругом, конусом и цилиндром — фигурами правильными — тем самым они поддаются геометрическим измерениям, принципы которых стоит привести в начале настоящего исследования, как они установлены Архимедом, конечно лишь настолько, насколько этого достаточно для удовлетворения ума, любящего геометрию, а полные и во всех частях строгие доказательства следует искать в самих книгах Архимеда, если кто не убоится тернистого пути их чтения. Впрочем, на некоторых мостах, которые не затронул Архимед, нужно остановиться поподробнее, чтобы и более ученые люди нашли чем воспользоваться и чему порадоваться». Таким образом Кеплер подчеркивает, что в силу практической направленности своего труда он не задерживается на положениях своего великого предшественника, отсылая более требовательных читателей к первоисточникам, но здесь же он говорит и о том, что выходит за пределы достигнутого Архимедом. | 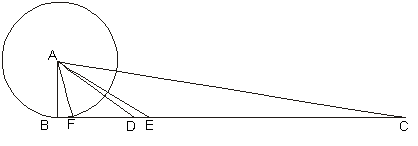
Рис. 6 |
Первая часть сочинения, озаглавленная «Стереометрия правильных кривых тел», в свою очередь состоит из двух частей, в первой из которых — «Архимедовой стереометрии» Кеплер приводит 16 теорем, известных еще Архимеду, но различие в подходе Кеплера и подходе Архимеда к решению соответственных задач становится заметным с самого начала. Остановимся на примере с площадью круга. Произведение Архимеда «Измерение круга» начинается следующим предложением: «Всякий круг равен прямоугольному треугольнику, причем радиус круга равен одной из прилегающих к прямому углу сторон, а периметр — основанию треугольника». Это предложение Архимед доказывает косвенно (методом исчерпывания), показывая с помощью вписанных и описанных правильных многоугольников, что площадь круга будет не больше и не меньше площади указанного треугольника.
Кеплер рассуждает так: «Архимед пользуется косвенным доказательством, приводящим к невозможности, о чем многие и многие писали. Мне же кажется, что смысл этого [доказательства] следующий: окружность круга содержит столько же частей, сколько точек, именно, бесконечное число. Каждую из них рассмотрим как основание некоторого равнобедренного треугольника со стороной АВ, и таким образом в площади круга окажется бесконечное множество треугольников, соединенных вершинами в центре А. Пусть, далее, окружность круга вытянута в прямую, и пусть ей равна ВС, а АВ к ней перпендикулярна (см. Рис. 6). Тогда основания всех этих бесчисленных треугольников, или секторов, будут представляться расположенными друг за другом по прямой ВС; пусть одно из таких оснований будет BF, и какое-нибудь равное ему — DЕ. Соединим точки F, Е, D с А. Таких треугольников ABF, АDЕ над прямой ВС получится столько же, сколько секторов в площади круга, и их основания BF, DЕ и общая высота АВ будут такие же, как у секторов; следовательно, все эти треугольники ABF, АDЕ и т. д. будут равновелики (между собой) и каждый из них будет равновелик соответствующему сектору круга. А значит, и все вместе эти треугольники, имеющие основания на линии ВС, т. е. треугольник ABC, всеми ими составленный, будет равновелик сумме всех секторов круга, т. е. составленной ими площади круга. Это самое и имеет в виду архимедово приведение к нелепости». Архимед действительно мог иметь это в виду. Но учитывая, что между элементарным круговым сектором и элементарным треугольником имеется то различие, что дуга в основании сектора и радиус круга будут при конечном n всегда больше соответственных линий элементарного треугольника, для точности вывода следует показать, что разность между площадями круга и треугольника при увеличении числа делений может стать действительно меньше любого данного сколь угодно малого числа (т. е. что эта разность представляет собой бесконечно малое). Архимед своими рассуждениями это показывает, Кеплер — нет. У Кеплера хорды окружности переходят в точки, каждая из которых продолжает рассматриваться как основание некоторого равнобедренного треугольника. Получается, что площадь круга рассматривается Кеплером как какая-то сумма всех радиусов, а треугольника — как совокупность точек всех прямых, выходящих из одной из его вершин.
Излагая задачи из сочинений Архимеда, Кеплер не пользуется архимедовыми методами доказательств, а применяет суммирование бесконечно большого числа «актуализированных» бесконечно малых. Кеплер говорит, что шар «как бы» содержит бесконечно много конусов, вершины которых лежат в центре, а основания — на поверхности шара, и находит таким образом его объем. Вообще из его неоднократного «как бы» («veluti») видно, что он не стремится дать точное доказательство, а апеллирует только к наглядности. В некоторых местах Кеплер отказывается от доказательств Архимеда, называя их чрезвычайно глубокими, но трудными для понимания, и вместо них приводит рассуждения, которые устанавливают «вероятность» того или другого предложения из соображений индуктивного или интерполяционного характера.
Так Кеплеру удалось преодолеть недостатки метода исчерпывания древних. Ему, разумеется, не было известно содержание архимедового «Послания к Эратосфену», обнаруженного только в 1906 г. Из «Послания» становится ясно, что и Архимед пользовался инфинитезимальньми соображениями, довольно близкими к кеплеровым.
Кеплер, как его современник Кавальери и другие более поздние математики XVII в. (например, Паскаль), часто употреблял выражение «Summa omnium» — «сумма всех» (сумма всех радиусов-векторов, сумма всех ординат), которое выполняло тогда роль нашего термина «интеграл». Кстати, как известно, знак интеграла (удлиненная буква S) был введен Лейбницем в конце XVII в. именно для сокращенной записи выражения «Summa omnium».
|