Развитие оптики, электричества и магнетизма в XVIII веке

Страница 4

Иначе поступил английский ученый Генри Кавендиш (1731 - 1810). Он также исходил из аналогии между силами тягогения и силами электрического взаимодействия. Но он пошел дальше, нежели Эпинус, и проверил на опыте выводы, вытекающие из нее.

Дадим представление об исследовании, выполненном Кавендишем.

Было известно, что если взять полый шар с равномерно распределенной массой, т.е. с постоянной плотностью, то мила тяготения действующая внутри шара на какую-либо массу, будет равна нулю. Это следует из просых соображений. Попытаемся их понять.

Представим себе очень тонкий шаровой слой, образованный двумя очень близкими сферами, имеющими один и тот же центр. Пусть, например, радиус внешней сферы будет R, а толщина слоя d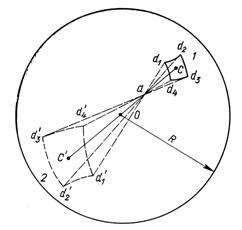. Плотность материала, из которого состоит шаровой слой, r.

Определим силу тяготения, действующую со стороны нашего слоя на материальную точку, помещенную внутри него в какой-то точке а.

Для этой цели проведем через точку а и центр 0 прямую). Эта прямая пересечет внешнюю сферу в двух точках С и С'. Построим теперь на поверхности сферы вокруг точки С очень маленький четырехугольник 1, настолько маленький, что его можно рассматривать как плоский квадрат. Обозначим углы этого квадрата d1, d2, d3,d4. Пусть его площадь S, объем соответствующего элемента шарового слоя V.

Проведем затем прямые линии через точку а и точки d1, d2, d3, d4. Эти прямые пересекут сферу вторично в точках d1', d2', d3', d4'. Соединив эти точки, мы получим второй четырехугольник 2, который также можно будет рассматривать как плоский квадрат. Пусть его площадь будет S', а соответствующий элемент объема шарового слоя будет V'.

Легко видеть, что сила тяготения, действующая на массу m, помещенную в точке a, со стороны элементов шарового слоя V и V', будет равна нулю. Действительно, массы этих элементов будут относиться как площади квадратов S и S'. В свою очередь, площади квадратов S и S' будут прямо пропорциональны квадратам их сторон, следовательно, прямо пропорциональны квадратам расстояний этих элементов до точки а - Са и С'а.

Таким образом, силы тяготения, действующие на массу со стороны элементов 1 и 2, будут прямо пропорциональны квадратам расстояний этих элементов до точки а. Но с другой стороны, эти силы по закону всемирного тяготения должны быть, наоборот, обратно пропорциональны квадратам расстояний этих элементов до точки а.

Учитывая, что силы, действующие со стороны противоположных элементов, имеют противоположные направления, приходим к выводу, что сумма этих сил должна быть равна нулю.

Отсюда сейчас же следует и общий вывод о равенстве нулю силы тяготения, действующей на массу, помещенную внутрь шарового слоя.

Действительно, ведь мы можем весь шаровой слой разбить на маленькие элементы, подобные элементам 1. И для любого элемента всегда найдется другой элемент, действие которого на массу будет прямо противоположным. В результате этого сила тяготения, действующая внутри шарового слоя на массу, будет равна нулю. Таков результат, к которому мы пришли. Нужно только подчеркнуть, что этот результат справедлив для случая, когда сила обратно пропорциональна именно квадрату расстояния. Если бы сила была пропорциональна расстоянию в другой степени, такого результата мы бы не получили.

Полученный вывод мы можем сейчас же перенести на случай электрических сил.

Представим себе опять тонкий шаровой слой, на поверхности которого равномерно распределен электрический заряд. Поместим внутрь этого слоя другой заряд. Если сила взаимодействия между зарядами обратно пропорциональна квадратам расстояний между ними, то по аналогии с п сила, действующая на него со ст по шаровому слою, будет равна нулю. Если поместить внутрь слоя второй такой же заряд того же знака, то они будут отталкиваться друг от друга и двигаться в противоположные стороны.

Кавендиш в 70-х гг. XVIII в. проделал такой опыт. Он взял заряженный металлический шар и поместил его внутрь полого металлического шара, образованного двумя полушариями. Внешний полый шар сначала был не заряжен.

3атем внутренний шар тонкой проволокой соединялся с внешним шаром, для чего было сделано в последнем маленькое отверстие. Через некоторое время полушария разъединяли и освобождали внутренний шар. После этого соединяли его с электроскопом.

Что показывал электроскоп? Если правильно предположение, что силы взаимодействия между зарядами (в данном случае силы оттанкивания) обратно пропорциональны квадрату расстояния между ними, то электроскоп покажет отсутствие заряда.

Действительно, как только внутренний шар соединяли проволокой с полушариями, так сейчас же электричество начинало перетекать с шара по проволоке на полушария, равномерно распределяясь на них. Ведь между зарядами, находящимися на таре, действовала сила отталкивания, но пока шар изолирован, заряды не могли его покинуть. Попав же на внешний шар, заряды равномерно распределялись на его поверхности, и их действие на заряд, находящийся внутри шара, прекращалось.

Перетекание зарядов с внутреннего шара на внешний будет происходить до тех пор,пока они все не покинут внутренний шар. Отсюда Кавендиш и сделал вывод о том, что силы взаимодействия между электрическими зарядами обратно пропорциональны квадрату расстояния между ними.

Таким образом, мы должны сказать, что Кавендиш первым экспериментально установил закон взаимодействия электрических зарядов. Однако он не обнародовал своего открытия. И эта работа оставалась при его жизни неизвестной. О ней узнали гораздо позже, только в середине прошлого столетия, после того как Максвелл опубликовал ее. Конечно, к этому времени она имела уже чисто исторический интерес.

Не зная об исследованиях Кавендиша, французский ученымй Шарль Кунон (1736 - 1806) в 80-х гг. XVIII в. проделал ряд опытов и установил основной закон электростатики, получивший его имя.

Кулон установил, во-первых, что сила взаимодействия между точечными зарядами обратно пропорциональна квадрату расстояния между ними. Эта сила будет силой отталкивания, если заряды одноименные, и силой притяжения, если заряды разноименные.

Во-вторых, Кулон ввел понятие количества электричества и определил, что сила взаимодействия между зарядами пропорциональна их величине.

Кулон также экспериментально исследовал силы взаимодействия между магнитами. На основании данных эксперимента и полагая, что наряду с электрическими существуют и магнитные заряды, Кулон пришел к заключению, что силы взаимодействия между магнитными зарядами или магнитными массами также обратно пропорциональны квадрату расстояния между ними.

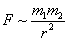В связи с этим закон Кулона для взаимодействия магнитов стали выражать как закон взаимодействия между магнитными массами m1 и m2 в виде формулы:

В последующем, уже в XIX в. выяснилось, что магнитных зарядов не существует. Но законом Кулона для магнитов продолжали пользоваться, хотя ему уже придавали иной смысл, нежели тот, который вкладывал в него Кулон.

Введение понятия потенциалав электростатику

Открытие закона Кулона было очень важным шагом в развитии учения об электричестве и магнетизме. Это был первый физический закон, выражающий количественные соотношения между физическими величинами в учении об электричестве и магнетизме.

С помощью этого закона можно было решать задачи о нахождении сил, действующих на заряды со стороны других зарядов, как угодно расположенных в пространстве. Если это были точечные заряды, то подобные задачи решались сразу непосредственным применением закона Кулона. Если же заряды распределялись в телах непрерывно по объему или по поверхности, то нужно было ввести понятие объемной или поверхностной плотности зарядов. Именно когда заряды непрерывно распределялись по объему, то плотность заряда r определялась величиной Dq/DV, где DV - элемент объема, а Dq - заряд, находящийся в этом объеме, совсем так же, как определяется плотность вещества в случае неравномерного распределения масс в теле.