Методы решения уравнений в странах древнего мира
Методы решения уравнений в странах древнего мира
История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.
В Древнем Египте и Вавилоне использовался метод ложного положения («фальфивое правило»)
Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь == с, в котором а, Ь, с — целые числа. По правилам арифметических действий ах = с — b,
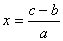
Если Ь > с, то с — b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).
Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения.
В папирусе Ахмеса 15 задач решается этим методом. Решение первой из них позволяет понять, как рассуждал автор.
Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали «хау» и переводили словом «куча» («куча» или «неизвестное количество» единиц). Теперь читают немного менее неточно: «ага».
bqt задача № 24 сборника Ахмеса:
«Куча. Ее седьмая часть ('подразумевается: «дают в сумме») 19. Найти кучу».
Запись задачи нашими знаками:
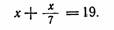
Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:
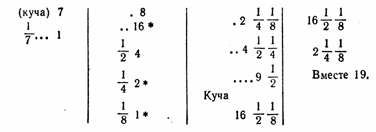
Во многих задачах в начале или в конце встречаются слова: «Делай как делается», другими словами: «Делай, как люди делают».
Смысл решения Ахмеса легко понять.
Делается предположение, что. куча есть 7; тогда 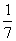 ее часть есть 1. Это записано в первом столбце.
ее часть есть 1. Это записано в первом столбце.
Во втором столбце записано, что при предположении х=7 куча и ее 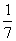 часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит
часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит 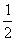 от 8, получает 4. Так как это больше нехватки 3, то на
от 8, получает 4. Так как это больше нехватки 3, то на 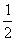 предположение умножить нельзя. Но
предположение умножить нельзя. Но 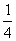 от 8 есть 2,
от 8 есть 2, 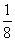 от восьми 1. Ахмес видит, что
от восьми 1. Ахмес видит, что 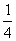 и
и 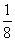 первоначального результата дают точно те 3 единицы, которых не хватало. Отметив
первоначального результата дают точно те 3 единицы, которых не хватало. Отметив 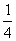 и
и 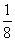 значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на
значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на 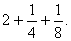
Умножение числа 7 на смешанное число 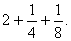 Ахмес заменяет умножением смешанного числа
Ахмес заменяет умножением смешанного числа 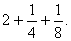 на 7. В третьем столбце выписаны:
на 7. В третьем столбце выписаны: 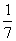 часть искомой кучи есть
часть искомой кучи есть 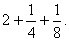 , удвоенное это число:
, удвоенное это число: 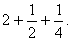 и учетверенное:
и учетверенное: 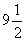 . Сумма этих трех чисел, равная числу
. Сумма этих трех чисел, равная числу 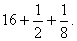 , есть произведение первоначального предположения 7 на
, есть произведение первоначального предположения 7 на 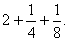 .
.
Итак, куча равна 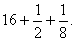 .
.
В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи 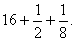 и его
и его 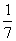 части
части 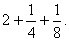 . В сумме получается 19, и решение заканчивается обычным для автора заключением: «Будет хорошо».
. В сумме получается 19, и решение заканчивается обычным для автора заключением: «Будет хорошо».
Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах == b. Его применяли как египтяне, так и вавилоняне.
У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получил ту форму, в которой он перешел в учебники европейских народов, в том числе в «Арифметику» Магницкого. Магницкий называет способ решения «фальшивым правилом» и пишет о части своей книги, излагающей этот метод:
Зело бо хитра есть сия часть,
Яко можеши ею все класть (вычислить. — И. Д.)
Не токмо что есть во гражданстве,
Но и высших наук в пространстве,
Яже числятся в сфере неба,
Якоже мудрым есть потреба.
Содержание стихов Магницкого можно вкратце передать так: эта часть арифметики весьма хитрая. При помощи ее можно вычислить не только то, что понадобится в житейской практике, но она решает и вопросы «высшие», которые встают перед «мудрыми».
Магницкий пользуется «фальшивым правилом» в форме, какую ему придали арабы, называя его «арифметикой двух ошибок» или «методой весов».
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
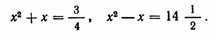
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
. Как составлял и решал Диофант квадратные уравнения ,
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
«Найти два числа, зная, что их сумма равна 20, а произведение — 96».
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение
(1)