Страница 2
В зависимости от характера изменения погрешности измерений различают систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерений одной и той же величины в одних и тех же условиях, и случайные погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины.
5Систематические погрешности
Наличие систематических погрешностей устойчиво искажает результаты измерений, а отсутствие или близость их к нулю определяет правильность измерений. Систематические погрешности классифицируются в зависимости от причин возникновения и по характеру проявления в процессе измерений.
Методическая погрешность - составляющая погрешности измерения, происходящая от несовершенства метода измерений.
Инструментальная (аппаратурная) погрешность измерения зависит от погрешностей применяемых средств измерений.
Внешние погрешности обусловлены внешними по отношению к прибору влияниями,то есть условиями, при которых проходят измерения.
Субъективные погрешности - составляющие погрешности из-мерения, обусловленные индивидуальными особенностями оператора.
Задача обеспечения правильности измерений должна предусматривать обнаружение, оценку и уменьшение (либо полное исключение) систематических погрешностей. Рассмотрим наиболее широко применяемые в практике способы обнаружения, оценки и уменьшения систематических погрешностей. Для этого рекомендуется тщательно устанавливать нулевое показание и калибровать средство измерения, прогревать его в течение времени, указанного в инструкция по эксплуатации, применять при сборке короткие соединительные провода, а на высоких частотах - коаксиальные кабели, заземлять, в необходимых случаях экранировать, правильно размещать средство измерения (устанавливать в рабочее положение, размещать вдали от источников тепла и электромагнитных полей ), применять только прверенные измерительные приборы,
В процессе измерений систематические погрешности могут быть исключены с помощью одного из следующих способов. Вопрос5: Способы исключения систематических погрешностей
Способ замещения, при котором измеряемый объект заменяется образцовой мерой, находящейся в тех же условиях, что и сам объект.
Способ компенсации по знаку, при котором измерение проводят дважды так, чтобы не известная но абсолютному значению, но известная по своей природе систематическая погрешность входила в результаты наблюдений с противоположными знаками. Тогда полусумма их результатов будет свободна от этой погрешности.
Способ симметричных наблюдений, который оказывается весьма эффективным при исключении прогрессивной погрешности, являющейся линейной функцией соответствующего аргумента. Измерения проводят последовательно через одинаковые интервалы изменения аргумента, а обработку полученных результатов осуществляют с учетом равенства среднего значения погрешности любой нары симметричных наблюдений погрешности, соответствующей средней точке данного интервала.
Способ рандомизации (перевод систематической погрешности в случайную). Пусть, например, имеется n однотипных приборов с систематической погрешностью одинакового происхождения. Если для данного прибора эта погрешность постоянна, то от прибора к прибору она изменяется случайным образом. Поэтому измерение одной и той же величины всеми приборами и усреднение результатов полученных наблюдений позволяет значительно уменьшить эту погрешность.
После проведения измерений при обработке результатов систематические погрешности могут быть уменьшены за счет введения поправочных слагаемых (q ) и поправочных множителей: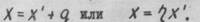
Величины q и j определяются по результатам предварительных испытаний, на основании которых строятся поправочные таблицы и графики в зависимости q и j от условий проведения эксперимента.
Вопрос 6:Сущность вероятностного описания случайных погрешностей
6. Случайные погрешности I
Из-за влияния многочисленных и принципиально неустранимых факторов, обусловливающих случайные погрешности, результат каждого измерения Аj будет отличаться от истинного значения X измеряемой величины: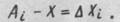
Эту разность называют случайной погрешностью отдельного измерения. Истинное значение X нам неизвестно. Однако, проведя большое количество измерений исследуемой величины X, можно выявить следующие статистические закономерности:
1. Если провести серию измерений исследуемой величины и определить среднее значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине.
2. Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений.
Эти статистические закономерности справедливы лишь при многократном повторении измерений. После обработки результатов измерений получается не абсолютно достоверный, а наиболее вероятный результат им будет среднее арифметическое значение
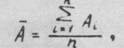
где n - число измерений.
Вопрос 7:Сущность точечного описания измеряемой величины при многократных прямых измерениях.
7.Эти статистические закономерности справедливы лишь при многократном повторении измерений. После обработки результатов измерений получается не абсолютно достоверный, а наиболее вероятный результат им будет среднее арифметическое значение
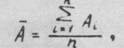
где n - число измерений.
Указанные статистические закономерности большого числа измерений позволяют поставить вопрос о законе, по которому происходит распределение случайных погрешностей. В практике электрорадиоизмерений наиболее распространенным является нормальный или гауссовский закон распределения:
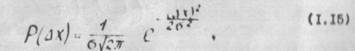
p(DХ) - плотность вероятности случайной погрешности DХ=А-Х и но своему смыслу равны отношении вероятности попадания случайной величины внутрь интервала DХ и длине этого интервала в предположении, что последний стремится к нулю;
б - среднее квадратическое отклонение случайной погрешности.
Среднее квадратическое отклонение случайной погрешности определяют из соотношения:
где Aj - численный результат отдельного измерения:
Б=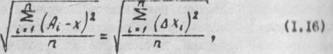
n - число измерений.
Характер кривых, описываемых (1.15), показан на рис. 1.3а для грех значений б. Как видно из рис. 1.3а, чем меньшой, тем уже кривая, и, следовательно, том реже встречаются большие отклонения.
Вопрос 8: Сущность интервального оценивания результатов многократныхпрямых измерений
8. На практике (особенно при малом значении n ) необходимо оценить точность и надежность полученных результатов для среднего значения и среднего квадратического отклонения. Для этой цели пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью понимают вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интервалом, а характеризующую его вероятность - доверительной вероятностью. Яри гауссовском законе распределения значения доверительных интервалом сведены в таблицы интеграла вероятности. Определение доверительных интервалов с использованием соотношений 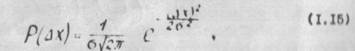 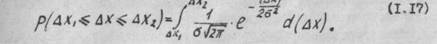 справедливо лишь при числе измерений (n> 20 .30) На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерений, Применение формулы (1.17) в этом случае дает заниженное значение доверительного интервала, то есть оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнить доверительный интервал можно с помощью коэффициентов Стьюдента tn , которые зависят от задаваемой доверительной вероятности p и числа измерений n. Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат можно записать так: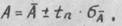
|