Контрольная работа №1
Вариант №5
Задание №1
Найти
матрицу АВ+3Е и ВА+3Е, где
 ,
, 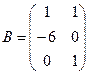 ,
,
Е
– единичная матрица соответствующего порядка.
Решение:
Найти
матрицу АВ+3Е
1.1 Найдем размер матрицы произведения:
А * В = С
2*3 3*2
2*2
1.2 Вычисляем элементы матрицы произведения А*В:
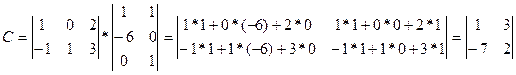

1.3 Вычислим 3Е:

1.4 Находим матрицу АВ+3Е:

Ответ:

Найти
матрицу ВА+3Е:
1.1 Найдем размер матрицы произведения:
В *
А = С
3*2
2*3 3*3
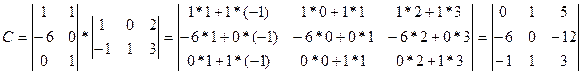
1.2 Вычислим матрицу 3Е:
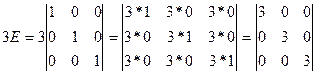
1.3 Найдем матрицу В*А+3Е
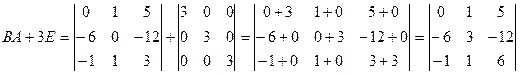
Ответ:
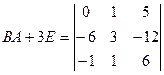 .
.
Задание №2
Найти
предел:

Решение:
Имеем
неопределенность вида  применим правило Лопиталя
применим правило Лопиталя
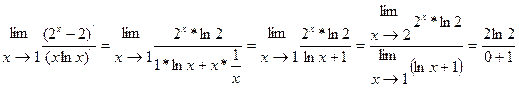
Ответ:
 =2ln2.
=2ln2.
Задание №3
Найти
произвольную функции:

Решение:
Находим
производную по формуле сложной функции 
 +
+
Находим
производные


по
сколько  и
и  - производные от
постоянной величины равны нулю.
- производные от
постоянной величины равны нулю.
 +
+
Упростим
полученное выражение и заменим  по определению логарифмов.
по определению логарифмов.
 =
=
Ответ:

Задание №4
Из
квадратного листа жести, длина стороны которого 54 см, вырезают по углам
одинаковые квадраты и из оставшейся части склеивают открытую коробку. Какова
должна быть длина стороны вырезаемых квадратов, чтобы вместимость коробки была
наибольшей?
Решение:
Возьмем
за x длину стороны вырезанного квадрата, за а длину
стороны квадратного листа жести. Получается, что x – высота коробки,
а дно коробки имеет квадрат со стороной a-2x тогда объем коробки
 формула
формула  имеет область
определения 0<x<
имеет область
определения 0<x<
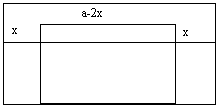
Найдем
производную 
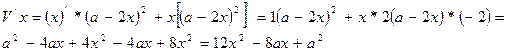
Находим
критические точки функции в которых они имеют максимальное значение т.е.  =0,
=0,

Находим
значение корней  и
и 



Корень
 находится вне
определения функции тогда принимаем
находится вне
определения функции тогда принимаем  .
.
При
α=54см  =9см.
=9см.
Ответ:
Длина стороны вырезаемого квадрата равна 9см.
Задание №5
Составить
уравнения касательных к гиперболе  , которые перпендикулярны прямой x+y-4=0. Сделать
чертеж.
, которые перпендикулярны прямой x+y-4=0. Сделать
чертеж.
Решение:
Преобразуем
формулу прямой x+y-4=0 к виду уравнения прямой с угловым
коэффициентом y=kx+b
y=-x+4.
Следовательно,
угловой коэффициент прямой y=-x+4 равен  .
.
Угловые
коэффициенты прямых касательных к гиперболе, представленной формулой  , будут выражаться производной
, будут выражаться производной  :
:
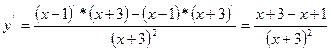 ;
;
 т.е.
т.е.  .
.
Из
условия перпендикулярности прямых  ,
,  .
.
Подставляем
 в формулу
касательных
в формулу
касательных  находим
находим 





т.е.
имеем две касательные прямые.
Находим
уравнения касательных к гиперболе  по формуле
по формуле

 для
для 


 для
для 


Ответ:
Разрешив задачу получим две касательных уравнения которых  и
и  .
.
Рассматриваемая
гипербола есть дробно-линейная функция вида  .
.
В
данной задаче гипербола дана формулой  из этого следует
из этого следует  : b=-1; c=1; d=3.
: b=-1; c=1; d=3.
m определится формулой 

При
m<0 ветви гиперболы расположены во 2 и 4 квадрантах.
В
новой системе координат центр  определится по
формулам
определится по
формулам  и
и  подставляя данные
подставляя данные  , с=1, d=3 получим
, с=1, d=3 получим  ;
;  ;
;  .
.
Координаты
вершины гиперболы определяются формулам
 при m=4
при m=4
 .
.
Так
как ветви гиперболы находятся во 2 и 4 квадрантах, то координата вершины ветви
гиперболы во 2 квадранте имеет координаты в новой системе координат  ,
,  . Для вершины ветви в 4 квадранте
. Для вершины ветви в 4 квадранте  ,
,  .
.
Для
выполнения чертежа имеем уравнения прямых
y=-x+4


Координаты
 центра новой системы
координат
центра новой системы
координат  , координаты вершин ветвей гиперболы в новой системе
координат
, координаты вершин ветвей гиперболы в новой системе
координат  ;
;  .
.
Задание №6
Исследовать
функцию  и схематично построить
ее график.
и схематично построить
ее график.
Решение:
1) Область определения функции:
Область
определения функции – вся числовая ось -∞<x<+∞ при x=0 и y=0.
2) Функция нечетная, так как





3)
Вертикальных асимптот функция не имеет, так как
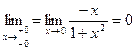 и не имеет разрыва в
точке х=0 потому что y(0)=0.
и не имеет разрыва в
точке х=0 потому что y(0)=0.
4)
Поведение функции в бесконечности:
Находим
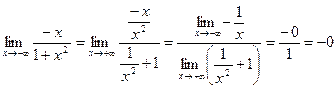

аналогично
делая преобразования получим  . Анализируя полученные результаты заключаем, что справа от
х=0 в бесконечность
. Анализируя полученные результаты заключаем, что справа от
х=0 в бесконечность  предел y(x) стремится к
(-0), слева от х=0
предел y(x) стремится к
(-0), слева от х=0  предел y(x) стремится к
(+0). Иными словами ось абцисс является горизонтальной асимптотой.
предел y(x) стремится к
(+0). Иными словами ось абцисс является горизонтальной асимптотой.
5)
Экстремум функции определяется по первой производной по формуле  ;
;
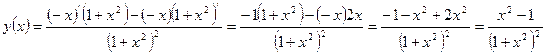 приравниваем
приравниваем  то есть
то есть 

 . Получаем две точки экстремума в точках
. Получаем две точки экстремума в точках  и
и  .
.
На
основании пункта 4 решения задачи заключаем:
Справа от точек - функция
функция  y(x) монотонно
убывает стремясь к (-0).
y(x) монотонно
убывает стремясь к (-0).
Слева
от точек  функция
функция  y(x) монотонно
убывает стремясь к (+0) точнее в интервале
y(x) монотонно
убывает стремясь к (+0) точнее в интервале  функция убывает
функция убывает  в интервале
в интервале  функция убывает
функция убывает  .
.
6)
Характер выпуклости определяем по второй производной:
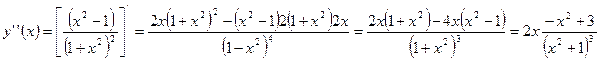 .
.
Вычисляем
 в критических точках
в критических точках  и
и 
 функция выпуклая вниз,
функция выпуклая вниз,
 функция выпуклая
вверх.
функция выпуклая
вверх.
7)
В интервале (1;-1) функция меняет свое значение от – к + и пересекает ось абцисс
в точке х=0 ибо значение функции в этой точке y(0)=0. В точке х=1 значение функции y(1)= .
.
В
точке х=-1 значение функции y(-1)= .
.
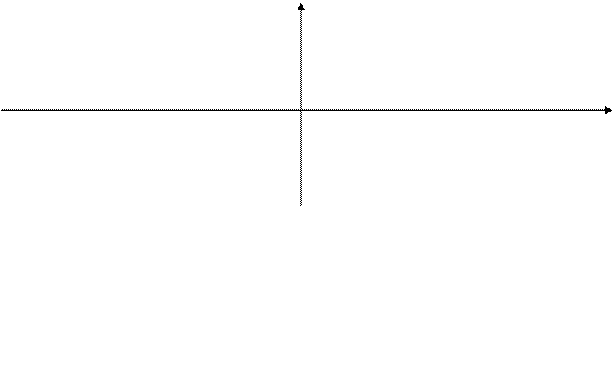
На
основании изложенного строим график:
Контрольная работа №2
Задание №1
Найти неопределенные
интегралы:
1)
2) 
Решение:
Для нахождения интеграла  применяем метод замены
переменной.
применяем метод замены
переменной.
Получим  тогда
тогда 
 найденные значения
подставляем в интеграл
найденные значения
подставляем в интеграл
 возвращаемся к х
возвращаемся к х 
Ответ:  .
.
Задание №2
Найти неопределенные
интегралы:

Решение:
Для нахождения интеграла  воспользуемся методом
интегрирования по частям.
воспользуемся методом
интегрирования по частям.
Получим u=(2-x) dv= находим du=-dx
находим du=-dx
 .
.
По формуле интегрирования по
частям  получаем
получаем 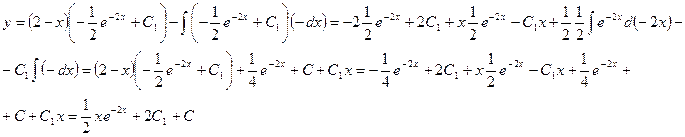 Ответ: искомый интеграл равен
Ответ: искомый интеграл равен  .
.
Задание №3
Вычислить определенные
интегралы:

Решение:
Для вычисления интеграла y= применим замену
переменной.
применим замену
переменной.
Примем  и dx=2t*dt. Если х=4, то t=2, если х=9, то t=3.
и dx=2t*dt. Если х=4, то t=2, если х=9, то t=3.
После замены переменной
получаем 
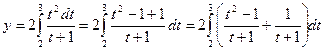

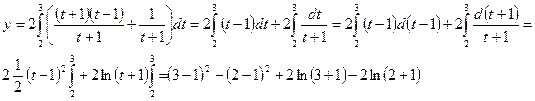

Ответ:  =
=
Задание №4
Вычислить определенные
интегралы:

Решение:
 представим
представим  тогда
тогда


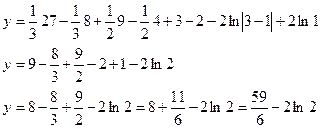
Ответ:
 =
= .
.
Задание №5
Вычислить объем тела, образованного вращением вокруг
оси Oy фигуры,
ограниченной линиями:
 .
.
Решение:
Для схематического построения фигуры ограниченной
указанными линиями проведем анализ графиков  .
.
Кривая  является параболой с вершиной в начале координат,
симметричной относительно оси ординат.
является параболой с вершиной в начале координат,
симметричной относительно оси ординат.
 - так же парабола координату х вершины кривой
- так же парабола координату х вершины кривой  найдем из уравнения
найдем из уравнения  , 4-2х=0,
, 4-2х=0,  . Ордината вершины
определяется из
. Ордината вершины
определяется из  ,
,  ,
,  координаты вершины
А(2;4).
координаты вершины
А(2;4).
Точки пересечения кривой  с осью х определяется
из о=4х-
с осью х определяется
из о=4х- .
.
Две точки х=0 и х=4 то есть О(0;0) и B(4;0).
Общие точки пересечения кривых определяется из
совместного решения уравнений  ,
,  ,
,
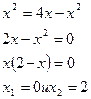
Таким образом, пересечение линий  и
и  происходит в начале
координат и в вершине параболы
происходит в начале
координат и в вершине параболы  в точке А(2;4).
в точке А(2;4).
Из построенного графика определяем, что объем тела
образуется вращением плоской фигуры вокруг оси Oy ограниченной с низу осью х справа кривой  от точек А до В , слева линией
от точек А до В , слева линией  от точки А до точки О
то есть плоской фигуры ОАВ.
от точки А до точки О
то есть плоской фигуры ОАВ.
Задание №6
Пользуясь разложением подынтегральной функции в ряд
Маклорена, вычислить интеграл 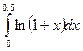 с точностью до 0,001. Вычислить
этот же интеграл, используя формулу Ньютона-Лейбница.
с точностью до 0,001. Вычислить
этот же интеграл, используя формулу Ньютона-Лейбница.
Сравнить полученные результаты.
Решение:
Ряд Маклорена представлен формулой:

В данном случае f(x)=ln(1+x).
При x=0 функция f(0)=ln(1+0), f(0)=ln1, а ln1=0 получаем f(0)=0.
Находим производные от функции f(x)=ln(1+x) и определяем
их значения при x=0,
 ,
,


 ,
,
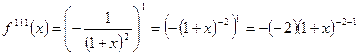 ,
,

 ,
,
 при х=0,
при х=0,
 ,
,
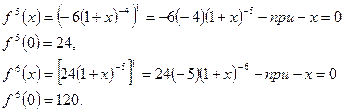
Для ясности выпишем значения производных при х=0
значение f(0)^
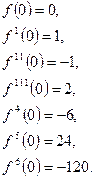
Эти значения подставим в формулу ряда Маклорена:
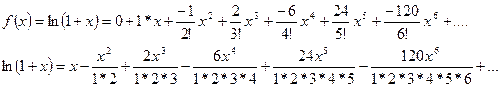
Окончательно получаем разложение функции ln(1+x) так как
остальные члены разложения от n и далее n+1 отброшены:

Вычисляем интеграл:
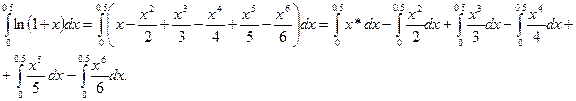
Вычислим каждый интеграл по отдельности:
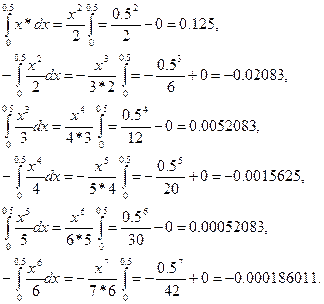
Заменим результаты вычисления вряд:
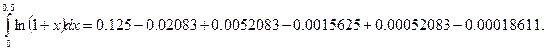
По условию задачи погрешность задана  .
.
Для достижения заданной погрешности последние члены
суммы ряда можно отбросить и первый отброшенный член ряда с которого
отбрасываются все последующие остальные, будет пятый (ибо погрешность не
превышает абсолютной величины первого отброшенного члена).
0,00052083<0.001
Окончательно
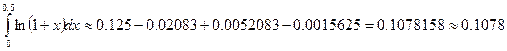 ,
,
а)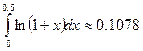 .
.
Вычисляем этот же интеграл другим способом без
разложения вряд по формуле Ньютона-Лейбница.
Дано 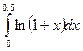 .
.
Решение:
Применяем интегрирования по частям.
Пусть  тогда
тогда  v=x.
v=x.
Применим формулу по частям получаем
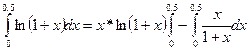 .
.
Для нахождения интеграла 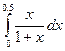 делаем подстановку 1+x=t тогда dx=dt, x=t-1 .
делаем подстановку 1+x=t тогда dx=dt, x=t-1 .
Находим новые пределы интегрирования: если х=0, то t=1; если х=0,5, то t=1.5
 .
.
Вычислим  определяем значение
интеграла
определяем значение
интеграла 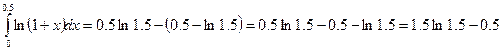
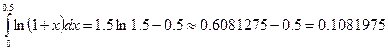
б)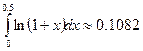 с заданной
погрешностью сравнивая результаты вычислений интегралов а и б получим
0,1082-0,1078=0,0004.
с заданной
погрешностью сравнивая результаты вычислений интегралов а и б получим
0,1082-0,1078=0,0004.
Ответ: При вычислении интеграла 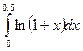 методом приближенных
вычислений получаем результат с данной точностью: y=0,1078.
методом приближенных
вычислений получаем результат с данной точностью: y=0,1078.
При вычислении интеграла по формуле Ньютона-Лейбница
получаем результат y=0,1082.
Расхождения составляет  .
.
Точный без погрешностей результат 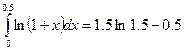 .
.