8. В партии из 8 телевизоров половина не настроены. Наудачу отобраны три телевизора. Какова вероятность того, что в число отобранных попадет хотя бы один не настроенный?

Решение:

Введем событие 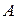- в число настроенных телевизоров попадет хотя бы один настроенный. Хотя бы один означает, что в это число попадет один, два или три настроенных телевизора.

Рассмотрим противоположное событие 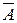- в число отобранных попали все ненастроенные телевизоры. Тогда по формуле классической вероятности:

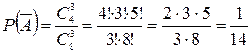
Тогда вероятность события А равна:

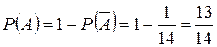
Ответ: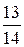

17. Оптовая база снабжает товаром n = 15 магазинов. Вероятность того, что в течении дня поступит заявка на товар, равна p = 0.3 для каждого магазина. Найти вероятность того, что в течении дня: а) поступит 3 заявки; б) поступит не менее 5 и не более 12 заявок; в) поступит хотя бы одна заявка. Каково наивероятнейшее число поступающих в течении дня заявок и чему равна соответствующая ему вероятность?

Решение:

а) Искомую вероятность найдем по формуле Бернулли:

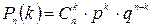, где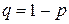

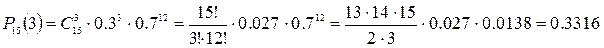б) Далее будем использовать интегральную теорему Муавра – Лапласа:

 

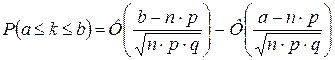
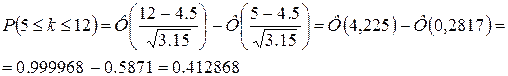
Значения функций Лапласа найдем из таблицы.

в) Найдем вероятность того, что не поступило ни одной заявки:

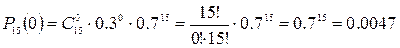
Тогда вероятность того, что поступила хотя бы одна заявка равна:

 

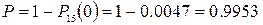
Наивероятнейшее число 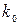 заявок найдем по формуле:

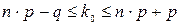
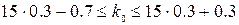
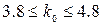
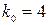
Соответствующая ему вероятность равна:

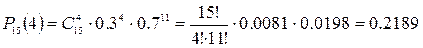
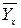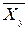68. По данным корреляционной таблицы найти условные средние и . Оценить тесноту линейной связи признаками X и Y и составить уравнения линейной регрессии Y по X и X по Y. Сделать чертеж, нанеся на него условные средние  и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.

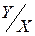
	15	20	25	30	35	45
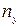
25	4	2					6
35		6	4				10
45			6	45	2		53
55			2	8	6		16
65				4	7	4	15
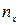
	4	8	12	57	15	4

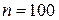
Решение:

Найдем условные средние 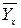 и 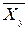по формулам:

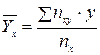 и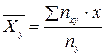

  

 

  

 

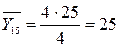
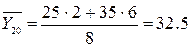
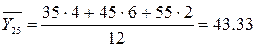
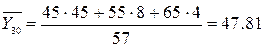
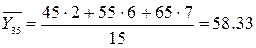
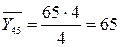
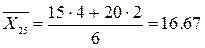
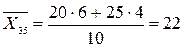
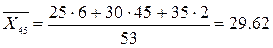
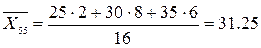
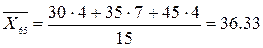
Для того, чтобы найти коэффициент корреляции составим вспомогательные таблицы:

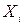
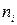
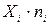
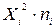
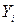
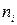
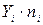
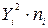
15	4	60	900		25	6	150	3750
20	8	160	3200		35	10	350	12250
25	12	300	750		45	53	2385	107325
30	57	1710	51300		55	16	880	48400
35	15	525	18375		65	15	975	63375
45	4	180	8100			100	4740	235100
	100	2935	82625

Найдем выборочные средние:

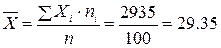
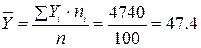
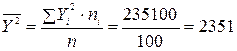
Найдем средние квадратические отклонения:

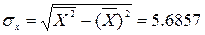
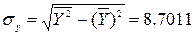
Найдем вспомогательную величину:

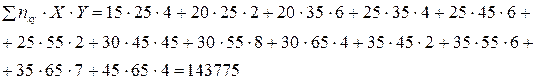
Найдем коэффициент корреляции:

,

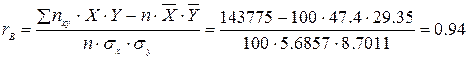следовательно связь между признаками X и Y является тесной.

Составим уравнение линии регрессии 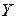по: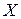

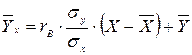
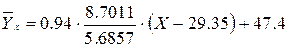
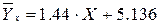
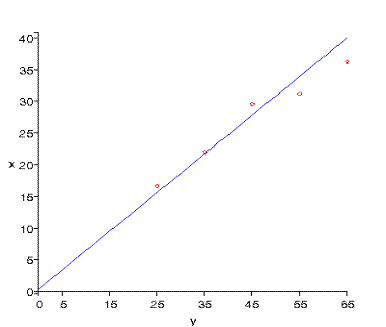
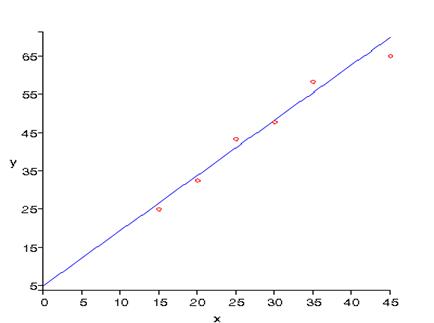
Построим график линии регрессии и нанесем точки :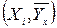

Составим уравнение линии регрессии 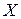по :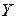

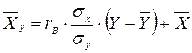
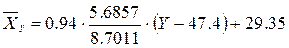
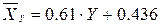
Построим график линии регрессии и нанесем точки 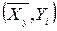: