МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. Туполева
ФИЛИАЛ «ВОСТОК»
Расчетно-графическая работа
по дисциплине
«Разработка производственных и управленческих решений»
Вариант 17
Выполнил: ст. гр. 21404
Овчинникова О.В.
Проверил: Гашева М.В.
Чистополь 2009
Решение задачи симплексным методом
Симплекс метод- это метод упорядочивания перебора опорных планов, упорядочивание в данном случае обеспечение последовательным перебором опорных планов с монотонным изменением значения целевой функции в сторону возрастания(убывания).
Исходные данные:
Предприятие занимается производством 2 видов продукции 1 и 2, для их производства требуется 3 вида сырья. На изготовление единицы изделия 1 требуется сырья каждого вида  кг, а для изделия 2- кг, а для изделия 2-  кг. Стоимость единицы изделия 1 - кг. Стоимость единицы изделия 1 - , а для 2- , а для 2-  т.р. Необходимо составить такой план производства изделий, при котором прибыль от производства и реализации данной продукции будет максимальной. На предприятии имеется сырья в количестве т.р. Необходимо составить такой план производства изделий, при котором прибыль от производства и реализации данной продукции будет максимальной. На предприятии имеется сырья в количестве  . .
 |
 |
 |
 |
 |
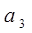 |
 |
 |
 |
 |
 |
| 606 |
802 |
840 |
9 |
15 |
15 |
27 |
15 |
3 |
5 |
6 |
Решение:
Составим экономико-математическую модель задачи. Для этого обозначим  - количество изделий А. - количество изделий А.  - количество изделий В. Эта задача является задачей оптимального использования сырья, поэтому система организации имеет вид: - количество изделий В. Эта задача является задачей оптимального использования сырья, поэтому система организации имеет вид:
  + +  ≤606 ≤606
  9 9 +27 +27 ≤606 ≤606
15 +15 +15 ≤802 (1) ≤802 (1)
15 +3 +3 ≤840 ≤840
Где справа стоит количество каждого вида сырья, которые не может быть превышено в процессе производства изделий.
 ≥0, ≥0,  ≥0 (2) ≥0 (2)
Целевая функция представляет собой общую стоимость произведенной продукции.
С=5 +6х2
=> макс. (3) +6х2
=> макс. (3)
Для решения задач симплекс методом приводят ее к каноническому виду, введя дополнительные балансовые переменные х3
,х4
,х5
, которые означают остатки сырья соответственно 1,2, 3 типов, при этом неравенство преобразуется в уравнение, т.е. левая часть сбалансирована с правой.
9 +27 +27 + х3
≤606 + х3
≤606
15 +15 +15 + х4
≤802 (4) + х4
≤802 (4)
15 +3 +3 +х5
≤840 +х5
≤840
х3
, х4
, х5
- остатки 1,2,3 вида сырья.
х1
,х2,
х3
,х4,
х5
≥ 0 (5)
С=5 +6х2
+0х3
+0х4
+0х5
=> макс. (6) +6х2
+0х3
+0х4
+0х5
=> макс. (6)
Систему (4) можно записать в другом виде:
р1
х1
+р2
х2
+р3
х3
+р4
х4
+р5
х5
=р0
р1 р2
р2 р3
р3 р4
р4 р5
р5 р0
р0
Здесь векторы р3
р4
р5
имеют предпочтительный вид, т.е являются единичными в одном из компонентов и нулевыми во всех остальных компонентах. Р0
- называется столбцом свободных членов системы ограничений, для решения системы (4)-(6) симплекс методом необходимо иметь опорный план, т.е. допускаются решения системы (4), для этого надо разделить на 2 группы- базисные и свободные. Сначала выбираем базисные, в качестве их выбирают векторы, имеющие предпочтительный вид, т.е в данном случае р3
р4
р5.
им соответствуют базисные переменные х3
, х4
, х5
системы (4). Остальные переменные х1
,х2
- будут свободными, при получении базисного решения все свободные переменные =0. Подставив в (4) х1
=х2
=0, получаем остальные компоненты опорного плана х3
=606, х4
=802,х5
=840. В векторном виде этот опорный план выглядит так: х0
=(0,0,606,802,840). Подставив компоненты х0
в целевую функцию (6) получаем значение целевой функции=0. С (х0
)=0.
1 симплексная таблица( опорный план в виде симплекс таблицы)
| Оценка базисных переменных |
Базисные переменные |
Свободные члены |
5 |
6 |
0 |
0 |
0 |
| С
|
Х |
Р0
|
Р1
|
Р2
|
Р3
|
Р4
|
Р5
|
| 0 |
Х3
|
606 |
9 |
27 |
1 |
0 |
0 |
| 0 |
Х4
|
802 |
15 |
15 |
0 |
1 |
0 |
| 0 |
Х5
|
840 |
15 |
3 |
0 |
0 |
1 |
| С |
0 |
-5 |
-6 |
0 |
0 |
0 |
Переход к новому опорному плану, выбор разрешающего столбца:
СК
=мин{Сj
(cj
|
<0)}=мин {-5; -6 }=-6=С2
=К=2
Выбор разрешающей строки:
bl
/ alk
=min {bi
/ai2
(ai2
>0)} min{606/27;802/15;840/3}={22;53;280} =22=b1
/a12
=l=1
Генеральный элемент: alk
=а12
=27
Переход к новой симплексной таблице:
B1
= b1
/ а12
=606/27=22
c=C-ck
bс
=c-c2
b1
=0-(-6)*22=132
alj
=alj
/alk
 9/27=1/3 9/27=1/3
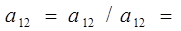 27/27=1 27/27=1
 =1/27 =1/27
 =0/27=0 =0/27=0
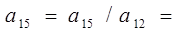 0/27=0 0/27=0

 -5-(-6)*1/3=-3 -5-(-6)*1/3=-3
 -6-(-6)*1=0 -6-(-6)*1=0
 0-(-6)*1/27=2/9 0-(-6)*1/27=2/9
 0-(-6)*0=0 0-(-6)*0=0
 0-(-6)*0=0 0-(-6)*0=0

 =802-15*22=472 =802-15*22=472
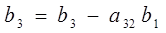 =840-3*22=774 =840-3*22=774

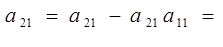 15-15*1/3=10 15-15*1/3=10
 15-15*1=0 15-15*1=0
 0-0*1/27=0 0-0*1/27=0
 1-1*0=1 1-1*0=1
 0-0*0=0 0-0*0=0
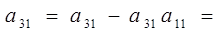 15-15*1/3=10 15-15*1/3=10
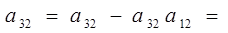 3-3*1=0 3-3*1=0
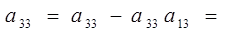 0-0*1/27=0 0-0*1/27=0
 0-0*0=0 0-0*0=0
 1-1*0=1 1-1*0=1
Вторая симплексная таблица
| Оценка базисных переменных |
Базисные переменные |
Свободные члены |
5 |
6 |
0 |
0 |
0 |
| С
|
Х |
Р0
|
Р1
|
Р2
|
Р3
|
Р4
|
Р5
|
| 6 |
Х2
|
22 |
1/3 |
1 |
1/27 |
0 |
0 |
| 0 |
Х4
|
472 |
10 |
0 |
0 |
1 |
0 |
| 0 |
Х5
|
774 |
10 |
0 |
0 |
0 |
1 |
| С |
132 |
-3 |
0 |
-2/9 |
0 |
0 |
Переход к новому опорному плану, выбор разрешающего столбца:
СК
=мин{Сj
(cj
|
<0)}=мин {-3; 0}=--3=С1
=К=1
Выбор разрешающей строки:
bl
/ alk
=min {bi
/ai
1
(ai
1
>0)}min{22/1/3;472/10;774/10}={66;47;77}=47=b2
/a21
=l=2
Генеральный элемент: alk
=а21
=10
Переход к новой симплексной таблице:
B2
= b1
/ а21
=472/10=47
c=C-ck
bс
=c-c2
b1
=0-(-3)*47=148
alj
=alj
/alk
 10/10=1 10/10=1
 0/10=0 0/10=0
 =0/10=0 =0/10=0
 =1/10 =1/10
 0/10=0 0/10=0
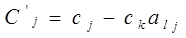
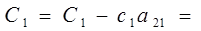 -3-(-3)*1=0 -3-(-3)*1=0
 0-(-3)*0=0 0-(-3)*0=0
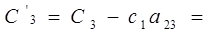 2/9-(-3)*0=2/9 2/9-(-3)*0=2/9
 0-(-3)*1/10=0+3/10=3/10 0-(-3)*1/10=0+3/10=3/10
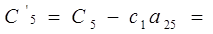 0-(-3)*0=0 0-(-3)*0=0

 =6 =6
 =774-10*47=304 =774-10*47=304

 1/3-1/3=0 1/3-1/3=0
 1-1*0=1 1-1*0=1
 1/27-1/27*0=1/27 1/27-1/27*0=1/27
 0-0*1/10=0 0-0*1/10=0
 0-0*0=0 0-0*0=0
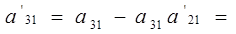 10-10*1=0 10-10*1=0
 0-0*0=0 0-0*0=0
 0-0*0=0 0-0*0=0
 0-0*1/10=0 0-0*1/10=0
 1-1*0=1 1-1*0=1
Третья симплексная таблица
| Оценка базисных переменных |
Базисные переменные |
Свободные члены |
5 |
6 |
0 |
0 |
0 |
| С
|
Х |
Р0
|
Р1
|
Р2
|
Р3
|
Р4
|
Р5
|
| 6 |
Х2
|
6 |
0 |
1 |
1/27 |
0 |
0 |
| 5 |
Х1
|
47 |
1 |
0 |
0 |
1/10 |
0 |
| 0 |
Х5
|
304 |
0 |
0 |
0 |
0 |
1 |
| С |
148 |
0 |
0 |
2/9 |
3/10 |
0 |
Проверка опорного плана на оптимальность:
СК
=min{Сj
(cj
|
<0)}=min (0;0;2/9;3/10;0)=0
Полученный план оптимален.
В векторном виде опорный план выглядит:
 =(47;6;0;0;304) =(47;6;0;0;304)
С( )=148 )=148
Экономическая интерпретация задачи:
Объём производства будет оптимальным при достижении максимальной прибыли-148 д.ед., и при объёме производства товара-6 шт. и 47 шт.
|