Световод: уравнение, типы волн в световодах. Критические длины и частоты
1. Уравнение передачи по световоду
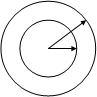
Рассмотрим волоконный световод без потерь двухслойной конструкции, приведенный на рис. 1
b
n2
n1
a
Рис. 1
|
Для описания поведения электромагнитного поля в сердечнике (0<r<a) и в оболочке (a<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции внутри сердечника при r=0 должны быть конечными, а в оболочке описывать спадающее поле.
Для определения основных параметров световодов (критической частоты, волнового числа, скорости передачи и др.) воспользуемся основными уравнениями электродинамики – уравнениями Максвелла, которые для диэлектрических волноводов имеют вид:
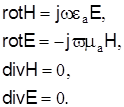 (1) (1)
Уравнения Максвелла справедливы для любой системы координат. Для направляющих систем эти уравнения наиболее часто применяются в цилиндрической системе координат, ось Z которой совместим с оптической осью световода:
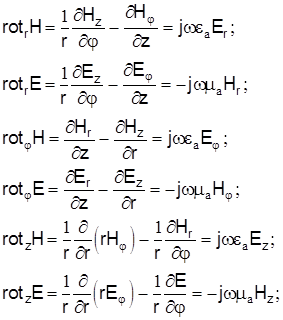 (2) (2)
Для решения инженерных задач электродинамики необходимо знать продольные составляющие полей Еz
и Hz
. Их можно получить следующим образом. Преобразуем первое из уравнений Максвелла (1) к виду
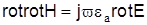 . .
Тогда, используя соотношение 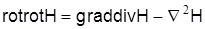 , а также учитывая, что divH=0, получим , а также учитывая, что divH=0, получим
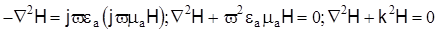 , ,
где 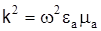 - волновое число световода. - волновое число световода.
Поступая аналогично со вторым уравнением Максвелла (2), получим 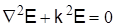 . .
Отсюда следует, что продольные электромагнитные составляющие векторов Ez
и Hz
удовлетворяют уравнениям
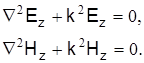
Где 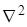 – оператор Лапласа. – оператор Лапласа.
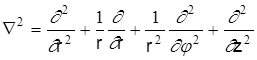 , ,
Тогда для продольных составляющих Ez
и Hz
в цилиндричееской системе координат получим дифференциальные уравнения второго порядка:
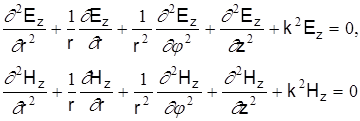 (3) (3)
Допустим, что напряженность электромагнитного поля в направлении оси Z меняется по экспоненциальному закону, т.е.  , где А – любая составляющая векторов Е или Н; , где А – любая составляющая векторов Е или Н; 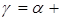 j j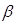 - коэффициент распространения. Тогда первая и вторая производные определятся - коэффициент распространения. Тогда первая и вторая производные определятся
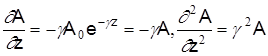 . .
Для составляющей Еz
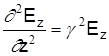 . .
Подставляя полученное значениe в уравнения (3), получим
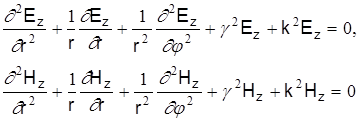
Введем обозначение 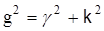 – поперечное волновое число световода. Тогда для сердечника световода имеем – поперечное волновое число световода. Тогда для сердечника световода имеем
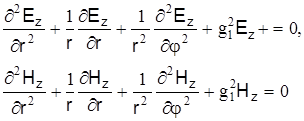 (4) (4)
где 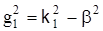 (без учета затухания) – поперечное волновое число сердечника; k1
– волновое число сердечника с коэффициентом преломления n1
, (без учета затухания) – поперечное волновое число сердечника; k1
– волновое число сердечника с коэффициентом преломления n1
, 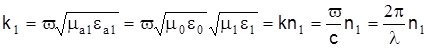 . .
Решение уравнений (4) для сердечника следует выразить через цилиндрические функции первого рода – функции Бесселя, имеющие конечные значения при r=0. Поэтому можно написать
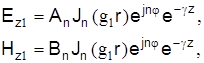 (5) (5)
где Аn
и Вn
– постоянные интегрирования.
Воспользовавшись уравнениями (2), рассмотрим связь между поперечными и продольными компонентами поля. В частности, для составляющей Еr
имеем
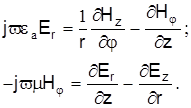
Возьмем производную от второго выражения по 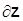
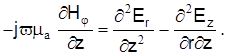
Учитывая, что 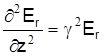 , а , а 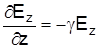 , то , то 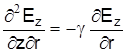
Тогда
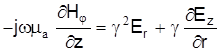 или или 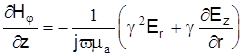
Подставим данное выражение в уравнение для Еr
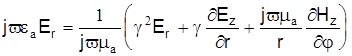 или или
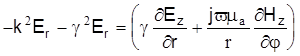 . .
Окончательно получим 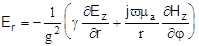 . .
Аналогично можно установить связь между продольными и другими поперечными компонентами поля
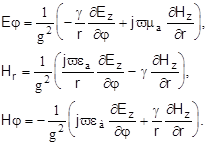
Воспользовавшись уравнениями (5) возьмем соответствующие производные
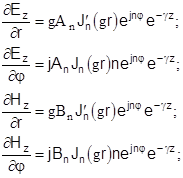
Тогда выражения для поперечных составляющих электрического и магнитного полей в сердечнике световода, полагая, что 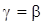 , имеют вид (множитель , имеют вид (множитель 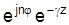 не пишем): не пишем):
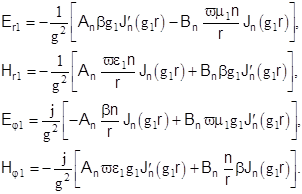 (6) (6)
Для оболочки имеем аналогичную систему уравнений:
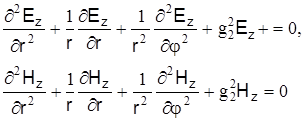
где 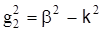 (без учета затухания) – поперечное волновое число оболочки световода; k2
– волновое число оболочки с коэффициентом преломления n2
, (без учета затухания) – поперечное волновое число оболочки световода; k2
– волновое число оболочки с коэффициентом преломления n2
, 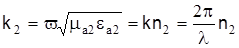 . .
Для решения данных уравнений, исходя из условия, что при 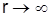 поле должно стремиться к нулю, следует использовать цилиндрические функции третьего рода – функции Ганкеля: поле должно стремиться к нулю, следует использовать цилиндрические функции третьего рода – функции Ганкеля:
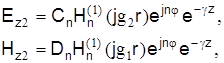
где Сn
, Dn
– постоянные интегрирования.
Тогда для поперечных составляющих поля в оболочке можно написать следующие выражения:
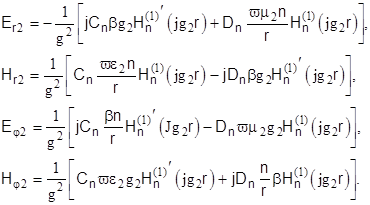 (7) (7)
Постоянные интегрирования Аn
, Вn
, Сn
, Dn
могут быть определены на основании граничных условий. Используем условия равенства тангенциальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердечник-оболочка (при r=а):
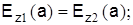 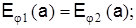
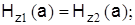 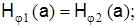
Найдя постоянные интегрирования и подставив их в уравнения, после соответствующих преобразований получим следующее трансцендентное уравнение:
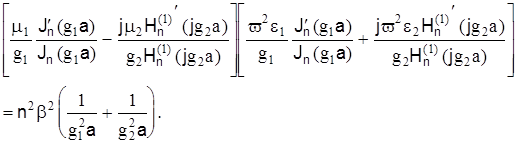 (8) (8)
Полученные уравнения дают возможность определить неизвестные постоянные и найти структуру поля в сердечнике и оболочке волоконного световода. В общем случае уравнения имеют ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны или модой.
световод уравнение интегрирование волна
2. Типы волн в световодах
В сетоводах могут существовать два типа волн: симметричные E0m
, H0m
несимметричные дипольные EHnm
, HEnm
. В индексе n – число изменений поля по диаметру; m – число изменений поля по периметру. Симметричные волны электрические Е0m
и магнитные H0m
имеют круговую симметрию (n=0).
Раздельное распространение по световоду несимметричных волн типа невозможно. В световоде они существуют только совместно, т.е. имеются продольные составляющие Е и Н. Эти волны называются смешанными, дипольными и обозначаются через HЕnm
, если поле в поперечном сечении напоминает поле Н, или EНnm
, если поле в поперечном сечении ближе к волнам Е.
Из всей номенклатуры смешанных волн в оптических кабелях наибольшее применение получила волна типа НЕ11
(или ЕН10
). На этой волне работают одномодовые световоды, имеющие наибольшую пропускную способность
Представляет интерес сопоставить указанную классификацию электромагнитных волн с лучевой классификацией.
Как уже отмечалось, по волоконным световодам возможна передача двух видов лучей: меридиональных и косых. Меридиональные лучи расположены в плоскости, проходящей через ось волоконного световода. Косые лучи не пересекают ось световода.
Меридиональным лучам соответствуют симметричные электрические Е0m
и магнитныеH0m
волны, косым лучам – несимметричные гибридные EНnm
и HЕnm
волны.
Если точеченый источник излучения расположен по оси световода, то имеются только меридиональные лучи и соответственно симметричные волны Е0m
, H0m
. Если же точечный источник расположен вне оси световода или имеется сложный источник, то появляются одновременно как меридиональные, так и косые лучи и свойственные им симметричные Е0m
, H0m
и несимметричные гибридные (EНnm
и HЕnm
) волны.
Несимметричные волны типа Enm
и Hnm
в волоконных световодах существовать не могут. Эти волны возбуждаются только в металлических волноводах.
Основное уравнение передачи по волоконному световоду для случая 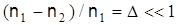 может быть значительно упрощено применительно к различным типам волн. может быть значительно упрощено применительно к различным типам волн.
Для симметричных волн правая часть уравнения (8) равна нулю, тогда имеем два различных уравнения для электрической Е0m
и магнитной Н0m
волн:
для Е0m
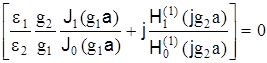 (9) (9)
для Н0m
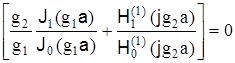
Для смешанных дипольных волн можно получить следующие приближенные уравнения:
для НЕnm
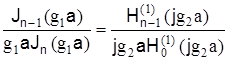 (10) (10)
для ЕНnm
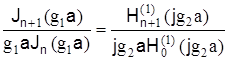
Для области часто, далеко отстоящих от критической частоты, можно воспользоваться более простыми выражениями:
для НEnm
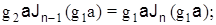
для ЕHnm
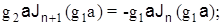
Данные выражения позволяют определять структуру поля, параметры волн и характеристики волоконного световода при различных типах волн и частотах.
Каждый тип волны (мода) имеют свою критическую частоту и длину волны. Наличие критической частоты в волоконных световодах объясняется тем, что при очень высоких частотах почти вся энергия концентрируется внутри сердечника световода, а с уменьшением частоты происходит перераспределение поля и энергия переходит в окружающее пространство. При определенной частоте fo
– критической, или частоте отсечки, поле больше не распространяется вдоль световода и вся энергия рассиевается в окружающим пространстве.
Ранее были приведены следующие соотношения:
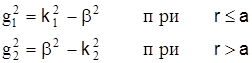
где 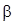 - коэффициент фазы в световоде; - коэффициент фазы в световоде;
k1
и k2
– волновое число соответственно сердечника
и оболочки световода:
g1
и g2
– поперечное волновое число соответственно
для сердечника и оболочки.
а – радиус сердечника волокна.
Учитывая, что

получим  . .
Полагая, что r=a, произведем сложение левых и правых частей приведенных выражений
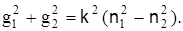
Для определения критической частоты fo
надо принять g2
=0. При всех значениях g2
>0 поле концентрируется в сердечнике световода, а при g2
=0 оно выходит из сердечника и процесс распространения по световоду прекращается. По закону геометрической оптики условие g2
=0 соответствует углу полного внутреннего отражения, при котором отсутствует преломленная волна, а есть толь падающая и отраженная волны. Тогда при g2
=0 имеем 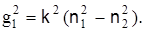
Подставив в эту формулу значение 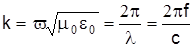 , получим , получим 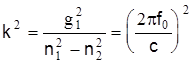 , откуда критическая частота световода , откуда критическая частота световода 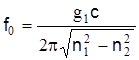 . (11) . (11)
Умножив числитель и знаменатель на параметр а (радиус сердечника), получим значение критической частоты
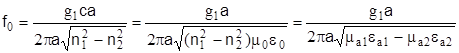 (12) (12)
и критической длины волны
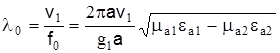 , (13) , (13)
где g1
a – корни бесселевых функций.
Так как световоды изготавливаются из немагнитных материалов (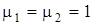 ), то ), то
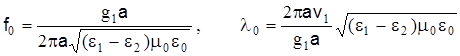 . .
Принципиально аналогичный результат можно получить лучевым методом непосредственно из законов геометрической оптики путем сопоставления падающей, отраженной и преломленной волн на границе сердечник-оболочка световода.
Анализируя полученные соотношения, можно сказать, что чем толще сердечник световода и чем больше отличаются 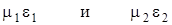 , тем больше критическая длина волны и соответственно ниже критическая частота волоконного световода. Из формул видно также, что при равенстве оптических характеристик, в первую очередь диэлектрической проницаемости сердечника и оболочки, т.е. при , тем больше критическая длина волны и соответственно ниже критическая частота волоконного световода. Из формул видно также, что при равенстве оптических характеристик, в первую очередь диэлектрической проницаемости сердечника и оболочки, т.е. при 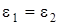 , критическая длина волны , критическая длина волны 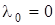 , а критическая частота , а критическая частота 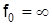 и передача по такому световоду невозможна. Это имеет свое логическое обоснование: как уже сказано, волоконный световод работает на принципе многократного отражения от границы оптических несоответствий сердечника и оболочки, и эта граница является направляющей средой распространения электромагнитной энергии. При и передача по такому световоду невозможна. Это имеет свое логическое обоснование: как уже сказано, волоконный световод работает на принципе многократного отражения от границы оптических несоответствий сердечника и оболочки, и эта граница является направляющей средой распространения электромагнитной энергии. При 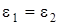 световод перестает действовать как направляющая система передачи. световод перестает действовать как направляющая система передачи.
Для определения критических частот различных типов волн рассмотрим корни ранее полученного выражения бесселевых функций J0m
(g1
a) для симметричных и Jnm
(g1
a) для несимметричных волн. Эти равенства дают бесконечное число корней, значения которых приведены в табл. 1.
Таблица 1
| n |
Значение корня (g1
a) при m, равном |
Тип волны |
0
1
1
2
2
|
2,405
0,000
3,832
2,445
5,136
|
5,520
3,832
7,016
5,538
8,417
|
8,654
7,016
10,173
8,665
11,620
|
Е, Н
НЕ
ЕН
НЕ
ЕН
|
Рассмотрим физический смысл приведенных в табл. 1 корней бесселевых функций g1
a. Поскольку при отсечке g2
=0, т.е. 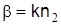 , то из выражения , то из выражения 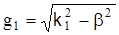 имеем имеем
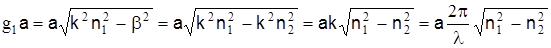
Последнее выражение обратно пропорционально 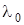 , т.е. прямо пропорционально критической частоте f0
. Кроме того, оно включает в себя исходные параметры волокна: а, n1
, n2
. Данное выражение носит название нормированной частоты
и в этом виде часто используется в световодной технике. Таким образом, нормированная частота , т.е. прямо пропорционально критической частоте f0
. Кроме того, оно включает в себя исходные параметры волокна: а, n1
, n2
. Данное выражение носит название нормированной частоты
и в этом виде часто используется в световодной технике. Таким образом, нормированная частота
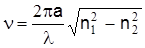 , ,
где 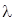 - длина волны в вакууме. - длина волны в вакууме.
При такой трактовке табл. 1 содержит нормированные частоты 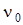 для волн, тип которых указан в правой колонке таблицы, а индекс nm составлен из чисел левого столбца и верхней строки соответствующей клетке, в которой находится данная величина для волн, тип которых указан в правой колонке таблицы, а индекс nm составлен из чисел левого столбца и верхней строки соответствующей клетке, в которой находится данная величина 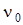 . Каждой . Каждой 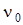 соответствует критическая частота f0
. соответствует критическая частота f0
.
При 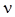 < <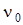 имеем f<f0
, т.е. частота меньше критической и волна по сердечнику волокна не распространяется, другими словами не существует. Область существования волны, имеющей нормированную частоту отсечки имеем f<f0
, т.е. частота меньше критической и волна по сердечнику волокна не распространяется, другими словами не существует. Область существования волны, имеющей нормированную частоту отсечки 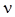 > >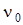 составляет f>f0
. составляет f>f0
.
Из табл. 1 видно, что для несимметричной волны НЕ11
значение 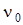 =0; следовательно, эта волна не имеет критической частоты и может распространяться при любой частоте и диаметре сердечника. Все другие волны не распространяются на частотах ниже критической. Табл.1 можно преобразовать и привести к следующему виду (табл. 2) =0; следовательно, эта волна не имеет критической частоты и может распространяться при любой частоте и диаметре сердечника. Все другие волны не распространяются на частотах ниже критической. Табл.1 можно преобразовать и привести к следующему виду (табл. 2)
Таблица 2
| Диапазон частот |
Дополнительные моды |
Число мод |
0,000–2,405
2,405–3,832
3,832–5,316
5,316–5,520
5,520–6,380
6,380–7,016
7,016–7,588
7,588–8,417
8,417–11,620
|
HE11
H01
, E01
, HE21
HE12
, EH11
, HE31
EH21
, HE41
H02
, E02
, HE22
EH31
, HE51
HE13
, EH12
, HE32
EH41
, HE61
EH22
, E03
, H03
, EH13
, HE23
, EH23
|
2
6
12
16
20
24
30
34
40
|
Из табл. 2 следует, что с увеличением частоты появляются новые типы волн. Так, начиная с 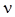 =2,405 появляются волны H01
, E01
, HE21
, при =2,405 появляются волны H01
, E01
, HE21
, при 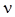 =3,832 возникают дополнительные волны HE12
, EH11
, HE31
и т.д. =3,832 возникают дополнительные волны HE12
, EH11
, HE31
и т.д.
Итак, интервал значений 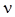 =g1
a, при которых в световоде распространяется лишь один тип волн НЕ11
, находится в пределах 0< =g1
a, при которых в световоде распространяется лишь один тип волн НЕ11
, находится в пределах 0<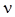 <2,405, поэтому при выборе частоты передачи или толщины сердечника одномодового световода исходят из этого условия: <2,405, поэтому при выборе частоты передачи или толщины сердечника одномодового световода исходят из этого условия:
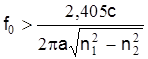 . (14) . (14)
Одномодовый режим практически достигается при применении очень тонких волокон, равных по диаметру длине волны 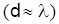 . Кроме того, надо стремиться к уменьшению разницы между показателями преломления сердечника и оболочки . Кроме того, надо стремиться к уменьшению разницы между показателями преломления сердечника и оболочки 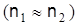 . .
Диаметр сердечника волоконного световода для одномодовой передачи может быть определен из следующей формулы:
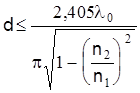 . (15) . (15)
Пример: для световода из стекловолокна с показателем преломления сердечника 1,48 и показателем преломления оболочки 1,447 при волне Е01
длиной 1,55 мкм для одноволновой передачи получим
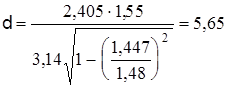 мкм мкм
|