| Московский государственный университет им. М. В. Ломоносова
Физический факультет
Движение тела переменной
массы
Курсовая работа
по курсу «компьютерные методы в физике»
студента 214 группы
Юшкова Константина
Преподаватель
доцент С. А. Шлёнов
Москва - 2003
Аннотация
В задаче рассматривается пример старта ракеты с поверхности различных планет солнечной системы и их спутников; сравниваются характеристики ракет с различным числом ступеней и их пригодность для выполнения различных задач; исследуется влияние сил инерции на движение ракеты в процессе полёта; находится необходимая масса топлива для полёта с некоторых планет солнечной системы.
Выполнить компьютерное моделирование движения тела переменной массы на примере старта ракеты с поверхности планеты.
Рассмотрим движение тела переменной массой во внешнем силовом поле. Уравнение Ньютона в общем виде
 , (1) , (1)
переписанное в системе центра масс, примет вид:
 , (2) , (2)
где 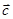 - скорость истечения газа. Вводя обозначение - скорость истечения газа. Вводя обозначение 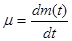 и учитывая характер внешнего силового поля и учитывая характер внешнего силового поля 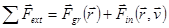 , образованного силами притяжения и инерции, перепишем уравнение (2) как , образованного силами притяжения и инерции, перепишем уравнение (2) как
 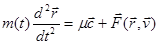 (3) (3)
где 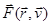 - сумма внешних сил, действующих на тело; - сумма внешних сил, действующих на тело;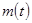 - масса ракеты. Уравнение (3) называется уравнением Мещерского [1, 2]. Величина - масса ракеты. Уравнение (3) называется уравнением Мещерского [1, 2]. Величина  представляет собой реактивную силу тяги. представляет собой реактивную силу тяги.
Рассмотрим движение ракеты в отсутствие внешних сил. Уравнение движения в скалярном виде (с учётом того, что векторы 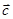 и и  противоположно направлены) будет иметь вид: противоположно направлены) будет иметь вид:
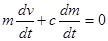 . (4) . (4)
Это уравнение с разделяющимися переменными; проинтегрировав его в конечных пределах
 , (5) , (5)
получим:
 ; (6) ; (6)
эта формула называется формулой Циолковского [3]. Из неё следует, что для сообщения телу массой 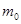 конечной скорости v
требуется, без учёта затрат на преодоление сил тяжести, масса топлива, равная конечной скорости v
требуется, без учёта затрат на преодоление сил тяжести, масса топлива, равная
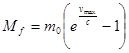 . (7) . (7)
Рассмотрим теперь модель, в которой учитывается однородное поле тяжести  (знак минус означает, что поле направленно против движения ракеты), можно получить (знак минус означает, что поле направленно против движения ракеты), можно получить
 , (8) , (8)
где  - полное время работы двигателей. При постоянном расходе топлива - полное время работы двигателей. При постоянном расходе топлива
 (9); (9);
так как  , то уравнение (8) - трансцендентное уравнение относительно , то уравнение (8) - трансцендентное уравнение относительно 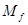 . Максимальное ускорение одноступенчатой ракеты в такой модели определяется соотношением . Максимальное ускорение одноступенчатой ракеты в такой модели определяется соотношением  , то есть , то есть
 , (10) , (10)
так как в широком диапазоне реализуемых начальных условий  . .
| 
Рис. 1. Выбор локальной системы координат
|
В данной задаче производится численное интегрирование уравнения Мещерского для движения ракеты во внешнем силовом поле. Рассматривается двумерная задача движения ракеты, стартующей с экватора планеты в её экваториальной плоскости. Задача рассматривается в декартовой системе координат с началом отсчёта в точке старта ракеты (см. рис. 1
). Начальный угол старта ракеты может изменяться в направлении вращения планеты. При движении тела учитывается изменение силы тяжести с высотой[1]
и центробежная сила инерции, а также имеется возможность учитывать или не учитывать силу Кориолиса  ( ( – угловая скорость вращения планеты; для некоторых рассматриваемых планет величина ω не определена). Ракета считается материальной точкой. Таким образом, в выбранной системе отсчета (
x
,
y
)
уравнения движения (2) принимают вид: – угловая скорость вращения планеты; для некоторых рассматриваемых планет величина ω не определена). Ракета считается материальной точкой. Таким образом, в выбранной системе отсчета (
x
,
y
)
уравнения движения (2) принимают вид:
 , (11) , (11)
где 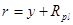 - расстояние от центра планеты до точки нахождения ракеты, - расстояние от центра планеты до точки нахождения ракеты,  - угол между направлением движения ракеты и вертикалью; сила тяги - угол между направлением движения ракеты и вертикалью; сила тяги  определяется скоростью истечения газа, которая постоянна по величине ( определяется скоростью истечения газа, которая постоянна по величине (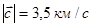 ) и направлена противоположно ) и направлена противоположно  . .
В программе реализована возможность выбирать режим работы двигателя:
1.
Неограниченное ускорение (одноступенчатый режим).
Расход топлива и сила тяги двигателя постоянны на протяжении всего процесса ускорения и определяются при запуске.
2.
Двухступенчатый режим.
Два фиксированных режима. Начальный расход топлива определяется при запуске; при израсходовании 0.5 начальной массы топлива расход уменьшается в 2 раза, а масса ракеты единоразово уменьшается на 10 т. В дальнейшем режим работы двигателей не меняется. Максимальное ускорение a
max
=½ a
1
[2]
.
3.
Трёхступенчатый режим.
После отработки половины топлива расход уменьшается в 2 раза, а масса на 15 т. После отработки 90% начальной массы топлива расход уменьшается ещё в 2 раза, а масса на 5 т. Максимальное ускорение a
max
=¼ a
1
4.
Режим с ограниченным ускорением.
Авторегулируемый режим. Ускорение ракеты ограничено величиной 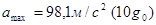 . Если ускорение превышает величину . Если ускорение превышает величину  , то расход топлива уменьшается до такой величины, чтобы ускорение стало равно , то расход топлива уменьшается до такой величины, чтобы ускорение стало равно  . Таким образом, ускорение системы поддерживается в диапазоне . Таким образом, ускорение системы поддерживается в диапазоне 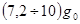 ; за счёт этого расход топлива и сила тяги постепенно уменьшаются с высотой. ; за счёт этого расход топлива и сила тяги постепенно уменьшаются с высотой.
Интегрирование уравнений движения (11) производится по схеме Эйлера с фиксированным шагом интегрирования 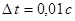
 (12)
(12)
Выбор шага интегрирования производился с учётом анализа работы программы. Увеличение шага интегрирования приводит к потере устойчивости решения. Например, при  нарушается устойчивость решения. Выбранное значение нарушается устойчивость решения. Выбранное значение  обеспечивает в исследуемом диапазоне начальных условий, приближённых к реальным параметрам ракет, непрерывность и гладкость (в пределах погрешностей округления) решений по параметрам M
f
, m
0
, μ
, требуемые соответствующими теоремами (см. [4], гл.VII, §3). При таком выборе обеспечивает в исследуемом диапазоне начальных условий, приближённых к реальным параметрам ракет, непрерывность и гладкость (в пределах погрешностей округления) решений по параметрам M
f
, m
0
, μ
, требуемые соответствующими теоремами (см. [4], гл.VII, §3). При таком выборе  решение задачи (12) с соответствующими граничными условиями решение задачи (12) с соответствующими граничными условиями
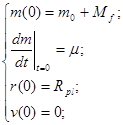 (13)
(13)
является устойчивым (см. [4], гл.VII, §6).
Дальнейшее уменьшение шага интегрирование до величин, меньших 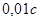 замедляет работу программы, но практически не влияет на решение задачи. замедляет работу программы, но практически не влияет на решение задачи.
Программа реализована с помощью двух потоков. Основной поток обрабатывается оконной функцией WindowFunc и отвечает за обработку системных команд и команд меню. Дополнительный поток, описываемый функцией ThreadProc, производит необходимые вычисления и выводит на экран траекторию движения ракеты в реальном времени, а также графики, описывающие движение, после выполнения вычислений. В процессе вычисления на каждом шаге все основные параметры выводятся в файл, имя которого может быть указано в пункте меню Параметры->Файл Вывода (по умолчанию ballista.dat). Перед началом вычисления определяются параметры запуска: планета, с которой производится запуск, полезная масса 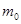 , масса топлива , масса топлива 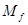 , начальный расход топлива μ, угол запуска , начальный расход топлива μ, угол запуска 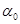 . Также выбирается масштаб изображения (измеряется в пикселях/км); для корректировки скорости работы программы можно ввести задержку (измеряется в . Также выбирается масштаб изображения (измеряется в пикселях/км); для корректировки скорости работы программы можно ввести задержку (измеряется в 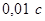 на каждом шаге). По ходу моделирования полёта траектория движения ракеты выводится на экран красным цветом, если двигатели работают, и жёлтым, если топливо кончилось, и продолжается движение ракеты в поле тяжести. Выводится также текущая продолжительность полёта, скорость ракеты, 2-я космическая скорость в текущей точке и процентное количество оставшегося топлива. По завершении вычисления, на экран выводятся графики зависимости от времени высоты, скорости и ускорения ракеты (ускорение нормируется в единицах на каждом шаге). По ходу моделирования полёта траектория движения ракеты выводится на экран красным цветом, если двигатели работают, и жёлтым, если топливо кончилось, и продолжается движение ракеты в поле тяжести. Выводится также текущая продолжительность полёта, скорость ракеты, 2-я космическая скорость в текущей точке и процентное количество оставшегося топлива. По завершении вычисления, на экран выводятся графики зависимости от времени высоты, скорости и ускорения ракеты (ускорение нормируется в единицах  ). Программа переходит в режим ожидания. ). Программа переходит в режим ожидания.
В пункте меню Параметры->дополнительно выбираются варианты применяемых моделей ускорения и учёта сил инерции (силы Кориолиса).
Определим максимальные достигнутые в различных режимах скорости при одинаковых параметрах запуска.
Запуск ракеты производится с поверхности Земли при начальных условиях  , ,  , , 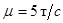 , ,  . Варьируется режим ускорения. Находятся максимальные достигнутые скорости и ускорения ракет, представленные в таблице 1
. Видно, что на начальной стадии полёта все режимы работают одинаково, однако на завершающих стадиях, когда полная масса ракеты значительно уменьшается, существенно сказываются особенности режимов. В режиме с ограниченным ускорением расход топлива уменьшается постепенно, а скорость увеличивается по закону, близкому к линейному, со средним ускорением . Варьируется режим ускорения. Находятся максимальные достигнутые скорости и ускорения ракет, представленные в таблице 1
. Видно, что на начальной стадии полёта все режимы работают одинаково, однако на завершающих стадиях, когда полная масса ракеты значительно уменьшается, существенно сказываются особенности режимов. В режиме с ограниченным ускорением расход топлива уменьшается постепенно, а скорость увеличивается по закону, близкому к линейному, со средним ускорением  . В других режимах ускорения возрастают до величин, значительно превышающих физиологический порог переносимости длиннодействующего ускорения . В других режимах ускорения возрастают до величин, значительно превышающих физиологический порог переносимости длиннодействующего ускорения  (см. [3], стр. 417). (см. [3], стр. 417).
| Кол-во ступеней
|
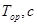
|
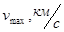
|
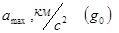
|
| 1 ступень
|
70,0
|
11,88
|
1,75 (178,5)
|
| 2 ступени
|
101,0
|
11,39
|
0,87 (88,6)
|
| 3 ступени
|
109,0
|
10,81
|
0,43 (43,8)
|
| ограниченный
|
145,8
|
11,22
|
0,09 (10,0)
|
| Таблица 1. Сравнение режимов с разным числом ступеней (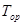 ‑ полное врема работы двигателей). ‑ полное врема работы двигателей).
|
| 
Рис. 2. Зависимость массы ракеты от времени при различных режимах ускорения
|
Из рис. 3
видно, что в режиме 4
скорость набирается существенно медленнее, чем в режимах с несколькими ступенями. Так, например, скорость 10 км/с
достигается в одноступенчатом режиме за 69 с
, в двухступенчатом за 100 с
, а в режиме с ограничением ускорения за 130 с
.
| 
Рис. 3. Зависимость скорости ракеты от времени в различных режимах ускорения
|
| 
Рис. 4. Зависимость от времени ускорения ракеты в режиме с ограниченным ускорением.
|
Также видно, сравнивая режимы с фиксированными ступенями, что эффективность разгона падает с ростом числа ступеней, зато уменьшаются перегрузки ракеты. Так как расчётные ускорения слишком велики, введён режим с ограниченным ускорением, позволяющий более эффективно моделировать реальные полёты.
Сравним основные параметры полёта с учётом и без учета действия силы Кориолиса.
Запуск производится с поверхности Земли с начальными условиями  , , 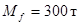 , , 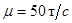 , ,  . в режиме ограниченного ускорения. . в режиме ограниченного ускорения.
По результатам моделирования определено отклонение ракеты от начальной траектории (т.е. траектории без учёта силы Кориолиса). На рис.
6
представлены зависимости отклонений по координатам в зависимости от высоты.
 
Рис.5. Зависимость отклонения ракеты по осям X
(a
) и Y
(b
), вызванного силой Кориолиса, от высоты.
Таким образом, анализируя графики рис. 6
, можно сказать, что сила Кориолиса слабо влияет на зависимости высоты и скорости от времени (при 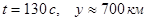 отличие по y
составляет всего 100 м
, а по x
- 10,4 км
; разность скоростей составляет менее 1 м/с
и не превосходит погрешности округления), но существенно влияет на наведение ракеты, и, соответственно, должна учитываться при расчёте алгоритмов навигации и ориентации ракеты. Например, если ставится задача вывода ракеты в данную точку орбиты, то отклонение ракеты от первоначальной траектории в горизонтальном направлении есть величина порядка 10 км, что недопустимо при решении данной задачи. Для расчёта необходимой начальной массы топлива влиянием кориолисова ускорения можно пренебречь для упрощения модели, так как вертикальные отклонения составляют величины порядка 100 м
. отличие по y
составляет всего 100 м
, а по x
- 10,4 км
; разность скоростей составляет менее 1 м/с
и не превосходит погрешности округления), но существенно влияет на наведение ракеты, и, соответственно, должна учитываться при расчёте алгоритмов навигации и ориентации ракеты. Например, если ставится задача вывода ракеты в данную точку орбиты, то отклонение ракеты от первоначальной траектории в горизонтальном направлении есть величина порядка 10 км, что недопустимо при решении данной задачи. Для расчёта необходимой начальной массы топлива влиянием кориолисова ускорения можно пренебречь для упрощения модели, так как вертикальные отклонения составляют величины порядка 100 м
.
Проверяется соответствие результатов моделирования полёта формуле Циолковского (6).
Зафиксируем полезную массу груза 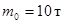 и стартовую массу топлива и стартовую массу топлива  и исследуем зависимость максимальной достигнутой скорости ракеты от расхода топлива. Согласно (8) и (9) должно наблюдаться асимптотическое стремление по гиперболическому закону и исследуем зависимость максимальной достигнутой скорости ракеты от расхода топлива. Согласно (8) и (9) должно наблюдаться асимптотическое стремление по гиперболическому закону 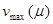 к величине к величине 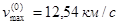 , определяемой формулой (6). Результаты этого исследования представлены на рис.
6
. Теоретическая кривая построена по формуле (8); для сравнения представлена соответствующая зависимость , определяемой формулой (6). Результаты этого исследования представлены на рис.
6
. Теоретическая кривая построена по формуле (8); для сравнения представлена соответствующая зависимость  для режима с ограниченным ускорением. для режима с ограниченным ускорением.
| 
Рис. 6. Зависимость максимальной скорости от расхода топлива
|
Как видно из рис. 6
, применяемая модель одноступенчатой ракеты достаточно хорошо соответствует теоретической модели, описываемой формулой Циолковского (8),однако, так как данная модель не учитывает уменьшения силы тяжести с выотой, то имеется систематическая погрешность: на рис. 6
видно, что развиваемые скорости превышают теоретический предел на величины порядка 0,05 км/с
. В модели с ограниченным ускорением максимальная скорость выходит на константу (при данных начальных условиях ≈11,31 км/с), меньшую, чем  . .
Также исследуем зависимость развиваемой скорости от стартовой массы топлива. На Рис 7
изображены две кривые v
max
(M
f
) для одноступенчатого режима со значениями μ
=3 т/c (a
max
≈107g0
) и μ
=6 т/c (a
max
≈217g0
), а также для ограниченного режима (μ
=6 т/c). При μ
≤3, т/c ограниченный режим эффективнее, чем одноступенчатый; при μ
≥3,4 т/c в одноступенчатом режиме требуется меньше топлива, однако при этом развивается ускорение a
max
≈120g0
, что значительно больше, чем в ограниченном режиме. Для двухступенчатого режима эффективность большая, чем для ограниченного, достигается при μ
≥6,8 т/c (a
max
≈120g0
); для трёхступенчатого наибольшая эффективность достигается при M
f
=312 т, μ=15,4 т/c (a
max
≈137g0
).
| 
Рис. 7. Зависимость максимальной скорости от стартовой массы топлива
|
Заштрихованными значками на рис 7
нанесены точки, в которых максимальная достигнутая скорость равна второй космической в момент прекращения работы двигателей. Так как с высотой величина второй космической скорости монотонно уменьшается, а при увеличении стартовой массы топлива увеличиваются как максимальная скорость ракеты, так и высота, на которой она достигается, то при заданном расходе топлива можно однозначно определить стартовую массу топлива, необходимую для достижения второй космической скорости.
Найдем минимальную массу топлива, необходимую для вертикального старта модуля с полезной массой  с поверхности некоторых планет солнечной системы и достижения второй космической скорости.
с поверхности некоторых планет солнечной системы и достижения второй космической скорости.
С учётом исследования, проведённого в пунктах 2
и 3
, а также формулы Циолковкого (8), можно сказать, что с увеличением времени работы двигателей стартовая масса также должна увеличиваться для достижения той же конечной скорости, и основным критерием выбора режима полёта можно считать максимальное допустимое ускорение. В одноступенчатом режиме для минимизации стартовой массы необходимо увеличивать расход топлива, что, в конечном счете, приводит к увеличению ускорения. В связи с этим для исследования выбирается ограниченный режим ускорения, сила Кориолиса не учитывается.
| 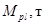
|

|
| Луна
|
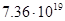
|
10
|
| Марс
|

|
34
|
| Земля
|
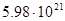
|
282
|
| Уран
|
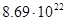
|
6450
|
| Таблица 2. Необходимая масса топлива 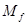 при старте ракеты с различных планет с массой при старте ракеты с различных планет с массой
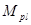
|
Результаты моделирования, приведённые в таблице 2
, показывают, что для возврата посадочного модуля с небесных тел тяжелее Земли требуется снабжение их соответствующим количеством топлива, что делает подобные проекты практически неосуществимыми при существующей технике ракетных полётов.
|
|

|

|
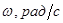
|
| Меркурий
|
0.054
|
2500
|

|
| Венера
|
0.815
|
6052
|

|
| Земля
|
1.0
|
6378
|
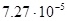
|
| Луна
|
0.0123
|
1738
|
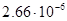
|
| Марс
|
0.108
|
3394
|
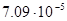
|
| Юпитер
|
317.8
|
69780
|

|
| Ио
|
0.015
|
1820
|
-
|
| Европа
|
0.0079
|
1565
|
-
|
| Ганимед
|
0.0248
|
2640
|
-
|
| Каллисто
|
0.018
|
2420
|
-
|
| Сатурн
|
95,1
|
2425
|
-
|
| Титан
|
0.023
|
2425
|
-
|
| Уран
|
14.54
|
25400
|
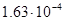
|
| Нептун
|
17.22
|
22300
|

|
| Таблица 3. Характеристики планет солнечной системы и их спутников: отношение массы к массе Земли, экваториальный радиус, угловая скорость суточного вращения.
|
Литература
- С.Э.Хайкин, Физические основы механики,М., «Наука», 1971.
- С.П.Стрелков, Механика, М., «Наука», 1965.
3. Космонавтика: энциклопедия, под ред. Г.П.Глушко,
М., «Советская Энциклопедия», 1985.
4. В.В.Степанов, Курс дифференциальных уравнений, М., Гостехиздат, 1953.
[1]
применяется модель поля тяжести равномерной сферы с потенциалом  . .
[2]
Под a
1
подразумевается максимальное ускорение в одноступенчатом режиме.
|