Высшая математика

Страница 3

Решение:

Ответ:

Задание №14. Вопрос №2.

Вычислить несобственный интеграл (или установить его расходимость) .

Решение:

Ответ:

Данный несобственный интеграл – расходящийся.

Задание №15. Вопрос №6.

Решить уравнение

Решение:

. Разделив обе части на , получим . Проинтегрируем полученное уравнение . Представим , как , тогда

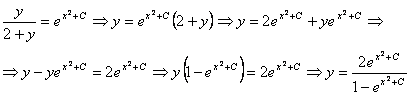
Ответ:

Решением данного уравнения является .

Задание №18. Вопрос №9.

Найти общее решение уравнения:

Решение:

Найдем корни характеристического уравнения: , тогда , следовательно , , тогда

фундаментальную систему решений образуют функции:

,

Т.к. действительные и мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решений и , возьмем , , тогда общее решение однородного уравнения будет иметь вид:

Представим правую часть уравнения, как и сравним с выражением, задающим правую часть специального вида:

. Имеем , , тогда т.к. - многочлен второй степени, то общий вид правой части: . Найдем частные решения:

, ,

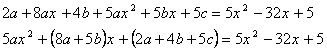
Сравним коэффициенты при 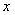слева и справа, найдем , решив систему:

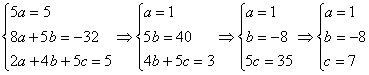, отсюда .

Тогда общее решение заданного неоднородного линейного уравнения имеет вид: .

Ответ:

.

Дополнительно Часть I.

Задание №7. Вопрос №1.

Найти предел: .

Решение:

.

Ответ:

Заданный предел равен .

Задание №9. Вопрос №8.

Найдите уравнение асимптот и постройте их графики:

.

Решение:

1. Область определения данной функции: .

2. Т.к. точка не входят в область значений функции, то это точка разрыва, а т.к. 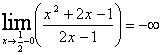и 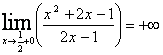, следовательно, уравнение – уравнение вертикальной асимптоты.

3. Уравнения правой и левой наклонных асимптот имеют вид: , где:

т.к. правая и левая наклонные асимптоты совпадают, то уравнение наклонной

асимптоты имеет вид: .

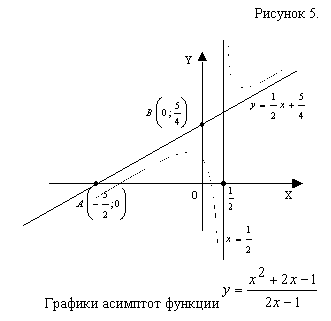
Для построения графиков асимптот (см. рис. 5), найдем

точки пересечения наклонной асимптоты с осями

координат:

С осью OX: точка,

с осью OY: точка

Ответ:

и – уравнения асимптот заданной функции.

Задание №11. Вопрос №6.

Исходя из определения производной, докажите: 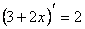.