Гамма функции
Страница 2
12
сходится равномерно на каждом сегменте  ,
,  . Выберем число
. Выберем число так , чтобы
так , чтобы  ; тогда
; тогда  при
при  .Поэтому существует число
.Поэтому существует число  такое , что
такое , что  и
и  на
на .Но тогда на
.Но тогда на  справедливо неравенство
справедливо неравенство

и так как интеграл  сходится, то интеграл
сходится, то интеграл  сходится равномерно относительно
сходится равномерно относительно 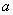 на
на  . Аналогично для
. Аналогично для  существует такое число
существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  . При таких
. При таких  и всех
и всех  получим
получим  , откуда в силу признака сравнения следует , что интеграл
, откуда в силу признака сравнения следует , что интеграл  сходится равномерно относительно
сходится равномерно относительно 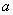 на
на  . Наконец , интеграл
. Наконец , интеграл

в котором подынтегральная функция непрерывна в области
 , очевидно, сходится равномерно относительно
, очевидно, сходится равномерно относительно 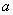 на
на  . Таким образом , на
. Таким образом , на  интеграл
интеграл

13
сходится равномерно , а, следовательно , гаммма функция бесконечно дифференцируема при любом 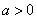 и справедливо равенство
и справедливо равенство

 .
.
Относительно интеграла  можна повторить теже рассуждения и заключить, что
можна повторить теже рассуждения и заключить, что

По индукции доказывается , что Г-функция бесконечно дифференцируема при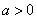 и для ее я
и для ее я  -ой производной справедливо равенство
-ой производной справедливо равенство

Изучим теперь поведение  - функции и построим єскиз ее графика .
- функции и построим єскиз ее графика .
Из выражения для второй производной  -функции видно, что
-функции видно, что  для всех
для всех 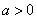 . Следовательно,
. Следовательно,  возрастает. Поскольку
возрастает. Поскольку  , то по теореме Роля на сегменте [1,2]производная
, то по теореме Роля на сегменте [1,2]производная  при
при  и
и при
при  , т. е. Монотонно убывает на
, т. е. Монотонно убывает на  и монотонно возрастает на
и монотонно возрастает на  . Далее , поскольку
. Далее , поскольку  , то
, то  при
при  . При
. При  из формулы
из формулы  следует , что
следует , что  при
при  .
.
14
Равенство  , справедливое при
, справедливое при 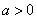 , можно использовать при распространении
, можно использовать при распространении  - функции на отрицательное значение
- функции на отрицательное значение 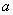 .
.
Положим для , что
, что  . Правая часть этого равенства определена для
. Правая часть этого равенства определена для 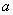 из (-1,0). Получаем, что так продолженная функция
из (-1,0). Получаем, что так продолженная функция  принимает на (-1,0) отрицательные значения и при
принимает на (-1,0) отрицательные значения и при  , а также при
, а также при  функция
функция  .
.
Определив таким образом  на
на  , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
, мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением  окажется функция, принимающая положительные значения и такая, что
окажется функция, принимающая положительные значения и такая, что 

 при
при  и
и  . Продолжая этот процесс, определим функцию
. Продолжая этот процесс, определим функцию  , имеющею разрывы в целочисленных точках
, имеющею разрывы в целочисленных точках  (см. рис.1)
(см. рис.1)
Отметим еще раз, что интеграл

определяет Г-функцию только при положительных значениях 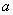 , продолжение на отрицательные значения
, продолжение на отрицательные значения 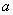 осуществлено нами формально с помощью формулы приведения
осуществлено нами формально с помощью формулы приведения 
 .
.
15

(рис.1)
4. Вычисление некоторых интегралов. 16
Формула Стирлинга
Применим гамма функцию к вычислению интеграла:
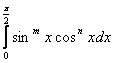
где m > -1,n > -1.Полагая , что  ,имеем
,имеем