Исследования остатков е, предполагают проверку наличия следующих пяти предпосылок МНК[1]:

• случайный характер остатков;
• нулевая средняя величина остатков, не зависящая от х,-;
• гомоскедастичность — дисперсия каждого отклонения Е, одинакова для всех значений х;
• отсутствие автокорреляции остатков. Значения остатков е7 распределены независимо друг от друга;
• остатки подчиняются нормальному распределению.

В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и по методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков е, не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS — Ordinary Least Squares) заменять обобщенным методом, млн. е. методом GLS (Generalized Least Squares).

Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии.

Статистическая надежность регрессионного уравнения в целом оценивается на основе F-критерия Фишера: проверяется нулевая гипотеза о несоответствии представленных регрессионным уравнением связей реально существующим (H₀: a₀= a₁=a₂=…=a_m=0, R=0). Для проверки H₀ следует рассчитать значение F-критерия (F_р) и сравнить его с табличным значением (F_т), определяемым с использованием таблиц по заданным уровню значимости (a= 05) и числу степеней свободы (d.f.1 = m-1 и d.f.2 = n-m). F_р определяется из соотношения факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле:

,

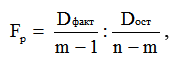где D_факт, D_ост – суммы квадратов отклонений, характеризующие факторную и остаточную вариации результативного признака. В случае однофакторного дисперсионного комплекса D_факт и D_ост выражаются в соответствии с (2.11),

d.f.1 = m-1 – число степеней свободы факторной дисперсии,

d.f.2 = n-m – число степеней свободы остаточной дисперсии.

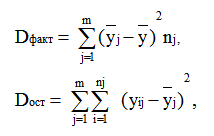
где y_ij, – значения результативного признака у i–й единицы в j–й группе,

i – номер единицы совокупности,

j – номер группы,

n_j – численность j–й группы,

– средняя величина результативного признака в j–й группе,

– общая средняя результативного признака.

Если F_р > F_т, то гипотеза H₀ отвергается. При этом с вероятностью 1-a = 0,95, или 95%, принимается альтернативная гипотеза о неслучайной природе оцениваемых характеристик, т.е. признается статистическая значимость регрессионного уравнения и его параметров.

[1] Статистическое моделирование и прогнозирование: Учеб. пособие / Под ред. А. Г. Гранберга. — М.: Финансы и статистика, . 1990.-С. 158.