Е. И. Мещерякова, Воронежский институт МВД России
Для количественного измерения результатов использования различных систем обучения нами разработаны математические модели, в частности, модель интегрального показателя использования различных систем обучения юридическим дисциплинам и модель оценки способности курсантов выбирать правильные решения при выполнении тестовых заданий в процессе осуществления контроля.
Модель итогового интегрального показателя применения определенной системы обучения выглядит следующим образом:

Здесь система количественных характеристик результата обучения представлена с помощью nмерного вектора X (в качестве элементов системы можно рассматривать, например, средний балл текущего, рубежного или итогового контроля, экспертные оценки уровня развития способности к самоорганизации, степени интенсивности обучения, мотивации самостоятельной деятельности и многие другие). Значимость каждого показателя, входящего в эту систему, задается весовыми коэффициентами, система которых обозначена W и для n результирующих показателей выглядит как диагональная матрица. Систему показателей, характеризующих затраты времени преподавателя для осуществления им определенных действий, связанных с разработкой и применением либо только с применением системы обучения, обозначим с помощью m-мерного вектора U. Если учесть, что при максимизации интегрального показателя результатов применения системы обучения целесообразно делать это с минимальными затратами времени преподавателя, то вектор будет включать в качестве элементов t 1 j . Каждой из составляющих затрат времени преподавателя присваиваем весовой коэффициент, исчисленный с помощью экспертных оценок, и обозначаем систему таких коэффициентов Q, а система таких коэффициентов приобретает вид диагональной матрицы. Тогда первое слагаемой формулы учитывает только те характеристики, которые непосредственно связаны с управлением учебной и познавательной деятельностью курсантов в процессе изучения ими юридической дисциплины с применением определенной системы обучения, а второе слагаемое - затраты времени преподавателя на разработку системы, ее методического обеспечения и совершенствования в процессе применения.
Изменяя значения весовых коэффициентов, можно найти такое значение интегрального показателя, которое обеспечивает самые высокие при заданных условиях результаты обучения. Если же при одинаковых весовых коэффициентах определить результаты в соответствии с количественными оценками составляющих таких результатов, то можно судить о величине интегрального показателя применения конкретной системы обучения.
Мы проводили расчеты интегральных показателей перед началом и по окончании семестра после завершения эксперимента по применению креативно - акцентной системы обучения. В качестве показателей, учитываемых для характеристики результатов процесса обучения с применением традиционной (1 поток, 1 группа) и креативно - акцентной (2 поток, 4 группа) систем обучения использовались следующие: уровень успеваемости (средний балл), способности применять полученные знания для анализа конкретных ситуаций, соотношение между производительным и непроизводительным временем самостоятельной подготовки, повышение ответственности за результаты обучения, уровень информационный культуры, укрепление убежденности в правильности выбора профессии, сформированность правового мировоззрения. Только первый из указанных показателей имеет фиксированную количественную оценку, все остальные количественные оценки определялись на основе мнений экспертов о степени значимости соответствующей результирующей характеристики. Степень согласованности мнений экспертов определена с помощью рассчитанного нами коэффициента конкордации, величина которого, оцененная по критерию х2 позволяет утверждать, что мнения экспертов согласованы и в них прослеживается закономерность. По результатам расчетов значения интегральных коэффициентов соответственно составили: в 1 группе перед началом изучения финансового права 353,33 единицы, после изучения - 396,94 единицы; в 4 группе - 495,9 единицы и 550,74 единицы соответственно. Это означает, что применение креативно - акцентной системы обучения привело к более высоким результатам, обеспечило более высокую эффективность обучения. Обращает на себя внимание и то обстоятельство, что интегральный показатель возрос в контрольной группе на 28,41 единицы, в экспериментальной - на 86,26 единицы.
Особый интерес представляет построение математических моделей для описания развития творческих способностей в связи с применением конкретных систем обучения. Вряд ли возможно построение математической модели, которая отразила бы все составляющие сложнейшего процесса управления развитием креативных способностей, ведь и процесс, и способности не поддаются количественной оценке. Однако некоторые их составляющие, по нашему мнению, поддаются математическому моделированию. Мы представили с помощью модели оценку способности выбирать правильное решение при выполнении тестовых заданий. Тестовые задания строились таким образом, что позволяли оценить как знания дефиниций, так и способности творчески осмысливать знакомые, малознакомые и незнакомые ситуации, задаваемые тестом.
В разработке представляемой модели мы использовали общие подходы Р. Аткинсона, предложенные им для процесса поиска и принятия решений при опознании1. В нашей модели процесс оценки тестовых ситуаций и выбора варианта ответа испытуемыми (курсантами, слушателями) рассматривается как вероятностный и исследован методами теории вероятностей, которые применялись для оценки уровня сформированности творческих способностей субъектов, изучивших юридическую дисциплину без применения и с применением креативно - акцентной системы обучения. Критерий - время выбора правильного варианта в тестовых заданиях различной сложности. Сложность тестового задания определялась тем, насколько знаком испытуемому правильный ответ - содержится ли он в его памяти как результат изучения дисциплины или требует поиска путем сопоставления понятий, размышления и осуществления иных мыслительных действий.
Мы обозначили группу тестов с правильными положительными ответами Р, а группу тестов с правильными отрицательными ответами N. В группу с правильными положительными ответами включили те, для выбора которых достаточно помнить правильные определения понятий и нормативных источников, в группе тестовых заданий с правильными отрицательными ответами выделили соответственно сложности заданий три подгруппы:
N(1), N(2), N(3).
Модель математического ожидания правильного ответа выглядит следующим образом:
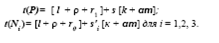
Здесь l - время, необходимое для изучения курсантом тестового задания и его понимания; ρ — время принятия решения об осуществлении ответа, основанного только на запоминании изученного материала, которое берется с весом, равным его вероятности; k + αm - время, необходимое для поиска ответов на тестовые задания, в которых требуется не только вспомнить, но и проанализировать ситуации, также взятое с весом, равным его вероятности; r0, r1 - время осуществления ответа на вопросы первой и второй групп тестов соответ - -1 ственно;
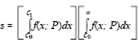
для груп - пы тестов с правильными положительными отве - тами и
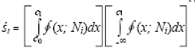
для группы тес - тов с правильными отрицательными ответами. Величины śi и s определяются соответствующими функциями распределения знакомости курсантам информации, содержащейся в тестовом задании, значениями с0, с1 и не зависят от m, a t(Ni)и t(P), построенные как функции m, представляют собой прямые, наклон которых определяется соответственно αs'i и αs.
Полученные в процессе наблюдения данные о времени выбора правильных ответов, а также осуществление расчетов с помощью приведенных при описании модели формул позволили получить результаты, представленные графически на рис.1. Здесь сплошными и пунктирными линиями показаны прямые, характеризующие показатели времени правильных ответов для экспериментальной и контрольной групп соответственно, они обозначены:
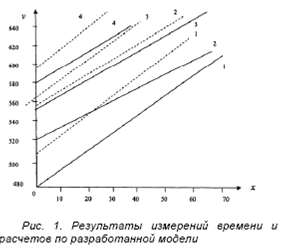
1 – для подгруппы вопросов, на которые правильным является положительный ответ, 2,3,4, - для подгрупп вопросов, на который правильным является отрицательный ответ. Как видно, время выбора правильного варианта ответа по всем подгруппам вопросов меньше у конкурсантов, изучающих дисциплину в примене - нием креативно – акцентной системы обучения, хотя различия во времени по подгруппам неодинаковы, о чем свидетельствуют различные углы наклона прямых и расстояния между прямыми, отражающими математические ожидания времени выбора правильных ответов по соответствующим подгруппам вопросов.
|