Глава III
Первичное измерение(квантификация) социальных характеристик

Мы уже знаем, что, поскольку социолог имеет дело с массовыми процессами, он по необходимости оперирует различными числовыми показателями, выражающими частоты, протяженности и напряженность связи между различными социальными характеристиками. Предпосылка всех операций с количественными выражениями свойств социальных объектов и процессов — первичное измерение качественных признаков или их квантификация. Любое измерение начинается с поиска простейших качественных признаков, отношения между которыми могли бы быть выражены в некотором числовом масштабе.

Измерение — это процедура, с помощью которой измеряемый объект сравнивается с некоторым эталоном и получает числовое выражение в определенном масштабе или шкале.

Измерением называют также однозначное отображение эмпирической системы с отношениями между ее элементами (составляющими, состояниями, свойствами и т. д.) в числовую систему с соответствующими отношениями между числами. В итоге формируется числовая модель измеряемого объекта, а точнее — некоторых выделенных в качественном анализе его сторон. Поскольку получить точный аналог (изоморфную модель) практически не удается, разрабатывают приблизительный аналог (гомоморфную модель), в числовом выражении условно соответствующий оригиналу. Социальные измерения часто называют квалиметрическими, т.е. условно количественными аналогами качественных отношений.

Проблема первичного измерения — лишь частично математическая. Чтобы по определенным правилам приписать числа свойствам социального объекта, надо обстоятельно уяснить их. содержательную структуру и найти соответствие между нею и инструментом измерения, т. е. это задачи качественно-количественного анализа.

В принципе изменению подлежат любые свойства социальных объектов: качественные и количественные. С количественными (такими, как возраст в числе исполнившихся лет, заработок в денежных единицах, образование в годах обучения и т. п.) дело обстоит сравнительно просто. Для них уже есть общепринятые эталоны измерения: один год для возраста или образовательной подготовки, один рубль для исчисления заработка, один человек для исчисления размера семьи.

Качественные характеристики (социальная принадлежность, мнения людей и т. п.) не имеют установленных эталонов измерения. 1

• 1 Подробнее о процедурах измерения социальных характеристик см.: Толстова Ю. Н. Измерение в социологии. М., 1997 (в печати), о также: [68; 112; 215; 232; 333] и в прил. 2 — "Аннотированный список".

Их приходится конструировать в соответствии с природой изучаемого объекта и согласно гипотезам исследования. Поэтому мерительные процедуры качественных характеристик—своего рода изобретения, которые, однако, осуществляются по определенным типовым способам. О них мы и будем говорить далее.

В первом приближении способы измерений в социологии можно разделить на две категории.

Первую составляют приемы, с помощью которых измеряются количественные признаки объектов с точки зрения их физического пребывания в пространстве и времени.

Протяженность в пространстве может быть использована как мера удаленности людей от индустриально-культурного, политического центра в исследованиях политических движений. Физическая протяженность коммуникаций между взаимодействующими людьми характеризует одно из условий их совместной деятельности. Число строк в тексте, содержащее определенную мысль, используется как мера для классификации текстов по частоте повторения данной мысли (или упоминаемых событий).

Единицы протяженности во времени — частота событий, их длительность, величина временных интервалов — также характеризуют социальные процессы с количественной стороны. Во всех этих случаях пригодны "естественные" эталоны измерения.

Вторая категория измерений относится к объектам, для которых не существует общепринятых шкал. Но даже самые сложные социальные явления могут быть квантифицированы со стороны их протяженности, интенсивности, частоты повторяемости. Онтологическое основание такого утверждения — качествен но-количественная определенность любых объектов реальной действительности, каковая характеризуется в философской категории меры. Что же касается практических возможностей измерений, то они целиком зависят от нашего умения найти или изобрести надежную измерительную процедуру.

1. Конструирование эталона измерения — шкалы

Рассмотрим некоторые общие правила первичной измерительной процедуры и способов проверки этой процедуры на надежность. 2

• 2 Подчеркнем, что в этойтлаве мы рассматриваем основные требования к простейшей первичной квалтификации отдельных свойств, сторон социальных объектов. В более полном виде измеряемые объекты находят отображение в достаточно сложной формализированной системе. Это предполагает измерение многих свойств и создание своего Рода моделей объектов и процессов в виде специальных качественно-количественных показателей-индексов, многомерных классификаций, типологических конструкций и т. д. (см. гл. 5, § 1 и 2).

Поиск эталона измерения

Нахождение эталона измерения осуществляется в четыре стадии, каждая из которых — необходимая предпосылка надежности будущей шкалы.

Первая стадия — качественная классификация объектов. Собираясь, например, измерять структуру ценностных ориентации или социальных установок личности, мы прежде всего должны четко классифицировать типы ориентации, исходя из теоретической концепции и задач исследования. Можно положить в основу классификации иерархию потребностей или интересов, сфер деятельности, социальные функции, социальные ситуации, которые бы различались по степени свободы выбора целей и средств деятельности и т. д.

Вторая стадия — поиск протяженности выделенных в качественном анализе свойств. Следует установить, обладают ли эти свойства прерывной или непрерывной протяженностью, можно ли их представить в виде различных последовательных состояний измеряемого качества.

Рассмотрим с этой точки зрения какую-нибудь ценностную ориентацию (на материальный достаток, культурные ценности, творчество и др.)- Ее можно "вытянуть" в несколько протяженностей — континуумов. Один континуум составляет: сильная—средняя—слабая ориентации; другой: устойчивая—малоустойчивая— неустойчивая; третий: господствующая—рядоположен-ная—подавленная; четвертый: центральная или периферийная. В зависимости от концепции исследования можно выделить и другие протяженности.

Третья стадия — установление эмпирических индикаторов или внешних признаков тех свойств объекта, которые поддаются расположению в континуум.

Индикатор — внешне хорошо различимый показатель измеряемого признака. С его помощью устанавливается наличие или отсутствие признака, его состояние.

Например, высота ртутного столбика термометра — индикатор температуры.

Простейший индикатор расположения какого-то объекта среди других объектов ориентации — порядковое место, отмечаемое опрашиваемым в заданном списке. Например, из 18 объектов он помечает объект М порядковым номером 1. Этот номер — индикатор доминирования объекта М с точки зрения интересов субъекта. Объект N , помеченный порядковым номером 18, будет располагаться в конце протяженности ("подавленная ориентация на N ").

Сложнее найти индикатор для протяженности по критерию "сильные", "средние", "слабые" ориентации. Один из возможных вариантов таков.

Испытуемым предлагают три ситуации, в которых они принимают решение о выборе "ценностного ориентира". Ситуации различаются по степени свободы выбора. Допустим, измерению подлежат интересы к различным видам занятий в сфере досуга. Предлагаются три одинаковых списка возможных занятий, число которых в каждом списке 18 (чтение художественной литературы, посещение гостей, просмотр телепередач и т. д.).

В первой ситуации (широкий диапазон выбора) испытуемый имеет право без ограничения указать любые занятия, которые ему нравятся. Во второй ситуации (средний диапазон выбора) он оставляет в списке лишь шесть наиболее важных для него занятий, в третьем случае (узкий диапазон) — не более трех, для него особенно значимых.

Индикатор "сильной" ориентации — выбор данного занятия —имел место во всех трех ситуациях; "средний" — выбор в первой и второй ситуациях; "слабый" — выбор имел место только при широком диапазоне принятия решения.

Одно и то же свойство можно фиксировать с помощью нескольких индикаторов, которые сводятся в общий показатель — индекс. Это случай сложного первичного измерения, по технике напоминающего приемы вторичных измерений. Так, для определения интенсивности интереса к какому-то виду досуга можно использовать и саморанжирование занятий (первый пример), и выборы в нескольких ситуациях, и оценки занятий по десятибалльной системе, и другие способы. 3

• 3 Детально эти процедуры рассматриваются Г. И. Саганенко [232; 233. Разд. 4.2].

Наиболее надежный индикатор будет получен по совмещению нескольких способов: некоторая группа занятий помечена первыми номерами по ранжированному списку, она же выбрана в трех названных выше ситуациях, эти занятия были оценены 10 баллами при максимуме 10 и минимуме 1. Такой сводный числовой показатель и называют индексом.

Четвертая стадия заключается в том, чтобы уяснить, все ли единицы, составляющие измеряемый объект, укладываются в ранжируемый ряд, все ли они обладают свойством занимать определенное место в континууме отношений по принятым индикаторам.

Например, в одном из наших исследований индикатором отношения к труду рабочих был показатель нормы выработки (значительно перевыполняет норму — перевыполняет — выполняет — не выполняет норму). Однако он был неудачным, так как применим не ко всем рабочим, а только к "сдельщикам". Труд тех, кто получает повременную оплату, оценивается по другим показателям: качеству работы прежде всего. Например, чем меньше времени тратит ремонтник на устранение текущих неполадок, тем выше качество профилактического ремонта.

В итоге описанных выше операций устанавливается эталон, или шкала измерения.

Отношения между пунктами шкалы должны отображать отношение свойств объекта в понятиях "равно", "больше", "меньше". В нашем примере с ценностными ориентациями отношениям "сильная">"средняя">"слабая" соответствуют отношения трех пунктов построенной шкалы: (выбор сделан в трех ситуациях) > (выбор сделан в первой и второй ситуациях) > (выбор сделан только в первой ситуации). Теперь предстоит испытать шкалу на надежность.

Способы проверки процедуры первичного измерения на надежность

Следует иметь в виду, что операции повышения надежности первичного измерения, которые мы будем здесь рассматривать, используются лишь на стадии отработки инструмента измерения в процессе пилотажа. После окончательной проверки надежности построенных шкал и сбора данных на объектах исследования акцент контроля их достоверности переносится с первичного измерения на вторичные, т. е. комбинаторные процедуры, и так последовательно вплоть до обоснования достоверности итоговых выводов.

В целом же достоверность результатов исследования зависит от многих составляющих, начиная с того, насколько обоснована его общая концепция и все компоненты теоретико-методологического раздела программы, а далее — от качества исходных данных, системы их отбора, т. е. соответствия типа выборки (и ее организации) целям исследования, качества анализа данных и, наконец, от глубины интерпретации полученных зависимостей и связей. 4

• 4 О требованиях и операциях, необходимых для гарантии общей Достоверности данных, см. [68, 200, 233]. Если учесть все возможные ошибки, связанные с неполным соответствием теоретической модели объекта самому объекту, возможными упущениями на разных этапах исследования (например, при расчетах выборки, тиражирования полевых документов и т. д.), спецификой типов возможных ошибок (напри-Мер, систематические или случайные), а также некоторые другие причины, то, как показал Б. 3. Докторов [68], в так называемой метрологической карте можно обнаружить 162 ( I ) составляющие возможных ошибок.

К сожалению, нет единообразия в толковании термина "надежность" применительно к социологической информации. Главная причина состоит в том, что одни авторы трактуют надежность слишком расширительно как качество всего исследования и, следовательно, его итогов, а другие, напротив, отождествляют надежность с тем или иным особым ее проявлением (например, с.устойчивостью данных, их адекватностью целям исследования и т. д.).

Не останавливаясь здесь на дискуссии терминологического характера, заметим, что в строгом смысле слова понятие надежности измерения правомерно относить именно к инструменту, с помощью которого производится измерение, но не к самим данным, подлежащим измерению, В отношении данных, как и заключительных выводов из исследования, правильнее говорить, что они достоверны (или относительно достоверны) в том числе и потому, что фиксированы надежным инструментом.

Возможны различные типологии приемов оценки надежности первичной информации, например, с точки зрения внешнего или внутреннего контроля данных, получаемых определенным способом. Мы будем пользоваться обобщающим понятием надежности инструмента измерения (и соответственно надежности данных, фиксируемых этим инструментом), имея в виду три составляющие: (1) обоснованность, (2) устойчивость и (3) правильность измерения. Естественно, что и методы контроля на надежность нужно рассматривать в этих трех аспектах 5 .

• 5 Наиболее детально методы и техника контроля данных на надежность изложены в работах Г. И. Саганенко [233] и В. И. Папиотто [200]. Последний применяет аналитический подход к предмету, выделяя множество разновидностей надежности и технических приемов оценки ее уровня [200. С. 74—75], тогда как Саганоцко, ряд идей и примеров из книги которой мы используем, акцентирует внимание на наиболее существенных, непременных требованиях и сравнительно простых способах контроля надежности.

Обоснованность 6 шкалы заключается в том, что с ее помощью целенаправленно измеряют вполне определенное свойство или признак, не смешивая его с другими.

• 6 В зарубежной и отечественной (особенно в психологической) литературе вместо термина "обоснованность" часто используется как его аналог понятие "валидность". Однако в английском " reliability " (обоснованность) подчеркивает возможность полагаться на кого-либо, в данном случае доверять полученной информации благодаря тому, что она адекватна объекту измерения [337. С, 132—138], a " validity " семантически имеет оттенок устойчивости, "прочности" полученной информации. Поэтому термин "валидность" правильнее было бы соотносить ве с обоснованностью, во с устойчивостью данных измерения.

Предположим, при опросе телезрителей им предлагают указать, каким из перечисленных в прилагаемом списке передачам телевидение уделяет "слишком много", "достаточно" и "слишком мало" времени. Если с помощью этой трехчленной шкалы исследователь намерен фиксировать среднее время, отводимое телепередачам, его измерение будет необоснованным. В действительности он измеряет отношение людей к данным передачам, а не объем времени, отводимого для их трансляции. Обоснованное измерение объема времени на передачи разного типа — документальный анализ "сетки" программ телевидения.

Чтобы повысить обоснованность измерения, используют ряд технических приемов.

(1) Наиболее простой способ — логические рассуждения на основе опыта и здравого смысла.

Обратимся к примеру из обследования, проведенного Б. М. Фирсовым. Задача: определить среднюю интенсивность просмотра телепередач путем массового опроса телезрителей.

Первый вариант построения шкалы был таков. Вопрос: "Сколько приблизительно часов в день Вы проводите у телевизора?" Шкала для ответа содержала пять интервалов: (не больше 1 часа) — (от 1 до 2 часов) — (от 2 до 3 часов) — (от 3 до 4 часов) — (свыше 4 часов).

Путем логических рассуждений были высказаны следующие сомнения в обоснованности такого метода. Следует ука зать день просмотра телепередач: будний, субботний или воскресный. Иначе неясно, какой из дней зритель выберет за эталон оценки. Не спасет положения и вопрос, сколько в среднем часов в неделю зритель проводит у телевизора, так как люди не привыкли думать в "средних" величинах.

Значит, надо поставить вопрос так, чтобы: а) выделить дни недели и б) указать понятный для зрителя эталон оценки. Поэтому более удачный вариант построения шкалы для решения той же задачи следующий [274. С. 142].

Первый вопрос: "Сколько дней в неделю Вы, как правило, смотрите телевизионные передачи?":

1. почти все дни недели;
2. 3 или 4 дня в неделю;
3. 1 или 2 дня в неделю;
4. меньше, чем один раз в педелю, т. е. не каждую неделю;
5. в сущности, совсем не смотрю.

Второй вопрос: "Не могли бы Вы приблизительно оценить, сколько в среднем часов Вы проводите у телевизора в тот день, когда смотрите передачи?" Сделайте отметку в каждой строке.

Дни недели	Время просмотра
	не больше 1 часа	от 1 до 2 часов	от 2 до 3 часов	от 3 до 4 часов	свыше 4 часов
В будние дни	—	—	—	—	—
В субботу	—	—	—	—	_
В воскресенье	_	-	—	—	—

Теперь, пользуясь простыми арифметическими действиями, можно рассчитать "среднепросмотровое" время за неделю и составить шкалу.

Обозначим а число дней в неделю, уделяемых просмотру телепередач. Числовые индикаторы ответов на первый вопрос взяты как средние эмпирически полученных интервалов (в числе дней просмотра), а именно: 6; 3,5; 1,5; 0,7; 0. Обозначим Ъ количество часов, затраченных на просмотр телепрограмм в определенные дни (ответы на второй вопрос) также по средним: 4,5; 3,5; 2,5; 1,5; 1.

Обозначив будние дни как d , субботние s , воскресные w , рассчитаем среднепросмотровое время за неделю Т:

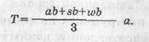
Для телезрителя, который в ответе на первый вопрос пометил "3 или 4 раза в неделю", в ответе на второй указал "до 1 часа в будни" и "от 2 до 3 часов в субботу и воскресенье" среднепросмотровое время исчисляется по формуле:

Неадекватное понимание того, что же мы измеряем, может привести к серьезным последствиям. Поучительный пример: дискуссия в прессе относительно добросовестности служб общественного мнения в опросах о рейтинге политических деятелей.

В ноябре 1997 г. два ведущих российских центра изучения общественного мнения представили данные общероссийских опросов. Рейтинги Президента, премьера и некоторых других ключевых фигур в правительстве по опросам центра "А" на 10—12% отличались от рейтингов по опросам службы "Б". Это вызвало публичный скандал: одна служба подыгрывает правительству, а другая — оппозиции. Что же в действительности случилось? Служба "А" задавала вопрос "Одобряете ли Вы деятельность..?", а служба "Б" предлагала формулировку "Доверяете ли Вы..?". На протяжении трех месяцев все показатели доверия/недоверия на 10—12% уступали показателям одобрения/неодобрения, причем этот разрыв устойчиво сохранялся в отношении Президента и премьера, но сильно колебался в отношении ряда других правительственных чиновников (т. е. граждане сформировали позицию относительно Президента и премьера, но не имели четкой позиции в отношении Других, неключевых фигур в правительстве). Через две недели после этого скандала служба "Б" в общероссийском опросе предложила респондентам обе формулировки в одном интервью. Обнаружилось, что доверяют правительству 14-16% опрошенных, но одобряют его деятельность в той же выборке 29%. Логика здесь такая: "Я могу не очень доверять искренности намерений правительства, но то, что оно делает, я склонен сейчас одобрить".

Заметим, однако, что логические рассуждения, наподобие приведенных выше, повышают обоснованность, но не яв ляются прямым доказательством того, что мы меряем искомое свойство.

(2) Тест по "эталонной гр ynne " - более сильный прием проверки инструмента на обоснованность. Смысл проверки — в сопоставлении данных, полученных путем измерения по шкале, с достоверными сведениями об объекте измерения.

Так, шкала на отношение к соблюдению норм права может быть обоснована опросом осужденных правонарушителей (они рассматриваются как "эталон" негативного полюса шкалы), в сравнении с "эталонной" группой законопослушных граждан. Дихотомизация полярных групп по шкале должна созпадать с фактической поляризацией эталонных групп в пределах допустимой ошибки, величина которой зависит от задач исследования.

(3) Поиск независимого критерия как разновидность внешнего контроля надежности для измерения того же самого объекта или свойства.

Если подключить к телевизионному приемнику прибор, регистрирующий время его работы, и сопоставить показания прибора с результатами опроса о частоте и длительности просмотра телепрограмм, можно точно установить обоснованность данных опроса.

Не имея такой возможности, Б. М. Фирсов сопоставлял сведения, полученные по шкале среднепросмотрового времени, с данными по другой шкале, названной "изменение привычек" (табл. 1) [274, С, 107]. Последняя конструировалась по ответам на вопрос: "Придется ли Вам в случае длительного отсутствия телевизора менять свои привычки, способ проведения досуга, жизненный уклад?" Берем два крайних варианта ответов по второй шкале, отбрасывая промежуточные (в процентах к численности представителей каждого типа, т. е. по строке). Очевидно, что шкала "увлеченности", полученная как вторичная группировка данных среднепросмотрового времени Т, высоко согласуется со шкалой "привычек" и, следовательно, может считаться вполне обоснованной. 7

• 7 Пользуясь той же шкалой, автор провел повторное сравнительное исследование аналогичной выборки ленинградцев спустя 10 и 12 лет. За период с 1967 г. по 1979 г. обнаружилось, что доля "весьма умеренных" телезрителей упала с 32% до 6% и "весьма увлеченных" повысилась с 16% до 40% [157. С. 701].

Таблица 1
Обоснование шкалы увлеченности телевидением по независимому критерию

Шкала "увлеченности" по средне-просмотровому времени в неделю	Шкала "изменения привычек"
"Думаю, что придется изменить привычки"	"В моей жизни ничего не изменится" + "Вряд ли что изменится в моей жизни"
T 1 — "Весьма умеренные" (до 3 ч.)	15,8	11,7+34,4-46,1
T 2 — "Умеренные" (от 3 до 10 ч.)	36,1	6,0+31,3-37,3
Т 3 — "Увлеченные" (от 10 до 15 ч.)	48,7	5,5+22,9=28,4
Т 4 — "Весьма увлеченные" (от 15 до 17 ч.)	60,0	1,6+17,0-18,6

(4) Использование метода судей для отбора пунктов шкалы. Сомнения в обоснованности возникают уже на стадии первоначального отбора пунктов шкалы. В каких единицах считать время просмотра телепередач? В днях, часах, в частоте просмотров? Какие понятия выбрать для построения шкалы?

Эти вопросы лучше всего доверить решению компетентных судей. В нашем случае ими являются типичные телезрители» которые будут представлять как бы микромодель основной массы опрашиваемых. В этом смысле "судейство" как способ контроля обоснованности шкалы надо отличать от опроса экспертов — профессиональных специалистов в данной области.

Численность судей зависит от меры однородности или разнородности выборочной совокупности основного обследования. Так, при построении шкал на отношение к досуговым занятиям мнения мужчин и женщин об одних и тех же занятиях будут существенно разными. Рекомендуется отобрать для судейства половину судей из женщин, половину — из мужчин. Не меньшее значение в данном случае будут иметь уровень образования и род занятий. Для компоновки судейской группы используют метод квоты, т. е. устанавливают пропорции судей по набору существенных признаков, включая, например, пол, возраст, образование, выражающих позиции разных групп респондентов в предполагаемой выборке. 8

О квотировании выборки см. на с. 349.

(5) Один из широко используемых приемов внутреннего контроля обоснованности — совмещение нескольких показателей для регистрации определенного одного свойства, или построение индекса. Типы индексов крайне разнообразны. Они широко используются в психологических тестах, в социально-экономических исследованиях. Суть индексной обоснованности в том, что, согласно гипотезе, данному свойству находится множество его проявлений, для каждого из которых формируют отдельную шкалу. Затем измерения по частным шкалам либо суммируются, либо из них образуют логические конструкции, как это было сделано в показателе "логический квадрат" для построения производной шкалы удовлетворенности работой (см. с. 261).

Вполне справедливо выделяют два существенно разных аспекта обоснованности: теоретический и эмпирический. Первый непосредственно связан с содержательными посылками исследования и предполагает установление значимых связей с широким классом ситуаций, предсказываемых теорией, второй требует доказательства надежной регистрации данных в сравнительно узком секторе, в частном проявлении изучаемых объектов. "Если валидность (синоним обоснованности. — Е.Я.) эмпирическую через измерение обеспечивают, — (включает В. И. Паниотто, — то валидность теоретическую только проверяют, т. е. уточняют область валидности методики, границы интерпретации получаемых материалов" [200. С. 109].

Устойчивость измерения выражается в однозначности информации, которую мы извлекаем с помощью данной процедуры. Нередко устойчивость ошибочно отождествляют с надежностью процедуры в целом. И хотя последняя зависит не только от устойчивости, но также от обоснованности и правильности операций, подобное смешение не случайно: проверка инструмента на устойчивость — важнейшее условие его надежности.

1) Наиболее распространенный прием контроля на устойчивость — повторное измерение. Один и тот же объект измеряется дважды с двух-трехнедельным временным интервалом и с помощью одинаковой процедуры. Шкала считается устойчивой, если совпадения между первой и второй сериями измерений будут достаточно высокими.

В отличие от проверки на устойчивость измерения физических объектов социолог или психолог сталкивается здесь с особой проблемой — влиянием психологической установки человека, возникающей после первого замера. Люди могут намеренно или непроизвольно подгонять данные второго замера к предыдущим. Или же, напротив, интуитивно сопротивляясь повторному эксперименту, они покажут новые результаты.

Таблица 2
Сравнение данных двух последовательных замеров: оценка совпадения (+) и несовпадения (—) результатов в дихотомической шкале

Пункты шкалы	Обследуемые всего, N-50 чел.				Итог по строке
А	В	В	Г	...n	(+)	(-)	% совпадений
1	+	+	-	+	+	45	5	90
2	+	-	+	+	+	44	б	88
3	-	+	-	-	-	25	25	50
4	+	+	+	-	+	42	8	84
Б	+	+	+	-	+	46	4	92
в	+	+	-	+	+	41	9	82
15	+	+	-	+	+	45	5	90
Итог по ( + ) колонке ( - )	141	141	96	10 5	13 2	635	115	90

Чтобы устранить такой дефект, используют контрольную группу (см. гл. 5, С. 357—361). Простейший же способ снять влияние установки первого замера — производить повторный замер спустя достаточное время после первого (например, две недели) и на достаточно большой выборке испытуемых (около 50 человек). Составив таблицу замеров для всех обследуемых, мы далее анализируем, какова общая устойчивость данных и от чего зависят отклонения между двумя замерами (табл. 2, пример Г. И. Саганенко).

При повторных измерениях используют различные оценки устойчивости данных, одна из которых — это процент полных совпадений ответов на серию вопросов в двух последовательных пробах методики. Соответствующая формула:

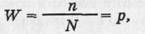
где в числителе п — количество полностью совпавших пар ответов, а в знаменателе Л7 — общая численность испытуемых, р — процент устойчивости.

По этой формуле, для примера, в табл. 2 получим:

.

полной устойчивости исходных данных. Однако ее можно повысить, заменив некоторые пункты, в частности пункт 3. по которому обнаружен наибольший разброс (всего лишь 50% совпадений). Основной критерий устойчивости информации — анализ данных по отроке. Если анализировать эти итоги по колонкам, найдем, что некоторые субъекты (В и Г особенно) дали большой разброс, а некоторые (А и Б) — почти не дали разброса. Те пункты шкалы, в которых обнаружено несовпадение даже у весьма "устойчивых" субъектов, должны быть переформулированы.

Таблица 3
Сравнение данных двух последовательных замеров в трехчленной шкале (N=28 чел.)

Ответы в I пробе о занятиях на досуге	Ответы в 11 пробе			Всего
	"Привл." (1)	"Не очень"(2)	"Не привл." (3)
"Данное занятие привлекательно" (1) "Не очень привлекательно" (2) "Занятие непривлекательно" (3)	7     4   -	3     6   3	-     1   4	10     11   7
Всего	11	12	5	28

Другим весьма полезным показателем полной устойчивости является мера сдвига, оцененная как среднеарифметическая ошибка различения градаций шкалы. Этот показатель обозначает, какую долю градации данной шкалы (в среднем) все испытуемые как бы не улавливают, т. е. каковы истинные границы различения градаций.

Например, уточним среднеарифметическую ошибку в различении трехчленной школы согласия — несогласия с каким-то суждением (пусть это будет суждение о привлекательности некоторого занятия на досуге). Приведем схему (табл. 3) и расчеты, используя данные таблицы Г. И. Саганенко.

В испытании участвуют 28 человек, из которых 17 полностью повторяют свои оценки данного занятия в обеих пробах (сумма по диагонали схемы: 7+6+4 = 17), а остальные 11 испытуемых дают разные ответы в двух пробах. Для оценки искомой ошибки вычисляем отличия ответов респондентов как сдвиги между II и I пробами, например, во II пробе из тех, кто в I пробе ответил "занятие привлекательно", 3 человека сообщили, что оно "не очень привлекательно", т. в. это разность (2—1) 3. Теперь суммируем все разности в ответах и получим меру среднеарифметической ошибки различения пунктов градации данной шкалы:

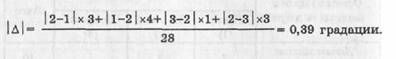
Значит, среднеарифметический "сдвиг" в оценке по трехчленной шкале составляет около 40% одного ее деления, т. е. менее половины деления, что в общем можно признать удовлетворительным, хотя и не идеальным. (Ниже, говоря о правильности измерения, мы покажем, как можно было бы уменьшить эту ошибку.)

Рассматривая устойчивость как воспроизводимость результатов измерений, можно использовать и иные показатели ее меры [200. С. 33—34], например, обычные расчеты корреляции итогов двух последовательных измерений. Показатели, рекомендуемые Г. И. Саганенко, представляются нам вполне адекватными и наглядными.

Какая же мера устойчивости удовлетворительна? Это Зависит от существа измеряемого свойства, его значимости для целей и задач исследования. В принципе для немногочленной шкалы среднеарифметическая ошибка различения градаций в 40% ее деления невысока, а соответствующая мера устойчивости (100%—40% =60%) вполне достаточна, ибо не перекрываются границы меж-ДУ двумя соседними интервалами шкалы. Если неустойчивость составила не 40%, а 60%, т. е. более половины деления шкалы, то ошибка была бы явно недопустима, ибо в среднем испытуемые не различают две соседние Градации из трех.

Для многочленных шкал, например из 10 градаций, ошибка в 60% одного деления не слишком велика, так как перекрываются два деления из 10, т. е. не 2/3, а 0,2 общей "длины" шкалы. Бели при обработке данных градации укрупнить, объединяя две соседние, то ошибка минимизируется до вполне уверенного уровня устойчивости.

Помимо показателей полной устойчивости шкалы, возможны также показатели ее относительной устойчивости. Они полезны при сравнении разных шкал, например для выбора из нескольких вариантов наиболее правильной и точной шкалы (о чем говорится ниже в этом же разделе) или для того, чтобы сопоставить уровни устойчивости измерения разных свойств, каждое из которых фиксируется шкалами разного типа и разной степени дробности.

Но прежде всего показатели следует соотносить с уровнем реальной стабильности — изменчивости изучаемого объекта, измеряемых свойств.

2) Использование нескольких лиц для измерения данного свойства. Случается, что шкала неустойчива потому, что ее пункты произвольно интерпретируются самими исследователями. В особенности это характерно для шкал качественной классификации объектов. В таких (номинальных) шкалах группы объектов классифицируют с помощью описания всех качественных признаков, по которым каждый объект относится к определенному пункту шкалы — классу.

Предположим, что выделено несколько признаков (с соответствующими индикаторами) для отнесения политической деятельности в высшую категорию по уровню активности. Чтобы выполнить эту операцию однозначно, нужно убедиться, что признаки ясно различимы и при соотнесении видов деятельности с пунктами шкалы не возникает путаницы. Скажем, такими признаками были: членство или заявленная принадлежность к какой-либо партии, движению, избирательному блоку, регулярность участия в его акциях (собраниях и публичных выступлениях, участие в голосовании на выборах и т. д.).

В этом случае объект идентифицируют одновременно несколько (минимум трое) лаборантов, использующих единую процедуру. Если данные, полученные разными лаборантами (в нашем примере они работали с текстами интервью), высоко согласуются, шкала устойчивая, если нет — неустойчивая, и мы начинаем искать другую, более приемлемую размерную величину. Причина неустойчивости шкалы — плохой отбор индикаторов.

3) Наконец, третий прием контроля эталона измерения на устойчивость — "расщепление шкалы". Шкала раздваивается на две половины. Если окажется, что измерения по каждой из них совпадают, их можно рассматривать как равноценные шкалы, суммировать данные и впредь пользоваться одновременно обеими половинами, образующими теперь единую и более надежную шкалу, чем каждая из ее составляющих.

Покажем технику "расщепления" не примере. Возьмем объектом измерения уровень удовлетворенности рабочего своей специальностью. Данные получаем путем анкетного опроса.

Проектируем две шкалы, пункты которых будут отвечать одному из пяти уровней удовлетворенности специальностью (схема 5). Каждому уровню соответствуют два суждения. Нечетные пункты образуют одну, а четные — другую половину испытываемой шкалы.

Далее производим следующие операции: (а) все 10 пунктов четной и нечетной половин перетасовываются в произвольном порядке; б) опрашиваемым предъявляют набор из 10 суждений с просьбой указать свое согласие или несогласие по каждому из них; (в) после опроса достаточной группы лиц (около 50 человек) из числа обследуемой совокупности данные группируются по двум шкалам раздельно: по нечетной половине — ( a 1), ( b 1), (с1), ( d 1), ( e 1) и по четной шкале — ( a 2), ( b 2), (с2), ( d 2), (е2).

Основная операция — (г) сопоставление итогов измерения по двум половинам испытываемой шкалы. Если корреляция между ними будет достаточно высока, эти половины можно рассматривать как части единого инструмента, измеряющего общий континуум свойств, В случае необходимости "выпадающие" суждения следует переформулировать, чтобы получить приемлемую корреляц

ию.

В таком случае итоговую шкалу образуют все 10 суждений, которые в случайном порядке предъявляются общим списком. В итоговый показатель для данного лица суммируются все баллы суждений, с которыми он выразил согласие.

Обозначив ранжированные пункты баллами от 5 (для al и аа — высшая оценка) до 1 (в, и е3 — низшая оценка), предположим, что некий субъект выразил согласие с пунктами а1+&2, отвергнув все остальные. Его суммарный балл по шкале равен 5+4=9.

Точность и правильность измерения зависят от (а) степени устойчивости измеряемого объекта или свойства, (б) чувствительности эталона измерения (дробности пунктов шкалы), (в) отсутствия система тических ошибок измерения и, конечно, (г) от устойчивости измерения.

Социальные объекты, подлежащие измерению, обладают различной степенью устойчивости. Скажем, установление состояния удовлетворенности какой-то деятельностью будет заведомо менее точным, чем регистрация частоты поведенческих актов. В первом случае сам объект измерения нестабилен. В дурном настроении человек может выражать недовольство рекламой на телевидении, а в хорошем расположении духа он будет уверять, что рекламные ролики бывают очень забавными и даже поучительными. Но вряд ли его настроение отразится на информации о том, как часто он выключает телевизор при трансляции рекламы или переключается на другую программу.

Дробность метрики — чувствительность шкалы — прямо связана с точностью измерения. Шкала в 10 делений измеряет точнее, чем в 5 или 3 деления. Но дробность пунктов шкалы нельзя увеличивать беспредельно. Надо установить оптимум, удовлетворяющий двум требованиям: максимум градаций шкалы при условии высокой устойчивости результатов измерения. Постепенно повышая дробность эталона измерения и параллельно проверяя шкалу на устойчивость, мы найдем границу, за пределами которой дальнейшее повышение дробности влечет понижение устойчивости. Это и есть оптимум чувствительности шкалы с учетом меры устойчивости измеряемого свойства. Таким образом, достижение устойчивых данных при максимальной дробности метрики повышает точность измерения. Оно будет удовлетворительно точным, если абсолютная ошибка измерения не превышает 0,5 деления шкалы. Вместе с тем, если ошибка вообще отсутствует | X j =0, то не исключено, что шкала обладает заниженной чувствительностью (особенно в случаях, когда мы предполагаем достаточную вариабельность измеряемого свойства).

Но измерение может быть вполне точным и вместе с тем... неправильным, постоянно воспроизводя какую-то систематическую ошибку, как это случается с испорченным термометром, в котором ртутный столбик изначально был фиксирован на неверной исходной отметке и постоянно завышает температуру, скажем, на 0,8 градуса.

При квантификгГции социальных характеристик проблема правильности, т. е. отсутствия уклонений от истинного значения измеряемого свойства, намного сложнее, ибо часто мы в принципе не способны установить, каковы же эти истинные значения измеряемых свойств (скажем, мнений людей по каким-то вопросам). Мы можем лишь, сопоставляя разные способы фиксирования данного свойства, добиваться устранения замеченных систематических ошибок. Каковы же эти систематические ошибки?

Одна из возможных — отсутствие "разброса" информации по шкале вследствие того, что какие-то ее пункты "не работают", т. е. не реагируют на определенное состояние измеряемого свойства. Например, при опросе все ответы концентрируются в позитивном или только в негативном полюсе шкалы. Конечно, это может быть и результатом единодушия оценок, но может быть и результатом того, что сама шкала неудачна, например, содержит какой-то пункт, сформулированный с сильным нормативным давлением на опрашиваемых. Допустим, задан вопрос об употреблении алкоголя, и крайне негативный вариант ответа гласит: "Я пью систематически и обычно до бесчувственного состояния". Сомнительно, чтобы даже заведомый алкоголик отметит такой пункт как показатель своего отношения к спиртному. Скорее всего, он выберет суждение не столь резкое, например: "Я выпиваю довольно часто". Крайне отрицательный пункт шкалы здесь "не работает*': он отпугивает. Вследствие этого шкала неправильна.

Другой причиной неправильности может быть плохая различительная способность соседних пунктов шка лы высокой дробности. Попробуйте, например, упорядочить свое отношение к 24 политикам так, чтобы уверенно указать не только приемлемого и решительно отвергаемого, но всех оставшихся из предложенного перечня расположить так же аккуратно и уверенно в порядке убывания их привлекательности. Психологически это просто невозможно, так что "срединная" часть этой так называемой ранговой шкалы будет крайне сомнительной, а вся шкала веточной и неправильной. Систематическая ошибка, скорее всего, скажется на том, что приемлемые политические деятели будут отмечаться как более привлекательные (хотя не исключено, что фактически данные лица ими не интересуются), а социально неприемлемые будут попадать в нижние уровни ранжированного ряда. 9

• 9 В данном случае для повышения надежности измерения используются операции, описываемые иа с. 103—104.

Во всех подобных случаях опытная проверка шкалы на устойчивость данных обнаружит ошибки. Но часто это показывает уже первая проба.

Правильность и точность измерения можно повысить путем расчета относительной ошибки измерения. 10

• 10 Подробнее ем. [231. С. 63—66].

Относительная ошибка позволяет сопоставлять правильность замеров по двум и более шкалам разной чувствительности и таким путем отработать оптимальный инструмент. Напомним, что, в отличие от абсолютной, относительная ошибка исчисляется не в долях погрешности деления шкалы, а в соизмеримом, определенным образом нормированном показателе.

Приведен пример расчета относительной ошибки измерения. Предположим, что в семичленной шкале оценок фиксируется намерение женщин иметь детей. В обследовании участвуют 100 молодых замужних женщин, которые дали следующие ответы на вопрос: "В какой мере Вы согласны с тем, что было бы желательно иметь ребенка?"

Полюса шкалы интерпретируются, а промежуточные пункты не имеют словесной интерпретации.

При некотором навыке и достаточном исследовательском опыте мы часто интуитивно угадываем, какова должна быть дробность метрики, обеспечивающая устойчивую информацию. Но, приступая к измерению сложных объектов, с которыми ранее не приходилось сталкиваться, социолог должен проделать ряд экспериментов, отрабатывая шкалу на точность и правильность.

Оценки 3, 2 и 1 (крайне негативное отношение к суждению) встречаются очень редко, и эту часть шкалы можно признать плохо работающей: в сумме здесь сосредоточено менее 5% всех ответов. Большинство женщин либо явно хотели иметь детей, либо не очень в этом уверены, и почти нет таких, кто отвергает идею иметь ребенка. Значит, в нашей шкале работают градации 7, 6, 5 и 4, где 4 фактически наиболее негативная установка. Диапазон работающей части шкалы: 7-4=3. Относительная ошибка данной шкалы определяется предложенной Г. И. Саганенко формулой:

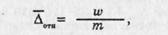
где w — оценка полной устойчивосвости шкалы, л зон реально работающей ее части.

Проверив шкалу на устойчивость, как было описано выше, мы, предположим, получили значение ц)=0,75, т.е. 75% полного совпадения ответов в двух последовательных пробах, что определенно недостаточно.

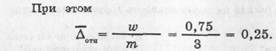
Теперь испробуем на устойчивость пятичленную и трехчленную шкалы, задавая тот же вопрос аналогичной (или той же самой) группе испытуемых в 100 человек. Допустим, что мы получим такие распределения (табл. 4),

Как видно, в пятичленной и трехчленной шкалах работают все градации, так что в негативной зоне оказывается соответственно 25% и 32% ответов (сравните с семибалльной шкалой, где в этой зоне менее 50%). Показатели полной устойчивости двух последних шкал, проверенные повторными опросами, допустим, дали соответственно 0,95 и 0,99 (в семибалльной — 0,75).

Таблица 4
Выбор более точной шкалы путем сравнения величин относительной устойчивости измерения

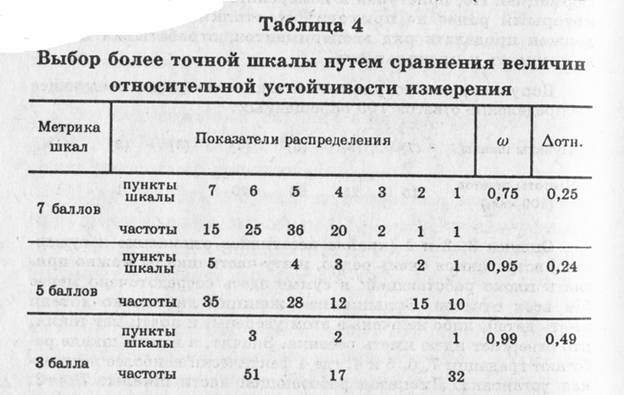
Но относительные ошибки при условии, что все градации обеих шкал работают, таковы:

для пятичленной ?отн =0,95/(5-1)=0,238 и для трехчленной ?0,99/(3-1)=0,495; округленно 0,24 и 0,49. Получаем, что относительные ошибки семичленной шкалы (0,25) и пятичленной (0,24) практически одинаковы, а трехчленной — существенно выше (0,49).

Какая из трех шкал более надежна? Вопрос решается при сравнении устойчивости шкалы и величины относительной ошибки. Устойчивость данных по пятичленной и трехчленной шкалам сопоставима: 95% и 99%. Иными словами, опрашиваемые хорошо различают градации этих шкал, лучше, чем в семичленной шкале: там устойчивость равна 75%. По этой причине последнюю надо забраковать. Остается выбор из двух оставшихся. Пятичленная шкала имеет высокую устойчивость и небольшую ошибку, а трехчленная — более высокую устойчивость и приемлемую ошибку (меньше половины градации шкалы). Но в отиошеняи к трем градациям это составит 0,49:3=0,16, а для пятичленной — 0,24:5=0,05 длины шкалы. Следовательно, пятичленная шкала втрое чувствительнее, а значит, правильнее и точнее.

Суммируем все сказанное о проверке надежности шкал в следующей схеме (схема 6).

2. Общая характеристика шкал

Применяют различные классификации измерительных эталонов. Мы будем пользоваться наиболее распространенной — континуальной классификацией (схема 7), в которой шкалы упорядочены по мере повышения их способности удовлетворять требованиям более многообразных операций с числами. 11

• 11 О типах шкал более подробно см. [112, 129]

Здесь выделено пять классов шкал, причем названия классов часто двоякие: более полные и сокращенные. Часто шкалам даются "собственные" имена по фамилии изобретателя (например, шкалы Гуттмана, Терстоуна, Гилфорда, Богардуса, Лайкерта и др.), но все они укладываются в предложенную классификацию. Далее следует запомнить, что все эти шкалы предназначены для квантификации одномерных распределений, т. е. измерения некоторой протяженности в одном и только в одном континууме свойств. Фактически же нередко пользуются многомерными измерениями, моделирующими объект (см. гл. 5, § 1).

Простая номинальная шкала

Номинальная шкала служит предпосылкой всех шкальных процедур. Она устанавливает отношения равенства между явлениями, которые включены в один класс. Пункты шкалы — эталоны качественной классификации свойств. Например, (А) рабочие ручного труда, не требующего специальной подготовки; (В) рабочие ручного труда высокой квалификации; (С) рабочие, занятые на механизированном оборудовании, средней квалификации; ( D ) рабочие механизированного труда высокой квалификации; (Е) автоматчики без навыков наладки; ( F ) пул ьтовики-наладчики.

В этой шкале, каждому из пунктов которой дается детальная эмпирическая интерпретация (по индикаторам конечного перечня соответствующих профессий), интуитивно угадывается некоторый порядок: группы рабочих перечислены по мере повышения механизации труда и, возможно, по мере роста квалификации. Однако интуиция — не доказательство. Шкала остается неупорядоченной.

Более явный пример — группировка по мотивам увольнения с работы: (а) не устраивал заработок; ( b ) неудобная сменность; (с) плохие гигиенические условия труда; ( d ) неинтересная работа и т. д. Упорядочить эти пункты невозможно: они не располагаются в континуум. Символическая запись номинальной неупорядоченной шкалы такова:

(А) ^ (В) ^ (С) ^... ^ (К), где знак ^ означает дизъюнкцию (либо—либо).

Операции с числами для номинальной шкалы следующие.

1. Нахождение частот распределения по пунктам шкалы с помощью процентирования или в натуральных единицах. Нетрудно подсчитать численность каждой группы и отношение этой численности к общему ряду распределения (частоты).
2. Поиск средней тенденции по модальной частоте. Модальный (Мо) называют группу с наибольшей численностью.
   Эти две операции (1) и (2) уже дают представление о распределении социальных характеристик в количественных показателях. Его наглядность повышается отображением в диаграммах (рис. 6, где А — модальная группа). Во всех трех случаях за 100% принята общая численность обследованных. Диаграмма 6, а позволяет, однако, отразить распределения, в которых сумма процентов превышает 100, т. е. некоторые обследуемые могут попасть в несколько секций шкалы одновременно (например, совмещают различные виды деятельности).
3. Самым сильным способом количественного анализа является в данном случае установление взаимосвязи между рядами свойств, расположенных неупорядоченно. С этой целью составляют перекрестные таблицы (схема 8).

Помимо простой процентовки, в таблицах перекрестной классификации можно подсчитать критерий сопряженности признаков по Пирсону: хи-квадрат (х 2 ) — простейший показатель обоснованности вывода о наличии или отсутствии связи между сопоставляемыми характеристиками, т. е. связанности качественных классификаций. Коэффициент Чупрова (Т-коэффициент) позволит по той же таблице определить напряженность связи, если хи-квадрат показывает, что она имеет место. 12

• 12 Об использовании различных коэффициентов при работе с неупорядоченными номинальными шкалами см. [218, С. 189—172, 189—199]. Интересен метод, предложенный С. В. Чесноковым, который позволяет анализировать данные, фиксированные в номинальных шкалах, используя относительно "естественный" язык представления результатов, хорошо доступных неспециалистам [285].

Частично упорядоченная шкала

Эта шкала служит для установления отношений равенства между явлениями в каждом классе и отношений последовательности в терминах ">" или "<" между несколькими* но не всеми классами (минимум двумя из п классов, где п>2). Она обычно используется как промежуточный этап при разработке полностью упорядоченных шкал. Иногда, однако, ранжировать весь ряд не удается.

Рис. 6. Виды диаграмм распределения качественных признаков в номинальной неупорядоченной шкале: а — столбиковая диаграмма; 6 — ленточная диаграмма; в — секторная диаграмма; А, В, С, D и т. д.— отдельные качественные признаки, например, профессионально-квалификационные группы работников, отношение к политическим партиям и т. д.

Так, из приведенного выше примера с группами по функциональному содержанию труда возьмем позиции (А), ( D ), (Е) и ( F ). Можно утверждать, что измеренные по двум параметрам (механизация и квалификация) позиция (А) ниже позиции ( F ),так как в первом случае оба параметра имеют низкий уровень» во втором — высокий. Позиция (К) явно выше, чем (А), и ниже, чем ( F ). Позиция (Е) — в одинаковом отношении к (А) и ( F ). Но отношение между ( D ) и (Е) установить трудно, так как для этого надо приравнять ранг по механизации рангу по квалификации, что невозможно сделать без специальных исследований. Значит, позиции ( D ) и (Е) несопоставимы в понятиях "больше"—"меньше".

Такая зависимость описывается фигурой

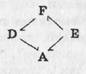
Здесь соединительные линии обозначают сопоставимость рангов и указывают их соотношения (>и<), отсутствие связи (. D ) ...( E ) указывает на то, что позиции несопоставимы.

Операции с числами для данной шкалы следующие.

1. Все операции, перечисленные для неупорядоченной номинальной шкалы.
2. С каждым из полностью упорядоченных отрезков ряда можно обращаться как с полностью упорядоченной шкалой наименований. Полученные по отрезкам данные сравнивают в однозначных показателях по модальным группам или коэффициентам корреляции рангов.

Провалы в частично упорядоченной шкале объясняются тем, что признак континуальной классификации не выдержан строго или использовано два континуума, отношение между которыми плохо изучено. В нашем примере с группами по содержанию труда можно перевести шкалу в полностью упорядоченную, если прибавить к двум имеющимся третий, "сквозной" критерий. Но практически данный вид шкалы используется крайне редко.

Порядковая шкала

Полностью упорядоченная шкала наименований устанавливает отношения равенства между явлениями в каждом классе и отношения последовательности в понятиях ">" и "<" между всеми без исключения классами.

Упорядоченные номинальные шкалы общеупотреби-мы при опросах общественного мнения. С их помощью измеряют интенсивность оценок каких-то свойств, суждений, событий, степени согласия или несогласия с предложенными утверждениями.

Вот обычные наименования пунктов таких шкал: "вполне согласен", "пожалуй, согласен", "затрудняюсь ответить", "пожалуй, не согласен", "совершенно не согласен"; или: "уверен, что так", "думаю, что так", "затрудняюсь сказать", "думаю, что не так", "уверен, что не так"; или: "целиком одобряю", "одобряю в основном", "затрудняюсь сказать", "в основном не одобряю", "совершенно не одобряю"; или: "так всегда бывает", "так бывает иногда", "бывает и так, и иначе", "так обычно не бывает", "так никогда не бывает"; или: "вполне удовлетворен", "удовлетворен", "скорее удовлетворен, чем не удовлетворен", "затрудняюсь сказать", "скорее не удовлетворен, чем удовлетворен**, "не удовлетворен", "совершенно не удовлетворен"; или: "это очень важно", "это важно", "трудно сказать, важно это или нет", "это неважно", "это не имеет никакого значения" и т. п.

Упорядоченные номинальные шкалы имеют и более сложные конструкции (например, шкала Гуттмана, которую мы рассмотрим ниже), а в простейшем варианте являются составными элементами многих мерительных операций, в особенности методов суммирования оценок по ряду шкал (см. операции с числами, пункт 2).

Весьма часто употребляемая разновидность шкал этого типа — ранговые. Они предполагают полное упорядочение каких-то объектов от наиболее к наименее важному, значимому, предпочитаемому. Например, можно ранжировать соотносительную важность тех или иных методов решения общественной проблемы, предпочтения тех или иных действий ради достижения желаемой цели, какие-то ценностные суждения и т. д. Задание на ранжирование респонденту (или эксперту) обычно формулируется так: "Из перчисленных ниже суждений (возможных решений некоторой проблемы...) выберите самое для Вас предпочтительное, затем — наименее предпочтительное, а остальные расположите от первого к последнему".

Далее предлагаются объекты для ранжирования и указывается место, где следует приписать нужный ранговый порядок:

Указание в скобках слева значения рангов — результат работы опрашиваемого. В опросном листе обозначено лишь место (оставлена линейка) для приписывания ранга каждому объекту. Важно иметь в виду, что при обработке данных шкала в цифровом выражении может быть "перевернута" в обратном порядке, т. е. последнему, низшему рангу можно приписать наименьшее числовое значение — 1, а первому — наибольшее. Тогда последовательность 1, 2,... и т. д. будет соответствовать возрастанию значимости объектов.

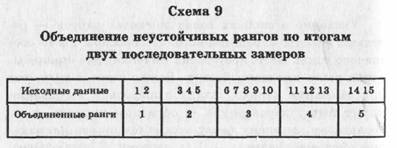
Полезно не забывать о том, что численность объектов для ранжирования не может быть слишком большой, скажем — 15. В противном случае данные ранжирования крайне неустойчивы. Кроме того, в любом варианте более устойчивы первые и последние ранги (при повторных опросах опытных групп они обычно приписываются тем же объектам), а срединная зона, как правило, менее устойчива. Поэтому для повышения надежности данных ранжирования следует после проведения пробы на повторный опрос небольшой группы испытуемых (микромодель будущей выборочной совокупности) объединить в один ранг те из них, которые обнаружат наибольшую неустойчивость.

Предположим, что после второго замера произошли сдвиги рангов: 1—2, 3—5, 6—10, 11—13 и 14—15. Иными словами, многие из тех, кто, например, первоначально приписывал данному объекту 6-й ранг, во втором замере приписали ему 7-й, 8-й, 9-й или даже 10-й. Определив неустойчивые области, мы можем в основном исследовании, не изменяя инструкции для ранжирования, при анализе данных преобразовать 15-ранговую шкалу в 5-ранговую, как показано на схеме, т. е. обеспечить большую устойчивость и надежность данных ранжирования (схема 9). 13

• 13 Подробнее см. [232. C. 74-77 ]

Помимо того, что оценка уровня устойчивости итогов ранжирования — способ повышения надежности шкалы, это к тому же и показатель содержательного характера. Объекты, в отношении которых опрашиваемые неуверены (ранги таких объектов смещаются), по-видимому, обладают для них меньшей субъективной значимостью, выпадают из сферы повседневных интересов.

Нередко приходится ранжировать множество объектов, существенно больше 15. Объединение рангов здесь также помогает повысить устойчивость, но одновременно резко снижает чувствительность шкалы. В таком случае можно прибегнуть к несколько более трудоемкой для анализа, но более простой для респондента и более надежной процедуре ранжирования методом парных сравнений [75; 193; 231; 265].

Ранжирование состоит в том, что предлагается попарно сопоставить предпочтительность объектов (пусть очень обширного списка) путем всех возможных их парных комбинаций.

Допустим, что у нас имеется 25 кандидатов, участвующих в выборах, ранжировать которых задача психологически почти невыполнимая. Тогда при массовом опросе накануне выборов (во время самих выборов избиратель просто голосует "да—нет" в отношении каждого кандидата) предложим следующее задание: "Из всех перечисленных попарно кандидатов в каждой из пар выберите того, который кажется Вам более предпочтительным из данной пары. Не пропускайте ни одной строчки. Предпочитаемого кандидата обведите в кружок" (схема 10).

Поскольку объекты А и Е имеют равное число выборов (по 1), им приписывается одинаковый ранг, а так как число перестановок оказывается весьма большим, то одинаковые значения получат несколько объектов. Доказано, что результаты такого ранжирования весьма устойчивы. 14 И тогда в нашем примере основания для прогноза исхода реальных выборов становятся более надежными (хотя они будут зависеть и от других, неучтенных здесь обстоятельств). 15

• 14 Надежность парных сравнений существенно повышается, если предлагается оценить предпочтительность одного из двух объектов не дихотомически (либо-либо), а в пяти-семибалльной шкале. Такой способ применил В. А. Лосепков при разработке методики изучения социальных установок [235. С. 220— 222].
• 15 См. об этом на с. 470.

Операции с числами. Прежде всего следует помнить, что интервалы в школе не равны, поэтому числа обозначают лишь порядок следования признаков. И операции с числами — это операции с рангами, но не с количественным выражением свойств в каждом пункте.

• 1. Числа поддаются монотонным преобразованиям: их можно заменить другими с сохранением прежнего порядка (именно поэтому шкалы данного типа называют также порядковыми). Так, вместо ранжирования от 1 до 5 можно упорядочить тот же ряд в числах от 2 до 10 или от (—1) до (+1). Отношения между рангами останутся неизменными:

Это свойство важно в тех случаях, когда данные, измеренные шкалами с различным числом интервалов, приходится приводить к "общему знаменателю", т. е. выражать в одной шкале с постоянной величиной заданных интервалов.

• 2. Суммарные оценки по ряду упорядоченных номинальных шкал — хороший способ измерять одно и то же свойство по набору различных индикаторов. Такое суммирование, предложенное Лайкертом, получило название "кафетерий" ("кафетерий" — это как бы набор блюд в меню с подсчетом общей стоимости обеда).

Рассмотрим пример суммирования оценок по шкале, измеряющей отношение женщин к детям [353. С. 134—137]. Опрашиваемых просят указать вариант ответа на каждое суждение, расположенное по вертикали (схема 11).

Прежде чем суммировать итоговый балл, следует оценить порядок всех пунктов десяти шкал, составляющих "кафетерий". Очевидно, что пункты 1, 2, 5, 9 и 10 выражают положительное отношение к детям, а пункты 3, 4, 6, 7, 8— отрицательное. Важно, чтобы число позитивных и негативных суждений было одинаковым, или, как в данном случае, различалось не более, чем на 1/10.Тогда для первого ряда ответов "совершенно согласна" оценивается баллом "5" и "совершенно не согласна" — баллом "1**, а для второго ряда — в обратном порядке.

Общая оценка для нашего примера складывается из баллов по строкам:

• 3. Для работы с материалом, собранным по упорядоченной шкале, можно использовать, помимо модальных показателей, поиск средней тенденции с помощью медианы ( Me ), которая делит ранжированный ряд пополам. Медиана применяется для обнаружения порогов на шкале: справа и слева от нее располагаются признаки, тяготеющие к противоположным полюсам (см. также пример в табл. 17).
• 4. Наиболее сильный показатель для таких шкал — корреляция рангов (по Спирмену — р или по Кендал-лу — R ). Ранговые корреляции указывают на наличие или отсутствие функциональных связей в двух рядах признаков, измеренных упорядоченными номинальными шкалами.

Метрическая шкала равных интервалов

Класс метрических шкал, в отличие от номинальных, устанавливает отношение между пунктами не просто в понятиях больше-меньше, но позволяет фиксировать величину интервала. Заметим, однако, что использование метрических шкал в социологическом исследовании случается далеко не так часто, как порядковых.

Шкала интервалов представляет собой полностью упорядоченный ряд с измеренными интервалами между пунктами, причем отсчет начинается с произвольно избранной величины.

Главная трудность в построении таких шкал — обоснование равенства или разности дистанций между пунктами. Процедуры такого доказательства мы рассмотрим в следующем разделе на примере шкалы Тёр-стоуна.

Неопытные исследователи принимают иногда за интервальную шкалу шкалы балльных оценок. Но это псевдометрическая шкала. Так, один из вариантов псевдошкалы с равными интервалами — "термометр общественного мнения". Это шкала в 100 делений, где крайние точки (100 и 0) словесно интерпретируются. Например, "если вы категорически согласны с приведенным суждением, укажите свое положение на термометре как 100°", "если вы категорически не согласны, укажите 0°. В действительности, нет оснований полагать, что лица, отметившие по термометру 35° и 42°, столь же различаются в своих оценках, как отметившие 45° и 52°. Интервал в Т (42°— 35° = 7 ° ( 52°— 45° = 7°) — чисто условный, так как одни люди обладают высокой способностью дифференцировать свои оценки, а другие вовсе не могут различать нюансы. Так что данная шкала меряет не что иное, как те же ранги, что и упорядоченная номинальная, каковой она фактически и является.

В отличие от "термометра" общественного мнения шкалы Тёрстоуна имеют веские основания равенства интервалов, в чем мы дальше сможем убедиться.

Операции с числами в интервальной метрической шкале богаче, чем в номинальных шкалах.

1. Числа в таких шкалах остаются неизменными после линейных преобразований: у=ах+ b . Начало (точка отсчета) на шкале избирается произвольно ( b ); также произвольно избирается размерная величина (а). Например, максимальный балл по шкале у=21, если размерная величина а=2, число интервалов x =10 и отсчет начинается с b =1, т. е. ах+ b =у, или 2x10+1=21. Ранги переменных на этой шкале равны в отношении "х" и "у". Это значит, что можно свободно менять точку отсчета и числовое значение размерной величины. Например, от шкалы в 100 делений можем легко перейти к шкале с любым другим числом делений, притом отсчет можно начать с любой точки натурального ряда чисел. Так обычно переходят от измерения температуры по Цельсию к термометру по Реомюру или Фаренгейту — ранги температур остаются прежними.
2. Появляются новые возможности корреляционного и регрессионного анализа. Вместо рангового коэффициента можно использовать более чувствительный коэффициент парной корреляции по Пирсону (г) и коэффициенты множественной корреляции. Последние хороши тем, что позволяют соотнести (оценить) изменения в одной переменной с изменениями в другой или в целом ряде других переменных.

Шкала пропорциональных оценок

Здесь мы имеем дело с идеальной или абсолютной метрической шкалой, напоминающей шкалу равных интервалов, но с одним преимуществом: отсчет в этой шкале начинается не с произвольной точки, а с экспериментально установленного нулевого пункта. Для таких шкал применимы решительно все операции с числами, так как можно определить, на сколько или во сколько данный пункт на шкале превышает другой. Подобные шкалы приняты в точных науках, где нулевой пункт (точка отсчета — из чего и происходит название "точные науки") экспериментально зафиксирован.

Идеальные метрические шкалы успешно применяются для измерения некоторых физиологических и психических свойств человека. Точка отсчета определяется в этих случаях как порог восприятия и порог насыщения. Известно, например, что существует среднестатистический порог восприятия звуковых колебаний. То же относится и к некоторым психическим реакциям людей (например, порог различения сходных фигур).

В социологии шкалы такого рода имеют весьма ограниченное применение. Ими пользуются для измерения протяженностей во времени и пространстве, для отсчета натуральных единиц (денежных единиц, продуктов деятельности» поступков). Во всех этих случаях нулевой пункт четко фиксируется.

Что касается измерения качественных свойств социальных явлений, поиск нулевого пункта как точки отсчета заведомо обречен на неудачу. Как правило, социальные процессы и характеристики варьируют от ситуации к ситуации столь сильно, что нулевой пункт может быть установлен только как среднестатистическая величина в большой массе событий.

Операции с числами, как уже говорилось, для идеальных шкал не имеют никаких ограничений. Можно использовать все доступные математике операции с натуральными числами.

Теперь, ознакомившись с различными типами шкал, мы могли бы заметить, что собственно измерение начинается как будто бы с введения обоснованной метрики в шкалах равных интервалов (типа шкал Гуттмана) и в шкалах пропорциональных оценок. Номинальные упорядоченные шкалы предполагают ранжирование объектов (свойств), а простые номинальные шкалы есть лишь их классификация.

Однако классификация в номинальной шкале, а тем более ранжирование объектов — это тоже измерение, так как с помощью данных процедур мы фиксируем меру, протяженность, континуум. В социологии, а также в психологии приходится, как правило, довольствоваться такими элементарными способами первичного измерения. Но этого, в общем, достаточно для того, чтобы фиксировать тенденцию изучаемого социального процесса. На большее социолог не претендует, да вряд ли и должен претендовать.

3. Поиск однонаправленного континуума в шкалах Гуттмана (упорядоченная номинальная шкала)

Поиск одномерного континуума свойств некоторой неявной (латентной) характеристики по внешним ее проявлениям — довольно сложная задача. Один из вариантов ее решения предложил Луи Гуттман [64]. Шкала Гуттмана предназначена для измерения установок, т. е. субъективного отношения к объекту, и обладает двумя важными достоинствами: кумулятивностью и репродуктивностью.

Такие арифметические действия, как сложение, умножение и возведение в степень, ранжированы по кумулятивной, т. е. накопительной, шкале. Тот, кто умеет возводить в степень, непременно умеет умножать и складывать. Но кто умеет складывать, вовсе не обязательно умеет умножать (не говоря о возведении в степень). С принципом кумулятив-ности связана и реп род уктивн ость. Зная максимальные математические возможности некоего человека, можно надежно предсказать его возможности в менее ответственном испытании, причем все это относится к одному и только одному параметру. В нашем случае — это накопительные операции с натуральными числами (а не что-то иное).

Рассмотрим вымышленный пример построения шкало-граммы для измерения социальных установок людей по поводу перехода на новую систему организации труда. Предлагая опрашиваемым серию суждений, мы просим высказать свое отношение к каждому из них. При этом несогласие с суждением, в котором критикуется новая система, наряду с согласием по поводу благоприятствующих ей мнений оценивается как положительное отношение и дает респонденту 1 балл в суммарном показателе.

В следующем списке согласие с суждениями 1, 2, 5, 6 и несогласие с суждениями, 3, 4, 7, 8 свидетельствуют о благоприятном отношении к новой системе организации (обратите внимание: численность позитивных и негативных Утверждений должна быть равной).

Список исходных суждений для построения шкалограммы

1. Новая система организации, несомненно, способствует повышению производительности труда. ----Согласен (1)----Не согласен (0)
2. В целом эта система лучше той, что применялась прежде. ----Согласен (1)----Не согласен (0)
3. Некоторые стороны новой системы организации плохо продуманы.
   ----Согласен (0)----Не согласен (1)
4. Как и любая другая система организации, новая система имеет немало минусов.
   ----Согласен (0)----Не согласен (1)
5. Новая система удачно сочетает материальное и моральное стимулирование работников.
   ----Согласен (1)----Не согласен (0)
6. Доводы в пользу новой системы очень убедительны. ----Согласен (1)----Не согласен (0)
7. В прежней системе было немало хорошего, что утрачено п новой организации.
   ----Согласен (0)----Не согласен (1)
8. Преимущества новой системы организации совершенно не ясны.
   ----Согласен (0)----Не согласен (1)

Если приписать каждому положительному ответу 1 балл и каждому отрицательному — нулевой, то человек, максимально благоприятно оценивающий новую систему организации, получит 8 баллов, а противник этой системы — 0 баллов. Остальные распределяются в промежутках между двумя полюсами шкалограммы.

Процедура отработки шкалограммы состоит в следующем [353. С. 143—157].

• (1) Отбирается экспериментальная группа, которой предлагают высказаться по поводу суждений, предположительно образующих континуум. В составе группы должны быть представители обследуемой категории населения. Численность группы — около 50 человек (в нашем примере для простоты возьмем 15 человек).
• (2) Высший балл по шкале определяется суммированием оценок по каждому ответу. В нашем примере для каждого суждения возможны оценки 1 или 0. В более сложных шкалах предлагается высказать полное или частичное согласие (несогласие) с каждым суждением:

4. Совершенно согласен.

3. Согласен.

2, Не знаю, не могу ответить.

1. Не согласен.

0. Категорически не согласен.

В этом случае высшая оценка в шкалограмме из 8 суждений составит 8x4=32, а низшая, как и прежде, = 0.

• (3) Данные опроса экспериментальной группы располагаются в матрицу так, чтобы упорядочить опрошенных по числу набранных баллов от высшего к низшему (схема 12).

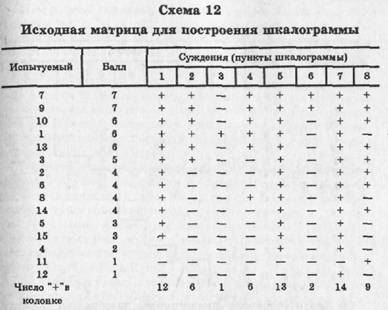
Знак "+" означает благожелательное отношение к объекту оценивания, "—** означает неблагожелательное отношение.

Анализируя полученную шкалограмму, видим, что она весьма близка к идеальному варианту. Например, балл 3 для суждения № 5 определенно связан с положительным отношением к новой системе по суждениям 1, 5 и 7; балл 6 по суждению № 10 означает благоприятное отношение по пунктам 1, 2, 4, 5, 7 и 8. Не очень удачны пункты 3 и 7. С суждением №3 ("Некоторые стороны новой системы организации плохо продуманы") почти никто не согласен, что дает каждому по дополнительному баллу. Зато с пунктом 7 ("В прежней системе было немало хорошего, что утрачено в новой организации") подавляющее большинство согласно, и это отнимает у них по баллу. Оба пункта, следовательно, плохо дифференцируют опрошенных. Наиболее удачны суждения №2 и 4, которые делят респондентов на сторонников и противников новой системы организации.

• (4) Для очевидности шкалограммы преобразуем таблицу так, чтобы получить идеальную "лесенку" (схема 13).

Идеальная шкалограмма предполагает, что ответ на один из вопросов должен повлечь за собой определенный ответ на следующий за ним по нисходящей ветви. Значит, первая задача состоит в том, чтобы выяснить, действительно ли ответы на эти вопросы образуют одномерный континуум.

Число лиц в экспериментальной группе достигает 50-100 человек, а число пунктов также достаточно велико. Кроме того, на каждый вопрос можно было бы дать пять ответов (от "совершенно согласен" до "совершенно не согласен"). Поэтому вращение рядов шкалограммы — утомительная операция. Гуттман, не имея компьютера, разработал несколько технических приемов. Один из них: деревянная доска, на которой передвигаются цветные фишки, соответствующие позитивным— негативным ответам. Конечно, при современных возможностях использовать компьютер все эти сложные перестановки максимально упрощаются (в SPSS для этого есть специальная программа).

После упорядочения респондентов, как показано в схеме 12, упорядочиваются пункты от максимума к минимуму благожелательных ответов. Внутри пункта производится сортировка субъектов так, чтобы набравшие максимум баллов располагались выше тех, кто набрал следующее за ними число баллов.

При ручной сортировке в карточку респондента заносятся ответы "за" и "против" каждого пункта информации, а также, общее число набранных баллов. Первая сортировка производится по колонке № 1 на всю выборку, затем — по остальным колонкам, т. е. вопросам.

Так определяется порядок вопросов в матрице от набравшего максимум до набравшего минимум благожелательных ответов. Вторая сортировка — внутри данной колонки ранжируются субъекты, набравшие максимум—минимум баллов. Составляется матрица, которую анализируем с точки зрения наличия континуума в ответах.

Вернемся к нашей шкалограмме. На схеме 13 видно, что имеется 6 случаев отклонения от идеального распределения: три благоприятных суждения выпали в "запретную" зону справа и три неблагоприятных суждения выпали в "запретную" зону слева. Используем пример с умением считать: перед нами тот случай, когда умеющий умножать почему-то не умеет складывать, а не умеющий умножать умеет возводить в степень. Иными словами, это — парадокс.

• (5) Идеальную шкалограмму мы не получили. Но это вообще маловероятно. Следует стремиться к некоторому оптимальному варианту. Такой вариант задается числом допустимых отклонений в ответах экспериментальной группы. Подсчет допустимого числа отклонений производится путем исчисления коэффициента репродуктивности шкалограммы:

R = 1 – n \ KN

где R — коэффициент репродуктивности, К — число пунктов (в нашем случае = 8), по которым следует дать ответ, N — число испытуемых (в нашем случае =15), n — число ошибочных ответов, которые располагаются справа или слева от идеальной вертикали.

Коэффициент желательной репродуктивности задается исследователем как надежный интервал допустимой ошибки. Желательно получить не более 10% ошибочных ответов. Тогда коэффициент репродуктивности должен выражаться числом 0,90. Число допустимых ошибок подсчитываем, преобразуя формулу:

п = (1 - R )( KN ).

В нашем примере для R =0,90 при 8 суждениях и 15 испытуемых число допустимых ошибок составит (1 — — 0,90)х(8х15)=12, т.е. существенно меньше, чем оказалось в реальности. Фактический коэффициент репродуктивности нашей шкалы достаточно высок и равен 0,95.

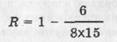
Можно повысить этот коэффициент до 0,98, если убрать суждение № 8, по которому имеются три ответа, отклоняющиеся от идеального континуума. Тогда:

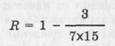
В случае, если на каждое суждение предполагается ответ по шкале в пять пунктов (4 = "совершенно согласен" ... О = "совершенно не согласен"), коэффициент репродуктивности может быть улучшен и за счет выбрасывания суждений, дающих много отклоняющихся ответов, и за счет укрупнения дробной шкалы согласия—несогласия с суждением.

• (6) Шкала с коэффициентом репродуктивности не менее 0,90 готова. В массовом обследовании все пункты шкалы тасуются случайным образом. Ранг каждого опрашиваемого определяется по сумме набранных баллов.

Данные, полученные на группу, можно усреднить, подсчитав среднеарифметический ранг для этой категории лиц и сравнивая его с аналогичным средним показателем для другой категории. В нашем примере было бы интересно знать расхождение в оценках нововведений на государственных и частных предприятиях, руководителей и рядовых сотрудников.

4. Использование судей для отбора пунктов в шкалу равных интервалов Терстоуна

Выше мы рассмотрели процедуру фиксирования одномерного континуума. Но часто возникает прямо противоположная задача: нужно измерить субъективные отношения людей к весьма сложным явлениям, причем мы либо не можем, либо не желаем расчленять это отношение по составляющим его аспектам. Как и в построении шкалограмм, речь вновь идет о поиске латентной (скрытой) характеристики по ее внешним проявлениям, но цели поиска — иные.

Луи Тёрстоун [372] исходил из верной предпосылки, что психологическая установка человека на социальные объекты содержит эмоциональное отношение. Поэтому задача измерения сводится к тому, чтобы найти степень позитивной или негативной напряженности такого отношения. Процедура конструирования шкалы равных интервалов разрабатывалась Тёрстоуном по аналогии с процедурами поиска психофизиологических порогов восприятия.

Представим, что перед нами множество предметов одинакового внешнего вида, но незначительно отличающихся по весу. Перебирая предметы и взвешивая их поочередно на руке, определим минимальную величину, которая ощущается как разница двух близких весов. Это и есть интервал порога восприятия тяжести. Аналогичным образом строится процедура поиска субъективного порога различения оценочных суждений в шкале Тёрстоуна.

Разработка шкалы производится в несколько этапов.

• (1) Вначале придумывается множество суждений позитивного и негативного характера, каждое из которых выражает отношение к некоторому объекту, явлению, социальной проблеме и т. п. в зависимости от поставленной задачи. Например, это могут быть суждения, выражающие отношение к соблюдению законности: "Законы следует соблюдать во всех случаях"; "Бывают обстоятельства, когда нарушение определенного законодательного положения допустимо"; "Если бы наказания за несоблюдение законов были более строгими, нарушений бы не было"; "Я не очень беспокоюсь о нарушении закона, если никто об этом не сможет узнать" и т. д.
• Суждения должны быть вполне однозначны и понятны, а главное, сформулированы так, чтобы с ними не смогли согласиться люди, придерживающиеся прямо противоположных взглядов. Начальная численность таких суждений ориентировочно около 30. Для их формулировки можно привлечь представителей потенциальной аудитории опроса.
• (2) Суждения, записанные на отдельные карточки, предлагаются "арбитрам", в качестве каковых выступают случайным образом отобранные представители опрашиваемой аудитории. Численность судей — около 50 человек.
• (3) Этим арбитрам предлагается рассортировать все суждения одно за другим, последовательно в 11 групп, обозначенных буквами от А до Л. Возле картонки с буквой "А" надо поместить суждения, в которых, по мнению арбитра, выражено максимально положительное отношение к данному объекту или явлению, а возле картонки с буквой "Л" — максимально негативное. Возле картонки с буквой "Е" должны помещаться суждения нейтрального, по мнению арбитра, характера, а остальные — в зависимости от их содержания в промежутках от "А" до "Е" и от "Е" до "Л". Судей предупреждают, что не надо стараться распределить суждения по всем группам поровну, но только в зависимости от их смысла.
• (4) После окончания сортировки начинается тщательный анализ, с тем чтобы установить: (а) степень согласованности судейских решений и (б) "цену" каждого суждения на шкале в 11 интервалов (эта шкала найдена оптимальной).

Таблица 5
Анализ распределения судейских оценок для построения шкалы равных интервалов

Пункт шкалы	Число суден, поместивших суждение в этот пункт	Процентная доля ко всему числу судей	Суммарный (кумулятивный) процент
0	0	-	-
1	0	-	-
2	0	-	-
3	0	-	-
4	0	-	-
5	0	-	-
6	12	4	4
7	12	4	8
8	60	20	23
9	66	22	50
10	90	30	80
11	60	20	100
Итого	300	100

Анализ распределения судейских оценок производится путем исчисления медианы и отклонений от медианной точки.

Подсчитаем судейские оценки для одного из суждений по табл. 5. Имея такое распределение, построим график, где по вертикали отложим кумулятивный процент, а по горизонтали — шкалу из 11 интервалов. Кривая пересекает вертикали в точках, соответствующих медианной оценке для двух соседних пунктов на шкале. Поэтому они оцениваются дробями: 3,5 или 6,5, но не 3 или 6 (рис. 7).

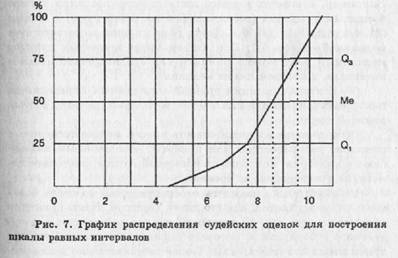
В районе 0 — позитивный полюс, 5 — нейтральный, 11 — негативный. Медианная оценка определяется по среднему перпендикуляру на базовую шкалу из 11 пунктов. Перпендикуляр опущен из точки, разделяющей ранжированный ряд судейских решений ровно пополам. Цена суждения по медиане в нашем случае: S = 8,5.

Определим, насколько единогласны судьи в своих решениях об этом суждении по квартальному отклонению ( Q ):

Q = Va ( Q 3 - Q ,);

или для нашего примера

Q = V 2(9,3 - 7,3)=1,0.

• (5) В итоговую шкалу отбираются суждения, получившие наиболее согласованные оценки. Например, если имеются три суждения со сходной ценой (скажем, от 8,1 до 9,2) и с квар тальными отклонениями, равными 1,0; 1,3; 1,5, то в итоговую шкалу отбирается суждение с Q = l ,0, как получившее наиболее согласованную оценку судей.

В окончательном виде шкала обычно содержит от 15 до 30 суждений, каждое из которых имеет "цену" или "вес", определенный по медиане судейских решений.

Очевидно, что, коль скоро арбитраж 50 судей позволил найти пороги различения между суждениями, шкалу можно признать метрической шкалой равных интервалов с отсчетом от О.

• (6) Для использования в массовом опросе все суждения тасуются как игральные карты. Опрашиваемые выражают согласие или несогласие с каждым из предложенных суждений. Цена суждения в опросном листе не проставлена: веса всех суждений записаны в инструкции по обработке данных.
• (7) Индивидуальный ранг опрошенного по шкале Тёрсто-уна определяется как медиана весов принятых им суждений. Например, в ответах некоего лица содержится всего четыре принятых суждения (все остальные им отвергнуты) с весами ( S ): 4,4; 4,8; 5,1; 5,6; 6,1. Тогда ранг индивида соответствует медианной оценке 5,1. При четном числе принятых пунктов медианный ранг можно принять как среднеарифметическое интервала, в котором лежит медиана.
• (8) Ранговая позиция группы опрошенных определяется как среднеарифметическая рангов всей совокупности, составляющей группу.

Обоснованность и устойчивость шкалы можно проверить с помощью уже известных нам приемов: использование независимого критерия, контроль по известной группе, повторное измерение с интервалом во времени.

Не обязательно начинать отбор суждений со столь большого числа вариантов, как это делал Тёрстоун. Наша практика показывает, что 30—50 суждений вполне достаточны для судейского отбора, после которого определится десяток вполне приемлемых пунктов шкалы. Также не обязательно вовлекать в работу очень большое число судей: можно получить статистически устойчивые данные на 50—60 экспертах.

Снижение точности замера за счет снижения дробности шкалы существенно повышает ее надежность. Если предлагать судьям расположить суждения не в 11, а в 5 интервалов, итоговая шкала будет более надежна, но менее точна. Выбор в пользу большей—меньшей точности зависит от предмета исследования и значимости гипотез, а также от того, насколько точно измеряются в нем другие переменные. Если большинство переменных измеряется по трехчленным и пятичленным шкалам, но только одна — по 11-членной шкале, и притом все переменные подлежат взаимной корреляции, в этом случае повышенная точность 11-членной шкалы — излишняя роскошь. Она не оправдывается логикой сопоставления с другими переменными.

Работа с экспертами, аналогичная описанной выше, широко применяется и в других случаях, когда мы обращаемся к выборочной группе из массива обследуемых для того, чтобы глазами будущих испытуемых проверить соотносительную значимость оценок, придаваемых пунктам шкалы [232. С. 109—128].

5. Четыре важнейших ограничения квалификации первичных социальных характеристик

Мы рассмотрели различные приемы перевода качественных социальных признаков в их количественные выражения. Это очень ответственный момент процедуры социологических исследований.

Применение количественных методов и использование статистических показателей взаимосвязи социальных явлений и процессов как бы возводит социологию в ранг подлинной "строгой" науки. Создается впечатление математической точности выводов. Между тем квантификация сложных и далеко не однозначных социальных реалий накладывает немало ограничений на собственно математические операции с их измерениями. Математик работает с простыми однозначными абстракциями, в основе которых суждение "есть— нет" (т. е. наличие—отсутствие данного свойства). Социолог обязан постоянно помнить, что в действительности скрывается за величинами и символами, которыми мы оперируем.

В данном случае, мы обращаем внимание только на некоторые ограничения, связанные со специфическим видом формализации социальных данных, имея в виду наиболее распространенные и сравнительно простые приемы использования математической статистики в социологии.

Первое ограничение — соразмерность количественных показателей, фиксированных разными шкалами в рамках одного исследования.

Суммируем сведения о возможностях операций с числами в описанных выше шкалах (схема 14) 16

• 16 Здесь частично используется схема из работы С. С. Паповяпа [201. С. 60].

Более сильная шкала отличается от ближайшей к ней относительно слабой тем, что допускает более широкий диапазон математических операций с числами. Все, что допустимо для слабой шкалы, допустимо и для сильной. Но не все, разрешимое для сильной, позволительно для слабой шкалы. Поэтому смешение в анализе мерительных эталонов разного типа приводит к тому, что не используются возможности сильных шкал: в этом случае все операции с числами должны удовлетворять требованиям, предъявляемым к относительно слабым шкалам.

Конечно, это предостережение теряет смысл, если социолог не намерен статистически сопоставлять данные, измеренные разными шкалами, и рассматривает их независимо друг от друга, а также в случае иных способов анализа, например, путем множественной классификации.

Второе общее ограничение связано с формой распределения величины фиксированных описанными выше шкалами, которое предполагается нормальным.

На рис. 8 показаны варианты нормального и скошенного распределений, где нормальное (эталонное) обозначено пунктиром, а скошенное — сплошной линией. Нормальное гауссово распределение имеет вид симметричного колокола, у скошенного же по сравнению с нормальным в нашем случае поднят" правый и "опущен" левый конец (так называемые хвосты распределения). Для нормального распределения оценки меры рассеяния совпадают, т. е. М=Ме=Мо, а в скошенном "хвосты" распределения не влияют на среднюю арифметическую (М, другое часто встречающееся обозначение средней арифметической — х), которая сдвигается в сторону его больших значений.

Возможны и бимодальные распределения, где образуются своего рода горбы, а также растянутые, как бы сплющенные. Анализ таких видов распределений должен быть особенно внимательным, так как в этом случае непригодны обычные оценки меры рассеяния.

В случае существенно скошенных и тем более бимодальных распределений можно:

• (а) привести их к нормальному путем объединения градаций шкалы, образующих длинный "хвост" распределения. Например, значения 8,9 и 10 десятибалльной шкалы растянуты потому, что в них очень мало численности. Тогда объединим эти градации и соответственно переоценим пункты шкалы;
• (б) при бимодальном распределении разумно порядковую шкалу перевести в неупорядоченную.

Итак, второе ограничение — особенности одномерных (не говоря уже о более сложных) распределений. Оно заключается в том, что необходимо внимательно изучать форму распределения с точки зрения его уклонения от нормального, симметричного.

Третье ограничение особенно неприятно. Оно состоит в том, что в социальных процессах нередки явления, измерение которых следует производить шкалами открытого типа, где полюс наибольших значений не фиксирован и может принимать любую величину. 17

• 17 На это указал С. Д. Хайтун [277]. См. также работу Г. Кинмбл [110].

Например, оценки размеров заработной платы, доходов в принципе должны давать нормальные и вполне допустимые скошенные распределения, так как есть социально и экономически обоснованные минимум и максимум зарплаты. Это — закрытая метрическая шкала оценок. То же самое можно сказать о численности детей в семье и т. п. явлениях.

Но при оценке многих субъективных состояний и показателей человеческой активности, например, результатов научной продуктивности ученых, предельно максимальные значения трудно предположить достоверно.

В негауссовых, в частности, так называемых распределениях Ципфа (рис. 9, в котором фиксированы логарифмы координат), на примере оценки числа публикаций ученых в области химии [278. С. 146] видно, что до 70% из них имеют одну публикацию, около 25% — две, 8—10% — по три или четыре публикации, но только по 0,1 и 0,2% достигают продуктивности в 20—30 публикациях.

Это распределение никоим образом не описывается гауссовым "колоколом", В последнем случае численность имеющих очень мало и очень много публикаций была бы примерно равной, а большинство ученых демон стрировали бы некоторое среднее число публикаций, например, по 7—8 (в гауссовой статистике — это различные показатели центральной тенденции распределения).

Однако применение негауссовых статистик в социальных науках вообще, в социологии в частности, крайне затруднительно, так как невозможно использовать закрытые шкалы, поскольку в большинстве случаев нет "естественных" эталонов измерения (число публикаций — один из примеров такого "естественного" эталона).

А если нам приходится изобретать шкалу, то недопустимо оставлять открытым один из ее полюсов.

Четвертое ограничение связано с особой природой социальных процессов, в которых статистические и детерминистские закономерности находятся в динамическом единстве. В определенных аспектах и на определенных отрезках времени социальные процессы вполне предсказуемы. Но во многих случаях это далеко не так, особенно в условиях социальных преобразований, кризисов социальных систем. В нестабильных системах малые внешние или внутренние воздействия способны вызвать неожиданное и неадекватное воздействию изменение.

Поэтому предлагается, используя для измерения первичных характеристик шкальные процедуры, прибегать к построению стохастических динамических моделей на основе "сценариев" возможного развития определенных социальных процессов [289]. Такие сценарии прогнозируются для разных временных интервалов, например начальной и завершающей стадий, которые могут быть существенно разными по составу участвующих факторов и по характеру связей между ними.

Итак, преимущества квантификации и использования жестких критериев надежности исходных данных небезусловны и могут обернуться упрощением, а то и искажением социальной реальности. 18

• 18 На почве резкой критики жестко формальных процедур сбора и анализа данных в начале 70-х гг. в социологии возникло движение сторонников гибких или качественных методов с акцентом на понимании событий и жизни людей в большей мере, чем стремления к их строгому объяснению (см. гл. 6).

Адекватные в исследовании массо-видных социальных процессов, такие приемы утрачивают свои достоинства в изучении сознательно организованных действий или "отклоняющихся" явлений, тогда как нередко именно последние дают пищу для вдумчивого социального анализа. Без таких "уклонений" социальные процессы отображаются и виде схем, лишенных жизненных красок.

Строго формализованный количественный анализ имеет свои пределы (298) 19 , за которыми могут быть утрачены качество, глубина и полнота осмысления действительности.

• 19 "Пределы" — так называлась статья выдающегося отечественного социолога В. Н. Шубкина, который в 70-е гг. призвал к "гуманистической социологии", акцентирующей внимание на личностных смыслах социальных явлений и процессов.

Поэтому социолог обязан хорошо владеть многообразными гибкими методами изучения общественных про блем, т. е. уметь наблюдать, строить гипотезы на основе несистематизированных впечатлений и бесед, переходя затем к более систематизированной и упорядоченной их проверке.

Практические советы

1. Приступая к разработке методов и процедур исследования, вначале продумайте, какие явления, свойства и объекты реально варьируют по их интенсивности, распространенности, состояниям выраженности, а какие могут быть фиксированы лишь в качественных отображениях.
2. Определяя способ квантификации (тип шкалы), соизмеряйте его не только с природой объекта, но и с целями исследования и возможностями последующего количественного анализа: излишняя квантификация — напрасная растрата усилий, недостаточная — упущенные возможности более обстоятельного изучения объекта.
3. Не забывайте, что всегда лучше опираться на достоверные и менее детальные сведения, чем на детальные и малодостоверные: отсюда — указания к выбору приемлемого типа шкал и дробности их метрики.
4. Изящный статистический анализ полученных данных будет вводить в заблуждение и нас самих и других, если ему не предшествовала добротная проверка надежности исходных измерений и регистрации фактов в целом.
5. Самое же главное состоит в том, что количественный анализ не самоцель, но лишь средство качественного: качественный анализ предшествует квантификации, качественным анализом завершается изучение количественных распределений и связей.

Содержание

Дальше