Избыточные коды

Московский Технический Университет Связи и Информатики

Кафедра Радиотехнических Систем реферат по избыточным кодам

Преподаватель: Смердова Н. Е.

Группа: РТ 9505

Студент: Матвеев А. Н.

Дата сдачи: Май 1999 года.

Москва, 1999 г.

Вступление.

Известно, что каналы, по которым передается информация, практически никогда не бывают идеальными (каналами без помех). В них почти всегда присутствуют помехи. Отличие лишь в уровне помех и их спектральном составе. Помехи в каналах образуются по различным причинам, но результат воздействия их на передаваемую информацию всегда один тАУ информация теряется (искажается).

Для предотвращения потерь информации в канале были придуманы избыточные коды (коды с избыточностью). Преимущество избыточного кода в том, что при приеме его с искажением (количество искаженных символов зависит от степени избыточности и структуры кода) информация может быть восстановлена на приемнике.

Существуют избыточные коды с обнаружением (они только обнаруживают ошибку) и коды с исправлением (эти коды обнаруживают место ошибки и исправляют ее).

Для различных помех в канале существуют различные по своей структуре и избыточности коды. Обычно избыточность кодов находится в пределах 10тАж60% или чуть больше. Избыточность 1/4 (25%) применяется при записи информации на лазерные диски и в системах цифрового спутникового ТВ.

Классификация кодов.

Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. ПоВнмехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последоваВнтельность элементарных сообщений источника разбивается на отВнрезки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обычВнно кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код.

Длина блока может быть как постоянной, так и переменной. Различают равномерные и неравномерные блочВнные коды. Помехоустойчивые коды являются, как правило, равВнномерными.

Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные символы, несущие инВнформацию о сообщениях и проверочные. Такие коды обозначаВнются как (n, k), где n- длина кода, k- число информационных символов. Число комбинаций в коде не превышает 2^k. К неразделиВнмым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные.

Коды с постоянным весом характеризуются тем, что их кодоВнвые комбинации содержат одинаковое число единиц: Примером такого кода является код тАЬ3 из 7тАЭ, в котором каждая кодовая комбинация содержит три единицы и четыре нуля (стандартных телеграфный код № 3).

Коды с постоянным весом позволяют обнаружить все ошибки кратности q=1,..,n за исключением случаев, когда число едиВнниц, перешедших в нули, равно числу нулей, перешедших в едиВнницы. В полностью асимметричных каналах, в коВнторых имеет место только один вид ошибок (преобразование нуВнлей в единицы или единиц в нули), такой код дозволяет обнаруВнжить все ошибки. В симметричных каналах вероятность необнаВнруженной ошибки можно определить как вероятность одновременного искажения одной единицы и одного нуля:

где Pош вероятность искажения символа.

Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информациВнонными, остальные (n- k) символов тАФ проверочными.

Среди линейных систематических кодов наиболее простой код (n, n-k), содержащий один проверочный символ, коВнторый равен сумме по модулю 2 всех информационных символов. Этот код, называемый кодом с проверкой на четность, позволяет обнаружить все сочетания ошибок нечетной кратности. Вероятность необнаруженной ошибки в первом приближении можно определить как вероятность искажения двух символов:

Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодоВнвыми комбинациями. Это свойство позволяет в значительной стеВнпени упростить кодирующее и декодирующее устройства, особенВнно при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ тАФ коды) и др.

Примером нелинейного кода является код Бергера, у котороВнго проверочные символы представляют двоичную запись числа единиц в последовательности информационных символов. НаприВнмер, таким является код: 00000; 00101; 01001; O111O; 10001; 10110; 11010; 11111. Коды Бергера применяются в асимметВнричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных.

Непрерывные коды характеризуются тем, что операции кодиВнрования и декодирования производятся над непрерывной последоВнвательностью символов без разбиения ее на блоки. Среди непреВнрывных наиболее применимы сверточные коды.

Как известно различают каналы с независимыми и группирующимися ошибками. Соответственно помехоустойчивые коды можно разбить на два класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Далее будут рассматриваться в основном коды, исправляющие независимые ошибки. Это объясняется тем, что хотя для исправления пакетов ошибок разВнработано много эффективных кодов, на практике целесообразнее использовать коды, исправляющие независимые ошибки вместе с устройством перемежения символов или декорреляции ошибок. При этом символы кодовой комбинации не передаются друг за другом, перемешиваются с символами других кодовых комбинаций. ЕсВнли интервал между символами, принадлежащими одной кодовой комбинации, сделать больше чем тАЬпамятьтАЭ канала, то ошибки в пределах кодовой комбинации можно считать независимыми, что и позволяет использовать коды, исправляющие независимые ошибки.

Блочные коды. Построение кодеков.

Линейные коды.

Из определения следует, что любой линейный код (п, k) можВнно получить из k линейно независимых кодовых комбинаций пуВнтем их посимвольного суммирования по модулю 2 в различных сочетаниях. Исходные линейно независимые кодовые комбинаВнции называются базисными.

Представим базисные кодовые комбинации в виде матрицы размерностью nXk

(7.7)

В теории кодирования она называется порождающей. Тогда проВнцесс кодирования заключается в выполнении операции: B=AG,

где А- вектор размерностью k, соответствующий сообщению, В- вектор размерностью п, соответствующий кодовой комбиВннации.

Таким образом, порождающая матрица (7.7) содержит всю неВнобходимую для кодирования информацию. Она должна хранитьВнся в памяти кодирующего устройства. Для двоичного кода объем памяти равен kXn двоичных символов. При табличном задании кода кодирующее устройство должно запоминать

двоичных символов.

Две порождающие матрицы, которые отличаются друг от друВнга только порядком расположения столбцов, задают коды, коВнторые имеют одинаковые расстояния Хэмминга между соответствующими кодовыми комбинациями, а следовательно, одинакоВнвые корректирующие способности. Такие коды называются эквиВнвалентными.

В качестве базисных комбинаций часто выбирают кодовые комбинации, содержащие по одной единице среди информационных символов. При этом порождающую матрицу удается записать в канонической форме (7.8)

где I- единичная kXk подматрица, P-kX(n-k)- подматрица проверочных символов, определяющая свойства кода. Матрица задает систематический код. Можно показать, что для люВнбого линейного кода существует эквивалентный систематический код.

Линейный (п, k) код может быть задан проВнверочной матрицей Н размерности (rХп). При этом комбинация В принадлежит коду только в том случае, если вектор В ортогоВннален всем строкам матрицы Н, т. е. если выполняется равенство (7.9)

где ттАФсимвол транспонирования матрицы. Так как это равенство справедливо для любой кодовой комбинации, то

Каноническая форма матрицы Н имеет вид (7.10)

где P - подматрица, столбцами которой служат строки подматВнрицы Р (7.8), I-единичная rXr подматрица. Подставляя (7.10) в (7.9), можно получать птАФk уравнений вида (7.11)

которые называются уравнениями проверки. Из (7.11) следует, что проверочные символы кодовых комбинаций линейного кода образуются различными линейными комбинациями информациВнонных символов. Единицы в любой j-й строке подматрицы Р, входящей в проверочную матрицу (7.10), указывают, какие информационные символы участвуют в формировании j-го проверочВнного символа.

Очевидно, что линейный (п, k) код можно построить, испольВнзуя уравнения проверки (7.11). При этом первые k символов коВндовой комбинации информационные, а остальные п-k симвоВнлов - проверочные, образуемые в соответствии с (7.11).

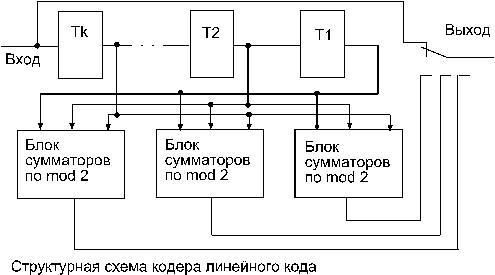
С помощью проверочной матрицы сравнительно легко можно построить код с заданным кодовым расстоянием. Это построение основано на следующей теореме: кодовое расстояние линейВнного (п, k) кода равно d тогда и только тогда, когда любые d-1 столбцов проверочной матрицы этого кода линейно независимы, но некоторые d столбцов проверочной матрицы линейно зависимы.

Заметим, что строки проверочной матрицы линейно независиВнмые. Поэтому проверочную матрицу можно использовать в каВнчестве порождающей для некоторого другого линейного кода (п, п-k), называемого двойственным.

Кодирующее устройство для линейного (п,k) кода (рис. на предыдущей стр.) состоит из k-разрядного сдвигающего регистра и r=п-k блоВнков сумматоров по модулю 2. Информационные символы одноВнвременно поступают на вход регистра и на выход кодирующего устройства через коммутатор К. С поступлением k-го информациВнонного символа на выходах блоков сумматоров в соответствии с уравнениями (7.11) формируются проверочные символы, которые затем последовательно поступают на выход кодера. Процесс декодирования сводится к выполнению операции

, где S тАФ вектор размерностью (п-k), называемый синдромом, В- вектор принятой кодовой комбинации.

Если принятая комбинация В совпадает с одной из разрешенных В (это имеет место тогда, когда либо ошибки в принятых символах отсутствуют, либо из-за действия помех одна разрешенная кодовая комбинация переходит в другую), то

В противном случае SтЙаO, причем вид синдрома зависит только от вектора ошибок е. Действительно,

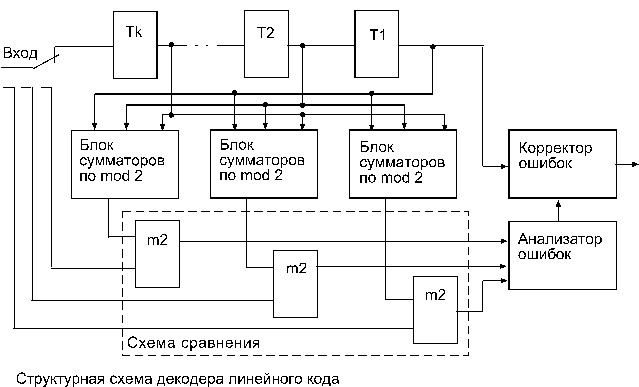
где В- вектор, соответствующий передаваемой кодовой комбиВннации. При S=0 декодер принимает решение об отсутствии ошиВнбок, а при SтЙаO - о наличии ошибок. По конкретному виду синдрома можно в пределах корВнректирующей способности кода указать на ошибочные символы и их исправить.

Декодер линейного кода (рис. на следующей стр.) состоит из k- разрядного сдвигающего регистра, (п-k) блоков сумматоров по модулю 2, схеВнмы сравнения, анализатора ошибок и корректора. Регистр слуВнжит для запоминания информационных символов принятой кодоВнвой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретноВнму виду синдрома, получаемого в результате сравнения формируВнемых на приемной стороне и принятых проверочных символов, опВнределяет места ошибочных символов. Исправление информационВнных символов производится в корректоре. Заметим, что в общем случае при декодировании линейного кода с исправлением ошибок в памяти декодера должна храниться таблица соответствий между синдромами и векторами ошибок. С приходом каждой кодовой комбинаВнции декодер должен перебрать всю таблицу. При небольших знаВнчениях (п-k) эта операция не вызывает затруднений. Однако для высокоэффективных кодов длиной п, равной нескольким десяткам, разность (п-k) принимает такие значения, что перебор таблицы оказывается практически невозможным. Например, для кода (63, 51), имеющего кодовое расстояние d=5, таблица состоит из 2^12 = 4096 строк.

Задача заключается в выборе наилучшего (с позиции тоВнго или иного критерия) кода. Следует заметить, что до сих пор общие методы синтеза оптимальных линейных кодов не разраВнботаны.

Циклические коды.

Циклические коды относятся к классу линейных систематиВнческих. Поэтому для их построения в принципе достаточно знать порождающую матрицу.

Можно указать другой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленаВнми b(х) вида:

где bn-1bn-2..bo - кодовая комбинация. Над данными многоВнчленами можно производить все алгебраические действия с учеВнтом того, что сложение здесь осуществляется по модулю 2.

Каждый циклический код (n, k) характеризуется так назыВнваемым порождающим многочленом. Им может быть любой мноВнгочлен р(х) степени n-k. Циклические коды характеризуются тем, что многочлены b(x) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к отысканию многочлена b(x) по известным многочленам a(х) а р(х), делящегося на р(х), где a(х)- многочлен степени k-1, соответствующий информационВнной последовательности символов.

Очевидно, что в качестве многочлена b(x) можно использоВнвать произведение a(х)р(х). Однако при этом информационные и проверочные символы оказываются перемешанными, что затрудВнняет процесс декодирования. Поэтому на практике в основном применяется следующий метод нахождения многочлена b(x).

Умножим многочлен а(х) на и полученное произведение разделим на р(х). Пусть (7.12)

где m(х)- частное, а с(х)- остаток. Так как операции суммиВнрования и вычитания по модулю 2 совпадают, то выражение (7.12) перепишем в виде: (7.13)

Из (7.13) следует, что многочлен делится на р(х) и, следовательно, является искомым.

Многочлен имеет следующую структуру: первые n-k членов низшего порядка равны нулю, а коэффициенты остальВнных совпадают с соответствующими коэффициентами информаВнционного многочлена а(х). Многочлен с(х) имеет степень меньВнше n-k. Таким образом, в найденном многочлене b(x) коэффициенты при х в степени n-k и выше совпадают с информационВнными символами, а коэффициенты при остальных членах, опреВнделяемых многочленом с(х), совпадают с проверочными симВнволами. На основе приведенных схем умножения и деления многочлеВннов и строятся кодирующие устройства для циклических кодов.

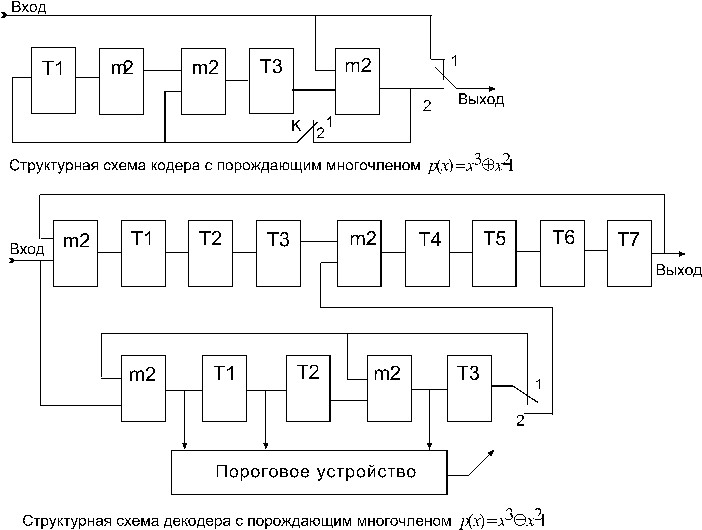
В качестве примера приведена схема кодера и декодера для кода (см. рис.) с порождающим многочленом:

Код имеет кодовое расстояние d=3, что позволяет ему исправВнлять все однократные ошибки.

Принятая кодовая комбинация одновременно поступает в буВнферный регистр сдвига, служащий для запоминания кодовой комВнбинации и для ее циклического сдвига, и на устройство деления на многочлен р(х) для вычисления синдрома. В исходном состоянии ключ находится в положении 1. После семи тактов буферный реВнгистр оказывается загруженным, а в регистре устройства деления будет вычислен синдром. Если вес синдрома больше единицы, то декодер начинает производить циклические сдвиги комбинации в буферном регистре при отсутствии новой комбинации на входе и одновременно вычислять их синдромы s(x)ximodp(x) в устройВнстве деления. Если на некотором 1-м шаге вес синдрома окажетВнся меньше 2, то ключ переходит в положение 2, обратные связи в регистре деления разрываются. При последующих тактах ошибВнки исправляются путем подачи содержимого регистра деления на вход сумматора по модулю 2, включенного в буферный регистр. После семи тактов работы декодера в автономном режиме исВнправленная комбинация в буферном регистре возвращается в исВнходное положение (информационные символы будут занимать старшие разряды).

Существуют и другие, более универсальные, алгоритмы декоВндирования.

К циклическим кодам относятся коды Хэмминга, которые явВнляются примерами немногих известных совершенных кодов. Они имеют кодовое расстояние d=3 и исправляют все одиночные ошибки. Среди циклических кодов широкое применение нашли коды Боуза- Чоудхури- Хоквингема (БЧХ).

Сверточные коды

Методы описания сверточных кодов.

Кодер СК содержит регистр памяти для хранения опредеВнленного числа информационных символов и преобразователь информационной последовательности в кодовую последовательность. Процесс кодирования производится непрерывно. Скорость кода R=k/n, где k - число информационных символов, одновременно поступающих на вход кодера, n - число соответствующих им символов на выходе кодера. Схема простого кодера показана на рис. 1.1а.

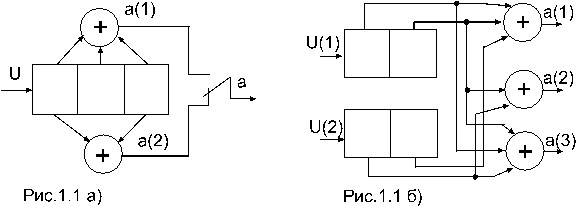
Информационные двоичные символы u поступают на вход регистра с К разрядами. На выходах сумматоров по модулю 2 образуются коВндовые символы a(1) и a(2). Входы сумматоров соединены с определенными разрядами регистра. За время одного инВнформационного символа на выходе обраВнзуются два кодовых символа (R= 1/2). Возможно кодирование и с другими скоростями. При скорости 2/3 на вход кодера одновременно поступает k=2 информационных символа, на выходе при этом образуется n=3 кодовых символа. Схема такого кодера показана на рис. 1.1,6.

Рассматриваемый код называется сверточным, постольку последовательВнность кодовых символов а может быть определена как свертка информационных символов u с импульсным откликом кодера. На рис. 1.2 показано прохождеВнние единичной последовательности u=100тАж через кодер.

Символы a(1) и a(2) на его выходе образуют импульсный откВнлик h= 00111011 00.. Таким образом, если на входе кодера действует произвольная информационная последовательВнность и, то последовательность на его выходе есть сумма по модулю 2 всех импульсных откликов, обусловленных действием смещенных во времени символов 1. Сверточный кодер, как автомат с конечным числом состояВнний, может быть описан диагВнраммой состояний. Диаграмма представляет собой направленВнный граф и описывает все возВнможные переходы кодера из одВнного состояния в другое, а такВнже содержит символы выходов кодера, которые сопровождаВнют эти переходы.

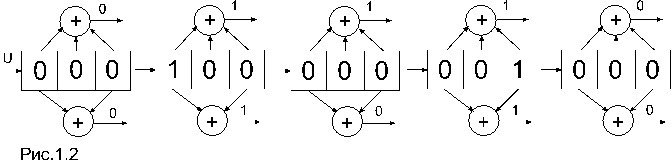
Первоначально кодер находится в состоянии 00, и поступление на его вход информационного символа u=0 перевозят его также в состояние 00. При этом на выходе кодера будут символы a(1)a(2)=00. На диаграмме этот переход обознаВнчается петлей 00, выходящей из состояния 00 и вновь возвращающейся в это состояние. Далее, при поступлении символа u=1 кодер переходит в состояние 10, при этом, на выходе будут символы a(1)a(2)=11. Этот переход из состояния 00 в состояние 10 обозначается пунктирной линией. Далее возВнможно поступление на вход кодера информационных симвоВнлов 0 либо 1. При этом кодер переходит в состояние 01 либо 11, а символы на выходе будут 10 либо 01 соответственВнно. Процесс построения диаграммы заканчивается когда буВндут просмотрены все возможные переходы из одного состояВнния во все остальные.

Решетчатая диаграмма является разверткой диаграммы состояний во времени. На решетке состояния показаны узлами, а пеВнреходы соединяющими их линиями. После каждого переВнхода из одного состояния в другое происходит смещение на один шаг вправо. Решетчатая диаграмма дает наглядное представление всех разрешенных путей, по которым может продвигаться кодер при кодировании. Каждой информационВнной последовательности на входе кодера соответствует единВнственный путь по решетке. Построение решетки производится на основе диаграммы состояний. Исходное состояние S(1)S(2)=0. С поступлением очередного символа u=0 либо 1 возВнможны переходы в состояния 00 либо 10, обозначаемые ветВнвями 00 и 11. Процесс следует продолжить, причем через три шага очередной фрагмент, решетки будет повторяться. Пунктиром показан путь 11100001.., соответствующий поВнступлению на вход кодера информационной последовательности 1011..

Для описания кодера последовательности символов на его входе и выходе представляют с использованием оператора задержки:

Здесь индексы в скобках обозначают: i- номер входа кодеВнра, 1тЙд jтЙд n, j- номер выхода кодера, 1тЙдiтЙд k. Индексы без скобок (0, 1, 2, ..) обозначают дискретные моменты времени.

Процесс кодирования может быть представлен как умножение многочлена входной информационной последовательВнности u(D) на порождающие многочлены кода G(j)(D), котоВнрые описывают связи ячеек регистра кодера с его выходами (1.1):

Порождающий многочлен представим в виде ряда (1.2):

СК можно также задавать порождающей матрицей (1.3):

Порождающая матрица состоит из сдвигов базисной поВнрождающей матрицы (верхняя строка матрицы О), которая, в свею очередь, состоит из элементарВнных матриц Gi, 0тЙдiтЙдk-1, содержащих k строк и n столбВнцов. Элементами этих матриц двоичных кодов являются симВнволы 0 и 1.

Как при использовании блоковых кодов, процесс кодирования может быть представлен в матричной форме: A=UG (1.4)

,где U- полубесконечная матрица входных информационных символов, А- полубесконечная матрица символов на выходе кодера.

Декодирование сверточных кодов.

Алгебраические методы декодирования основаны на исВнпользовании алгебраических свойств кодовых последовательВнностей. В ряде случаев эти методы приводят к простым реаВнлизациям кодека. Такие алгоритмы являются неоптимальными, так как используемые алгебраические процедуры декодирования предназначены для исправления конкретных (и не всех) конфигураций ошибок в канале. Алгебраические методы отождествляют с поэлементным приемом последоВнвательностей, который для кодов с избыточностью, как известно, дает худшие результаты, чем прием в целом.

Вероятностные методы декодирования значительно ближе к оптимальному приему в целом, так как в этом случае деВнкодер оперирует с величинами, пропорциональными вероятВнностям, оценивает и сравнивает вероятности различных гиВнпотез и на этой основе выносит решения о передаваемых симВнволах.

Пороговое декодирование.

Вероятностные методы декодирования достаточно сложны в реализации, хотя и обеспечивают высокую помехоустойчиВнвость. Наряду с ними широко применяют более простые алВнгоритмы. Для этой цели используют класс СК, допускающих пороговое декодирование.

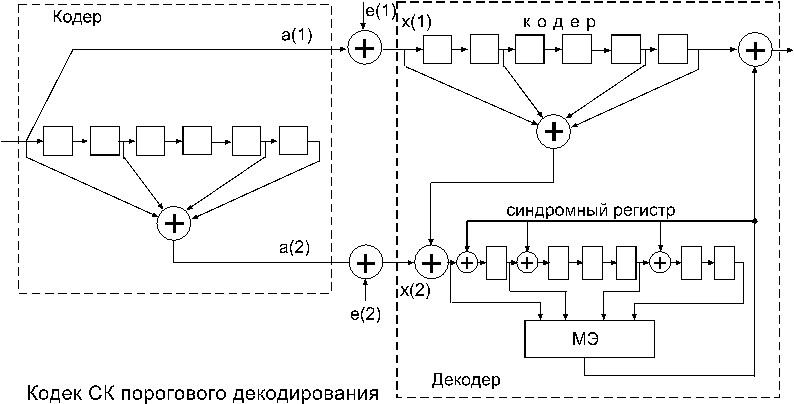
Рассмотрим систематический код со скоростью 1/2 и мноВнгочленами:

Схема кодека на рисунке. Моделью двоичного канала являются сумматоры по

модулю 2, на входы которых, кроме кодовых последовательностей а(1) и а(2), поступают ошибки е(1) и е(2). Декодер содержит аналог кодера, в котором принятым символам формируется копия проверочной последовательности. В формирователе синдрома (сумматоре по модуВнлю 2) образуется последовательность синдромов, которая поступает на вход синдромного регистра. Наборам ошибок соответствуют определенные конфигурации синдромов последовательности S. Если количество ненулевых синдромов превышает определенный порог, на выходе порогового элемента появляется символ коррекции, который в корректоре испольВнзуется для исправления ошибки в информационном символе.

Список использованной литературы:

Радиотехнические системы передачи информации, под ред. В. В. Калмыкова
Сверточные коды в системах передачи информации, учебное пособие

Вместе с этим смотрят:

Измерение больших линейных геометрических размеров
Измерение низких температур
Измерение параметров АЦП
Изучение и исследование интегрированных RS-триггеров, а также триггеров серии К155