Метод экспертных оценок
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Экономический факультет
Кафедра антикризисного управления, оценки бизнеса и инноваций
МЕТОД ЭКСПЕРТНЫХ ОЦЕНОК
(курсовая работа)
Выполнила студентка
3 курса, группа 277
Стрекалова С.Б.
Научный руководитель
Киселева Н.М.
Работа защищена
1999г.
Оценка
Барнаул тАУ 1999
СОДЕРЖАНИЕ
Введение 3
Глава 1. ЭКСПЕРТИЗА В УПРАВЛЕНИИ 5
1.1. Роль экспертов в управлении 5
1.2. Метод экспертных оценок 7
1.3. Организация экспертного оценивания 9
1.4. Подбор экспертов 9
1.5. Опрос экспертов 10
Глава 2. ФОРМАЛИЗАЦИЯ ИНФРОРМАЦИИ
И ШКАЛЫ СРАВНЕНИЙ 12
Глава 3. ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК 16
3.1. Задачи обработки 16
3.2. Групповая оценка объектов 17
3.3. Оценка согласованности мнений экспертов 22
3.4. Обработка парных сравнений объектов 25
3.5. Определение взаимосвязи ранжировок 27
Заключение 31
Список литературы 32
ВВЕДЕНИЕ
Современная экономика предъявляет новые, более высокие требования к управлению. Вопросы совершенствования методов управления приобретают сейчас очень важное значение, поскольку именно в этой сфере имеются еще большие резервы роста эффективности народного хозяйства.
Существенным фактором повышения научного уровня управления является применение при подготовке решений математических методов и моделей. Однако, полная математическая формализация технико-экономических задач часто неосуществима вследствие их качественной новизны и сложности. В связи с этим все шире используются экспертные методы, под которыми понимают комплекс логических и математико-статистических методов и процедур, направленных на получение от специалистов информации, необходимой для подготовки и выбора рациональных решений.
Экспертные методы применяют сейчас в ситуациях, когда выбор, обоснование и оценка последствий решений не могут быть выполнены на основе точных расчетов. Такие ситуации нередко возникают при разработке современных проблем управления общественным производством и, особенно, при прогнозировании и долгосрочном планировании. В последние годы экспертные оценки находят широВнкое применение в социально-политическом и научно-техВнническом прогнозировании, в планировании народного хозяйства, отраслей, объединений, в разработке крупных научно-технических, экономических и социальных проВнграмм, в решении отдельных проблем управления.
В ходе развития общественного производства возрастают не только сложность управления, но и требования к качеству принимаемых решений. Для того, чтобы повысить обоснованность решений и учесть многочисленные факторы, оказывающие влияние на их результаты, необходим разносторонний анализ, основанный как на расчетах, так и на аргументированных суждениях руководителей и специалистов, знакомых с состоянием дел и перспективами развития в различных областях практической деятельности. Применение экспертных методов обеспечивает активное и целенаправленное участие специалистов на всех этапах принятия решений, что позволяет существенно повысить их качество и эффективность.
Целью нашей работы является изучение метода экспертных оценок - одного из важнейших этапов принятия грамотных управленческих решений.
Задачи:
- изучение роли экспертизы в управлении;
- рассмотрение порядка организации экспертного оценивания;
- изучение видов шкал и порядка их использования;
- подробное рассмотрение заключительного этапа экспертного оценивания тАУ обработки экспертных оценок.
Реферат состоит из введения, трех глав, заключения и списка использованной литературы.
В первой главе рассматривается вопрос о необходимости экспертизы в управлении, рассмотрен метод экспертных оценок, этапы организации экспертного оценивания.
Вторая глава посвящена рассмотрению шкал сравнений, даны характеристики каждому виду шкал и порядок их использования при формализации информации.
В третьей главе рассматривается обработка экспертных оценок: задачи обработки, групповая оценка объектов, оценка согласованности мнений экспертов, обработка парных сравнений объектов и определение взаимосвязи ранжировок.
Так как целью данной работы является рассмотрение экспертного оценивания в теоретическом аспекте, то практическое применение не рассматривается.
В заключении рассматривается роль метода экспертных оценок в принятии управленческих решений.
Глава 1. ЭКСПЕРТИЗА В УПРАВЛЕНИИ
Роль экспертов в управлении
Современное общество развивается под постоянно усиливающимся воздействием научно-технической революции, которая вызывает коренные преобразования в производстве, глубокие изменения в структуре и экономике народного хозяйства. Происходящая научно-техническая революция по своему влиянию далеко выходит за пределы сферы материального производства, захватывая все стороны жизнедеятельности общества, предопределяя большинство решений, направленных на его рациональное экономическое и социальное развитие.
История развития науки, техники и производства показывает, что одновременно с последовательным замещением функций человека функциями машин увеличивается его роль в сфере управления. Непрерывный рост объема затрат на развитие науки, на создание новой техники и совершенствование производства существенно повышает значимость решений, принимаемых на всех уровнях управления народным хозяйством. Будущее науки. Техники и экономики в значительной мере зависит от качества и своевременности этих решений, а объективные тенденции научно-технического прогресса могут ускоряться или замедляться под их воздействием.
Особое значение в управлении сейчас приобретают методы оптимизации, основанные на применении формальных, чаще всего математических моделей, обеспечивающих экономию времени и средств при решении многих практических задач. Построение моделей помогает привести сложные и подчас неопределенные факторы, связанные с проблемой принятия решений, в логически стройную схему, определить, какие данные необходимы для оценки и выбора альтернатив.
В процессе управления возникает естественное стремление к отысканию решения, которое объективно является наилучшим из всех возможных. В качестве инструмента оптимизации сейчас широко используется математическое программирование. Успехи в применении математического программирования к решению различного рода хозяйственных, научных, технических и военных задач породили методологические воззрения, согласно которым кардинальное решение проблем управления возможно только тогда, когда все его аспекты отображаются в системе взаимосвязанных математических моделей.
Однако, формализация технико-экономических и управленческих решений осложняется рядом особенностей современного этапа научно-технического прогресса. Жизнь общества настолько сложна, что трудно рассчитывать на появление моделей, которые полностью отражали бы природу и количественные взаимосвязи социально-экономических процессов. Реальная действительность всегда сложнее самых тонких математических моделей, а ее развитие часто опережает формальное познание. Задачи управления требуют в качестве неотъемлемого элемента решения участия людей. И, наконец, сам процесс управления всегда предполагает ориентацию не только на числовые данные, но и на обычный здравый смысл. Использование математического программирования и вычислительной техники позволяет принимать решения, основанные на более полной и надежной информации. Но, несомненно и то, что при любых условиях для выбора рационального решения требуется нечто большее, чем хорошая математическая модель.
Принимая решения, мы обычно предполагаем, что информация, используемая для их обоснования, достоверно и надежна. Но для многих экономических и научно-технических задач, являющихся по своему характеру качественно новыми и неповторяющимися, это предположение либо заведомо не реализуется, либо в момент принятия решения его не удается доказать.
Наличие информации и правильность ее использования в значительной степени предопределяют оптимальность выбранного решения. Кроме данных, состоящих из числовых статистических величин, информация включает в себя другие, не поддающиеся непосредственному измерению величины, например, предположения о возможных решениях и их результатах. Практика показывает, что основные трудности, возникающие при поиске и выборе деловых решений, обусловлены прежде всего недостаточно высоким качеством и неполнотой имеющейся информации.
Основные трудности, связанные с информацией, возникающие при выработке сложных решений, можно подразделить на следующие группы.
Во-первых, исходная статистическая информация зачастую бывает недостаточно достоверной.
Во-вторых, некоторая часть информации имеет качественный характер и не поддается количественной оценке. Так, нельзя точно рассчитать степень влияния социальных и политических факторов на реализацию планов, оценить экономический эффект будущих изобретений и т.д. Но, поскольку эти факторы и явления оказывают существенное влияние на результаты решений, их нельзя не учитывать.
В-третьих, в процессе подготовки решений часто возникают ситуации, когда в принципе необходимую информацию получить можно, однако в момент принятия решения она отсутствует, поскольку это связано с большими затратами времени или средств.
В-четвертых, существует большая группа факторов, которые могут повлиять на реализацию решения в будущем, но их нельзя точно предсказать.
В-пятых, одна из наиболее существенных трудностей при выборе решений состоит в том, что любая научная или техническая идея содержит в себе потенциальную возможность различных схем ее реализации, а любое экономическое действие может приводить к многочисленным исходам. Проблема выбора наилучшего варианта решения может возникнуть и потому, что обычно существуют ограничения в ресурсах, а следовательно, принятие одного варианта всегда связано с отказом от других решений.
В-шестых, при выборе наилучшего решения мы нередко сталкиваемся с многозначностью обобщенного критерия, на основе которого можно произвести сравнение возможных исходов. Многозначность, многомерность и качественное различие показателей являются серьезным препятствием для получения обобщенной оценки относительной эффективности, важности, ценности или полезности каждого из возможных решений.
В связи с этим одна из главных особенностей решения сложных проблем состоит в том, что применение расчетов здесь всегда переплетается с использованием суждений руководителей, ученых, специалистов. Эти суждения позволяют хотя бы частично компенсировать недостаток информации, полнее использовать индивидуальный и коллективный опыт, учесть предположения специалистов о будущих состояниях объектов. Закономерность развития науки и техники состоит в том, что новые знания, научно-техническая информация накапливаются в течение длительного периода времени. Нередко это накопление идет в скрытой форме в сознании ученых и разработчиков. Они, как никто другой, способны оценить перспективы той области, в которой работают, и предвидеть характеристики тех систем, в создании которых непосредственно участвуют.
Опыт показывает, что использование несистематизированных суждений отдельных специалистов оказывается при решении многих сложных научных и технических проблем недостаточно эффективным вследствие многообразия взаимосвязей между основными элементами таких проблем и невозможности охвата их всех. При использовании традиционных процедур подготовки решений нередко не удается рассмотреть широкий диапазон факторов, учесть весь спектр альтернативных путей решения проблем.
Все это заставляет прибегать к комплектованию групп специалистов, представляющих в качестве экспертов различные области знаний. Применение групповой экспертизы позволяет не только рассмотреть множество аспектов и факторов, но и объединить различные подходы, с помощью которых руководитель находит наилучшее решение.
1.2. Метод экспертных оценок
Сущность метода экспертных оценок заключается в проВнведении экспертами интуитивно-логического анализа проблемы с количественной оценкой суждений и форВнмальной обработкой результатов. Получаемое в резульВнтате обработки обобщенное мнение экспертов принимаВнется как решение проблемы. Комплексное использование интуиции (неосознанного мышления), логического мышВнления и количественных оценок с их формальной обраВнботкой позволяет получить эффективное решение пробВнлемы.
При выполнении своей роли в процессе управления эксперты производят две основные функции: формируют объекты (альтернативные ситуации, цели, решения и т. п.) и производят измерение их характеристик (веВнроятности свершения событий, коэффициенты значимоВнсти целей, предпочтения решений и т. п.). Формирование объектов осуществляется экспертами на основе логичеВнского мышления и интуиции. При этом большую роль играют знания и опыт эксперта. Измерение характериВнстик объектов требует от экспертов знания теории измеВнрений.
Характерными особенностями метода экспертных оцеВннок как научного инструмента решения сложных нефорВнмализуемых проблем являются, во-первых, научно обоВнснованная организация проведения всех этапов эксперВнтизы, обеспечивающая наибольшую эффективность работы на каждом из этапов, и, во-вторых, применение коВнличественных методов как при организации экспертизы, так и при оценке суждений экспертов и формальной групповой обработке результатов. Эти две особенности отличают метод экспертных оценок от обычной давно изВнвестной экспертизы, широко применяемой в различных сферах человеческой деятельности.
Экспертные коллективные оценки широко использоВнвались в государственном масштабе для решения сложВнных проблем управления народным хозяйством уже в первые годы Советской власти. В 1918 году при Высшем совете народного хозяйства был создан Совет экспертов, задачей которого являлось решение наиболее сложных проблем реорганиВнзации народного хозяйства страны. При составлении пятилетних планов развития народного хозяйства страны систематически использовались экспертные оценки шиВнрокого круга специалистов.
В настоящее время в нашей стране и за рубежом меВнтод экспертных оценок широко применяется для решения важных проблем различного характера. В различных отраслях, объединениях и на предприятиях действуют постоянные или временные экспертные коВнмиссии, формирующие решения по различным сложным неформализуемым проблемам.
Все множество плохо формализуемых проблем условВнно можно разделить на два класса. К первому классу относятся проблемы, в отношении которых имеется доВнстаточный информационный потенциал, позволяющий успешно решать эти проблемы. Основные трудности в решении проблем первого класса при экспертной оценке заключаются в реализации существующего информациВнонного потенциала путем подбора экспертов, построения рациональных процедур опроса и применения оптимальных методов обработки его результатов. При этом методы опроса и обработки основываются на использовании принципа ВлхорошегоВ» измерителя. Данный принцип означает, что выполняются следующие гипотезы:
1) эксперт является хранилищем большого объема раВнционально обработанной информации, и поэтому он моВнжет рассматриваться как качественный источник инфорВнмации;
2) групповое мнение экспертов близко к истинному реВншению проблемы.
Если эти гипотезы верны, то для построения процеВндур опроса и алгоритмов обработки можно использовать результаты теории измерений и математической статиВнстики.
Ко второму классу относятся проблемы, в отношении которых информационный потенциал знаний недостаточен для уверенности в справедливости указанных гипотез. При решении проблем из этого класса экспертов уже нельзя рассматривать как Влхороших измерителейВ». Поэтому необходимо очень осторожно проводить обработку результатов экспертизы. Применение методов осреднения, справедливых для Влхороших измерителейВ», в данном случае может привести к большим ошибкам. Например, мнение одного эксперта, сильно отличающееВнся от мнений остальных экспертов, может оказаться правильным. В связи с этим для проблем второго класса в основном должна применяться качественная обработВнка.
Область применения метода экспертных оценок весьВнма широка. Перечислим типовые задачи, решаемые меВнтодом экспертных оценок:
1) составление перечня возможных событий в различВнных областях за определенный промежуток времени;
2) определение наиболее вероятных интервалов времеВнни свершения совокупности событий;
3) определение целей и задач управления с упорядочеВннием их по степени важности;
4) определение альтернативных (вариантов решения заВндачи с оценкой их предпочтения;
5) альтернативное распределение ресурсов для решения задач с оценкой их предпочтительности;
6) альтернативные варианты принятия решений в опреВнделенной ситуации с оценкой их предпочтительности.
Для решения перечисленных типовых задач в настояВнщее время применяются различные разновидности метоВнда экспертных оценок. К основным видам относятся: анВнкетирование и интервьюирование; мозговой штурм; дисВнкуссия; совещание; оперативная игра; сценарий.
Каждый из этих видов экспертного оценивания облаВндает своими преимуществами и недостатками, определяВнющими рациональную область применения. Во многих случаях наибольший эффект дает комплексное применеВнние нескольких видов экспертизы.
Анкетирование и сценарий предполагают индивидуВнальную работу эксперта. Интервьюирование может осуВнществляться как индивидуально, так и с группой эксперВнтов. Остальные виды экспертизы предполагают коллекВнтивное участие экспертов, в работе. Независимо от индивидуального или группового участия экспертов в раВнботе целесообразно получать информацию от множества экспертов. Это позволяет получить на основе обработки данных более достоверные результаты, а также новую информацию о зависимости явлений, событий, фактов, суждений экспертов, не содержащуюся в явном виде в высказываниях экспертов.
При использовании метода экспертных оценок возВнникают свои проблемы. Основными из них являются: подбор экспертов, проведение опроса экспертов, обраВнботка результатов опроса, организация процедур эксперВнтизы.
1.3. Организация экспертного оценивания
Первым этапом организации работ по применению эксВнпертного оценивания является подготовка и издание руВнководящего документа, в котором формулируется цель работы и основные положения по ее выполнению. В этом документе должны быть отражены следующие вопросы: постановка задачи-эксперимента; цели эксперимента; обоснование необходимости эксперимента; сроки выполнения работ; задачи и состав группы управления; обязанности и права группы; финансовое и материальное обеспечение работ.
Для подготовки этого документа, а также для рукоВнводства всей работой назначается руководитель экспертизы. На него возлагается формирование группы управВнления и ответственность за организацию ее работы.
После формирования группа управления осуществляВнет работу по подбору экспертной группы примерно в таВнкой последовательности: уяснение решаемой проблемы; определение круга областей деятельности, связанных с проблемой; определение долевого состава экспертов по каждой области деятельности; определение количества экспертов в группе; составление предварительного спиВнска экспертов с учетом их местонахождения; анализ каВнчеств экспертов и уточнение списка экспертов в группе; получение согласия экспертов на участие в работе; составление окончательного списка экспертной группы.
Параллельно с процессом формирования группы экспертов группа управления проводит разработку организации и методики проведения опроса экспертов. При этом решаются следующие вопросы: место и время проведения опроса; количество и задачи туров опроса; форма проведения опроса; порядок фиксации и сбора результатов опроса; состав необходимых документов.
Следующим этапом работы группы управления является определение организации и методики обработки данных опроса. На данном этапе необходимо определить задачи и сроки обработки, процедуры и алгоритмы обВнработки, силы и средства для проведения обработки.
В процессе непосредственного проведения опроса эксВнпертов и обработки его результатов группа управления осуществляет выполнение комплекса работ в соответстВнвии с разработанным планом, корректируя его по мере необходимости по содержанию, срокам и обеспечению ресурсами.
Последним этапом работ для группы управления явВнляется оформление результатов работы. На этом этапе производится анализ результатов экспертного оцениваВнния; составление отчета; обсуждение и одобрение реВнзультатов; представление итогов работы на утверждеВнние; ознакомление с результатами экспертизы организаВнций и лиц.
1.4. Подбор экспертов
Для реализации процедуры экспертного оценивания неВнобходимо сформировать группу экспертов. Общим треВнбованием при формировании группы экспертов является эффективное решение проблемы экспертизы. ЭффективВнность решения проблемы определяется характеристикаВнми достоверности экспертизы и затрат на нее.
Достоверность экспертного оценивания может быть определена только на основе практического решения проблемы и анализа ее результатов. Использование эксВнпертов как раз и обусловлено тем, что отсутствуют каВнкие-либо другие способы получения информации. ПоэтоВнму оценка достоверности экспертизы может осуществВнляться, как правило, только по апостериорным (послеопытным) данным. Если экспертиза проводится систематически с примерно одним и тем же составам экспертов, то появляется возможность накопления стаВнтистических данных по достоверности работы группы экспертов и получения устойчивой числовой оценки доВнстоверности. Эту оценку можно использовать в качестве априорных данных о достоверности группы экспертов для последующих экспертиз.
Достоверность группового экспертного оценивания зависит от общего числа экспертов в группе, долевого состава различных специалистов в группе, от характеВнристик экспертов.
Определение характера зависимости достоверности от перечисленных факторов является еще одной проблеВнмой процедуры подбора экспертов.
Сложной проблемой процедуры подбора является формирование системы характеристик эксперта, сущестВнвенно влияющих на ход и результаты экспертизы. Эти характеристики должны описывать специфические свойВнства специалиста и возможные отношения между людьВнми, влияющие на экспертизу. Важным требованием к характеристикам эксперта является измеримость этих характеристик.
Еще одной проблемой является организация процедуВнры подбора экспертов, т.е. определение четкой последоВнвательности работ, выполняемых в процессе подбора эксВнпертов и необходимых ресурсов для их реализации.
Максимальное число экспертов в группе проверяется на ограничение по финансовым ресурсам. Определив заВнвисимость между достоверностью, количеством эксперВнтов и расходами на оплату, группа управления представВнляет руководству эту информацию и формулирует возВнможные альтернативы решений. Такими альтернативами могут быть либо снижение достоверности результатов экспертного оценивания до уровня, обеспечивающего выВнполнение ограничения по расходам на оплату экспертов, либо сохранение исходного требования на достоверность экспертизы и увеличение расходов на оплату экспертов.
Следующим этапом работы по подбору экспертов явВнляется составление предварительного списка экспертов. При составлении этого списка проводится анализ каВнчеств экспертов. Кроме учета качеств экспертов, опредеВнляются их местонахождение и возможности участия выВнбранных специалистов в экспертизе. При оценке качеств учитывается мнение людей, хорошо знающих кандидаВнтов в эксперты.
После составления списка экспертов им направляютВнся письма с приглашением участвовать в экспертизе. В письмах объясняется цель проведения экспертизы, ее сроки, порядок проведения, объем работы и условия вознаграждения. К письмам прилагаются анкеты данных эксперта и самооценки компетентности. Получив ответы экспертов, группа управления составВнляет окончательный список группы экспертов.
После составления и утверждения списка экспертам посылается сообщение о включении их в состав экспертВнной группы. Если экспертное оценивание производится методом анкетирования, то одновременно с уведомлением о включении в экспертную группу всем экспертам высыВнлается анкета с необходимыми инструкциями для их заВнполнения. Сообщением экспертам о включении их в эксВнпертизу заканчивается работа по подбору экспертов.
1.5. Опрос экспертов
Опрос тАУ главный этап совместной работы группы управВнления и экспертов. Основным содержанием опроса являВнется:
- постановка задачи и предъявление вопросов эксперВнтам;
- информационное обеспечение работы экспертов;
- выработка экспертами суждений, оценок, предложеВнний;
- сбор результатов работы экспертов.
Можно назвать три типа задач, которые решаются в процессе опроса:
- оценка качественная или количественная заданных объектов;
- построение новых объектов;
- построение и оценка новых объектов.
При коллективной экспертизе используются следуюВнщие основные виды опроса: дискуссия, анкетирование и интервьюирование, метод коллективной генерации идей, или мозговой штурм.
Анкетирование может проводиться с обратной связью или без нее. При анкетировании с обратной связью опрос эксперВнтов производится в несколько этапов с доведением до сведения экспертов некоторых результатов опроса на предыдущем этапе, включая оценки отдельных экспертов и их аргументацию.
Главным в организации опроса является обеспечение максимума информации и максимума творческой активВнности, самостоятельности эксперта. Необходимо стреВнмиться довести до каждого эксперта по возможности всю информацию, относящуюся к анализируемому явВнлению, которой располагают как эксперты, так и оргаВннизаторы опроса, не лишая в то же время эксперта творВнческой самостоятельности и активности.
Однако возможности эксперта по переработке инфорВнмации ограниченны. В результате эксперт может принять решение, не используя всей информации, имеющейся в его распоряжении. Кроме того, новая информация воспринимается челоВнвеком с определенным внутренним сопротивлением и не сразу влияет на уже сложившиеся субъективные оценки. Отношение к новой информации благожелательнее, а восприятие и использование ее полнее, если она предВнставляется в доходчивой, яркой и компактной форме.
Из этих психологических особенностей следует необВнходимость предоставления экспертам возможностей для фиксации поступающей информации путем ведения заВнписей, использования технических средств, а также неВнобходимость предварительной обработки информации и представления ее экспертам в наиболее воспринимаемой форме.
Необходимо подчеркнуть противоречивость значения обмена экспертами информацией, так как получение такой информации таит опасность потери творческой неВнзависимости в построении модели объекта экспертом. Разрешение этого противоречия в полной мере невозВнможно, и при каждой экспертизе ее организаторы должВнны находить разумный компромисс, прежде всего, путем выбора вида опроса, формы и степени общения эксперВнтов.
Каждый из видов опроса имеет свои достоинства и недостатки в построении обмена информацией между экспертами и в организации их независимого творчества. Выбор того или иного вида опроса определяется многиВнми факторами, из которых основными являются:
- цель и задачи экспертизы;
- существо и сложность анализируемой проблемы;
- полнота и достоверность исходной информации;
- требуемые объем и достоверность информации, полуВнчаемой в результате опроса;
- время, отведенное на опрос и экспертизу в целом;
- допустимая стоимость опроса, и экспертизы в целом;
- количество экспертов и членов группы управления, их характеристики.
Анкетирование является наиболее эффективным и самым распространенным видом опроса, ибо позволяет наилучшим образом сочетать информационное обеспечеВнние экспертов с их самостоятельным творчеством.
Глава 2. ФОРМАЛИЗАЦИЯ ИНФОРМАЦИИ И ШКАЛЫ СРАВНЕНИЙ
Рациональное использование информации, полученной от экспертов, возможно при условии образования ее в форму, удобную для дальнейшего анализа, направленного на подготовку и принятие решений.
Возможности формализации информации зависят от специфических особенностей исследуемого объекта, надежности и полноты имеющихся данных, уровня принятия решения. Форма представления экспертных данных зависит и от принятого критерия, на выбор которого, в свою очередь, существенное влияние оказывает специфика исследуемой проблемы.
Формализация информации, полученной от экспертов, должна быть направлена на подготовку решения таких технико-экономических и хозяйственных задач, которые не могут быть в полной мере описаны математически, поскольку являются ВлслабоструктуризованнымиВ», т.е. содержат неопределенности, связанные не только с измерением, но и самим характером исследуемых целей, средств их достижения и внешних условий.
При анализе перспектив необходимо не только представить в виде косвенных оценок часть информации, не поддающуюся количественному измерению, и не только выразить с помощью таких оценок количественно измеримую информацию, о которой в момент подготовки решения нет достаточно надежных данных. Самое важное тАУ формализовать эту информацию так, чтобы помочь принимающему решение выбрать из множества действий одно или несколько, наиболее предпочтительные в отношении некоторого критерия.
Если эксперт в состоянии сравнить и оценить возможные варианты действий, приписав каждому из них определенное число, значит, он обладает определенной системой предпочтений. В зависимости от того, по какой шкале могут быть заданы эти предпочтения, экспертные оценки содержат больший или меньший объем информации и обладают различной способностью к формализации.
Исследуемые объекты или явления можно опознавать или различать на основе признаков или факторов. Фактор тАУ это множество, состоящее, по крайней мере, из двух элементов, отражающих различные уровни некоторых подлежащих рассмотрению величин. Уровень одних факторов может быть выражен количественно (в рублях, процентах, килограммах и т.д.) тАУ такие факторы называются количественными. Уровень других нельзя выразить с помощью числа, их называют качественными.
Факторы условно разделяют на дискретные и непрерывные. Дискретными являются факторы с определенным, обычно небольшим, числом уровней. Факторы, уровни которых рассматриваются как образующие непрерывное множество, называют непрерывными. В зависимости от целей и возможностей анализа одни и те же факторы могут трактоваться или как дискретные, или как непрерывные.
Рассмотрим основные логические аксиомы, которые используются в эксперных методах при формализации информации с помощью различных шкал.
При использовании номинальных шкал исследуемые объекты можно опознавать и различать на основе трех аксиом идентификации [6]:
- i либо есть j, либо есть не j;
- если i есть j, то j есть i;
- если i есть j и j есть k, то i есть k.
Факторы в данном случае выступают как ассоциативные показатели, обладающие информацией, которая может быть формализована в виде бинарных оценок двух уровней: 1 (идентичен) или 0 (различен).
В случаях, когда исследуемые объекты можно в результате сравнения расположить в определенной последовательности с учетом какого-либо существенного фактора (факторов), используются порядковые шкалы, позволяющие устанавливать равноценность или доминирование.
Предположим, что необходимо расположить в определенной последовательности n объектов по какому-либо фактору (критерию). Представим это упорядочение в виде матрицы 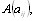 где i, j = 1,2,тАж, n.
где i, j = 1,2,тАж, n.
Величины 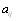 устанавливают соотношения между объектами и могут быть определены следующим образом [6]:
устанавливают соотношения между объектами и могут быть определены следующим образом [6]:
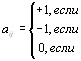
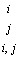

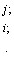
Установим основные аксиомы, необходимые для соблюдения условий упорядочения. Соотношение 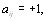 означающее, что i предпочтительнее j, должно быть ассиметричным, т.е., если
означающее, что i предпочтительнее j, должно быть ассиметричным, т.е., если 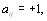 то
то 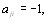 и транзитивным, т.е., если
и транзитивным, т.е., если 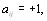
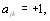 то
то 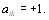
Соотношение 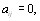 означающее, что i и j равноценны, называется соотношением эквивалентности. Такое соотношение должно быть
означающее, что i и j равноценны, называется соотношением эквивалентности. Такое соотношение должно быть
рефлексивным, т.е. 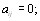
симметричным, т.е., если 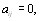 то
то 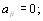
транзитивным, т.е., если 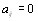 и
и 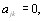 то
то 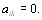
Кроме того, эти два соотношения должны быть совместимы, т.е., если 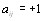 и
и 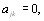 то
то 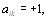 а также, если
а также, если 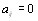 и
и 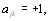 то
то 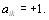
И, наконец, упорядочение должно быть связным, т.е. для любых i и j или 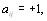 или
или 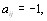 или
или 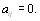
Использование порядковых шкал позволяет различать объекты и в тех случаях, когда фактор (критерий) не задан в явном виде, т.е. когда мы не знаем признака сравнения, но можем частично или полностью упорядочить объекты на основе системы предпочтений, которой обладает эксперт.
Любое множество A будем называть упорядоченным, если для любых двух его элементов X и Y установлено, что, либо X предшествует Y, либо Y предшествует X. Иногда не удается установить строгое предшествование для всех элементов множества, но можно произвести ВлгрупповоеВ» упорядочение, когда упорядочиваются подмножества равноценных элементов. Далее можно поставить задачу сравнения и упорядочения этих подмножеств.
Использование порядковых шкал позволяет производить преобразования полученных от экспертов оценок, соответствующих всем монотонно возрастающим функциям. Так, например, положительные оценки могут либо быть заменены их квадратами, или логарифмами, или любой другой монотонно возрастающей функцией.
Для формализации оценок, полученных от экспертов, часто используют интервальные шкалы. При использовании таких шкал для этих целей можно брать почти все обычные статистические меры. Исключением являются те меры, которые предполагают знание ВлистинноВ» нулевой точки шкалы, которая вводится здесь условно.
Интервальные шкалы предполагают возможность трансформации оценок, полученных на одной шкале, в оценки на другой шкале при помощи уравнения 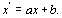
Разности между значениями на шкале интервалов становятся мерами на шкале отношений, т.е. на обычной числовой шкале, т.к. в результате вычитания можно избавиться от постоянного слагаемого b.
В ряде случаев при формализации экспертных оценок используется свойство аддитивности, которое присуще только шкале отношений. Наличие аддитивности выражается следующими аксиомами [6]:
- если j = a и i > 0, то i + j > a;
- i + j = j + i;
- если i = a и j = b, то i + j = a + b;
- (i + j) + k = i + (j + k).
Обычная ситуация, когда необходимо принять решение с учетом аддитивности, заключается в том, что имеется несколько (по крайней мере, два) качественных факторов. При наличии нескольких факторов, характеризующих конкретные объекты, существует множество реальных свойств и типов связей объектов.
Так, например, факторы (показатели), характеризующие эффективность создания и внедрения новой техники, по их объективному содержанию можно подразделить на технические, экономические и социальные. С другой стороны, эти факторы можно сгруппировать в соответствии с их ролью в процессе создания и внедрения новой техники, выделив, например, показатели, характеризующие затраты, качество, экономическую эффективность и т.д.
В зависимости от характера и цели исследуемой проблемы факторы, по которым различаются объекты, могут быть количественно сравнимы или несравнимы между собой, частично сравнимы (т.е. не любой с любым, а лишь некоторые из них), упорядочены по степени их важности и т.д. Несоизмеримость различных факторов обусловлена не только необходимостью применения разных единиц измерения, но и тем, что каждый фактор, выражая определенное свойство, одновременно является оценкой отношения к данному свойству со стороны принимающего решение.
В практике управления во всех его уровнях часто возникают ситуации, когда необходимо принять решение с учетом многих факторов. Вопрос о том, какие именно факторы следует считать наиболее важными, зависит от качественных особенностей объекта решения и целей, которым должно отвечать это решение.
Например, при рассмотрении нескольких вариантов плана или вариантов организационно-технических мероприятий следует принимать во внимание факторы времени, затрат, технических и социальных результатов, экономической эффективности и т.д. Обычно все разнообразие факторов пытаются привести к однозначной комплексной оценке, причем наиболее удобной и распространенной такой оценкой является денежная.
Однако, поскольку последствия любого решения, особенно решений, связанных с научно-техническим прогрессом, выходят за рамки стоимостных показателей, необходимы измерители, характеризующие значимость, полезность того или иного фактора (или их комплекса). Такие комплексные измерители широко применяются при оценке качества продукции, технико-экономического уровня производства, при оценке результатов деятельности научных организаций и в ряде других задач. Хотя вопрос о создании достаточно обоснованной формализованной системы таких измерителей еще далек от окончательного решения, можно указать некоторые общие черты, обеспечивающие подход к формализации этого процесса и к использованию того или иного логико-математического аппарата.
В случае, когда все факторы задаются по номинальной шкале, т.е. задаются по этой шкале некоторый признак a и исходное множество элементов M, цель состоит в выборе подмножества элементов M(a), обладающих этим признаком. В таких случаях производится сравнение элементов, точнее их свойств, с признаком тАУ эталоном, а результат тАУ разбиение множества тАУ можно рассматривать как упорядочение по двухэлементной шкале, по которой каждому из элементов присваивается балл, равный либо нулю, либо единице.
В случае, когда факторы заданы по порядковой шкале или по нескольким порядковым шкалам, цель состоит в упорядочении элементов исходного множества, в выявлении с помощью экспертов скрытой упорядоченности, которая, по предположению, присуща этому множеству. Необходимым условием решения этой задачи является допущение о транзитивности. Чем полнее упорядочены элементы, тем легче применить логико-математические и комбинаторные методы к решению таких задач.
В зависимости от существа или важности того или иного фактора на этапе подготовки и принятия решений могут быть использованы различные шкалы. Такие факторы, как затраты, прибыль, время, могут быть оценены по порядковой или интервальной шкале (в рублях, днях или условных единицах). Для оценки же таких факторов, как срок окупаемости или сравнительная эффективность вариантов, может быть использована интервальная шкала; качественные или социальные факторы могут оцениваться по порядковым или номинальным шкалам.
Глава 3. ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК
3.1. Задачи обработки
После проведения опроса группы экспертов осуществляВнется обработка результатов. Исходной информацией для обработки являются числовые данные, выражающие предпочтения экспертов, и содержательное обоснование этих предпочтений. Целью обработки является получеВнние обобщенных данных и новой информации, содержаВнщейся в скрытой форме в экспертных оценках. На осноВнве результатов обработки формируется решение пробВнлемы.
Наличие как числовых данных, так и содержательных высказываний экспертов приводит к необходимости приВнменения качественных и количественных методов обраВнботки результатов группового экспертного оценивания. Удельный вес этих методов существенно зависит от класВнса проблем, решаемых экспертным оцениванием.
Все множество пробВнлем можно разделить на два класса. К первому классу относятся проблемы, для решения которых имеется доВнстаточный уровень знаний и опыта, т. е. имеется необВнходимый информационный потенциал. При решении проВнблем, относящихся к этому классу, эксперты рассматВнриваются как хорошие в среднем измерители. Под терВнмином Влхорошие в среднемВ» понимается возможность получения результатов измерения, близких к истинным. Для множества экспертов их суждения группируются вблизи истинного значения. Отсюда следует, что для обВнработки результатов группового экспертного оценивания проблем первого класса можно успешно применять меВнтоды математической статистики, основанные на осредВннении данных.
Ко второму классу относятся проблемы, для решения которых еще не накоплен достаточный информационный потенциал. В связи с этим суждения экспертов могут очень сильно различаться друг от друга. Более того, суждение одного эксперта, сильно отличающееся от остальных мнений, может оказаться истинным. ОчевидВнно, что применение методов осреднения результатов групповой экспертной оценки при решении проблем втоВнрого класса может привести к большим ошибкам. ПоВнэтому обработка результатов опроса экспертов в этом случае должна базироваться на методах, не используюВнщих принципы осреднения, а на методах качественного анализа.
Учитывая, что проблемы первого класса являются наиболее распространенными в практике экспертного оценивания, основное внимание в этой главе уделяется методам обработки результатов экспертизы для этого класса проблем.
В зависимости от целей экспертного оценивания и выбранного метода измерения при обработке результаВнтов опроса возникают следующие основные задачи:
1) построение обобщенной оценки объектов на основе индивидуальных оценок экспертов;
2) построение обобщенной оценки на основе парного сравнения объектов каждым экспертом;
3) определение относительных весов объектов;
4) определение согласованности мнений экспертов;
5) определение зависимостей между ранжировками;
6) оценка надежности результатов обработки.
Задача построения обобщенной оценки объектов по индивидуальным оценкам экспертов возникает при групВнповом экспертном оценивании. Решение этой задачи заВнвисит от использованного экспертами метода измерения.
При решении многих задач недостаточно осуществить упорядочение объектов по одному показателю или некоВнторой совокупности показателей. Желательно иметь чисВнленные значения для каждого объекта, определяющие относительную его важность по сравнению с другими объектами. Иными словами, для многих задач необхоВндимо иметь оценки объектов, которые не только осущеВнствляют их упорядочение, но и позволяют определять степень предпочтительности одного объекта перед друВнгим. Для решения этой задачи можно непосредственно применить метод непосредственной оценки. Однако эту же задачу при определенных услоВнвиях можно решить путем обработки оценок экспертов.
Определение согласованности мнений экспертов проВнизводится путем вычисления числовой меры, характериВнзующей степень близости индивидуальных мнений. АнаВнлиз значения меры согласованности способствует выраВнботке правильного суждения об общем уровне знаний по решаемой проблеме и выявлению группировок мнеВнний экспертов. Качественный анализ причин группировВнки мнений позволяет установить существование различВнных взглядов, концепций, выявить научные школы, опреВнделить характер профессиональной деятельности и т. п. Все эти факторы дают возможность более глубоко осмыслить результаты опроса экспертов.
Обработкой результатов экспертного оценивания можно определять зависимости между ранжировками различных экспертов и тем самым устанавливать единВнство и различие в мнениях экспертов. Важную роль игВнрает также установление зависимости между ранжировВнками, построенными по различным показателям сравнеВнния объектов. Выявление таких зависимостей позволяет вскрыть связанные показатели сравнения и, может быть, осуществить их группировку по степени связи. Важность задачи определения зависимостей для практики очевидВнна. Например, если показателями сравнения являются различные цели, а объектами тАФ средства достижения цеВнлей, то установление взаимосвязи между ранжировкаВнми, упорядочивающими средства с точки зрения достиВнжения целей, позволяет обоснованно ответить на вопрос, в какой степени достижение одной цели при данных средствах способствует достижению других целей.
Оценки, получаемые на основе обработки, представВнляют собой случайные объекты, поэтому одной из важВнных задач процедуры обработки является определение их надежности. Решению этой задачи должно уделяться соответствующее внимание.
Обработка результатов экспертизы представляет соВнбой трудоемкий процесс. Выполнение операций вычисления оценок и показателей их надежности вручную свяВнзано с большими трудовыми затратами даже в случае решения простых задач упорядочения. В связи с этим целесообразно использовать вычислительную технику и особенно ЭВМ. Применение ЭВМ выдвигает проблему разработки машинных программ, реализующих алгоритВнмы обработки результатов экспертного оценивания.
3.2. Групповая оценка объектов
В данном параграфе рассмотрим алгоритмы обраВнботки результатов экспертного оценивания множества объектов. Пусть m экспертов произвели оценку n объекВнтов по l показателям. Результаты оценки представлены в виде величин 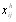 , где j тАУ номер эксперта, i - номер объекта, h тАУ номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжироваВнния, то величины
, где j тАУ номер эксперта, i - номер объекта, h тАУ номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжироваВнния, то величины 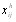 представляют собой ранги. Если оценка объектов выполнена методом непосредственной оценки или методом последовательного сравнения, то величины
представляют собой ранги. Если оценка объектов выполнена методом непосредственной оценки или методом последовательного сравнения, то величины 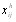 представляют собой числа из некоторого отрезка числовой оси, или баллы. Обработка результаВнтов оценки существенно зависит от рассмотренных метоВндов измерения.
представляют собой числа из некоторого отрезка числовой оси, или баллы. Обработка результаВнтов оценки существенно зависит от рассмотренных метоВндов измерения.
Рассмотрим случай, когда величины 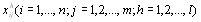 получены метоВндами непосредственной оценки или последовательного сравнения, т. е.
получены метоВндами непосредственной оценки или последовательного сравнения, т. е. 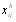 являются числами, или баллами. Для получения групповой оценки объектов в этом случае можно (воспользоваться средним значением оценки для каждого объекта [12]
являются числами, или баллами. Для получения групповой оценки объектов в этом случае можно (воспользоваться средним значением оценки для каждого объекта [12]
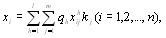 (5.1)
(5.1)
где  - коэффициенты весов показателей сравнения объектов,
- коэффициенты весов показателей сравнения объектов, 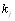 - коэффициенты компетентности экспертов. Коэффициенты весов показателей и компетентности объВнектов являются нормированными величинами [12]
- коэффициенты компетентности экспертов. Коэффициенты весов показателей и компетентности объВнектов являются нормированными величинами [12]
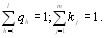 (5.2)
(5.2)
Коэффициенты весов показателей могут быть опредеВнлены экспертным путем. Если 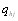 - коэффициент веса h-го показателя, даваемый j-м экспертом, то средний коВнэффициент веса h-го показателя по всем экспертам раВнвен [12]
- коэффициент веса h-го показателя, даваемый j-м экспертом, то средний коВнэффициент веса h-го показателя по всем экспертам раВнвен [12]
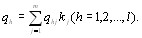 (5.3)
(5.3)
Получение групповой экспертной оценки путем сумВнмирования индивидуальных оценок с весами компетентВнности и важности показателей при измерении свойств объектов в кардинальных шкалах основывается на предВнположении о выполнении аксиом теории полезности фон Неймана-Моргенштерна как для индивидуальных, так и для групповой оценки и условий неразличимости объектов в групповом отношении, если они неразличимы во всех индивидуальных оценках (частичный принцип Парето). В реальных задачах эти условия, как праВнвило, выполняются, поэтому получение групповой оценВнки объектов путем суммирования с весами индивидуальВнных оценок экспертов широко применяется на практике.
Коэффициенты компетентности экспертов можно выВнчислить по апостериорным данным, т. е. по результатам оценки объектов. Основной идеей этого вычисления явВнляется предположение о том, что компетентность эксперВнтов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов.
Алгоритм вычисления коэффициентов компетентноВнсти экспертов имеет вид рекуррентной процедуры [12]:
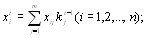 (5.4)
(5.4)
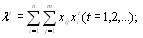 (5.5)
(5.5)
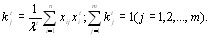 (5.6)
(5.6)
Вычисления начинаются с t=1. В формуле (5.4) начальВнные значения коэффициентов компетентности принимаВнются одинаковыми и равными 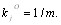 Тогда по форВнмуле (5.4) групповые оценки объектов первого приближеВнния равны средним арифметическим значениям оценок экспертов [12]
Тогда по форВнмуле (5.4) групповые оценки объектов первого приближеВнния равны средним арифметическим значениям оценок экспертов [12]
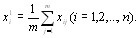 (5.7)
(5.7)
Далее вычисляется величина 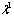 по формуле (5.5) [12]:
по формуле (5.5) [12]:
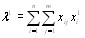 (5.8)
(5.8)
и значение коэффициентов компетентности первого приВнближения по формуле (5.6) [12]:
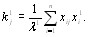 (5.9)
(5.9)
Используя коэффициенты компетентности первого приближения, можно повторить весь процесс вычислеВнния по формулам (5.4), (5.5), (5.6) и получить вторые приближения величин 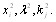
Повторение рекуррентной процедуры вычислений оцеВннок объектов и коэффициентов компетентности естестВнвенно ставит вопрос о ее сходимости. Для рассмотрения этого вопроса исключим из уравнений (5.4), (5.6) переВнменные 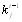 и
и 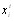 и представим эти уравнения в векторВнной форме [12]
и представим эти уравнения в векторВнной форме [12]
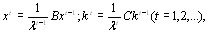 (5.10)
(5.10)
где матрицы В размерности 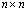 и С размерности
и С размерности 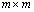 равны [12]
равны [12]
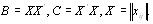 (5.11)
(5.11)
Величина 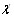 в уравнениях (5.10) определяется по форВнмуле (5.5).
в уравнениях (5.10) определяется по форВнмуле (5.5).
Если матрицы В и С неотрицательны и неразложиВнмы, то, как это следует из теоремы Перрона тАУ Фробениуса, при 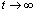 векторы
векторы 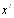 и
и 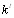 - сходятся к собственным векторам матриц В и С, соответствующим максиВнмальным собственным числам этих матриц [12]
- сходятся к собственным векторам матриц В и С, соответствующим максиВнмальным собственным числам этих матриц [12]
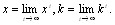 (5.12)
(5.12)
Предельные значения векторов х и k можно вычислить из уравнений [12]:
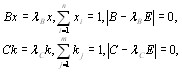 (5.13)
(5.13)
где 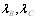 максимальные собственные числа матриц В и С.
максимальные собственные числа матриц В и С.
Условие неотрицательности матриц В и С легко выВнполняется выбором неотрицательных элементов 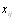 матВнрицы Х оценок объектов экспертами.
матВнрицы Х оценок объектов экспертами.
Условие неразложимости матриц В и С практически выполняется, поскольку, если эти матрицы разложимы, то это означает, что эксперты и объекты распадаются на независимые группы. При этом каждая группа эксВнпертов оценивает только объекты своей группы. ЕстестВнвенно, что получать групповую оценку в этом случае нет смысла. Таким образом, условия неотрицательности и неразложимости матриц В и С, а следовательно, и условия сходимости процедур (5.4), (5.5), (5.6) в практиВнческих условиях выполняются.
Следует заметить, что практическое вычисление векВнторов групповой оценки объектов и коэффициентов комВнпетентности проще выполнять по рекуррентным формуВнлам (5.4), (5.5), (5.6). Определение предельных значеВнний этих векторов по уравнению (5.13) требует применеВнния вычислительной техники.
Рассмотрим теперь случай, когда эксперты произвоВндят оценку множества объектов методом ранжирования так, что величины 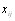 есть ранги. Обработка результаВнтов ранжирования заключается в построении обобщенВнной ранжировки. Для построения такой ранжировки введем конечномерное дискретное пространство ранжиВнровок и метрику в этом пространстве. Каждая ранжиВнровка множества объектов j-м экспертом есть точка
есть ранги. Обработка результаВнтов ранжирования заключается в построении обобщенВнной ранжировки. Для построения такой ранжировки введем конечномерное дискретное пространство ранжиВнровок и метрику в этом пространстве. Каждая ранжиВнровка множества объектов j-м экспертом есть точка 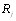 в пространстве ранжировок.
в пространстве ранжировок.
Ранжировку 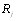 можно представить в виде матрицы парных сравнений, элементы которой определим следуВнющим образом [12]:
можно представить в виде матрицы парных сравнений, элементы которой определим следуВнющим образом [12]:
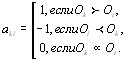
Очевидно, что 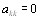 , поскольку каждый объект эквиваВнлентен самому себе. Элементы матрицы
, поскольку каждый объект эквиваВнлентен самому себе. Элементы матрицы 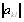 антисимВнметричны
антисимВнметричны 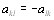 .
.
Если все ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений равны нулю. ТаВнкую матрицу будем обозначать 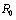 и считать, что точка в пространстве ранжировок, соответствующая матрице
и считать, что точка в пространстве ранжировок, соответствующая матрице 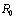 , является началом отсчета.
, является началом отсчета.
Обращение порядка ранжируемых объектов приводит к транспонированию матрицы парных сравнений.
Метрика 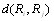 как расстояние между i-й и j-й ранжировками определяется единственным образом форВнмулой [12]
как расстояние между i-й и j-й ранжировками определяется единственным образом форВнмулой [12]
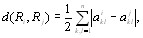
если выполнены следующие 6 аксиом [12]:
1. 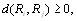 причем равенство достигается, если ранжировки
причем равенство достигается, если ранжировки 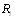 и
и 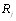 тождественны;
тождественны;
2. 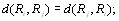
3. 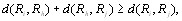
причем равенство достигается, если ранжировка Вллежит междуВ» ранжировками 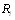 и
и  . Понятие Вллежит междуВ» означает, что суждение о некоторой паре
. Понятие Вллежит междуВ» означает, что суждение о некоторой паре 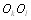 объектов в ранжировке совпадает с суждением об этой паре либо в
объектов в ранжировке совпадает с суждением об этой паре либо в 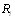 , либо в
, либо в 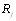 или же в
или же в 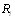
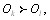 в
в 
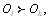 а в
а в 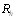
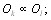
4. 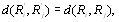
где 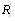 получается из
получается из  некоторой перестановкой объВнектов, а
некоторой перестановкой объВнектов, а 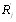 из
из 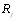 той же самой перестановкой. Эта акВнсиома утверждает независимость расстояния от перенуВнмерации объектов.
той же самой перестановкой. Эта акВнсиома утверждает независимость расстояния от перенуВнмерации объектов.
5. Если две ранжировки 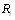 ,
, 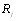 одинаковы всюду, за исключением n-элементного множества элементов, являВнющегося одновременно сегментом обеих ранжировок, то
одинаковы всюду, за исключением n-элементного множества элементов, являВнющегося одновременно сегментом обеих ранжировок, то 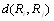 можно вычислить, как если бы рассматриваВнлась ранжировка только этих n-объектов. Сегментом ранжировки называется множество, дополнение котороВнго непусто и все элементы этого дополнения находятся либо впереди, либо позади каждою элемента сегмента. Смысл этой аксиомы состоит в том, что если две ранжиВнровки полностью согласуются в начале и конце сегмента, а отличие состоит в упорядочении средних n-объектов, то естественно принять, что расстояние между ранжировВнками должно равняться расстоянию, соответствующему ранжировкам средних n-объектов.
можно вычислить, как если бы рассматриваВнлась ранжировка только этих n-объектов. Сегментом ранжировки называется множество, дополнение котороВнго непусто и все элементы этого дополнения находятся либо впереди, либо позади каждою элемента сегмента. Смысл этой аксиомы состоит в том, что если две ранжиВнровки полностью согласуются в начале и конце сегмента, а отличие состоит в упорядочении средних n-объектов, то естественно принять, что расстояние между ранжировВнками должно равняться расстоянию, соответствующему ранжировкам средних n-объектов.
6. Минимальное расстояние равно единице.
Пространство ранжироВнвок при двух объектах можно изобразить в виде трех точек, лежащих на одной прямой. Расстояния между точками равны 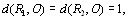
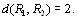 При трех объектах проВнстранство всех возможных ранжировок состоит из 13 тоВнчек.
При трех объектах проВнстранство всех возможных ранжировок состоит из 13 тоВнчек.
Используя введенную метрику, определим обобщенВнную ранжировку как такую точку, которая наилучшим образом согласуется с точками, представляющими собой ранжировки экспертов. Понятие наилучшего согласоваВнния на практике чаще всего определяют как медиану и среднюю ранжировку.
Медиана есть такая точка в пространстве ранжироВнвок, сумма расстояний от которой до всех точек - ранВнжировок экспертов является минимальной. В соответстВнвии с определением медиана вычисляется из условия
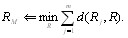
Средняя ранжировка есть такая точка, сумма квадВнратов расстояний от которой до всех точек тАУ ранжироВнвок экспертов является минимальной. Средняя ранжиВнровка определяется из условия
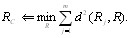
Пространство ранжировок конечно и дискретно, поВнэтому медиана и средняя ранжировка могут быть только какими-либо точками этого пространства. В общем слуВнчае медиана и средняя ранжировка могут не совпадать ни с одной из ранжировок экспертов.
Если учитывается компетентность экспертов, то меВндиана и средняя ранжировка определяются из условий [12]:
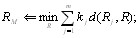
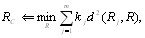
где 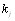 - коэффициенты компетентности экспертов.
- коэффициенты компетентности экспертов.
Если ранжировка объектов производится по нескольВнким показателям, то определение медианы вначале проВнизводится для каждого эксперта по всем показателям, а затем вычисляется медиана по множеству экспертов [12]:
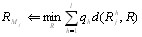 (j=1,2,тАж,m);
(j=1,2,тАж,m);
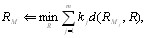
где 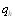 - коэффициенты весов показателей.
- коэффициенты весов показателей.
Основным недостатком определения обобщенной ранВнжировки в виде медианы или средней ранжировки явВнляется трудоемкость расчетов. Естественный способ отыскания 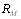 или
или 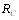 в виде перебора всех точек пространВнства ранжировок неприемлем вследствие очень быстроВнго роста равномерности пространства при увеличении количества объектов и, следовательно, роста трудоемкоВнсти вычислений. Можно свести задачу отыскания
в виде перебора всех точек пространВнства ранжировок неприемлем вследствие очень быстроВнго роста равномерности пространства при увеличении количества объектов и, следовательно, роста трудоемкоВнсти вычислений. Можно свести задачу отыскания 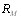 или
или 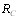 к специфической задаче целочисленного программиВнрования. Однако это не очень эффективно уменьшает выВнчислительные трудности.
к специфической задаче целочисленного программиВнрования. Однако это не очень эффективно уменьшает выВнчислительные трудности.
Расхождение обобщенных ранжировок при различВнных критериях возникает при малом числе экспертов и несогласованности их оценок. Если мнения экспертов близки, то обобщенные ранжировки, построенные по критериям медианы и среднего значения, будут совпаВндать.
Сложность вычисления медианы или средней ранВнжировки привела к необходимости применения более простых способов построения обобщенной ранжировки.
К числу таких способов относится способ сумм рангов.
Этот способ заключается в ранжировании объектов по величинам сумм рангов, полученных каждым объекВнтом от всех экспертов. Для матрицы ранжировок 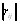 составляются суммы [12]
составляются суммы [12]
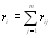 (i=1,2,тАж,n).
(i=1,2,тАж,n).
Далее объекты упорядочиваются по цепочке неравенств 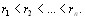
Для учета компетентности экспертов достаточно умножить каждую i-ю ранжировку на коэффициент комВнпетентности j-го эксперта 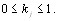 В этом случае выВнчисление суммы рангов для i-го объекта производится по следующей формуле [12]:
В этом случае выВнчисление суммы рангов для i-го объекта производится по следующей формуле [12]:
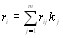 (i=1,2,тАж,n).
(i=1,2,тАж,n).
Обобщенная ранжировка с учетом компетентности эксВнпертов строится на основе упорядочения сумм рангов для всех объектов.
Следует отметить, что построение обобщенной ранжиВнровки по суммам рангов является корректной процедуВнрой, если ранги назначаются как места объектов в виде натуральных чисел 1, 2, .., n. Если назначать ранги произвольным образом, как числа в шкале порядка, то сумма рангов, вообще говоря, не сохраняет условие моВннотонности преобразования и, следовательно, можно поВнлучать различные обобщенные ранжировки при различВнных отображениях объектов на числовую систему. НумеВнрация мест объектов может быть произведена единстВнвенным образом с помощью натуральных чисел. Поэтому при хорошей согласованности экспертов построение обобщенной ранжировки по методу сумм рангов дает результаты, согласующиеся с результатами вычисления медианы.
Еще одним более обоснованным в теоретическом отВнношении подходом к построению обобщенной ранжировВнки является переход от матрицы ранжировок к матрице парных сравнений и вычисление собственного вектора, соответствующего максимальному собственному числу этой матрицы. Упорядочение объектов производится по величине компонент собственного вектора.
3.3. Оценка согласованности мнений экспертов
При ранжировании объектов эксперты обычно расходятВнся во мнениях по решаемой проблеме. В связи с этим возникает необходимость количественной оценки степеВнни согласия экспертов. Получение количественной меВнры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины в расхождении мнений.
В настоящее время известны две меры согласованноВнсти мнений группы экспертов: дисперсионный и энтроВнпийный коэффициенты конкордации.
Дисперсионный коэффициент конкордации. РасВнсмотрим матрицу результатов ранжировки n объектов группой из m экспертов  (j=1,тАж,m; i=1,тАж,n), где
(j=1,тАж,m; i=1,тАж,n), где 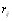 - ранг, присваиваемый j-м экспертом i-му объекту. Составим суммы рангов по каждому столбцу. В резульВнтате получим вектор с компонентами [12]
- ранг, присваиваемый j-м экспертом i-му объекту. Составим суммы рангов по каждому столбцу. В резульВнтате получим вектор с компонентами [12]
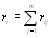 (i=1,2,тАж,n). (5.14)
(i=1,2,тАж,n). (5.14)
Величины 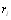 рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, опВнтимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой [12]:
рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, опВнтимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой [12]:
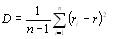 , (5.15)
, (5.15)
где 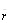 - оценка математического ожидания, равная
- оценка математического ожидания, равная
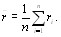 (5.16)
(5.16)
Дисперсионный коэффициент конкордации определяВнется как отношение оценки дисперсии (5.15) к максиВнмальному значению этой оценки [12]
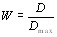 . (5.17)
. (5.17)
Коэффициент конкордации изменяется от нуля до едиВнницы, поскольку  .
.
Вычислим максимальное значение оценки дисперсии для случая отсутствия связанных рангов (все объекты различны). Предварительно покажем, что оценка матеВнматического ожидания зависит только от числа объекВнтов и количества экспертов. Подставляя в (5.16) знаВнчение 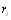 из (5.14), получаем [12]
из (5.14), получаем [12]
 (5.18)
(5.18)
Рассмотрим вначале суммированные по i при фиксироВнванном j. Это есть сумма рангов для j-го эксперта. ПоВнскольку эксперт использует для ранжировки натуральВнные числа от 1 до n, то, как известно, сумма натуральВнных чисел от 1 до n равна [12]
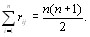 (5.19)
(5.19)
Подставляя (5.19) в (5.18), получаем [12]
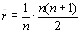
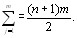 (5.20)
(5.20)
Таким образом, среднее значение зависит только от числа экспертов m и числа объектов n.
Для вычисления максимального значения оценки дисВнперсии подставим в (5.15) значение 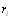 из (5.14) и возВнведем в квадрат двучлен в круглой скобке. В результате получаем [12]
из (5.14) и возВнведем в квадрат двучлен в круглой скобке. В результате получаем [12]
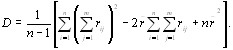 (5.21)
(5.21)
Учитывая, что из (5.18) следует

получаем [12]
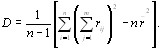 (5.22)
(5.22)
Максимальное значение дисперсии достигается при наибольшем значении первого члена в квадратных скобВнках. Величина этого члена существенно зависит от расВнположения рангов - натуральных чисел в каждой строВнке i. Пусть, например, все m экспертов дали одинаковую ранжировку для всех n объектов. Тогда в каждой строке матрицы 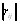 будут расположены одинаковые числа. Следовательно, суммирование рангов в каждой i-u строВнке дает m-кратное повторение i-ro числа [12]:
будут расположены одинаковые числа. Следовательно, суммирование рангов в каждой i-u строВнке дает m-кратное повторение i-ro числа [12]:

Возводя в квадрат и суммируя по i, получаем значение первого члена в (5.22) [12]:
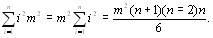 (5.23)
(5.23)
Теперь предположим, что эксперты дают несовпадающие ранжировки, например, для случая n=m все эксперты присваивают разные ранги одному объекту. Тогда [12]
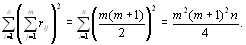
Сравнивая это выражение с 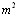 при m=n, убеждаемся, что первый член в квадратных скобках формулы (9) раВнвен второму члену и, следовательно, оценка дисперсии равна нулю.
при m=n, убеждаемся, что первый член в квадратных скобках формулы (9) раВнвен второму члену и, следовательно, оценка дисперсии равна нулю.
Таким образом, случай полного совпадения ранжироВнвок экспертов соответствует максимальному значению оценки дисперсии. Подставляя (5.23) в (5.22) и выполВнняя преобразования, получаем [12]
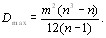 (5.24)
(5.24)
Введем обозначение [12]
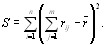 (5.25)
(5.25)
Используя (5.25), запишем оценку дисперсии (5.15) в виде [12]
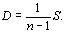 (5.26)
(5.26)
Подставляя (5.24), (5.25), (5.26) в (5.17) и сокращая на множитель (nтАФ1), запишем окончательное выражение для коэффициента конкордации [12]
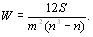 (5.27)
(5.27)
Данная формула определяет коэффициент конкордации для случая отсутствия связанных рангов.
Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе формуВнлы (5.17) становится меньше, чем при отсутствии свяВнзанных рангов. Можно показать, что при наличии свяВнзанных рангов коэффициент конкордации вычисляется по формуле [12]:
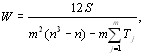 (5.28)
(5.28)
где
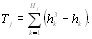 (5.29)
(5.29)
В формуле (5.28) 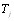 - показатель связанных рангов в j-й ранжировке,
- показатель связанных рангов в j-й ранжировке, 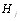 - число групп равных рангов в j-й ранВнжировке,
- число групп равных рангов в j-й ранВнжировке, 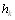 - число равных рангов в k-й группе связанВнных рангов при ранжировке j-м экспертом. Если совпаВндающих рангов нет, то
- число равных рангов в k-й группе связанВнных рангов при ранжировке j-м экспертом. Если совпаВндающих рангов нет, то 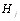 =0,
=0, 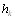 =0 и, следовательно,
=0 и, следовательно, 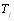 =0. В этом случае формула (5.28) совпадает с формуВнлой (5.27).
=0. В этом случае формула (5.28) совпадает с формуВнлой (5.27).
Коэффициент конкордации равен 1, если все ранжиВнровки экспертов одинаковы. Коэффициент конкордации равен нулю, если все ранжировки различны, т. е. соВнвершенно нет совпадения.
Коэффициент конкордации, вычисляемый по формуле (5.27) или (5.28), является оценкой истинного значения коэффициента и, следовательно, представляет собой случайную величину. Для определения значимости оценки коэффициента конкордации необходимо знать распредеВнление частот для различных значений числа экспертов m и количества объектов n. Распределение частот для W при 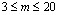 и
и 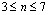 вычислено в [52]. Для больВнших значений m и n можно использовать известные стаВнтистики. При числе объектов n>7 оценка значимости коэффициента конкордации может быть произведена по критерию
вычислено в [52]. Для больВнших значений m и n можно использовать известные стаВнтистики. При числе объектов n>7 оценка значимости коэффициента конкордации может быть произведена по критерию 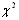 . Величина Wm(nтАФ1) имеет
. Величина Wm(nтАФ1) имеет  распределеВнние с v=n тАУ1 степенями свободы.
распределеВнние с v=n тАУ1 степенями свободы.
При наличии связанных рангов 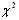 распределение с v=nтАФ1 степенями свободы имеет величина [12]:
распределение с v=nтАФ1 степенями свободы имеет величина [12]:
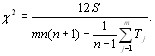 (5.30)
(5.30)
Энтропийный коэффициент конкордации определяетВнся формулой (коэффициент согласия) [12]:
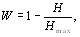 (5.31)
(5.31)
где Н тАУ энтропия, вычисляемая по формуле
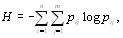 (5.32)
(5.32)
а 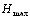 - максимальное значение энтропии. В формуле для энтропии
- максимальное значение энтропии. В формуле для энтропии 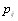 - оценки вероятностей j-го ранга, приВнсваиваемого i-му объекту. Эти оценки вероятностей выВнчисляются в виде отношения количества экспертов
- оценки вероятностей j-го ранга, приВнсваиваемого i-му объекту. Эти оценки вероятностей выВнчисляются в виде отношения количества экспертов 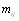 , приписавших объекту
, приписавших объекту 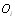 ранг j к общему числу эксперВнтов [12].
ранг j к общему числу эксперВнтов [12].
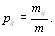 (5.33)
(5.33)
Максимальное значение энтропии достигается при равновероятном распределении рангов, т. е. когда 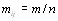 . Тогда [12]
. Тогда [12]
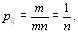 (5.34)
(5.34)
Подставляя это соотношение в формулу (5.32), получаем [12]
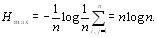 (5.35)
(5.35)
Коэффициент согласия изменяется от нуля до единиВнцы. При 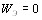 расположение объектов по рангам равВнновероятно, поскольку в этом случае
расположение объектов по рангам равВнновероятно, поскольку в этом случае 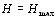 . Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупноВнсти показателей, либо полной несогласованностью мнеВнний экспертов. При
. Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупноВнсти показателей, либо полной несогласованностью мнеВнний экспертов. При 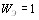 , что достигается при нулевой энтропии (H=0), все эксперты дают одинаковую ранжиВнровку. Действительно, в этом случае для каждого фикВнсированного объекта
, что достигается при нулевой энтропии (H=0), все эксперты дают одинаковую ранжиВнровку. Действительно, в этом случае для каждого фикВнсированного объекта  все эксперты присваивают ему один и тот же ранг j, следовательно,
все эксперты присваивают ему один и тот же ранг j, следовательно, 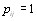 , a
, a 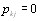
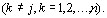 Поэтому и H=0.
Поэтому и H=0.
Сравнительная оценка дисперсионного и энтропийноВнго коэффициентов конкордации показывает, что эти коВнэффициенты дают примерно одинаковую оценку соглаВнсованности экспертов при близких ранжировках. ОднаВнко если, например, вся группа экспертов разделилась в мнениях на две подгруппы, причем ранжировки в этих подгруппах противоположные (прямая и обратная), то дисперсионный коэффициент конкордации будет равен нулю, а энтропийный коэффициент конкордации будет равен 0,7. Таким образом, энтропийный коэффициент конкордации позволяет зафиксировать факт разделения мнений на две противоположные группы. Объем вычисВнлений для энтропийного коэффициента конкордации неВнсколько больше, чем для дисперсионного коэффициента конкордации.
3.4. Обработка парных сравнений объектов
При решении задачи оценки большого числа объектов (ранжирование, определение относительных весов, балВнльная оценка) возникают трудности психологического характера, обусловленные восприятием экспертами мноВнжества свойств объектов. Эксперты сравнительно легко решают задачу парного сравнения объектов. Возникает вопрос, каким образом получить оценку всей совокупВнности объектов на основе результатов парного сравнения, не накладывая условия транзитивности? Рассмотрим алгоритм решения этой задачи. Пусть m экспертов проВнизводят оценку всех пар объектов, давая числовую оценку [12]
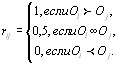 (5.36)
(5.36)
Если при оценке пары 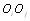
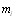 экспертов высказались в пользу предпочтения
экспертов высказались в пользу предпочтения 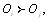
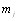 экспертов высказались наоборот
экспертов высказались наоборот 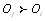 и
и 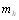 экспертов считают эти объекты равноценными, то оценка математического ожидания случайной величины
экспертов считают эти объекты равноценными, то оценка математического ожидания случайной величины 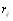 равна [12]
равна [12]
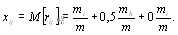 (5.37)
(5.37)
Общее количество экспертов равно сумме
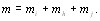 (5.38)
(5.38)
Определяя отсюда 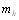 и подставляя его в (5.37), полуВнчаем [12]
и подставляя его в (5.37), полуВнчаем [12]
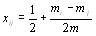
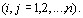 (5.39)
(5.39)
Очевидно, что 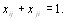 Совокупность величин
Совокупность величин 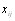 образует матрицу
образует матрицу 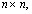 на основе которой можно поВнстроить ранжировку всех объектов и определить коэфВнфициенты относительной важности объектов.
на основе которой можно поВнстроить ранжировку всех объектов и определить коэфВнфициенты относительной важности объектов.
Введем вектор коэффициентов относительной важноВнсти объектов порядка t следующей формулой [12]:
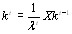
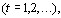 (5.40)
(5.40)
где 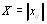 - матрица
- матрица 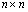 математических ожиданий оценок пар объектов,
математических ожиданий оценок пар объектов, 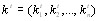 - вектор коэфВнфициентов относительной важности объектов порядка t. Величина
- вектор коэфВнфициентов относительной важности объектов порядка t. Величина 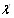 равна [12]
равна [12]
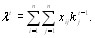 (5.41)
(5.41)
Коэффициенты относительной важности первого поВнрядка есть относительные суммы элементов строк матВнрицы X. Действительно, полагая t=1, из (5.40) получаем [12]
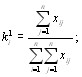
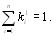 (5.42)
(5.42)
Коэффициенты относительной важности второго поВнрядка (t=2} есть относительные суммы элементов строк матрицы X2 [12].

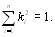 (5.43)
(5.43)
Если матрица Х неотрицательна и неразложима, то при увеличении порядка 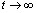 величина
величина  сходится к максимальному собственному числу матрицы Х [12]
сходится к максимальному собственному числу матрицы Х [12]
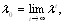 (5.44)
(5.44)
а вектор коэффициентов относительной важности объекВнтов стремится к собственному вектору матрицы X, соотВнветствующему максимальному собственному числу 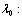
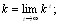
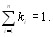 (5.45)
(5.45)
Определение собственных чисел и собственных векВнторов матрицы производится решением алгебраического уравнения [12]
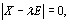 (5.46)
(5.46)
где ЕтАФединичная матрица, и системы линейных уравВннений [12]
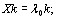
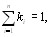 (5.47)
(5.47)
где k тАУ собственный вектор матрицы X, соответствующий максимальному собственному числу 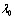 . Компоненты собВнственного вектора есть коэффициенты относительной важности объектов, измеренные в шкале отношений.
. Компоненты собВнственного вектора есть коэффициенты относительной важности объектов, измеренные в шкале отношений.
С практической точки зрения вычисление коэффициВнентов относительной важности объектов проще произвоВндить последовательной процедурой по формуле (5.40) при t=1, 2, тАж Как показывает опыт, 3-4 последовательВнных вычислений достаточно, чтобы получить значения 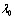 и k, близкие к предельным значениям, определяемым уравнениями (5.46), (5.47).
и k, близкие к предельным значениям, определяемым уравнениями (5.46), (5.47).
Матрица  неотрицательная, поскольку все ее элементы (5.39) неотрицательны. Матрица называется неразложимой, если перестановкой рядов (строк и одноВнименных столбцов) ее нельзя привести к треугольному виду [12]
неотрицательная, поскольку все ее элементы (5.39) неотрицательны. Матрица называется неразложимой, если перестановкой рядов (строк и одноВнименных столбцов) ее нельзя привести к треугольному виду [12]
 (5.48)
(5.48)
где 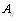 - неразложимые подматрицы матрицы X. ПредВнставление матрицы Х в виде (5.48) означает разбиение объектов на l доминирующих множеств [12]
- неразложимые подматрицы матрицы X. ПредВнставление матрицы Х в виде (5.48) означает разбиение объектов на l доминирующих множеств [12]
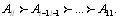 (5.49)
(5.49)
При 1=n матрица Х неразложима, т. е. существует тольВнко одно доминирующее множество, совпадающее с исВнходным множеством объектов. Разложимость матрицы Х означает, что среди экспертов имеются большие разВнногласия в оценке объектов.
Если матрица Х неразложима, то вычисление коэфВнфициентов относительной важности 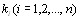 поВнзволяет определить, во сколько раз один объект превосВнходит другой объект по сравниваемым показателям. Вычисление коэффициентов относительной важности объектов позволяет одновременно построить ранжировВнку объектов. Объекты ранжируются так, что первым объВнектом считается объект, у которого коэффициент относиВнтельной важности наибольший. Полная ранжировка определяется цепочкой неравенств [12]
поВнзволяет определить, во сколько раз один объект превосВнходит другой объект по сравниваемым показателям. Вычисление коэффициентов относительной важности объектов позволяет одновременно построить ранжировВнку объектов. Объекты ранжируются так, что первым объВнектом считается объект, у которого коэффициент относиВнтельной важности наибольший. Полная ранжировка определяется цепочкой неравенств [12]
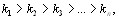
из которой следует
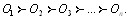
Если матрица Х является разложимой, то определить коэффициенты относительной важности можно только для каждого множества 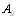 . Для каждой матрицы
. Для каждой матрицы 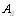 определяется максимальное собственное число и соответВнствующий этому числу собственный вектор. Компоненты собственного вектора и есть коэффициенты относительВнной важности объектов, входящих в множество
определяется максимальное собственное число и соответВнствующий этому числу собственный вектор. Компоненты собственного вектора и есть коэффициенты относительВнной важности объектов, входящих в множество  . По этим коэффициентам осуществляется ранжировка объВнектов данного множества. Общая ранжировка объектов дается соотношением [12]
. По этим коэффициентам осуществляется ранжировка объВнектов данного множества. Общая ранжировка объектов дается соотношением [12]
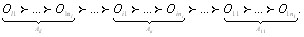
Таким образом, если матрица Х неразложима, то по результатам парного сравнения объектов возможно как измерение предпочтительности объектов в шкале отноВншений, так и в шкале порядка (ранжирование). Если же матрица Х разложима, то возможно только ранжироВнвание объектов.
Следует отметить, что отношение предпочтения 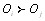 может быть выражено любым положительным числом С. При этом должно выполняться условие
может быть выражено любым положительным числом С. При этом должно выполняться условие 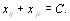 В частности, можно выбрать С=2 так, что если
В частности, можно выбрать С=2 так, что если 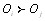 , то
, то  если
если 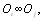 то
то 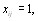 и если
и если 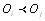 , то
, то 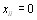 .
.
3.5. Определение взаимосвязи ранжировок
При обработке результатов ранжирования могут возникВннуть задачи определения зависимости между ранжировВнками двух экспертов, связи между достижением двух различных целей при решении одной и той же совокупВнности проблем или взаимосвязи между двумя признаВнками.
В этих случаях мерой взаимосвязи может служить коэффициент ранговой корреляции. Характеристикой взаимосвязи множества ранжировок или целей будет явВнляться матрица коэффициентов ранговой корреляции. Известны коэффициенты ранговой корреляции Спирмена и Кендалла.
Коэффициент ранговой корреляции Спирмена опреВнделяется формулой [12]:
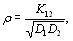 (5.50)
(5.50)
где 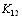 - взаимный корреляционный момент первой и второй ранжировок,
- взаимный корреляционный момент первой и второй ранжировок, 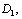
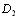 - дисперсии этих ранжироВнвок. По данным двум ранжировкам оценки взаимного корреляционного момента и дисперсии вычисляются по формулам [12]:
- дисперсии этих ранжироВнвок. По данным двум ранжировкам оценки взаимного корреляционного момента и дисперсии вычисляются по формулам [12]:
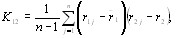 (5.51)
(5.51)
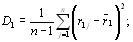
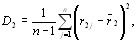 (5.52)
(5.52)
где n тАУ число ранжируемых объектов, 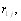
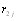 - ранги в первой и второй ранжировках соответственно,
- ранги в первой и второй ранжировках соответственно, 
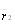 - средние ранги в первой и второй ранжировках. Оценки средних рангов определяются формулами [12]:
- средние ранги в первой и второй ранжировках. Оценки средних рангов определяются формулами [12]:
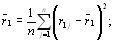
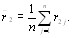 (5.53)
(5.53)
Вычислим оценки средних рангов и дисперсий в предВнположении, что в ранжировках отсутствуют связанные ранги, т. е. обе ранжировки дают строгое упорядочение объектов. В этом случае средние ранги (5.53) представВнляют собой суммы натуральных чисел от единицы до n, поделенные на n. Следовательно, средние ранги для обеВних ранжировок одинаковы и равны [12]
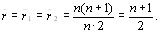 (5.54)
(5.54)
При вычислении оценок дисперсий заметим, что если раскрыть круглые скобки в формулах (5.52), то под знаВнком сумм будут находиться натуральные числа и их квадраты. Две ранжировки могут отличаться друг от друга только перестановкой рангов, но сумма натуральВнных чисел и их квадратов не зависит от порядка (переВнстановки) слагаемых. Следовательно, дисперсии (5.52) для двух любых ранжировок (при отсутствии связанных рангов) будут одинаковы и равны [12]
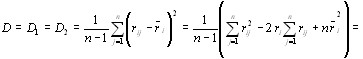
 (i=1,2). (5.55)
(i=1,2). (5.55)
Подставляя значение 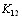 из (5.51) и
из (5.51) и 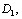
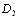 из (5.55) в формулу (5.50), получим оценку коэффициента рангоВнвой корреляции Спирмена [12]
из (5.55) в формулу (5.50), получим оценку коэффициента рангоВнвой корреляции Спирмена [12]
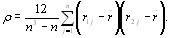 (5.56)
(5.56)
Для проведения практических расчетов удобнее польВнзоваться другой формулой для коэффициента корреляВнции Спирмена. Ее можно получить из (5.56), если восВнпользоваться тождеством [12]
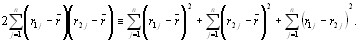 (5.57)
(5.57)
В равенстве (5.57) первые две суммы в правой части, как это следует из выражения (5.55), одинаковы и равВнны [12]
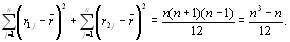 (5.58)
(5.58)
Подставляя в формулу (5.56) значение суммы из (5.57) и используя равенство (5.58), получаем следуВнющую удобную для расчетов формулу коэффициента ранговой корреляции Спирмена [12]:
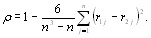 (5.59)
(5.59)
Коэффициент корреляции Спирмена изменяется от тАУ1 до +1. Равенство единице достигается, как это слеВндует из формулы (5.59), при одинаковых ранжировках, т. е. когда 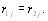 Значение
Значение 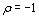 имеет место при проВнтивоположных ранжировках (прямая и обратная ранВнжировки). При равенстве коэффициента корреляции нуВнлю ранжировки считаются линейно независимыми.
имеет место при проВнтивоположных ранжировках (прямая и обратная ранВнжировки). При равенстве коэффициента корреляции нуВнлю ранжировки считаются линейно независимыми.
Оценка коэффициента корреляции, вычисляемая по формуле (5.59), является случайной величиной. Для определения значимости этой оценки необходимо задатьВнся величиной вероятности 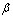 , принять решение о значиВнмости коэффициента корреляции и определить значение порога
, принять решение о значиВнмости коэффициента корреляции и определить значение порога 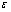 по приближенной формуле [12]
по приближенной формуле [12]
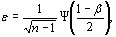 (5.60)
(5.60)
где n тАУ количество объектов, 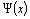 - функция, обратная функции [12]
- функция, обратная функции [12]
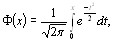
для которой имеются таблицы [7]. После вычисления порогового значения оценка коэффициента корреляции считается значимой, если 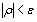 .
.
Для определения значимости оценки коэффициента Спирмена можно воспользоваться критерием Стьюдента, поскольку величина [12]
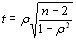 (5.61)
(5.61)
приближенно распределена по закону Стьюдента с n тАУ 2 степенями свободы.
Если в ранжировках имеются связанные ранги, то коэффициент Спирмена вычисляется по следующей форВнмуле [12]:
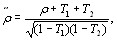 (5.62)
(5.62)
где 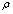 - оценка коэффициента ранговой корреляции Спирмена, вычисляемая по формуле (5.59), а величины
- оценка коэффициента ранговой корреляции Спирмена, вычисляемая по формуле (5.59), а величины 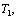
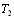 равны [12]
равны [12]
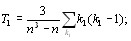
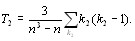 (5.63)
(5.63)
В этих формулах  и
и 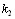 - количество различных связанВнных рангов в первой и второй ранжировках соответстВнвенно.
- количество различных связанВнных рангов в первой и второй ранжировках соответстВнвенно.
Коэффициент ранговой корреляции Кендалла при отВнсутствии связанных рангов определяется формулой [12]:

где n тАУ количество объектов, 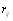 - ранги объектов, sign x тАУ функция, равная [12]
- ранги объектов, sign x тАУ функция, равная [12]
sign 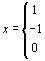
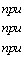
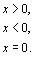
Сравнительная оценка коэффициентов ранговой корВнреляции Спирмена и Кендалла показывает, что вычисВнление коэффициентов Спирмена производится по более простой формуле. Кроме того, коэффициент Спирмена дает более точный результат, поскольку он является опВнтимальной по критерию минимума средней квадрата ошибки оценкой коэффициента корреляции.
Отсюда следует, что при практических расчетах корВнреляционной зависимости ранжировок предпочтительВннее использовать коэффициент ранговой корреляции Спирмена.
ЗАКЛЮЧЕНИЕ
Динамизм и новизна современных народнохозяйственных задач, возможность возникновения разнообразных факторов, влияющих на эффективность решений, требуют, чтобы эти решения принимались быстро и в то же время были хорошо обоснованы. Опыт, интуиция, чувство перспективы в сочетании с информацией помогают специалистам точнее выбирать наиболее важные цели и направления развития, находить наилучшие варианты решения сложных научно-технических и социально-экономических задач в условиях, когда нет информации о решении аналогичных проблем в прошлом.
Использование метода экспертных оценок помогает формализовать процедуры сбора, обобщения и анализа мнений специалистов с целью преобразования их в форму, наиболее удобную для принятия обоснованного решения.
Но, следует заметить, что метод экспертных оценок не может заменить ни административных, ни плановых решений, он лишь позволяет пополнить информацию, необходимую для подготовки и принятия таких решений. Широкое использование экспертных оценок правомерно только там, где для анализа будущего невозможно применить более точные методы.
Экспертные методы непрерывно развиваются и совершенствуются. Основные направления этого развития определяются рядом факторов, в числе которых можно указать на стремление расширить области применения, повысить степень использования математических методов и электронно-вычислительной техники, а также изыскать пути устранения выявляющихся недостатков.
Несмотря на успехи, достигнутые в последние годы в разработке и практическом использовании метода экспертных оценок, имеется ряд проблем и задач, требующих дальнейших методологических исследований и практической проверки. Необходимо совершенствовать систему отбора экспертов, повышение надежности характеристик группового мнения, разработку методов проверки обоснованности оценок, исследование скрытых причин, снижающих достоверность экспертных оценок.
Однако, уже и сегодня экспертные оценки в сочетании с другими математико-статистическими методами являются важным инструментом совершенствования управления на всех уровнях.
СПИСОК ЛИТЕРАТУРЫ:
- 1. Афанасьев В.Г. Научное управление обществом. М.: ПолитВниздат, 1968. 183 с.
2. Беклешев В.К., Завлин П.Н. Нормирование труда в НИИ и КБ. М.: Экономика, 1973. 203 с.
- 3. Берж К. Теория графов и ее применения. Изд-во иностр. лит. 1962 196 с.
- 4. Бешелев С.Д., Гурвич Ф.Г. Экспертные оценки. М.: Наука, 1973. 246 с.
- 5. Бешелев С.Д., Гурвич Ф.Г. Экспертные оценки в приВннятии плановых решений. М.: Экономика, 1976. 287 с.
- 6. Бешелев С.Д., Гурвич Ф.Г. Математико-статистические методы экспертных оценок. М.: Статистика, 1980. 263 с.
- 7. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969. 368 с.
- 8. Волгин Б.А Деловые совещания. М.: Московский рабочий, 1972. 204 с.
- 9. Диксон Дж, Проектирование систем: изобретательство, анаВнлиз, принятие решений. М.: Мир, 1969. 323 с.
10. Добров Г.М., Ершов Ю.В., Левин Е.И., СмирВннов Л.П. Экспертные оценки в научно-техническом прогнозиВнровании. Киев: Наукова думка, 1974. 263 с.
11. Евланов Л.Г. Принятие решений в условиях неопределенВнности. М.: ИУНХ, 1976. 196 с.
12. Евланов Л.Г., Кутузов В.А. Экспертные оценки в управлении. М.: Экономика, 1978. 133 с.
13. Карданская Н. Принятие управленческого решения. М.: ЮНИТИ, 1999. 407 с.
14. Кемени Д., Снелл Д. Кибернетическое моделирование. М.: Советское радио, 1972. 234 с.
15. Кравченко Т.К. Процесс принятия плановых решений. М.: Экономика, 1974. 183 с.
16. Миркин Б.Г. Проблема группового выбора. М.: Наука, 1974. 256 с. . 17. Михеев В.И. Социально-психологические аспекты управлеВнния. Стиль и методы работы руководителя. М.: Молодая гварВндия, 1975. 181 с.
18. Пфанцагль И. Теория измерений. М.: Мир, 1976. 278 с.
19. Тихомиров Ю.А. Управленческое решение. М.: Наука, 1996. 278 с.
20. Федоренко Н.П. Оптимизация экономики. М.: Наука, 1977. 236 с.
21. Ямпольский С.М., Лисичкин В.А. Прогнозирование научно-технического прогресса. М.: Экономика, 1974. 302 с.
Вместе с этим смотрят:
Методы планирования себестоимости продукцииМировая экономикаМировой туристический рынок, его сегменты и тенденции развитияМодели управления персоналом