Исследование элементарных функций
Красноярский Государственный Педагогический Университет им. В.П. Астафьева.
Реферат
На тему: ВлИсследование элементарных функцийВ».
Выполнила: Квашенко Д.В.
Проверил: Адольф В.А.
г. Красноярск
2005г.
Содержание:
- Определение элементарных функцийтАжтАжтАжтАжтАж.3
- Функция и её свойстватАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.3
- Способы задания функциитАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.4
- Определение функциитАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.4
- Исследование элементарных функцийтАжтАжтАж..6
а) Линейная функциятАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж....7
б) Степенная функциятАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.8
в) Показательная функциятАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж9
г) Логарифмическая функциятАжтАжтАжтАжтАжтАжтАжтАж.10
д) Тригонометрическая функциятАжтАжтАжтАжтАжтАж.11
- Y=sin xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж11
- Y=cos xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж13
- Y=tg xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.14
- Y=ctg xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж15
е) Обратно тригонометрическая функция.16
- Y=arcsin xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.16
- Y=arccos xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж17
- Y=arctg xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.18
- Y=arcctg xтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.19
- Список литературытАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.20
Определение элементарных функций.
Функции С (постоянная), xтБї, ах, 1оgа х, sin х, соs х, tg х, ctg x, аrcsin х, аrccos х, аrctg х называются простейшими элементарными функциями.
Применяя к этим функциям арифметические действия или операции функции от функции, мы будем получать новые более сложные фунВнкции, которые называются элементарными функциями.
Например, у = sin (xтБї) тАФ элементарная функВнция.
Элементарные функции нам известны из школьной математики.
Функция, и её свойства:
Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.
тЧППеременная х - независимая переменная или аргумент.
тЧППеременная у - зависимая переменная.
тЧПЗначение функции - значение у, соответствующее заданному
значению х.
тЧПОбласть определения функции - все значения, которые принимает независимая переменная.
тЧПОбласть значений функции (множество значений)- все значения, которые принимает функция.
тЧПФункция является четной - если для любого х из области определения функции выполняется равенство f(x)=f(-x).
тЧПФункция является нечетной - если для любого х из области определения функции выполняется равенство f(-x)=-f(x).
тЧПВозрастающая функция - если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2).
тЧПУбывающая функция - если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2).
Способы задания функции:
тЧПЧтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x) - заданная функция с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
тЧПНа практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.
Определение функции.
Функция, прежде всего, тАУ это одно из основных понятий математического анализа, и чтобы далее рассматривать различные функции, следует дать определение функции.
Пусть даны две переменные x и y с областями изменения X и Y. Предположим, что переменной x может быть приписано произвольное значение из области X без каких-либо ограничений. Тогда переменная y называется функцией от переменной x в области её изменения X, если по некоторому правилу или закону каждому значению x из X ставится в соответствие одно определенное значение y из Y.
Независимая переменная x называется также аргументом функции.В этом определении существенны два момента: во-первых, указание области X изменения аргумента x (её называют также областью определения функции) и, во-вторых, установление правила или закона соответствия между значениями x и y (Область Y изменения функции обычно не указывается, поскольку самый закон соответствия уже определяет множество принимаемых функцией значений).
Можно в определении понятия функции стать на более общую точку зрения, допуская, чтобы каждому значению x из X отвечало не одно, а несколько значений y (и даже бесконечное множество их). В подобных случаях функцию называют многозначной, в отличие от однозначной функции, определенной выше.
Для указания того факта, что y есть функция от x, пишут:y=f (x), y=g (x), y=F (x) и т.п.
Буквы f, g, F, тАж характеризуют именно то правило, по которому получается значение x, отвечающее заданному y. Поэтому, если одновременно рассматриваются различные функции от одного и того же аргумента x, связанные с различными законами соответствия, их не следует обозначать одной и той же буквой.
Хотя именно буква f связана со словом тАЬфункциятАЭ, но для обозначения функциональной зависимости может применяться и любая другая буква; иногда даже повторяют одну и ту же букву y: y=y(x). В некоторых случаях пишут аргумент и в виде значка при функции, например, ![]() .
.
Если, рассматривая функцию y=f(x), мы хотим отметить её частное значение, которое отвечает выбранному частному значению x, равному ![]() , то для обозначения его употребляют символ f(
, то для обозначения его употребляют символ f(![]() ). Например, если
). Например, если
F (x)=![]() , g (t)=
, g (t)=![]() , то f(1) означает численное значение функции f(x) при x=1, т.е. попросту число
, то f(1) означает численное значение функции f(x) при x=1, т.е. попросту число ![]() , аналогично, g(5) означает число 2, и т. д.
, аналогично, g(5) означает число 2, и т. д.
Теперь обратимся к самому правилу, или закону соответствия между значениями переменных, которое составляет сущность понятия функциональной зависимости.
Наиболее просто осуществление этого правила с помощью формулы, которая представляет функцию в виде аналитического выражения, указывающего те аналитические операции или действия над постоянными числами и над значением x, которые надо произвести, чтобы получить соответствующее значение y. Этот аналитический способ задания функции является наиболее важным для математического анализа.
Однако будет ошибочным думать, что это тАУ единственный способ, которым может быть задана функция. В самой математике нередки случаи, когда функция определяется без помощи формулы. Такова, например, функция E(x) тАУ тАЬцелая часть числа xтАЭ. Например,
E (1)=1, E (2,5)=2, E (хотя никакой формулы, выражающей E(x), у нас нет.
Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию обозначают C (f (x) = C).
Функция f (x) называется возрастающей (убывающей) на множестве X, если для любой пары чисел ![]() и
и ![]() этого множества из неравенства
этого множества из неравенства ![]() <
< ![]() следует, что f (
следует, что f (![]() ) < f (
) < f (![]() ) (f (
) (f (![]() ) > f (
) > f (![]() )).
)).
Функция f(x) называется четной, если область её определения X есть множество, симметричное относительно начала координат, и при любом x из X имеет место равенство f(-x)=f(x).
График четной функции симметричен относительно оси Oy.Функция f(x) называется нечетной, если область её определения X есть множество, симметричное относительно начала координат, и если при любом x из X имеет место равенство f(-x)=-f(x).
График нечетной функции симметричен относительно начала координат.
Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).
Действительно, пусть y(x)=f(x) + g(x). Тогда, если f(x) и g(x) тАУ четные, то y (-x) = f(-x) + g(-x) = f (x) + g (x) = y (x). Если же f (x) и g (x) тАУ нечетные функции, то функция y (x) также будет нечетной, y (-x) = f (-x) + g (-x) = -f (x) тАУ g (x) = -[f (x) + g (x)] = -y (x). (Для разности доказательство аналогичное).
Произведение двух четных или двух нечетных функций есть функция четная, а произведение четной функции на нечетную тАУ нечетная функция.
В самом деле, пусть y (x) = f (x)*g (x) и f (x) и g (x) тАУ четные функции, тогда y (-x) = f (-x)*g (-x) = f (x)*g (x) = y (x); если f (x) и g (x) тАУ нечетные функции, то y (-x) = f (-x)*g(-x) = [-f (x)]*[-g(x)] = y (x); если же f (x) тАУ четная, а g (x) тАУ нечетная функции, то y (x) = f (x)*g (-x) = f (x)*[-g (x)] = -y (x).
Функция f (x) называется периодической, если существует число Т ![]() 0 такое, что для любого значения x из области определения функции выполняется равенство f (x - T) = f (x) = f (x + T). Число T называется периодом функции. Если T тАУ период функции, то её периодом является также число тАУ T, так как f (x-T) = f [(x - T) +T] = f (x).
0 такое, что для любого значения x из области определения функции выполняется равенство f (x - T) = f (x) = f (x + T). Число T называется периодом функции. Если T тАУ период функции, то её периодом является также число тАУ T, так как f (x-T) = f [(x - T) +T] = f (x).
Если T тАУ период функции, то её периодом будет также и число kT, где k тАУ любое целое число (k=![]() 1,
1, ![]() 2,
2, ![]() 3; тАж). Действительно, f (x
3; тАж). Действительно, f (x ![]() 2T) = f [(x
2T) = f [(x![]() T)
T)![]() T] = f (x
T] = f (x![]() T) = f (x), f (x
T) = f (x), f (x ![]() 3T) = f [(x
3T) = f [(x ![]() 2T)
2T) ![]() T] = f (x
T] = f (x ![]() 2T) = f (x
2T) = f (x ![]() 2T) = f (x);обычно под периодом функции понимают наименьший из положительных периодов, если такой период существует.
2T) = f (x);обычно под периодом функции понимают наименьший из положительных периодов, если такой период существует.
Исследование элементарных функций .
Основные простейшие элементарные функции:
- Линейная функция y=kx+b;
- Степенная функция y=xтБї;
- Квадратичная функция;
- Показательная функция
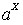 (0 <a
(0 <a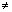 1);
1); - Логарифмическая функция
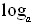 x (0 < a
x (0 < a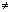 1);
1); - Тригонометрические функции: sin x, cos x, tg x, ctg x;
- Обратные тригонометрические функции: arcsin x, arccos x, arctg x, arcctg x.
y = kx + b
1. Областью определения линейной функции служит множество R всех действительных чисел, так как выражение kx+b имеет смысл при любых значениях x
2. Множеством значений линейной функции при k≠0 является множество R всех действительных чисел
3. Функция не является ни четной, ни нечетной, так как f (-x) = -kx + b .
4. Функция не является периодической, за исключением частного случая, когда функция имеет вид y=b.
5. Асимптоты графика функции не существуют.
6. Функция возрастает при k>0, функция убывает при k<0.
7. Функция не является ограниченной.
8. График линейной функции y=kx+b тАУ прямая линия. Для построения этого графика, очевидно, достаточно двух точек, например A(0; b) и B(-b/k; 0), если k≠0. График линейной функции y=kx+b может быть также построен с помощью параллельного переноса графика функции y=kx. Коэффициент k характеризует угол, который образует прямая y=kx и положительное направление оси Ox, поэтому k называется угловым коэффициентом. Если k>0, то этот угол острый, если k<0 тАУ тупой; а при k=0 прямая параллельна оси Ox.
9. Точек перегиба не существует.
10. Не существует экстремальных точек.
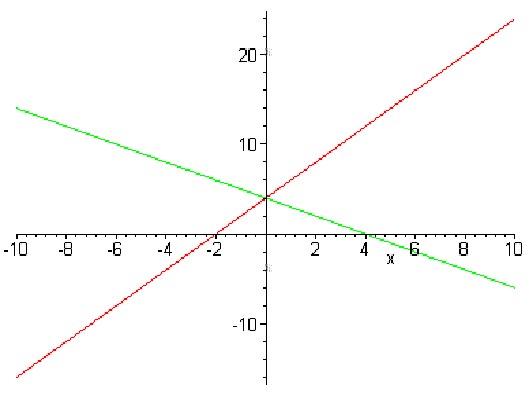
y=kx+b (k<0) y=kx+b (k>0)
Степенная функция.Степенная функция с натуральным показателем y=xn,
где n-натуральное число.
1. Область определения функции: D(f)= R;
2. Область значений: E(f)= (0;+тИЮ);
3. Функция является четной, т.е. f(-x)=f(x);
4. Нули функции: y=0 при x=0;
5. Функция убывает при x![]() (-тИЮ;0];
(-тИЮ;0];
6. Функция возрастает при x![]() [0;+ тИЮ);
[0;+ тИЮ);
- a) нет вертикальных асимптот
b) нет наклонных асимптот
8. Если n-четное, то экстремум функции x=0
Если n-нечетное, то экстремумов функции нет
9. Если n-четное, то точек перегиба нет
Если n-нечетное, то точка перегиба x=0
10. График функции:
a) Если n=2, то графиком функции является квадратная парабола;
b)Если п = 3, то функция задана форВнмулой у = х3. Ее граВнфиком является кубиВнческая тАВ парабола;
c)Если п тАФ нечетное натуральное число,тАГпричем п![]() 1, то функция обладает тАГтАГтАГсвойствами теми же, что и у = х3.
1, то функция обладает тАГтАГтАГсвойствами теми же, что и у = х3.
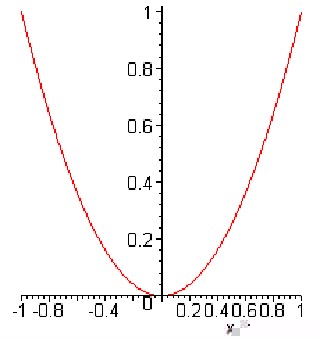
[2] 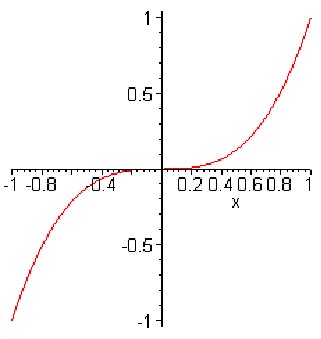
Рассмотрим свойства степенной функции с нечетным показателем (п![]() 1):
1):
1.тАВ Область определения функции: D(f)= R;
2. тАВОбласть значений [0,+тИЮ];
3. тАВФункция является четной, т.е. f(-х)=f(х);
4. тАВНули функции:тАВу = 0 при х = 0;
5. тАВФункция убывает на промежутке (-тИЮ;0), возрастает на промежутке (0;+тИЮ).
6. тАВГрафик функции:тАВ[1]
Рассмотрим свойства степенной функции с четным показателем :
1.тАВ Область определения функции: D(f)= R;
2. тАВОбласть значений: E(f)= R;
3. тАВФункция является нечетной, т.е. f(-х)=-f(х);
4. тАВНули функции:тАВу = 0 при х = 0;
5. тАВФункция возрастает на всей области определеВнния.
6. тАВГрафик функции:тАВ[2]
Показательная функция.Y = ax
- Область определения функции: -тИЮ < х < +тИЮ
- Множество значений функции: 0 < y < +тИЮ
- Функция ни четная, ни не чётная, так как f(-x) = a-x
- Функция не является периодической.
- Асимптоты графика функции:
Вертикальных асимптот не существует,
Горизонтальная асимптота у = 0
- Если а > 1, то функция возрастает на промежутке -тИЮ < x < +тИЮ (на рис.1);
- если 0 < a < 1, то функция убывает на промежутке -тИЮ < x < +тИЮ (на рис. 2);
- Точка (0; 1) тАУ единственная точка пересечения с осями координат.
9. Не существует точек перегиба.
10. Не существует экстремальных точек.
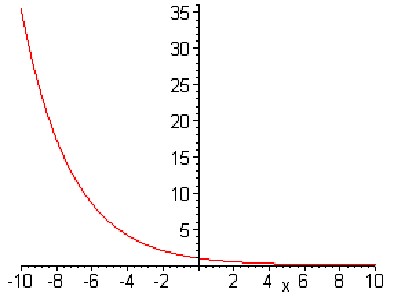
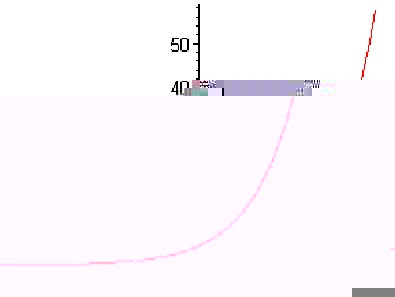
[2]
[1]
Логарифмическая функция.
Y = logax
- Область определения функции: 0 < x < тИЮ
- Множество значений функции: -тИЮ < y < +тИЮ
- Функция ни четная, ни нечетная, так как f(-x) = loga(-x)
- Функция не периодическая
- Асимптоты графика функции:
Горизонтальных асимптот не существует
- Если a > 1, то функция возрастает на промежутке 0 < x < +тИЮ (на рис.1);
если 0 < a < 1, то функция убывает на этом же промежутке (на рис.2);
- Точка (1; 0) тАУ единственная точка пересечения с осями
координат.
8.Не существует точек перегиба.
9.Не существует экстремальных точек.
[2]
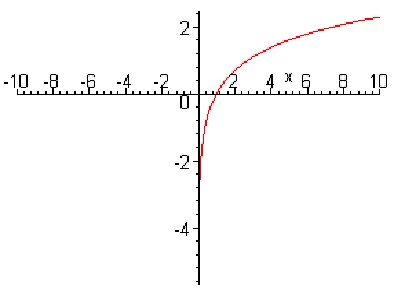

[1]
Тригонометрические функции.
Функция y=sin x
Свойства функции y=sin x:
- Область определения функции: D(f)=R;
- Область значений: E(f)=[-1;1];
- Функция является нечетной, т.е. sin(-x) = - sin x;
- Функция периодическая с положительным наименьшим периодом 2ПА;
- Нули функции: sin x = 0 при x = ПАk, k
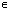 Z;
Z; - Функция принимает положительные значения: sin x>0 при x
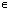 ( 2ПАk;тАВПА+2ПАk), k
( 2ПАk;тАВПА+2ПАk), k Z;
Z; - Функция принимает отрицательные значения: sin x<0 при x
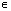 ( ПА+2ПАk;тАВ2ПА+2ПАk), k
( ПА+2ПАk;тАВ2ПА+2ПАk), k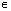 Z;
Z; - Функция возрастает на [-1;1] при x
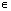 [ -
[ - +2ПАk;тАВ
+2ПАk;тАВ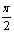 +2ПАk], k
+2ПАk], k Z;
Z; - Функция убывает на [1;-1] при x
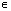 [
[ +2ПАk;тАВ
+2ПАk;тАВ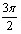 +2ПАk], k
+2ПАk], k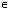 Z;
Z;
- Функция принимает наибольшее значение, равное 1, в точках x=
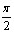 +2ПАk, k
+2ПАk, k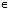 Z;
Z; - Функция принимает наименьшее значение, равное -1, в точках x=
 +2ПАk, k
+2ПАk, k Z;
Z; - a) нет вертикальных асимптот
b) нет горизонтальных асимптот
13. Графиком функции является синусоида.
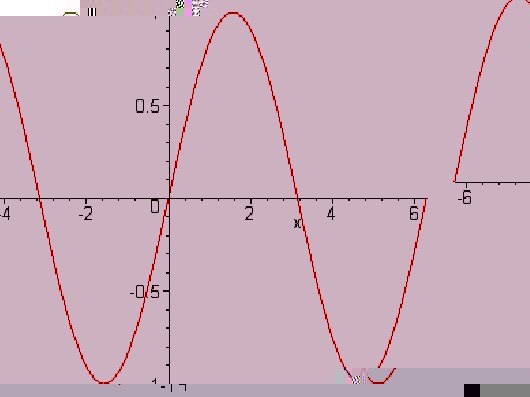
Функция y=cos x
Свойства функции y=cos x:
- Область определения функции: D(f)=R;
- Область значений: E(f)=[-1;1];
- Функция является четной, т.е. cos (-x) = cos x;
- Функция периодическая с наименьшим положительным периодом 2ПА;
- Нули функции: cos x = 0 при x =
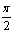 +ПАk, k
+ПАk, k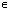 Z;
Z; - Функция принимает положительные значения: cos x>0 при x
 ( -
( -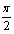 +2ПАk;
+2ПАk; 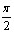 +2ПАk), k
+2ПАk), k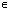 Z;
Z; - Функция принимает отрицательные значения: cos x<0 при x
 (
( 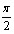 +2ПАk;тАВ
+2ПАk;тАВ +2ПАk), k
+2ПАk), k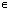 Z;
Z; - Функция возрастает на [-1;1] при x
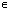 [ -ПА+2ПАk;тАВ2ПАk], k
[ -ПА+2ПАk;тАВ2ПАk], k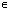 Z;
Z; - Функция убывает на [1;-1] при x
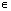 [2ПАk;тАВПА+2ПАk], k
[2ПАk;тАВПА+2ПАk], k Z;
Z; - Функция принимает наибольшее значение, равное 1, в точках x=2ПАk, k
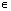 Z;
Z; - Функция принимает наименьшее значение, равное -1, в точках x=ПА+2ПАk, k
 Z;
Z; - a) нет вертикальных асимптот
b) нет горизонтальных асимптот
- Графиком функции является косинусоида:

Функция y=tg x
Свойства функции y=tg x:
- Область определения функции: D(f)=R , кроме чисел вида x =
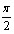 +ПАk, k
+ПАk, k Z;
Z; - Область значений: E(f)=R;
- Функция является нечетной, т.е. tg (-x) = - tg x;
- Функция периодическая с наименьшим положительным периодом ПА;
- Нули функции: tg x = 0 при x = ПАk, k
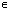 Z;
Z; - Функция принимает положительные значения: tg x>0 при x
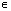 ( ПАk;
( ПАk; 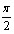 +ПАk), k
+ПАk), k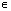 Z;
Z; - Функция принимает отрицательные значения: tg x<0 при x
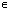 ( -
( - +ПАk;тАВПАk), k
+ПАk;тАВПАk), k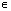 Z;
Z; - Функция возрастает на (-
 ;+тИЮ) при x
;+тИЮ) при x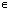 (-
(-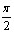 +ПАk ;тАВ
+ПАk ;тАВ +ПАk ), k
+ПАk ), k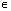 Z;
Z; - a) вертикальные асимптоты x=
 + ПАn
+ ПАn
b) наклонных асимптот нет
- Графиком функции является тангенсоида:
Функция y=ctg x
Свойства функции y=ctg x:
- Область определения функции: D(f)=R , кроме чисел вида x = ПАn , где n
 Z;
Z; - Область значений: E(f)=R;
- Функция является нечетной, т.е. ctg (-x) = - ctg x;
- Функция периодическая с наименьшим положительным периодом ПА;
- Нули функции: ctg x = 0 при x =
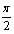 +ПАn, n
+ПАn, n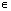 Z;
Z; - Функция принимает положительные значения: ctg x>0 при x
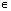 ( ПАn;
( ПАn; 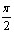 +ПАn), n
+ПАn), n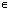 Z;
Z; - Функция принимает отрицательные значения: ctg x<0 при x
 (
( 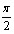 +ПАn;тАВПА +ПАn), n
+ПАn;тАВПА +ПАn), n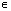 Z;
Z; - Функция убывает в каждом из промежутков (ПАn ;тАВПА +ПАn), n
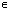 Z;
Z; - a) вертикальные асимптоты x= ПАn и x=0
![]()
![]()
b) наклонных асимптот нет
![]()
- Графиком функции является котангенсоида: y= ctgx
Обратно тригонометрические функции.
Функция y=arcsin x
Свойства функции y=arcsin x:
- Область определения функции: D(f)=[-1;1];
- Область значений: E(f)=[-
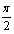 ;
; 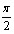 ];
]; - Функция является нечетной, т.е. arcsin (-x) = - arcsin x;
- Нули функции: arcsin x = 0 при x = 0;
- Функция возрастает на [-1;1];
- Функция принимает наибольшее значение
 при x=1;
при x=1; - Функция принимает наименьшее значение
 при x= -1;
при x= -1; - a) вертикальных асимптот нет
b) наклонных асимптот нет
- График функции y = arcsin x:

Функция y=arccos x
Свойства функции y=arccos x:
- Область определения функции: D(f)=(-1;1);
- Область значений: E(f)=[0; ПА];
- Функция не является ни четной, ни нечетной;
- Нули функции: arccos x = 0 при x = 1;
- Функция убывает на (-1;1);
- Функция принимает наибольшее значение ПА при x =-1;
- Функция принимает наименьшее значение 0 при x= 1;
- a) вертикальные асимптоты x=-1 и x=1
b)наклонных асимптот нет
- График функции y = arccos x:
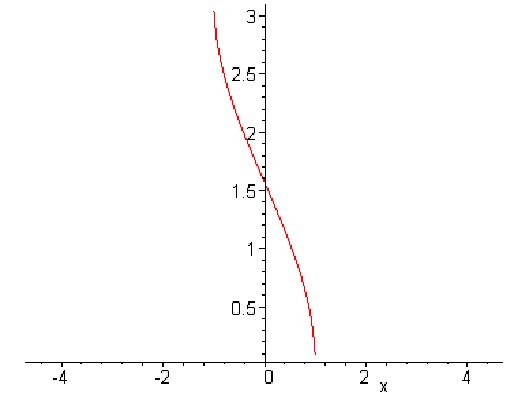
Функция y=arctg x
Свойства функции y=arctg x:
- Область определения функции: D(f)=R;
- Область значений: E(f)= (-
 ;
;  );
); - Функция является нечетной, т.е. arctg (- x) = - arctg x;
- Нули функции: arctg x = 0 при x = 0;
- Функция возрастает на R;
- a) нет вертикальных асимптот
- наклонные асимптоты y=
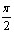 + ПАn
+ ПАn
- График функции y = arctg x:

Функция y=arcctg x
Свойства функции y=arcctg x:
- Область определения функции: D(f)=R;
- Область значений: E(f)= (0; ПА );
- Функция не является ни четной, ни нечетной;
- Нули функции: arctg x = 0 при x =
 ;
; - a) нет вертикальных асимптот
b) наклонные асимптоты y= ПАn
6.Функция убывает на R;
7.График функции y = arcctg x:
Литература:
- Э.С. Маркович ВлКурс высшей математикиВ»
- А.Г. Цыпкин ВлСправочник по математикеВ»
- М.М. Потапов, В.В. Александров, П.И. Пасиченко ВлАлгебра и анализ элементарных функцийВ»
Вместе с этим смотрят:
Исторические сведения о развитии тригонометрииИсторические сведения о тригонометрии
История математики
История открытия комплексных чисел