Вынужденное явление Рамана

Рассеяние Рамана1 в стоксову сторону.

Пусть пучок света падает на прозрачную среду, не содержаВнщую никаких включений посторонних тел и тщательно очищенную. Даже при максимально возможной частоте свет пучка рассеивается во все стороны, хотя и очень слабо. Рассеяние имеет место как в газообразных, так и в жидких и твердых телах. В газах рассеяние происВнходит, главным образом, на атомах и молекулах, в жидВнкостях и кристаллахтАФна флуктуациях и неоднородностях среды. В рассеянном свете имеются волны тех же длин, что и в падающем, но разной интенсивности в заВнвисимости от длины волны. Это рассеяние называется релеевским по имени Релея. Помимо рассеяния света с той же длиной волны наблюдается еще слабое свечеВнние с длиной волны, большей, чем падающая,тАФрамановское рассеяние. Механизм этого явления можно объВняснить на основе как квантовой теории, так, и классичеВнской волновой. Особенно просто выглядит квантовое описание этого явления.

Пусть квант излучения или, иначе, (поскольку , a ) рассеивается на молекуле, нахоВндящейся в основном состоянии с энергией возбуждая ее до одного из возможных для нее типов колеВнбаний с резонансной частотой . В результате рассеянный квант будет иметь меньшую энергию . Баланс энергии

(1)

позволяет рассчитать колебательные уровни молеВнкулы. Рассеянный свет имеет частоту , меньВншую частоты падающего света . Следовательно, рамановские линии являются стоксовыми. Рассеяние на уже возбужденной молекуле маловероятно, потому что линии с большей частотой , т. е. антистоксовые, имеют столь малую интенсивность, что обычно незаметны. ИнВнтенсивность рамановских линий рассчитывают на основе вероятности соответствующих переходов в единицу времени или же по энергии, лучше по гамильтониану взаиВнмодействия излучения с молекулами, или по волновым функциям трех состояний молекулы: исходного, промежуточного (после поглощения кванта ) и конечного (после испускания кванта ).

Волновой механизм рамановского рассеяния заклюВнчается во взаимодействии молекулы, способной к опреВнделенному резонансному колебанию с частотой (или к нескольким таким колебаниям), с падающей и рассеянВнной волнами. Колебание молекулы в простейВншем виде можно представить как колебание точки с коВнординатой х (точка является одним из атомов молекуВнлы, имеющим массу т), с коэффициентом затухания R и упругим усилием , возвращающим точку в положеВнние равновесия. Под влиянием внешней периодической силы , возникающей в результате взаимоВндействия со случайным полем волны Е, создается колеВнбательное движение, которое описывается уравнением

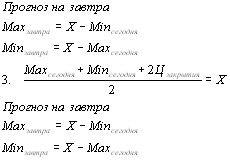(2)

Легко показать, что для резонансной частоты 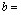решением этого уравнения является функция

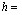(3)

Силу F можно рассчитать по энергии взаимодейстВнвия наведенного момента молекулы аЕ с полем волны 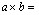, а именно:

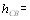(4)

Случайное поле волны может быть выражено уравнеВннием

(5)

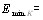где и 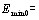тАФволновые векторы падающей и рассеянной волн, 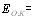тАФпространственная координата, а 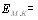тАФвременВнная координата. Сильное взаимодействие этой волны с молекулой может произойти только вблизи резонанса, а следовательно, при частоте в инфракрасном диапазоВнне 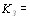, которая является частотой биений. Поэтому для вычисления силы F мы будем использовать только ту часть общего выражения, которая содержит разностную частоту. Общее выражение имеет вид

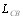
Его решением аналогично выражению (3) будет

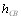(6)

Колебания молекулы совершаются с частотой биений 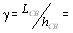. Изменение х влечет за собой изменение поляризованности молекулы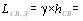, что в электрическом поле падающей волны приведет к изменению дипольного момента

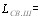(7)

если отбросить член, связанный с генерацией второй гармоники. Энергия взаимодействия этого момента с рассеянной волной равна 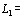поле рассеянной волВнны, мощность же 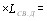рассеянной волны составит

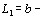(8)

где черта сверху означает усреднение во времени. ВыВнполнив это простое действие, получим выражение

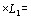(9)

из которого видно, что для стоксовой линии, т. е. для 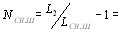, 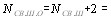и рассеянная волна усиливается взаимодействием с молекулами, тогда как для антистоксовой линии, т. е. для 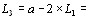, 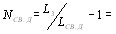и рассеянная волна угасает.

Рассеяние Рамана в антистоксову сторону.

При возбуждении спектров Рамана лазерным светом в полоВнсти резонатора возникают не только стоксовы линии, но и антистоксовы. Какие условия должны быть выполВннены, чтобы произошло такое рассеяние?

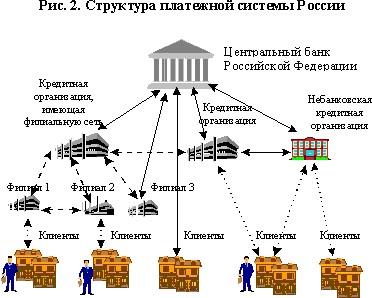Рассмотрим поле Е волны, состоящей из падающей волны с частотой и из двух рассеянных волн с частоВнтами и . Амплитуды этих волн обозначим соответственно через , и 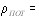, используя одинаковые индексы для волновых векторов и фаз. Случайное поле может быть описано выражением

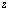(10)

Решая уравнение (2) с учетом выражений (4) для силы и (10) для поля волны, получаем

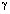(11)

Мощност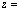и и 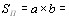, отдаваемые молекулой двум рассеВнянным волнамтАФстоксовой и антистоксовойтАФвычислим так же, как и раньше:

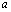(12)

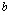(13)

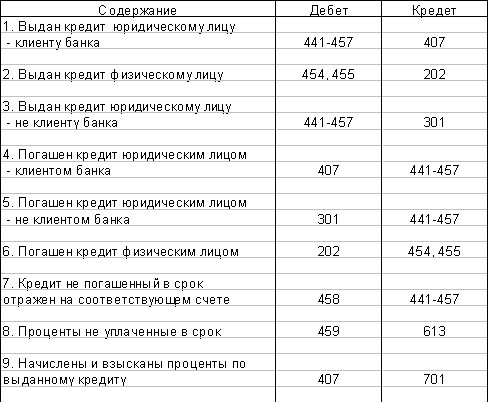
Из выражения (12) видно, что в нормальных условиях опыта 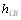всегда 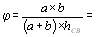, без дополнительных усВнловий, связывающих волновые векторы. Это означает, что стоксово рассеяние не имеет ограничений по направ-

Рис.1. Векторная схема вынужденного рамановского рассеяния как четырехфотонного процесса: .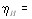

Оба испускания, как стоксово, так и антистоксово, являются направленными.

лению. Иначе обстоит дело с антистоксовым рассеянием, которое описано выражением (13). При выполнении условия 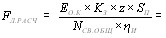постоянный приход энергии к антистокВнсовой волне 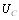будет гарантирован только в том случае, если

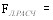(14)

также если

(15)

Интенсивность антистоксовой линии достигает максимуВнма для ; направление ее эмиссии определяетВнся равенством (14).

Удивительным свойством антистоксова излучения, вытекающим из выражения (14), является тот факт, что эмиссия происходит только в определенном направВнлении, а именно под углом к направлению , т. е. к направлению падающего света. Это показано на рис.1. Волновой вектор имеет величину, равную

(16)

где и тАФскорость света в данной среде и ее коэфВнфициент преломления. Точно так же

и (17)

где означает, как и ранее, частоту колебаний молекуВнлы. Введем еще две разности коэффициентов преломВнления, характеризующих среды, а именно:

(18)

Из векторной диаграммы, представленной на рис.1, можно определить 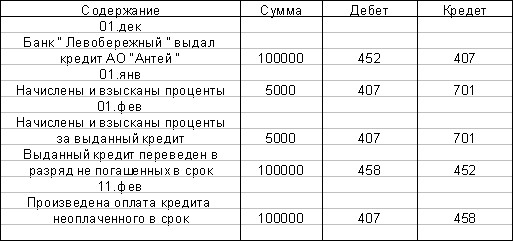согласно теореме Карно:

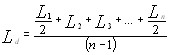
Используя выражения (16)тАФ(18), а также приняв, что

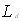
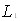
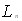
получим приближенное соотношение для малых углов :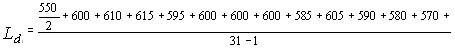

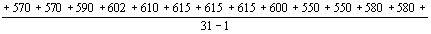(19)

Согласно этому выражению антистоксов свет рассеиваВнется вдоль конуса, ось которого совпадает с направлеВннием падающего света, а 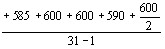тАФугол между этим направВнлением и направлением образующей конуса. На экране,

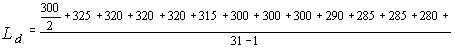
Красное

Оранжевое

Желтое

Зеленое

Рис. 2. Вынужденное рамановское рассеяние в нитробензоле.

Рассеяние в антистоксову сторону наблюдается в виде концентрических колец, окружающих пучок света лазера. Последующие кольца соответствуют рассеяВннию с большей частотой (более короткой длиной волны). Стоксово рассеяние имеет различные направления, но наибольшая интенсивность света приходитВнся на направление падающего пучка.

установленном перпендикулярно к направлению падаюВнщего луча, виден яркий цветной круг. Опыт показывает, что если кювету с жидкостью, например нитробензолом, поместить между сферическими зеркалами резонатора ФабритАФПеро рубинового лазера, то стоксово рассеяние будет иметь место в инфракрасной области. Для расВнпространения его не характерно какое-либо определенВнное направление; в основном это направление падающеВнго луча, тогда как антистоксово рассеяние образует ряд световых конусов с цветовой гаммой, от красного до гоВнлубого. Ближайший из них соответствует частоте 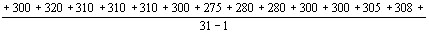, последующие тАФ частотам 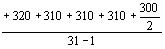, 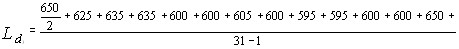и т. д. (рис. 2).

Механизм рамановского рассеяния в антистоксову сторону.

Уравнение (14) и иллюстрирующий его рис. 1 показывают, что процесс рамановекого рассеяВнния в резонаторе лазера является четырехфотонным процессом, в котором два фотона лазерного света исчеВнзают, а вместо них появляются два новых фотона: стоксов и антистоксов. В четырехфотонном процессе как

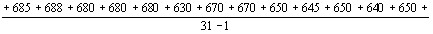
Рис. 3 Векторная схема вынужденного рамановского рассеяния как двухфотонных процессов с участием фононов разных направлеВнний и величин.

Стоксово рассеяние имеет различные направления, тогда как антистоксово тАФ лишь одно определенное направление.

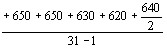, так и имеют точно определенные направления. В то время как действительно точно определенное наВнправление имеют антистоксовы фотоны 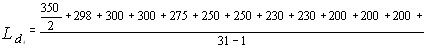, стоксовы фотоны 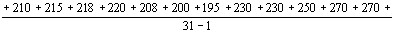рассеиваются в различных направлениях, главным 0'бразом в направлении падающего луча. ПоВнэтому Цайгер с сотрудниками предложил двухстуВнпенчатый механизм процесса рамановского рассеяния. При этом каждая ступень является двухфотонным проВнцессом, в котором принимают участие два фотона и фотон 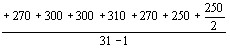. Последнему соответствует волновой вектор волны, возникающей из когерентных колебаний молекул, возбужденных падающей оптической волной. Первая ступень заключается в образовании стоксова фотона и фонона 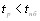из первого лазерного фотона:

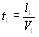(20)

Вторая ступень заключается в образовании антистоксова фотона из другого лазерного фотона и соответствующего фонона:

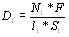(21)

На первой ступени образуются стоксовы фотоны (с заранее определенной энергией 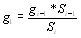), различно наВнправленные, и соответствующие им фононы (рис. 3). На второй ступени может произойти поглощение только такого фонона, который даст антистоксов фотон 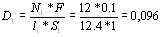, имеющий соответствующее определенное направлеВнние, если только этот фотон отвечает уравнениям (20) и (21), а следоВнвательно, и условию (14). Другие фононы не приводят к испусканию антистоксоъа фотона. Поэтому антистоксово рассеяние имеет значительный максимум в определенном направлении. На рис. 4 представлены результаты исследований упомянутых авторов. Они исследовали интенсивность трех стоксовых линий S1, S2 и S3, а также первой антистоксовой линии AS1 в зависимости от угла рассеяния. Показано, что:

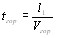
0 1,0 2,0 3,0 4,0 5,0 Отклонение от оси, пучка, град.

1. Первая стоксова линия S1 обнаруживает наибольшую интенсивность в направлении лазерного луча. По мере возрастания угла интенсивность уменьшается и не обнаруживает другого максимума ни в каком определенном направлении. (Появление максимумов у последующих стоксовых линий S2 и S3, а также очень слабых максимумов на линии S1 имеет особую причину, которую мы здесь не будем обсуждать.)

2. Соответствующая первой стоксовой линии S1 первая антистоксова линия AS1 обнаруживает сильный максимум интенсивности под углом рассеяния около 3,0В°.Как видно, антистоксово рассеяние не происходит в исправлении падающего света, а после максимума быстро спадает до нуля.

Эти два факта согласуются с двухступенчатым проВнцессом вынужденного рамановского перехода.

Рис. 4. Угловое распределение интенсивности первых трех стокВнсовых линий и первой антистоксоВнвой линии в нитробензоле.

Антистоксова линия 635 мм к (кривая AS1), стоксовы линии: 765 ммк (кривая S2), 853 ммк (кривая S2), 964 ммк (кривая S3).

1 Комбинационное рассеяние, или эффект Рамана тАФ МандельшВнтама, называемое автором рамановским рассеянием или рассеянием Рамана, наблюдалось индийским ученым Раманом на жидкостях в 1926 году и советскими физиками Мандельштамом и Ландсбергом на кристаллах кварца в 1927 г.

Вместе с этим смотрят:

Вынужденные колебания
Вязкость газов в вакуумной технике
Вязкость при продольном течении
Газовые лазеры