Проблемы подготовки к экзаменам

Часть 2. Проблема подготовки к экзаменам.

I. Введение

С данной проблемой сталкивался каждый студент. Проблема заключается в рациональном распределении времени на подготовку к экзаменам, с учетом сложности, важности предметов, сдаваемых на экзамене. Существует несколько рекомендуемых методик подготовки к экзаменам, но лишь некоторые из них математически обоснованы. Данная работа предоставляет метод определения оптимального графика подготовки к экзаменам с учетом наиболее важных факторов. Общий подход данной работы предполагает, что залог успешной сдачи экзамена на требуемую оценку - изучение литературы по предмету экзамена в должном объеме. Поэтому результаты и рекомендации, полученные при использовании приведенного здесь метода, могут противоречить позициям других методик подготовки к экзаменам.

II. Математическая модель задачи.

Общие положения.

Данная модель использует понятие "время", которое по смыслу практически эквивалентно понятию, используемому в повседневной жизни. Выбор како-то конкретной единицы времени в данной модели ограничен лишь соображениям точности.

Данная модель, как уже было сказано, учитывает лишь степень овладевания материалом данного экзамена. При этом полагается, что длительность подготовки является основным фактором, влияющим на степень овладевания материалом данного экзамена. Также данная модель предполагает, что все предметы понимаются человеком с разной успешностью. Кроме этого предположения вводится предположение о том, что материал каждого предмета запоминается человеком по разному. Данная модель построена на ценности того или иного события. С помощью различных методов суммарное значение ценностей максимизируется. Следует также отметить, что большинство параметров, учитываемое при подсчете ценностей, субъективно.

Пусть N - количество экзаменов, которое предстоит сдать. В дальнейшем для ссылки на какую-либо характеристику определенного экзамена будет применяться индекс i, i=1.N.

Пусть также объективно задано время, когда можно начинать готовиться к i-ому экзамену tiн, а также время, до которого можно готовиться - tiк. В большинстве практических ситуаций оно будет эквивалентно времени начала сдачи самого экзамена. Время начала подготовки к сессии - t0 - может быть определено как минимальное из времен tiн.

t0= min ( tiн) , i=1.N

Естественным ограничением на времена tiн и tiк является

tiк - tiн > 0.

За конец сессии примем максимальное значение tiк

te=max tiк.

За длительность сессии l примем величину

l=te -t0.

Также для каждого экзамена должны быть заданы следующие величины: Ei - коэффициент успешности сдачи экзамена, Мi - коэффициент запоминаемости материала экзамена, Ii - коэффициент значимости получения желаемой оценки на данном экзамене, Q0i - объем знаний, необходимый для получения желаемой оценки без учета случайностей, Ui - коэффициент понимания человеком данного предмета. Все эти коэффициенты - субъективные, а поэтому и индивидуальны для каждого человека. Данные величины в общем случаи различны для каждого экзамена. Входным параметром также является величина ценности свободного времени L0.

Далее будут подробнее рассмотрены данные коэффициенты и методы их определения.

Ei - коэффициент успешности сдачи экзамена.

Еi>=0. Данный коэффициент определят, насколько легко можно сдать экзамен при относительно низкой подготовке. Ei=0 соответствует типу экзамена, когда он оценивается строго, без натяга оценки, поблажек - то есть при полностью субъективной оценке экзаменатора. На значение данного коэффициента влияют возможность списывания у соседа, использования шпаргалок, подсказки или натяжки оценки со стороны преподавателя, а также некоторые другие факторы.

Мi - коэффициент запоминаемости материала экзамена.

Коэффициент запоминаемости материала экзамена тесно связан с Ui - коэффициентом понимания человеком данного предмета. На их значения галагаются следующие ограничения:

0<=Mi<=1. Ui>= 0.

Использование этих моделей связано с введением дополнительной модели усваивания материала человеком. Модель, специально разработанная для данной работы, базируется на понятии объем знаний.

Предполагается, что каждый предмет усваивается человеком со свойственной ему эффективностью. Эффективность понимания материала - величина относительная. С течением времени происходит процесс забывания материала. Рассуждая таким образом, можно приближенно представить процесс получения знаний формулой

Q = U (1 - Mt ),  (1)

где Q - объем знаний,

U - коэффициент понимания,

M - коэффициент забывания материала - в единицу времени.

t - время, оставшееся до теста по усвоенным знаниям.

Данная формула приближенно описывает процесс приобретения знаний человеком. При U=0 (человек вообще не понимает данный материал) - объем знаний равен 0. При больших значениях M человек спустя некоторое время забудет всю полученную информацию (пора идти к врачу). При М=0 человек ничего не забывает. При t-> 0 объем знаний будет максимальным (человек забыть ничего не успевает). Если человек использует время не только для учебы, то коэффициент понимания U следует уменьшить во столько раз,  в каком отношении человек занимается учебой относительно всего времени (полагается, что он отвлекается от подготовки с одинаковой интенсивностью в течении всего времени освоения материала). Общий объем знаний, полученный человеком за время с t1 по t2 будет выражаться интегралом

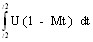     (2)

Коэффициенты Ui и Mi имеют тот же смысл, что и U и M в формуле (1).

Далее продолжается рассмотрение других входных параметров.

Ii - коэффициент значимости получения желаемой оценки на данном экзамене

Данный коэффициент - субъективная относительная величина, определяющая, во сколько раз больше студент заинтересован в получении желаемой оценки на данном экзамене к желанию получить желаемую оценку на наименее важном экзамене. Данный коэффициент >= 1. Соответственно, данная коэффициент для наименее важного экзамена =1.

Также наряду с Ii - коэффициент значимости получения желаемой оценки на данном экзамене, будет использоваться величина Ii' - приведенный коэффициент значимости получения желаемой оценки на данном экзамене. Он выражется как

Ii'= Ii/(1+Ei).

Его использование будет пояснено в дальнейшем.

Q0i - объем знаний, необходимый для получения желаемой оценки без учета случайностей.

Данная величина определят объем знаний, требуемый для сдачи экзамена на желаемую оценку. Определение данной величины связано со своего рода трудностями. Для простоты определим объем знаний Q0 как количество времени, требуемое для овладеваемое данным материалом при отсутствии забывания умноженное на объем знаний, полученный за единицу времени при M=0. Численно это будет произведением времени на U. Если студенту приходилось сдавать экзамен по данному предмету и по тому же материалу на желаемую оценку, то Q0i можно посчитать как интеграл за все время подготовки к данному экзамену при условии полной объективности поставленной оценки отсутствии случайностей и совпадений.

L0 - ценность свободного времени.

Данная величина указывает ценность свободного времени, не занятого подготовкой ни к одному экзамену. Величина может также трактоваться как нежелание учиться. Данная величина имеет размерность приведенного коэффициента значимости получения желаемой оценки и должна задаваться как отношение субъективной ценности 1 единицы свободного от подготовки к экзамену времени к значимости получения желаемой оценки на самом легком экзамене (Ii=1) при легкости данного экзамена = 1 (Ei=1).

Общие зависимости.

Общий эффект от подготовки к экзамену i (ценность) может быть выражен с использованием вышеописанных обозначений как

Ci = Qi*Ii/(Qi0*(1+Ei))=Qi*Ii'/Qi0      (3)

где Qi - суммарный объем знаний, полученный студентом за время подготовки.

Qi можно найти по формуле

Qi=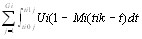    (4)

где Gi - количество интервалов времени, в течении которых студент готовится к экзамену i,

ti0j - время начала j-го интервала подготовки студента к экзамену i

ti1j - время окончания j-го интервала подготовки студента к экзамену i

Суммарная эффект С от всех экзаменов выражается суммой всех Ci.

Суммарная ценность свободного времени в течении сессии будет выражаться как

L=L0*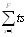     

где F - количество интервалов свободного времени

ts - длина интервала свободного времени s.

Наконец, суммарная ценность P, полученная студентом во время сессии выражается как

P=C+L (5)

Данное значение требуется максимизировать. Дополнительным условием по временам будет условие

#SUM s=1,F ts + #SUM i=1,N #SUM j=1,Gi ti1j-ti0j = l 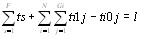  (6)

   (6)

Также никакие интервалы не должны пересекаться (7)

На языке динамического программирования данная задача заключается в  максимизации функции (5) при ограничениях (6) и (7).

1. Алгоритм решения задачи.

Общие зависимости.

Ограничение (7) делает задачу трудно решаемой в непрерывных величинах. Здесь же будет дан алгоритм приближенного решения методом назначений. Для использования этого метода следует перейти от понятия непрерывного времени к понятию дискретного. Введем величину дискретности времени. Разобьем интервал сессии длиной l на h частей. Длина каждого интервала будет равна dt=l/h. Далее заменим времена tiн и tik на соответствующие им tiн' и tiк', при этом для вычисления  будем использовать формулу:

tiн'=(tiн-t0)/dt

tiк'=(tiк-t0)/dt

Полученное рациональное число будем округлять внутрь интервала: tiн'  в большую сторону, tiк' в меньшую. Далее в задачу о назначениях введем h кандидатов и W+h работ - количество работ будем рассчитывать по формуле

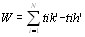
Каждому i-ому экзамену будет соответствовать (tiк'-tiн') работ. Работы с индексом от W до W+h соответствуют отдыху (отсутствию учебы) в данный интервал времени.

Заполнение матрицы стоимостей задачи назначений.

Для работ, соответствующих отдыху : сxy, y>W  cxy=L0*dt

сxy: y-> i.(в соответствии с номером работы y находим номер i соответствующего ей экзамена.

x < (tiн-t0): cxy=0

(tiн-t0) <= x <= (tiк-t0): cxy= Qix*Ii'/Qi0, Qix=U*dt*(1 - M(tiк' - x)

x > (tiк-t0): cxy=0

В большинстве случаев количество работ не будет равно количеству кандидатов. Если используемое программное обеспечение в явном виде не позволяет решать несбалансированные задачи о назначениях, то нужно добавить фальшивых кандидатов или работы.

Далее находим максимум задачи о назначениях. Если используемое программное обеспечение в явном виде не позволяет находить максимум, то инвертируем знаки элементов матрицы и подвергаем полученную матрицу минимизации.

Интерпретация полученного ответа.

График подготовки к экзаменам на основе полученного результата строится следующим образом:

Для каждого x-ого кандидата (x=1.h)

Определяем индекс y работы, на которую назначен данный кандидат x.

интервал времени (t0;t0+dt*x) должен быть посвящен

• Если y>W, то отдыху.
• Если нет, то по индексу y определяем индекс i экзамена, который соответствует y-ой работе. Данный интервал должен быть посвящен подготовке к экзамену i.

Замечания

1. Для обеспечения более высокой точности требуется уменьшить дискретность единицы времени.
2. Данная модель не пригодна для экзаменов, подготовка к которым не заключается в изучении литературы и практических занятиях, к примеру, по физкультуре. При наличии экзаменов данного типа в сессии их просто не надо включать в список.
3. Данная модель не учитывает время, необходимое человеку для перенастройки с одного теоретического материала на другой. В принципе данная особенность не должна сказываться на результатах, так как дискретность времени при решении методом назначений вносит гораздо большую погрешность.
4. Данная модель предполагает, что все источники информации доступны обучающемуся, т.е. у него есть вся необходимая литература.
5. Данная модель не учитывает всевозможные психологические состояния человека, а также влияния эмоций от сданных экзаменов.

Вместе с этим смотрят:

Профессиональное самоопределение старшеклассников
Профориентация и понятие профпригодности
Процесс общения и трансакционный анализ
Психоанализ