Автоматизированная система распределения мест и оценок качества олимпиадных заданий

Новая шкала ценностных приоритетов, отражающая государственную политику и отношение педагогической науки к образованию, является на сегодняшний день главным фактором, определяющим необходимость реформирования школьной системы образования и перехода к 12-летней школе. Ожидаемые в связи с этим преобразования носят достаточно существенный характер, поскольку предполагают Влосуществление принципиально другой направленности образования, связанной не с подготовкой ВлобезличенныхВ» квалифицированных кадров, а с общим, социально-нравственным и профессиональным развитием личностиВ».

Радикальность предстоящих перемен, в процессе которых во главу угла предполагается поставить создание условий для максимально полной самореализации каждого учащегося и свободного развития его личности, делает весьма актуальным вопрос о порядке реформирования традиционной системы образования, базирующейся в основном на ВлзнаниевойВ» парадигме. Совершенно очевидно, что режим Влшоковой терапииВ» в данном случае абсолютно неуместен.

Единственно верным в создавшейся ситуации представляется путь последовательного и щадящего реформирования, предполагающий не безоглядную ломку сложившейся системы образования, а ее приспособление к решению новых задач с сохранением всего ценного, что она накопила. При таком подходе большую значимость приобретает проблема педагогического моделирования, результаты которого могут служить аргументированным основанием как для сохранения накопленного потенциала традиционной системы образования, так и для выбора форм и методов ее реформирования. Особый интерес в этой связи приобретают случаи, когда педагогическое моделирование ведется в количественном виде и сопровождается установлением функциональных и корреляционных соотношений, связывающих конечные педагогические показатели с параметрами образовательного процесса и исходными характеристиками учебно-воспитательного коллектива. Именно они способны обеспечить доказательность и оптимальность выбираемого пути реформирования педагогического процесса и его приспособления к решению изменившихся задач.

В настоящей работе приводятся результаты исследований, посвященных проблеме педагогического моделирования интеллектуального испытания школьников. В арсенале педагогических методов и средств интеллектуальному испытанию принадлежит одно из важнейших мест. В режиме интеллектуального испытания, например, проходит большинство способов контроля уровня знаний учащихся (опросы, контрольные и самостоятельные работы, экзамены, тесты). Интеллектуальное испытание лежит в основе мероприятий соревновательного характера олимпиад, викторин, конкурсов. Без интеллектуВнального испытания учащихся невозможно представить себе не только проблемВнное, но и традиционное обучение, поскольку сам процесс обучения, если гоВнворить по большому счету, ведется в форме распределенного во времени инВнтеллектуального испытания учащихся. При этом студенты, не выдерживающие этого испытания, просто отчисляются из вуза, а школьники переводятся на более щадящий режим обучения, например, в классы коррекции.

Очевиден и воспитательный аспект интеллектуального испытания, котоВнрое можно рассматривать как определенную форму воздействия на испытуеВнмого школьника. Тот факт, что режим этого воздействия задается непосредВнственно педагогом, превращает интеллектуальное испытание в инструмент формирования личности учащегося, его характера, способности к самооргаВннизации и концентрации усилий на преодоление трудностей. С этой точки зрения, интеллектуальное испытание являет собой пример управляемого треВннинга, подготовки школьника к будущей ВлвзрослойВ» жизни, представляющей собой, как известно, бесконечную цепь весьма непростых испытаний.

Выбор олимпиады школьников в качестве предметной базы для отработки педагогической модели интеллектуального испытания обусловлен целым ряВндом обстоятельств. Здесь, в первую очередь, следует отметить простоту и проВнзрачность олимпиады как педагогического мероприятия с четко определенВнным регламентом, в рамках которого многие педагогические проблемы приВнобретают смысл, доступный для описания на языке количественных соотноВншений. Вторым обстоятельством, выделяющим олимпиаду в качестве оптиВнмального объекта педагогических исследований, является уникальность анВнсамбля ее участников, представляющего простейшую педагогическую систеВнму, образованную ВлмеханическимВ» соединением школьников. Данная систеВнма действительно уникальна. Она характеризуется заведомой аддитивностью своих свойств и соответствует наиболее простой (если не сказать самой примитивной) форме взаимоотношения личности и коллектива, выражающейся в элементарном сложении.

Простота олимпиады заключается еще и в небольшом разбросе ее участВнников по уровням подготовки (все они в большинстве своем хорошо успеваВнющие школьники). Это создает условия для использования линейных приВнближений, что значительно упрощает математическое описание. МоделироВнвание итогов олимпиады облегчается тем, что распределение участников по способностям известно априори. В силу многоэтапного характера олимВнпиады оно соответствует распределению отобранного ансамбля, в котором основную массу испытуемых составляют именно ВлспособныеВ» учащиеся, поскольку малая доля Влистинно талантливыхВ» школьников определяется чисВнто объективными причинами, а незначительное представительство в ансамбВнле Влоткровенно слабыхВ» учащихся - их отсевом на предыдущих этапах.

Олимпиада школьников в дополнение ко всему является чрезвычайно удобВнным объектом не только для теоретических, но и для экспериментальных пеВндагогических исследований. По отношению к проблеме интеллектуального испытания она является готовым экспериментальным полигоном. С одной стороны, циклический характер олимпиады и практически неизменный поряВндок ее проведения обеспечивают благоприятные условия для долговременноВнго констатирующего эксперимента по изучению параметров интеллектуальВнного испытания, необходимых при формулировке исходных позиций моделиВнрования. С другой стороны, автономия отдельных этапов олимпиады предосВнтавляет составителям заданий и организаторам олимпиад достаточно широВнкие возможности для формирующего этапа эксперимента, связанного с апроВнбацией модели и внедрением модельных разработок в практику проведения олимпиад. Многоуровневая структура олимпиады в сочетании с иерархичесВнкой взаимосвязью отдельных этапов обеспечивает при этом широкомасштабВнный характер исследований как на пассивной, так и на активной стадиях эксВнперимента. Она позволяет работать с большими статистическими ансамбляВнми, представляющими в то же самое время соединение весьма разнообразВнных выборок учащихся. Это обеспечивает необходимую репрезентативность и достоверность получаемых экспериментальных результатов.

Непосредственную опытную базу настоящего исследования составили региональные физические олимпиады школьников, проходившие в Рязани в 2003 г., а также ведомости успеваемости студентов физико-математического факультета по разным предметам. Это дало возможность судить о гуманности преподавания на тех или иных кафедрах Рязанского педагогического университета им. С. А. Есенина. Кроме того, в настоящем исследовании были использованы материалы, взятые во время прохождения педагогической практики в средней школе №43 г. Рязани.

Вз2. Цель работы.

Работа полностью опирается на теоретические исследования Б. С. Кирьякова, и была призвана дополнить их. С самого начала передо мной ставилась задача превратить эти исследования, а также накопленную в них математическую базу, в нечто осязаемое, то есть попросту упростить тот процесс обработки экспериментальных результатов, который предлагает сам автор теории. Таким образом, целью данной работы можно считать разработку автоматизированной системы распределения мест и оценки уровня качества олимпиадных задач по физике. При выполнении работы, мною была разработана специальная программа, которая инкапсулирует в себе ту математическую теорию, которую разработал Б. С. Кирьяков. Совместно с ним была произведена проверка данной программы на примере городской олимпиады по физике в 11 классах. Кроме этого, в качестве эксперимента, через программу ВлпрогналиВ» и ведомости студентов физмата по некоторым дисциплинам. При этом были получены очень интересные результаты, о которых речь пойдет ниже.

Вообще говоря, разработанная программа может оказаться полезной не только на олимпиадах. Она может помочь и на простых уроках, причем по любым предметам.

Математическая теория, лежащая в основе программы, оперирует достаточно простыми понятиями, и, в принципе, может быть понятна рядовому учителю. Однако необходимости в изучении азов нет, так как не каждому педагогу интересна начинка какого-либо сложного с первого взгляда объекта, а большую важность здесь имеет результат. Собственно говоря, программа и призвана для получения конкретного результата без акцентирования на деталях расчета, а если этот результат представлен визуально, то это дополнительный плюс всей системе.

Глава 2. Проблема распределения мест на олимпиаде и ее решение. Оценка уровня качества олимпиадных заданий.

Вз1. Теория распределения мест. Проблема дифференцированного подхода.

Проблема автоматизированного распределения мест на олимпиадах не нова. Существуют определенные системы распределения мест во многих странах мира (например, в США), и все они имеют ряд очевидных преимуществ по сравнению со стандартной схемой.

Первое (и самое главное) преимущество тАУ отсутствие Влчеловеческого фактораВ» при этой процедуре. Машине чужды эмоции, она бесстрастна, а что еще нужно для грамотной постановки вопроса. К тому же, в связи с широким, в последние 5 лет, распространением компьютерной техники в России, разработка таких систем является достаточно перспективной областью.

Второе преимущество тАУ это так называемый Влфактор времениВ». Всем известно, что любая школьная (городская, областная и т.д.) олимпиада тАУ это дело долгое. Сначала участники выполняют задания, потом жюри оценивает их, а далее следует процесс сортировки работ по местам, причем, чем больше участников на олимпиаде, тем больше времени этот процесс занимает. В школе это время небольшое, но в масштабах области или страны это может занять очень много времени. Машина же выполняет этот процесс гораздо быстрее, и время на сортировку можно сократить на порядок, а то и два.

Скажем сразу тАУ полностью автоматизированной системы для проведения олимпиад, их оценки, распределения мест нет, хотя проекты такие существуют. Машина пока может лишь работать с данными, которые в нее вводит человек. В будущем, возможно, будут созданы системы, которые сами будут проверять задания, оценивать их, распределять места и т.д., а человек будет лишь контролировать эту деятельность и пожинать ее плоды.

Вот к чему на данном этапе все стремятся, однако это не так просто как кажется. Поэтому мы остановились на обычной системе, работающей с протоколом, который вводится оператором. Исходя из данных, которые содержатся в этом протоколе, программа получает конечный результат и визуализирует его, но об этом ниже.

Теперь немного теории.

Распределение участников олимпиады по занимаемым местам происхоВндит на заключительной стадии олимпиады. Именно здесь определяются приВнзеры, представляемые к награждению, и участники, допускаемые к выходу на следующий этап олимпиады. Отвечает за распределение мест обычно предВнседатель предметного жюри.

Фактическую базу, определяющую распределение мест, образуют итоги олимпиады, отражающие успехи школьников в решении олимпиадных задач. Обычно их представляют в виде (1):

x₁, x₂, x₃, тАж,x_i, тАж, x_n, (1)

где x_i= 0, 1, 2, тАж, m тАУ баллы, набранные участником за задачу с номером i.

Распределение мест непосредственно проводят не по итогам решения отВндельных задач (1), а по некоторым показателям ή₁, ή₂, ή₃, .., характеризуВнющим выполнение олимпиадного задания в целом:

(ή₁, ή₂, ή₃, ..)=║П║(x₁, x₂, x₃, тАж) (2)

где ║П║ − некоторые преобразования, переводящие описание итогов олимпиаВнды с языка переменных х₁,х₂,х₃,тАж (равных набранным баллам за отдельно взятые задачи), на язык показателей ή₁, ή₂, ή₃, .., характеризующих выполВннение всего олимпиадного задания.

Показатели ή₁, ή₂, ή₃, .., определяющие распределение мест, удобно называть показателями приоритета. Одним из таких показателей, как извеВнстно, является суммарный балл:

S=х₁+х₂+х₃ + .. + х_i+.. + х_n(3)

В общем, порядок распределения участников соревнования по месВнтам при множественном числе показателей приоритета определяется выбоВнром самих показателей ή₁, ή₂, ή₃, .., их числом l и логикой приоритета, определяющей место участника олимпиады в соответствии с численными значениями показателей ή₁, ή₂, ή₃, .. . С формальной стороны использоваВнние нескольких показателей при выстраивании какой-либо одномерной очеВнредности объектов не создает больших сложностей. Для этого достаточно один показателей считать ВлглавнымВ», второй − ВлвторостепеннымВ», третий − ВлтретьестепеннымВ» и т.д. При распределении мест главный показатель ή₁ следует принимать во внимание в первую очередь, второстепенный ή₂ при равенстве главных, а третьестепенный ή₃ при одновременном равенстве главных и второстепенных показателей и т.д.

Подобное распределение очень часто используется в спорте. Примером того может служить распределение футбольных команд по итогам чемпионата, которое проводят по двум показателям − по числу набранных очков (главный показатель) и по разнице между забитыми и пропущенными мячами (второстепенный показатель).

Однако это только формальная сторона дела. Вся сложность проблемы заключается в том, что ввести отмеченную иерархию показателей приоритета (ВлглавныйВ», ВлвторостепенныйВ» и т.д.) достаточно непросто. Особенность ситуации состоит в том, что формальная логика распределения мест при множеВнственном числе показателей

l≥2(4)

оказывается внутренне противоречивой. Данное противоречие кроется в равноправной возможности двух подходов к распределению мест между участниками олимпиады − одного с ориентацией на большее удаление от ВлабсоВнлютного аутсайдераВ» (участника, не набравшего ни одного балла), другого с ориентацией на наибольшее приближение к Влабсолютному лидеруВ» (участниВнку, давшему исчерпывающее решение всех задач),

Отмеченное противоречие не имеет места при одном показателе приориВнтета ή₁. В этом случае каждый участник, набирая баллы по задачам и удаляясь от аутсайдера, неминуемо приближается к лидеру.

Подобная однозначность, как это ни странно, не является достоинством. Достаточно вспомнить, что распределению подвергаются не абстрактныеобъекты, а школьники. Распределение по местам подростков и юношей, отяВнгощенных комплексом проблем своего возраста, можно проводить лишь с учетом соображений психолого-педагогического характера, которые по своВней сути являются вариативными, зависящими от конкретной ситуации. При одном показателе приоритета условий для подобной вариативности, а соотВнветственно и для дифференцированного подхода нет. Все однозначно опредеВнляется формальной логикой, а соображения психолого-педагогического хаВнрактера просто некуда включить.

Однако руководствоваться соображениями только формальной логики нельзя. Данная ситуация представляется чрезвычайно интересной. Ее уникальность заключается в том, что она соответствует условиям, когда необходимо привлечение педагогических соображений к распределению мест. Понятна и роль, отводимая при этом педагогике. Это роль Влтретейского судаВ», который в рамках сложившегося противоречия может стать на одну из двух взаимоисключающих точек зреВнния, руководствуясь соображениями педагогической целесообразности.

Ситуация соответствует случаю, когда возможный порядок распределения мест таков, что приоритет численных значений покаВнзателя ή₁, определяется формальной логикой, а приоритет значений показатеВнля ή₂ − педагогической целесообразностью. В силу вариативного характера педагогических соображений данное распределение можно провести диффеВнренцированно, меняя точку зрения на приоритет значений ή₂ по отношению к каким-то выделенным группам школьников.

Отмеченные ВлвзаимоотношенияВ» показателей ή₁ и ή₂говорят о логическом главенстве ή₁. При распределении мест его необходимо рассматривать в качестве главного показателя и принимать во внимание в первую очередь, а показатель ή₂ − в качестве второстепенного и учитывать лишь при равенстве значений ή₁.

Приведенные выше соображения говорят о том, что дифференцированВнный подход к участникам олимпиады в рамках ее регламента вполне возмоВнжен. Он может быть реализован лишь на стадии распределения мест, но тольВнко в том случае, когда оно проводится по нескольким показателям приоритета (4). Одного главного показателя ή₁, определяющего приоритет выполненВнного задания с позиций формальной логики, для этого недостаточно. ПедагоВнгические соображения, обеспечивающие дифференцированный характер расВнпределения мест, могут быть учтены лишь с помощью второго, третьего и других показателей более высокой степени.

Смысл главного показателя приоритета ή₁ вполне ясен. Суммарный балл (3) способен исполВннять роль лишь главного показателя приоритета ή₁, и в принципе не может служить предметной базой для дифференцированного подхода.

Возможность использования величины ή₂= x₁−x₂ (5) в качестве второстепенного показателя приоритета, дополняющего суммарный балл ή₁ (4), достаточно очевидна. Если суммарный балл ή₁ определяет выполнение задания с количественной стороны, то показатель ή₂ (5) характеризует качество выполнения задания. Он показывает, в решении какой из задач (простой или сложной) участник больше преуспел.

Множественный характер показателей приоритета является свидетельством самой возможности дифференцированного подхода. С этой точки зрения соотношение (4) можно рассматривать как необходимое условие, определяющее соответствие используемой системы распределения мест требованиям дифференцированного подхода. Следует отметить, что в условиях рязанских региональных олимпиад условие (4) никогда не выполнялось. Места традиВнционно распределялись с использованием лишь одного показателя приоритеВнта - суммарного балла S (3), что не дает никаких оснований даже говорить о дифференцированном подходе.

В общепедагогическом плане пренебрежение дифференцированным подходом может вызывать лишь глубокое сожаление. Олимпиада, являясь педаВнгогическим мероприятием, должна заниматься не только констатацией споВнсобностей участников на момент ее проведения, но и заботиться о создании мотивационной базы для развития скрытых потенциальных возможностей учащихся. В первую очередь, здесь следует обращать внимание на участников, которые выступили на олимпиаде пока еще не совсем удачно. Этих школьниВнков необходимо поддержать и отметить хотя бы самые малые их успехи на олимпиаде, подкрепив все соответствующим поощрением по соображениям педагогического характера. Дифференцированный подход к распределению мест, возможный при выполнении соотношения (4), создает для этого все необходимые условия.

Следует отметить, что введение множественного числа показателей приВноритета, определяющих саму возможность дифференцированного подхода, не может быть произвольным. Для этого необходимы различаемые этапы реВншения задач или различаемые задачи (что несколько предпочтительнее). ИменВнно по этой причине для олимпиады должны быть использованы разноуровневые задачи (2). Только различие этих заВндач сделало понятным смысл ή₂ (5) как показателя поляризации способВнностей школьника. Для одноуровневых неразличимых задач показатель ή₂ (в отличие от ή₁, характеризующий выполнение задания с количественной стороны) потерял бы всякий смысл, что сделало бы невозможным его использование как показателя приоритета.

В нашем случае мы ограничиваемся лишь тремя показателями приоритета ή₁, ή₂ и ή₃ при распределении мест, чего вполне достаточно для нашей задачи. Смысл этих показателей достаточно прозрачен. Показатель ή₁, как показано выше, тождественен суммарному баллу и сам по себе не может быть использован в качестве критерия для распределения мест. Показатель ή₂ характеризует успехи школьника в репродуктивно-продуктивной деятельности по сравнению со средним арифметическим значением его успеВнхов за отдельно взятые испытания репродуктивного и продуктивного харакВнтера. Он показывает, насколько соединение способностей школьника отличаВнется от их простого арифметического сложения. Показатель же ή₃ характеризует поляризацию способностей школьника, представляя его достижения в решении творческих задач, рассчитанных на продуктивную деятельность, в сравнении с успехами в решении типовых задач, носящих репродуктивный характер. Все три показателя являются целыми числами, что существенно облегчает процесс расчета.

Таким образом, имея результаты олимпиады (или, например, сессии), можно точно подсчитать эти три показателя, исходя из них, можно с большой точностью говорить о распределении мест. Здесь возникает еще один вопрос: какой из показателей главный, а какие второстепенный и третьестепенный? Частично эта проблема решена выше, но там описывались только два параметра. Решение здесь может быть таким. Необходимо вводить несколько Влдифференцированных подходовВ» на базе значений показателя ή₁ (так как он является основным и главным для других). Если значения ή₁ для большей части (или для всех) участников отрицательны (это говорит о потенциальной слабости испытуемого коллектива), то имеет смысл за второстепенный показатель принять ή₂, а за третьестепенный тАУ ή₃. Проще говоря, в этом случае мы акцентируем внимание на репродуктивные (типовые) задачи, которые, по логике вещей, участники должны решить. Продуктивные (творческие) же задачи мы как бы не учитываем вообще в силу того, что такой коллектив может их не решить вообще. Например, таким ансамблем является коллектив школьников, представленный в программе в базе dbolymp1. Это условно первый вариант дифференцированного подхода.

Возможен вариант, что значения ή₁ для всех участников только равны нулю или положительны (это признак сильного коллектива). В этом случае за второстепенный показатель приоритета имеет смысл принять ή₃, а за третьестепенный тАУ ή₂. Другими словами, здесь мы делаем упор именно на продуктивные задачи (они обычно сложнее), а решение типовых задач считаем саморазумеющимся. Этот подход можно назвать вторым методом дифференцированного подхода.

И, наконец, самый интересный случай тАУ ή₁ для всех участников принимает и нулевые, и положительные, и отрицательные значения. Здесь процесс распределения мест несколько усложняется, так как во всем количестве участников присутствуют и потенциально сильные ученики, и слабые. Понятно, что всех их сортировать только одним из способов нельзя (исчезает главный принцип дифференцированного подхода), поэтому мы прибегаем к комбинационному методу. Суть метода такова. Все многообразие участников делится пополам, исходя из значений ή₁. Тех участников, у которых ή₁≥0, относят к условно ВлсильнойВ» группе и для сортировки используют метод ή₁→ ή₃→ ή₂. Те же участники, у которых ή₁<0, попадают в условно ВлслабуюВ» группу, и для этой группы используют метод ή₁→ ή₂→ ή₃. Таким образом достигается полная реализация принципов дифференцированного подхода. Реально, олимпиадных коллективов с такой комбинацией значений параметра ή₁, практически не встречается. Это можно отнести к минусу составителей олимпиадных заданий, а можно тАУ к учителям, которые готовят школьников к олимпиадам. Это самый общий принцип дифференцированного подхода. Мы назовем его условно третьим методом. Этот метод, вообще говоря, применим всегда, так как видно, что он является сочетанием первых двух методов. Поэтому, всегда рекомендуется использовать именно его. В частности, разработанная система не требует вмешательства пользователя в процесс выбора типа метода, сама выбирает необходимый и сортирует, придерживаясь этого типа.

Сложно сказать, что должно быть в идеальном случае. С одной стороны, если сильных участников будет много тАУ это хорошо. С другой стороны тАУ можно с полной уверенностью сказать о том, что всегда будут и сильные, и слабые ученики. Единственное, о чем можно точно говорить тАУ модель, которая использовалась при построении теории, базируется на последнем варианте распределения.

Это было краткое введение в теорию распределения мест, которая использовалась при создании автоматизированной системы. Теперь, опять же с точки зрения теории, рассмотрим проблему оценки уровня качества олимпиадных заданий, что тоже в дальнейшем понадобится.

Вз2. О проблеме оценки уровня качества олимпиадных заданий.

Проблема оценки уровня качества олимпиадных заданий является достаточно интересной областью исследования на данном этапе. Понятно, что сейчас есть смысл говорить о качестве заданий, предлагаемых на олимпиадах по различным тематикам. Подобно тому, как любой продукт питания или элемент домашней техники должен удовлетворять каким-то определенным требованиям, олимпиадное задание должно также характеризоваться набором каких-либо параметров, которые, в свою очередь, должны характеризовать его качество и класс его составителя. Однако такие параметры для конкретного олимпиадного задания найти достаточно сложно или правильнее сказать практически невозможно. В этом случае реально можно использовать только один очевидный параметр тАУ сложность задачи. Но, с другой стороны, одна и та же задача может быть Влсложной по-разномуВ» для разных учеников. Здесь подразумевается то, что у задачи может быть разный ход решения, приводящий к правильному результату, и этот ход по-разному воспринимается разными учениками. Проще говоря, для одного ученика данная задача окажется очень легкой, а для другого тАУ нерешаемой, и говорить о сложности нет смысла. Однако в контексте данной теории все задачи условно делят на три группы: продуктивные (творческие), репродуктивные (типовые) и продуктивно-репродуктивные (типовые задачи с ВлизюминкойВ» или творческие с элементарным смыслом). При этом полагается, что решение продуктивной задачи вызовет у любого ученика большую сложность, чем решение репродуктивной.

Вообще говоря, необходимо понять то, что нужно оценивать качество не какой-то отдельной олимпиадной задачи, а пытаться оценить блок заданий на олимпиаде и всю ее целиком. Эта задача менее трудна, но тут тоже может встретиться ряд трудностей, главная из которых заключается в поиске адекватных педагогической теории параметров, при помощи которых эти самые задания и оцениваются. То есть необходимо вывести такие показатели, которые будут полностью объясняемы с точки зрения педагогики. После того, как эти параметры будут известны, смысл их с педагогической точки зрения понятен, необходимо попытаться определить оптимальный вид комплектации олимпиадных заданий по типам задач, при котором будет достигнут максимальный эффект. В этом, собственно говоря, и заключается смысл всей теории.

Вз3. Виды задач. Краткое описание каждого вида.

Как уже отмечено выше, в рамках теории существует некое деление задач по видам деятельности учащихся. Это необходимо для нашего подхода к оценке их уровня качества. Опишем каждый вид.

1. Продуктивные задачи.

Данный тип задач, как видно из названия, учитывает творческую деятельность учащихся, то есть при решении таких задач необходимо провести маленькое исследование или поставить небольшой мысленный эксперимент. Это необходимо для полного и верного решения. К такому типу задач относят, например, качественные задачи. Естественно, что данный тип задач является достаточно сложным для решения, и поэтому часто используется на олимпиадах.

Рис. 1. Пример продуктивной задачи.

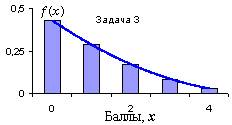
Рис. 2. Распределение по баллам для этой задачи.

2. Репродуктивные задачи.

Этот тип задач дает возможность учитывать репродуктивную деятельность учащихся. При решении задач такого типа необходимо либо знать определенную формулу, либо вспомнить ее. По сути, данные задачи тАУ это просто набор определенных формул, связанных общими неизвестными (найдем данную величину из этой формулы, подставим вот в эту и получим искомый результат). Такие задачи обычно очень легкие, буквально в одно действие. Из-за их простоты, достойного применения на олимпиадах они не нашли. Однако, как потом выяснится, зря. К такому типу задач можно отнести задачи учебника на повторение (особенно, 11 класс Мякишева), а также большая часть задач из сборника Рымкевича.

Рис. 3. Пример репродуктивной задачи.

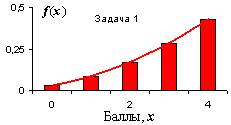
Рис.4. Распределение для этой задачи.

3. Продуктивно-репродуктивные задачи.

Это тАУ самый интересный тип задач. Он представляет собой смесь первых двух видов, что делает его привлекательным для большинства составителей олимпиадных заданий. В принципе, это верно, ведь данный тип позволяет проверить знания учащихся сразу в нескольких аспектах. Задачи такого типа, очевидно, могут иметь различную структуру (см. рис. 5 и рис. 6). На рисунке ниже представлено два интересных варианта такой структуры.

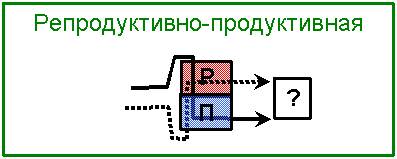
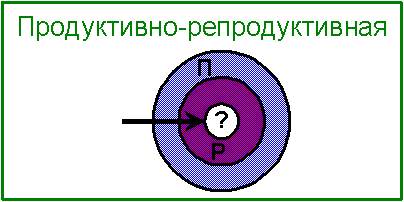
Рис. 5. Две структуры продуктивно-репродуктивных задач.

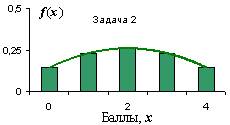
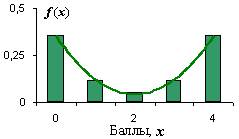
Рис. 6. Распределения для этих задач.

Ход решения таких задач во многом зависит от их подвида. Например, задача типа Влдодуматься, а потом вспомнитьВ» относится как раз к этому классу. Ясно, что задачи такого типа получили наибольшее распространение на олимпиадах, а также в задачниках для поступающих в ВУЗы.

Вз4. Понятие о сбалансированном комплекте олимпиадных заданий. Шкала сложности.

Введение данного понятия необходимо по нескольким причинам: первая причина заключается в том, что для построения такой педагогической модели, которую мы используем в данной работе, необходим какой-то определенный идеализированный подход к олимпиадным заданиям. То есть нужно представить себе идеальный случай, при помощи которого можно описать (математически и, главное, педагогически) все реально встречающиеся варианты. Вторая причина состоит в том, что для построения шкалы сложности задач, нужно иметь какой-то базовый элемент, относительно которого и происходит построение этой шкалы.

В данном параграфе описывается лишь формальное введение основного понятия данной теории. В полном описании математического вывода и доказательства педагогической оправданности сбалансированного комплекта задач нет необходимости в силу того, что сама по себе автоматизированная система не использует этого понятия, а использует только математические выводы, которые сделаны на его основе.

Под сбалансированным комплектом олимпиадных заданий, в контексте данной работы, будем понимать такой комплект заданий, в котором максимально равномерно воссоединены жесткий, естественный и щадящий режимы испытания для вывода серии всех испытаний школьников на гуманное отношение к личности школьников и бережное отношение к их талантам. В рамках представлений обсуждаемой модели, исходят из двух видов учебной деятельности учащихся и объясняют разный уровень сложности задач разным насыщением их решений формальными и творческими моментами. Эти требования к комплекту тождественны требованиям сбалансированности и полноты этого комплекта по отношению к репродуктивному, продуктивно-репродуктивному и продуктивному видам деятельности учащихся.

Хочется обратить внимание на то, что сбалансированный комплект представляет собой лишь идеализированную модель педагогического испытания школьников на олимпиадах. Ясно, что такой комплект в реальных условиях подобрать крайне сложно, однако он позволяет судить о том, какими должны быть олимпиадные задания, чтобы, в результате, можно было максимально приблизится к идеалу.

Вопрос об уровне сложности задач носит в рамках рассматриваемой теории достаточно важный характер. Наиболее исчерпывающий ответ на него может дать шкала сложности задач. Основные особенности подобной шкалы непосредственно оговариваются в исходных положениях теории. В связи с этим, следует упомянуть два момента. Первый момент заключается в том, что для полного анализа задач достаточен учет двух различных и несводимых друг к другу видов учебно-познавательной деятельности школьника тАУ репродуктивной и продуктивной. Второй момент изначально оговаривает большие способности каждого школьника к репродуктивному виду деятельности по сравнению с продуктивным. Этот момент условно выразим неравенством: .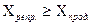

Принципиальная особенность указанных моментов заключается в том, что они определяют заведомо двумерный характер шкалы сложности задач. На этой шкале каждая задача должна характеризоваться двумя индексами, учитывающими два вида деятельности учащихся. В соответствии с этим любой единый показатель уровня сложности задач должен быть двумерным объектом. Это касается всех возможных шкал, включая и простейший случай ранжированной шкалы, оперирующей лишь целочисленной нумерацией уровней сложности задач. Она должна быть также двойной. Из всего сказанного выше ясно, что каждая задача в комплекте характеризуется точкой с координатами (k_n,k_p) на шкале. Где k_n тАУ индекс задачи, характеризующий продуктивный (творческие задачи) вид деятельности, а k_p тАУ индекс, характеризующий репродуктивный (типовые задачи) вид деятельности.

Кроме всего прочего, для построения шкалы сложности особую значимость имеет местоположение на ней двух задач тАУ ВлочевиднойВ» и ВлнедоступнойВ», ограничивающих весь возможный диапозон сложности задач. ВлОчевиднуюВ» задачу можно определить как задачу, которую полностью решают все участники без исключения. В решении ВлнедоступнойВ» задачи ни один из участников не способен сделать даже одного оцениваемого шага.

Возможен еще один интересный вариант задачи. Такую задачу условно назовем ВлнулевойВ». Она соответствует равновероятному распределению участников по набираемым баллам. ВлНулевуюВ» задачу можно одновременно считать как творческой, так и типовой.

Сама шкала сложности, согласно теории, имеет вид, представленный на рис. 1:

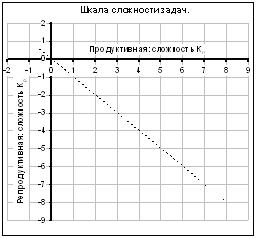
Рис. 1. Вид шкалы сложности.

Крайне интересным представляется расположение на этой шкале ВлочевиднойВ», ВлнедоступнойВ» и ВлнулевойВ» задач. Очевидно, исходя из определения задач, видно, что ВлочевиднаяВ» задача тАУ это есть предельный

Вместе с этим смотрят:

Methods of teaching speech

Modern technologies in teaching FLT

University of Cambridge

WEB-дизайн: Flash технологии

РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському