Гуманитаризация обучения математике
Ничем не оправданное выхолащивание нашей школы на протяжении многих лет привело к резкому снижению уровня общей культуры и воспитанности выпускников школ и, следовательно, общества в целом. В век научно-технической революции мы на каждом шагу сталкиваемся с вопиющей неграмотностью и отсутствием вкуса, неумением людей использовать программные школьные навыки на практике.
Поэтому основным направлением развития школы сегодня является поворот обучения к человеку. Школьный курс содержит довольно сложные предметы, такие как математика, физика, химия и другие, которые не всем даются легко, и как следствие этого - потеря интереса к обучению.
Не все дети одарённые в математическом смысле. Конечно знания, умения и навыки, безусловно, нужны, но в меру. Для особо способных детей существуют специальные программы, имеются факультативы, кружки, но речь сейчас не о них. Путей достижения психологической комфортности в обучении математики существует немало. Наиболее актуальным на данный момент является внедрения технологий гуманитаризации в обучение математики. Ведь гуманитаризация предполагает усиление взаимосвязи естественно-математического образования с гуманитарным, т.е. более понятным, близким ребёнку, усиление практического и прикладного аспектов в её преподавании. Это означает, что в обучении математике акцент необходимо ставить на общее развитие учащегося, а именно на развитие логического мышления, математической речи, пространственного воображения, интуиции, чувства прекрасного.
Предметом исследований данной работы мы избрали технологию гуманитаризации.
В последнее время очень многие исследователи работают над выявлением гуманитарного потенциала математики как науки (Л.П. Бестужева, Н.Н. Костин, Е.С. Петрова, Т.А. Корешкова, Н.Ф. Усынина, А.Н Чалов и др.), отдавая предпочтение либо истории, либо художественной литературе, либо поэзии, либо философии, т.е. различным составляющим общей культуры.
Так А.В. Дорофеева обосновывает тезис о том, Влчто история математики помогает формированию мировозрения учащихсяВ». Причем, по её мнению, Влэлементы истории математики привлекают школьников, склонных к гуманитарным наукамВ» и отстающих учащихся. На сегодняшний день, данный тезис представляется актуальным с точки зрения привлечения внимания школьников различных способностей и интересов к математике как науке.
Исследования К.В. Лавринович охватывают не только историю, но и другие области человеческого познания. Так исследователь раскрывает необходимость Влвключения Влдругих искусств»» в содержание математического образования. Под термином Влдругие искусстваВ» понимается использование поэзии, истории, картин известных художников и т.п. на уроках математики.
В. Гачев считает, что познание целого невозможно без познания частей, поэтому негуманитарные и гуманитарные науки следует не просто рассматривать в контексте культуры, важно отыскивать взаимосвязи Влмежду двумя колоссальными, самостоятельными системами внутри культуры, т.е. осуществлять привод и перевод математики, её проблем, задач, языка тАУ на сюжеты гуманитарной культуры, на язык её образов, символов, мифов, категорийВ».
Опираясь на выше изложенное, в нашей работе мы представим некоторые рекомендации по применению технологии гуманитаризации при изучении темы ВлДробные числаВ» в 5-6 кл.
Для реализации этой цели поставлены задачи:
1. Раскрыть технологию гуманитаризации и ее основные положения.
2. Охарактеризовать гуманитарный потенциал современных учебников для 5-6 классов.
3. Разработать рекомендации использования технологии гуманитаризации при изучении дробей.
Надеемся, что проведённые в работе исследования послужат практическим приложением для учителей математики.
Глава I ВлТехнология гуманитаризацииВ»
1.2 Понятие педагогической технологии
Необходимость разработки технологии гуманитаризации школьного математического образования вызвана актуальностью проблемы на современном этапе реформирования школьного образования. Но, к сожалению, лишь немногие педагоги и методисты (В.В. Гузеев, Т.А. Иванова, К.В. Лавринович, Л.Ф. Пичурин и др.) видят пути решения указанной проблемы, предлагая учителям-практикам методические разработки или учебные пособия, раскрывающие возможности гуманитаризации школьного математического образования, развивать педагогические технологии, необходимые для этого.
Что же понимается под Влпедагогической технологиейВ». Существуют различные к определению этого понятия: В.П. Беспалько, И.П. Волков, М.В. Кларин, В.М. Монахов Н.В. Чекалев и др. Так В.М. Монахов представляет педагогическую технологию, как продуманную модель совместной педагогической деятельности по проектированию, организации и проведению учебного процесса с обеспечением комфортных условий для учащихся и учителя.
С позиции системного подхода анализирует понятия Влпедагогическая технологияВ» М.В. Кларин, рассматривая его как системную совокупность и порядок функционирования всех личностных, инструментальных и методических средств, используемых для достижения педагогических целей.
В соответствии с теорией педагогических технологий В.П. Беспалько определения терминов Влпедагогическая технологияВ» и Влпедагогическая системаВ» следующие: ВлПедагогическая технология тАУ это проект определённой педагогической системы, реализуемый на практике. Педагогическая система тАУ это определенная совокупность взаимосвязанных средств, методов и процессов, необходимых для создания организованного, целенаправленного педагогического влияния на формирование личности с заданными качествамиВ».
Структура любой педагогической системы, по мнению В.П. Беспалько, представляется следующей взаимосвязанной совокупностью инвариантных элементов: 1 - учащиеся; 2 - цели обучения; 3 тАУ содержание обучения; 4 тАУ дидактические процессы; 5 тАУ учитель, технические средства обучения, наглядные средства обучения; 6 тАУ организационные формы обучения. Причем первые три из перечисленных элементов представляют собой дидактическую задачу, а последующие тАУ непосредственно педагогическую технологию.
На наш взгляд наиболее удачный подход к понятию Влпедагогическая технологияВ» представлен в исследованиях Г.К. Селевко. Автор обобщает и систематизирует все имеющиеся на сегодняшний день технологии обучения, раскрывает взаимосвязь между ними, выделяет структурные компоненты образовательных технологи, классифицирует их.
Согласно теории Г.К. Селевко понятие Влпедагогическая технологияВ» представимо тремя аспектами:
Вл1) научным: педагогические технологии тАУ часть педагогической науки, изучающая и разрабатывающая цели, содержание и методы обучения и проектирующая педагогические процессы;
2) процессуально-описательным: описание процесса, совокупность целей, содержания, методов и средств для достижения планируемых результатов обучения;
3) процесуально-деятельностным: осуществление технологического процесса, функционирование всех личностных, инструментальных и методических педагогических средствВ».
Именно последний подход лежит в основе технологии гуманитаризации школьного математического образования.
Основываясь на исследованиях И.Д. Пехлецкого, введём понятийный аппарат, необходимый для раскрытия технологии гуманитаризации школьного математического образования.
Математические объекты тАУ Влвсе математические понятия, имеющие самостоятельный смысл и употреблениеВ». Утверждения о математических объектах и их свойствах, различные связи между объектами и утверждениями будем называть логическими конструкциями.
Гуманитарные объекты представляют собой элементы различных систем гуманитарной культуры тАУ истории, музыки, искусства, архитектуры, скульптуры, различных жанров литературы и т.д.
Изучение математических объектов и логических конструкций происходит на когнитивном уровне; изучение же гуманитарных объектов тАУ преимущественно на эмоционально- ценностном, чувственном уровне.
Составные объекты тАУ органически взаимосвязанные между собой математические объекты, логические конструкции и гуманитарные объекты. Взаимосвязи между перечисленными объектами и конструкциями осуществляются в большей степени на эмоционально-ценностном уровне, хотя и без участия когнитивных процессов.
При описании технологии гуманитаризации школьного математического образования будем использовать следующие структурные компоненты:
1. Общая характеристика технологии гуманитаризации школьного математического образования, её цели и основные принципы.
2. Дидактические усовершенствование и реконструирование содержания математического образования при реализации технологии гуманитаризации.
3. Деятельностное и программно-методическое обеспечение технологии школьного математического образования.
1.2. Основные положения теории гуманитаризации
Название технологии: технология гуманитаризации школьного математического образования. Данное название отражает характер основных направлений модернизации системы обучения.
Идентификация:
- по уровню применения данная технология обучения является частно-предметной, так как раскрывает особенности обучения математике;
- по отношению к ребёнку тАУ личностно-ориентированная;
- по направлению модернизации традиционной системы обучения данная технология основывается на конкретной реализации идеи гуманитаризации школьного математического образования, раскрытой ранее.
Концептуальная часть:
Позиция ребёнка. Рассмотрим законы высшей нервной деятельности, объясняющие процессы познания. Первый закон взаимной индукции. Суть его в следующем: Влесли возбуждаются одни участки головного мозга, то в других в это время идут процессы торможенияВ». Например, когда решается математическая задача, все знания о литературе, театре как бы ВлзамираютВ». Второй закон тАУ закон динамического стереотипа: Влпри частых, постоянных раздражениях одних участков головного мозга и столь же постоянных раздражениях других происходит устойчивое распределение очагов возбуждения. М.Л. Портнов подмечает важную закономерность: Влчем больше очагов возбуждения, тем больше их может появиться тАУ возможности головного мозга во много раз выше, чем кажетсяВ».
Описанные характеристики познавательного процесса дают возможность предположить, что обучение учащихся будет носить более продуктивный характер, если при изучении дисциплин естественно-математического цикла мы по возможности будем множественно воздействовать на различные участки головного мозга, используя органические гуманитарных и негуманитарных дисциплин.
Сформулируем цели положенные в основу технологии гуманитаризации школьного математического образования.
Учебные цели в когнитивной области:
- формировать умения учащихся строить новые сочетания математических знаний со знаниями, полученными из системы гуманитарной культуры;
- формировать умения учащихся транслировать математический материал из одной формы выражения в другую, т.е. умение интерпретировать учеником математический материал с помощью гуманитарных объектов;
- формировать умения учащихся использовать изученный математический и гуманитарный материал в конкретных условиях и новых ситуациях, отыскивать точки соприкосновения математической и гуманитарной культур.
Заметим, что, сформулированные выше цели не касаются теоретических основ математики, поскольку задача предлагаемой технологии гуманитаризации тАУ не вносить изменения в действующую систему математических знаний, а обогащать её гуманитарными объектами.
Учебные цели в эмоционально-ценностной области:
- формировать восприятие учащимися целостной картины мира, а не разделённой на различные области человеческого познания;
- формировать эмоционально-личностное отношение учащихся к таким составным частям культуры, как математика и гуманитарные науки;
- способствовать концептуализации ценностных ориентаций учащихся к составным частям культуры, организации собственной системы ценностей. Это предполагает, что в результате реализации технологии ученик имеет не просто определенные знания, принадлежащие к различным системам культуры, но и свободно ориентируется в категориях этих систем, имеет собственное мнение, объективно оценивает свои возможности и Влстроить жизненные планы в соответствии с осознанием им самим собственных способностей, интересов и убежденийВ»;
- развивать правополушарные и левополушарные возможности учащихся как одного из условий формирования необходимого уровня Влусвоения ценностей, на котором они устойчиво определяют поведение индивида, входят в привычный образ действий, входят в привычный образ действий, или жизненный стильВ».
Учебные цели в психомоторной области сводятся в основном к формированию единой речевой культуры. Заметим, что мы не формируем навыки, а несколько углубляем их, формируя определенные качества речи, т.е. ее содержательность, доступность, логичность, выразительность, действенность.
1.3. Принципы, положенные в основу технологии гуманитаризации школьного математического образования
При построении технологии гуманитаризации школьного математического образования осуществляется системный подход. Элементами этой системы являются цели, содержание школьного математического образования, раскрывающее связи с предметами гуманитарного цикла, законы высшей нервной деятельности, объясняющие процессы познания, методы и средства обучения. Фунционирование указанных элементов системы должно основываться на следующих основополагающих принципах: принципах гуманизации; принцип личностно-ориентированного подхода; принцип целостности; принцип выделения основной структуры системы; принцип органичности.
Остановимся подробнее на принципах, положенных в основу технологии школьного математического образования, подчеркивая еще раз, что эти принципы должны представлять технологию как педагогическую систему с необходимым перечнем принципов, присущих системному подходу.
Принцип целостности
Этот принцип является одним из наиболее важных. Это означает, что при разработке педагогической системы необходимо добиваться гармонического взаимодействия всех компонентов педагогической системы как по горизонтали (в рамках одного периода обучения тАУ четверти, учебного года), так и по вертикали тАУ на весь период обучения.
Принцип выделения основной структуры системы
Важность данного принципа обосновывается в теории систем И.Д. Пехлецкого. Исследователь считает, что это один из основных принципов, которые должен Влналожить свой отпечаток на все фундаментальные определения и понятия теории системыВ». Причем смысл принципа выделения основной структуры системы состоит в том, что Влвсякое научное рассмотрение, анализ или моделирование достаточно сложной, абстрактной или реальной системы не возможны без процесса выдвижения на первый план некой части структуры системы.
Конкретизируя все сказанное на примере технологии гуманитаризации школьного математического образования, т.е. конкретной педагогической системы. С позиций целей исследования основной частью такой педагогической системы будет являться математическое содержание. Ко всей же остальной структуре педагогической системы относятся гуманитарные и составные объекты.
Принцип органичности
Принцип органичности означает, что при разработке технологии гуманитаризации школьного математического образования необходимо достичь органичного взаимодействия между математическими и гуманитарными системами культуры. Гуманитарные объекты должны естественным образом включаться в математическое содержание. Этот принцип должен найти отражение, при создании составных объектов, а также всеми компонентами технологии гуманитаризации.
Технология гуманитаризации
школьного математического образования
| ОСНОВНЫЕ КОМПОНЕНТЫ |
Концептуальный В· позиция ребёнка: множественное воздействие на различные участки головного мозга; В· учебные цели в когнитивной, эмоционально-ценностной, психомоторной областях; В· принципы: выделения основной структуры системы; целостности; органичности. | Содержательный В· математические объекты и логические конструкции; В· гуманитарные и составные объекты. | Деятельностный В· конкретизируются методики формирования мотивации учащимися; В· характеризуются четыре стадии учебно-познавательной деятельности учащихся: репродуктивная, алгоритмическая, эвристическая и творческая. |
Программно-методическое обеспечение: В· использование различных видов уроков: от классического до нетрадиционного; В· гуманитаризированные учебники, учебно-методическая литература и др. |
Глава II ВлПрактическое применение
элементов технологии гуманитаризацииВ»
2.1 Анализ программы
Изучение программного материала по теме ВлДробные числаВ» дает возможность учащимся:
- овладеть достаточно развитой техникой вычислений с рациональными числами; овладеть навыками устных вычислений;
- овладеть первоначальными навыками работы с приближенными значениями;
- усовершенствовать умения решать, в том числе текстовые задачи на дроби, проценты;
- ознакомить с некоторыми историческими сведениями о возникновении и развитии чисел.
Уровень обязательной подготовки определяется следующими требованиями:
- знать и правильно употреблять термины, связанные с дробными числами: дробное, обыкновенная дробь, десятичная дробь; уметь переходить от одной формы записи чисел к другой;
- уметь сравнивать дробные числа;
- уметь изображать дробные числа на координатной прямой и определять координату точки;
- уметь выполнять сложение, вычитание, умножение, деление, возведение в квадрат и куб обыкновенные и десятичные дроби; приобрести навыки устных вычислений; уметь находить значение числовых выражений;
- округлять десятичные дроби;
- решать основные задачи на дроби и проценты.
На изучение темы ВлДробные числаВ» программой отводится в общем 64 ч в 5 кл. и 58 ч в 6 кл. За это время учащиеся должны овладеть всеми знаниями и умениями, представленными выше. Однако, помимо знаний обязательного материала они могут получить и дополнительный материал, представленный информацией из области других предметов: истории, литературы, географии и др.
2.2 Особенности содержания и структуры курса
Для всего курса характерны опора на здравый смысл и интуицию, развития умения применять математику в реальной жизни, знакомство с математикой как частью общечеловеческой культуры. Содержание курса развивается тАЬпо спиралитАЭ, что позволяет неоднократно возвращаться к знакомому материалу на новом уровне, формировать системные знания; при этом последовательно реализуется принцип тАЬразделения трудностейтАЭ.
В 5-6 классах усилено внимание к арифметике и арифметическим (т.е. логическим) методам решения задач. Существенно повышена роль геометрического материала: здесь представлена наглядная геометрия, направленная на развитие образного мышления, пространственного воображения, изобразительных умений.
Методический аппарат учебников. Учебники включают в себя как объяснительный текст, так и богатую систему упражнений, распределенных по уровню сложности в группы А и Б. В систему упражнений включаются советы, указания, образцы решений, интересные для учащихся формы заданий тАУ задания с выбором ответа, задачи-исследования.
Во всех книгах присутствует рубрика ВлДля тех, кому интересноВ» - это обязательный материал, позволяющий расширить и углубить знания учащихся. Каждую главу завершает рубрика ВлЗадания для самопроверкиВ», в которой представлены обязательные результаты обучения.
Рассмотрим и проанализируем содержание и оформление основных учебников используемых в настоящее время в работе учителями школ.
Большинство учителей используют учебники: Нурка Э. П. (А. Е. Тельгмаа), Виленкина ( Чеснокова, Шварцбурга, Жокова).
Выясним основные содержания этих учебников:
| Нурк | Виленкин |
| 5 класс |
1. Нат. числа, Вл+В» и тАЬ-тАЬ 2. ВлxВ» и Вл:В» нат. Чисел 3. Углы, треугольники и прямоугольники. 4. Дробные числа, сложение и вычитание десятичных дробей. 5. ВлxВ» и Вл:В» десятичных дробей. | 1. Натуральные числа. 2. Дробные числа. |
| 6 класс |
1. Делимость нат. чисел. 2. Обыкновенные дроби, Вл+В» и Вл-В» 3. ВлxВ» дробей. 4. Вл:В» дробей, пропорции. 5. Положительные и отрицательные числа, система координат. 6. Действия с рациональными числами. | 1. Обыкновенные дроби. 2. Рациональные числа. |
Рассмотрим особенности приведенных учебников и сравним их содержание.
Система управлений и заданий:
1. Нурк содержит два уровня:
А тАУ низкий, В тАУ выше, * - нестандартные задания. Присутствуют задания на повторение. В конце учебника тАУ курс повторения по всем темам этого учебника и задачи для любителей математики. Система упражнений разнообразная и разноуровневая.
Также в учебнике есть справочный материал: на обложках формулы площадей прямоугольника и квадрата; объема прямоугольника, параллелограмма, куба; сложение и вычитание обыкновенных дробей; проценты; математический алфавит, таблица простых чисел.
К каждой теме автором подобран исторический материал, даны темы рефератов, указаны источники.
2) Виленкин. Содержит: / - правила, ? тАУ вопросы к упражнениям, К тАУ упражнения для работы в классе, П тАУ повторение, Д тАУ домашние задания, @ - исторический материал, Г тАУ упражнения для правильного говорения, М тАУ нестандартные задания. Есть также ответы на задания. Набор упражнений очень большой.
Присутствует дополнительный материал в виде: латинского алфавита, формул объемов и площадей, и метрических соотношений, таблица простых чисел. Исторический материал.
Т. О. Можно сделать вывод по основам рассмотрим выше: самое удачное оформление у учебников Нурка и Виленкина; набор разноуровневых заданий тАУ Нурк; удобен в работе для родителей тАУ Нурк; теория лучше дана у Нурка и Виленкина.
Исторический материал приведен в достаточном количестве только у Виленкина, но содержится также и у Нурка.
Отдельно хотелось бы рассмотреть содержание учебников Дорофеева, внедряемых в практику с 1995 года. Для всего курса характерны опора на здравый смысл и интуицию, развитие умения применять математику в реальной жизни, знакомство с математикой как частью общественной культуры. Содержание курса развивается Влпо спиралиВ», что позволяет неоднократно возвращаться к знакомому материалу на новом уровне, формировать системные знание; при этом последовательно реализуется принцип Влразделение трудностейВ».
В 5-6 классах усилено внимание к арифметике и арифметическим методам решения задач. Существенно повышена роль геометрического материала: здесь представлена наглядная геометрия, направленная на развитие образного мышления, пространственного воображения, изобразительных умений.
В учебниках последовательно вводиться новая для нашей школы содержательно-методическая линия ВлАнализ данныхВ», включающая комбинаторику, элементы теории вероятностей и статистику. Эта линия органично сочетается с традиционными вопросами курса и существенно усиливает его практическое и прикладное звучание.
Принятые при построении курса методические подходы направлены на то, чтобы обеспечить понимание и осознанность при изучении материала, облегчить учащимся запоминание информации, сформировать у них системные знания, помочь овладеть набором разнообразных стратегий решения задач. К ним относятся:
- приоритет развивающей функции обучения, это меняет акценты в преподавании, явно выдвигает задачу формирования интеллектуальной восприимчивости, гибкости, независимости мышления;
- внимание к мотивационной стороне обучения, что способствует активизации познавательной деятельности, повышению интереса к изучаемому материалу;
- организация этапа содержательно-практической деятельности как исходного при введении новых понятий позволяет создать у учащихся запас содержательных представлений, служащих основой для последующей формализации, способствует лучшему пониманию, даёт возможность школьникам открывать новые знания;
- целенаправленное обучение приёмам и способам рассуждений, обогащающее интеллектуальный багаж школьников и эффективно развивающее их мышление;
- реализация идеи уровневой дифференциации, что позволяет работать с учащимися разного уровня подготовки и способностей, выстраивать индивидуальные траектории обучения;
- личностно-ориентированный стиль изложения, который выражается в живом и эмоциональном языке, широком использовании диалога и обращений к ученику, привлечении совместных сюжетов при изложении теории и в задачном материале.
Учебники включают в себя как объяснительный текст, так и богатую систему упражнений, распределённых по уровням сложности в группы А и Б. В систему упражнений включаются советы, указания, образцы решения, интересные для учащихся формы заданий тАФ задания с выбором ответа, задачи-исследования.
Во всех книгах присутствует рубрика ВлДля тех кому интересноВ» тАФ это необязательный материал, позволяющий расширить и углубить знания учащихся. Каждую главу завершает рубрика ВлЗадания для самопроверкиВ», в которой представлены обязательные результаты обучения.
Рассмотрев все эти учебники можно сделать вывод, что в работе желательно использовать учебники Виленкина и Дорофеева (возможно их параллельное применение).
2.3 Методика изучения дробных чисел
В практике преподавания основным методом изучения дробных чисел являются поясняющие описания, которые опираются на жизненный опыт и знания учащихся. Поясняющие описания не заменяют определений, понятий, а лишь показывают целесообразность их введения.
Введение дробных чисел в школьном курсе связывается с необходимостью более точного измерения величин, с делением чисел. В связи с этим целесообразно познакомить учащихся с возникновением дробных чисел в процессе практической деятельности человека, а именно в процессе измерения. Краткая историческая справка поможет учащимся лучше овладеть данным материалом. Содержание её может быть примерно следующим.
Измерение, так же как и счет, имело место у всех народов с самых древних времён; измерение было непосредственно связано со счетом. Потребность в более точном измерении явилась причиной того, что единицы мер стали раздроблять на две, на три и более частей. Этим более мелким мерам давали особые наименования, и в дальнейшем величины измерялись уже этими более мелкими единицами, однородными с ними. Так возникли первые конкретные дроби. Отвлеченных дробей в это время еще не знали.
Длинен был путь перенесения названия какой-либо части одной меры на такую же часть другой меры, это был путь создания абстрактного понятия дроби.
Так, например, в России была земельная мера четверть и более мелкая тАУ получетверть, которая называлась осьмина. Это были конкретные дроби, единицы для измерения площади земли, но осьминой нельзя было измерить время или скорость и др. Значительно позднее осьмина стала означать отвлеченную дробь 1/8, которой можно выразить любую величину. Дроби первоначально в русских рукописях назывались долями, затем ломаными числами. При записи числа использовалась горизонтальная черта.
Довольно долгим был путь и к введению десятичных дробей. В древности некоторые народы пользовались шестидесятеричной системой счисления и дроби записывались в шестидесятеричной системе так же, как в настоящее время записывают наши десятичные дроби. Римляне пользовались двенадцатеричными дробями.
В 16 тАУ 17 вв. в связи с развитием общества, с развитием науки и техники возникла необходимость облегчить громоздкие вычисления. Внимание математиков было обращено к десятичным дробям, к десятичной системе мер. В России учение о десятичных дробях впервые было изложено в ВлАрифметикеВ» Магницкого, где были приведены и десятичные меры длины и площади. В этой же работе излагается и учение о шестидесятеричных дробях (отголосок вавилонской шестидесятеричной системы счисления).
Учащимся нужно также показать, что дроби применяются не только в математике, но и, например, в музыке.
Все знают, что Пифагор был учёным и, в частности, автором знаменитой теоремы. А то, что он был еще и блестящим музыкантом, известно не так широко. Сочетание этих дарований позволило ему первым догадаться о существовании природного звукоряда. Надо было ещё доказать это. Пифагор построил для своих экспериментов полуинструмент-полуприбор тАФ ВлмонохордВ». Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы удобнее было зрительно делить струну на части. Множество опытов проделал Пифагор с монохордом и, в конце концов, описал математически поведение звучащей струны. Работы Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой.
Оказывается, для музыки семь звуков внутри октавы такая же естественная вещь, как десять пальцев на руках в арифметике. Уже тетива самого первого лука, колеблясь после выстрела, давала готовым тот набор музыкальных звуков, которыми мы почти без изменения пользуемся до сих пор.
С точки зрения физики тетива и струна тАФ одно и то же. Да и сделал человек струну, обратив внимание на свойства тетивы. Звучащая струна колеблется не только целиком, но одновременно и половинками, третями, четвертями и т.д. Подойдём теперь к этому явлению с арифметической стороны. Половинки колеблются вдвое чаще, чем целая струна, трети тАФ втрое, четверти тАФ вчетверо. Словом, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота её колебаний. Допустим, вся струна колеблется с частотой 24 герца. Высчитывая колебания долей вплоть до шестнадцатых, мы получим ряд чисел, показанных в таблице. Эта последовательность частот так и называется тАФ натуральный, т.е. природный, звукоряд.
| 1 | 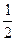
| 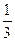
| 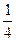
| 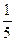
| 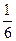
| 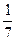
| 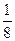
| 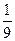
| 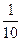
| 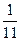
| 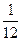
| 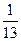
| 
| 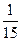
| 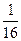
|
| 24 | 48 | 72 | 96 | 120 | 144 | 168 | 192 | 216 | 240 | 264 | 288 | 321 | 336 | 360 | 384 |
Согласно программе и учебнику по математике формирование понятий дроби начинается с умения получать доли при делении какой-либо величины на несколько равных частей.
Учащимся предлагается разделить на равные части знакомые предметы, такие, как арбуз, дыня, пирог и др., и выделить одну из частей, одну из долей. Такие же по характеру упражнения выполняют учащиеся с использованием геометрического материала: деление отрезка, круга, квадрата на равные части, на равные доли и взятие одной такой части, одной доли. От выделения одной части и взятию нескольких таких частей.
Учащимся сообщается, что для выражения одной или нескольких долей предмета нужны новые числа, а именно дроби. Далее приводятся примеры обыкновенных дробей и даётся форма записи обыкновенной дроби, проводится обучение чтению. Учащиеся должны помнить: числитель дроби тАФ количественное числительное женского рода (одна, две и т.д.), а знаменатель тАФ порядковое числительное (седьмая, сотая, двести тридцатая и т.д.).
Например, 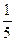 тАФ одна пятая;
тАФ одна пятая; 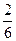 тАФ две шестых;
тАФ две шестых; 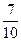 тАФ семь десятых;
тАФ семь десятых;
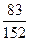 тАФ восемьдесят три сто пятьдесят вторых. В процессе работы над закреплением понятия дроби необходимо познакомить учащихся с происхождением слова ВлдробьВ», ввести термины ВлчислительВ», ВлзнаменательВ». Это можно сделать следующим образом.
тАФ восемьдесят три сто пятьдесят вторых. В процессе работы над закреплением понятия дроби необходимо познакомить учащихся с происхождением слова ВлдробьВ», ввести термины ВлчислительВ», ВлзнаменательВ». Это можно сделать следующим образом.
В начале урока учащимся можно предложить три ребуса: