Анализ методов прогнозирования
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ЗАПОРОЖСКИЙ ГОСУДАРСТВЕННЫЙЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА МЕЖДУНАРОДНЫХ ЭКОНОМИЧЕСКИХ ОТНОШЕНИЙ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ ПО ДИiИПЛИНЕ ВлМеждународная информацияВ»
Анализ методов прогнозирования
Разработал:
.
Руководитель:
Реферат
Пояснительная записка: 28 страниц, 7 рисунков, 1 формула, 9 источников
Объект исследования: методы прогнозирования.
Цель работы: изучить методы прогнозирования и провести их анализ
Методы исследования: дедукция, системно-структурный
Результаты исследования: в процессе работы был проведён анализ методов прогнозирования, были рассмотрены некоторые теоретические аспекты определённых методов, сфера применения методов прогнозирования, и на конкретном примере был представлен метод экстраполяции и тенденции.
Ключевые слова : прогнозирование, экстраполяция, экспертные методы, эвристика, информация, технология, обработка информации
Содержание
ВведениетАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.6
1. Задачи и принципы прогнозированиятАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж7
2. Методы научно-технического прогнозирования тАжтАжтАжтАжтАжтАжтАжтАжтАж11
2.1 Классификация методов прогнозированиятАжтАжтАж.тАжтАжтАжтАжтАжтАжтАж.11
2.2 Экстраполяционные методы прогнозированиятАжтАжтАжтАжтАжтАжтАжтАжтАж.13
2.2.1 Предварительная обработка исходной информации в задачах прогнозной экстраполяциитАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж14
2.3 Статистические методытАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж16
2.4 Экспертные методытАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж17
2.4.1 Область применения экспертных методовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж17
2.4.2 Метод эвристического прогнозирования (МЭП)тАжтАжтАжтАжтАжтАжтАж.19
3. Классификация экономических прогнозовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.23
ВыводтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.28
Перечень ссылоктАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж29
Перечень сокращений
ТЭО тАУ таблица экспертных оценок
ПЭО тАУ персональная экспертная оценка
МЭП тАУ метод эвристического прогнозирования
ЭВМ тАУ электронно-вычислительная машина
ЭЦВМ тАУ электронная центральная вычислительная машина
МГД тАУ магнитно-динамические установки
НТИ тАУ научно-техническая информация
ВВЕДЕНИЕ
Процесс прогнозирования достаточно актуален в настоящее время. Широка сфера его применения. Прогнозирование широко используется в экономике, а именно в управлении. В менеджменте понятие ВлпланированиеВ» и ВлпрогнозированиеВ» тесно переплетены. Они не идентичны и не подменяют друг друга. Планы и прогнозы различаются между собой временными границами, степенью детализации содержащихся в них показателей, степенью точности и вероятности их достижения, адресностью и, наконец, правовой основой. Прогнозы, как правило, носят индикативный характер, а планы обладают силой директивного характера. Не подмена и противопоставление плана и прогноза, а их правильное сочетание тАУ таков путь планомерного регулирования экономики в условиях рыночной экономики и перехода к ней.
В промышленности методы прогнозирования также играют первостепенную роль. Используя экстраполяцию и тенденцию, можно делать предварительные выводы относительно разных процессов, явлений, реакций, операций.
Определённую нишу прогнозирование занимает и в военных дисциплинах. Используя методы прогнозирования, можно определить(оценить) радиоактивную обстановку местности и т. д.
Существует много методов прогнозирования. Продифференцировав их общее число, необходимо выбрать оптимальный из них для использования в каждой конкретной ситуации.
Анализ методов прогнозирования, изучение этих методов, использование их в разных сферах деятельности является мероприятием рационализаторского характера. Степень достоверности прогнозов можно затем сравнить с действительно реальными показателями, и, сделав выводы, приступить к следующему прогнозу уже с существующими данными, т.е. имеющейся тенденцией. Опираясь на полученные данные, можно во временном аспекте переходить на более высокую ступень и т.д.
1. Задачи и принципы прогнозирования
Прогноз тАУ конкретное предсказание, суждение о состоянии какого-либо явления в будущем на основе специально научного исследования. Классификация прогнозов осуществляется, как правило, по двум признакам- временному и функциональному. По временному признаку различают прогнозы: кратко-, средне-, долгосрочные и сверхдолгосрочные. Функциональная классификация прогнозов предполагает их деление на исследовательские, программные и ресурсные.
Прогнозирование тАУ процесс разработки прогнозов. В зависимости от вида прогноза различают нормативное, поисковое, оперативное.
Прогнозная модель тАУ модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объектах в будущем и (или) путях и сроках их осуществления
Чтобы получить информацию о будущем, нужно изучить закоВнны развития народного хозяйства, определить причины, движущие силы его развития - это основная задача планирования и прогноВнзирования. В качестве основных движущих сил развития произВнводства выступают социальные потребности, технические возВнможности и экономическая целесообразность. В соответствии с этим можно указать на три основные задачи планирования и прогнозирования: установление целей развития хозяйства; изыскание оптимальных путей и средств их достижения; опредеВнление ресурсов, необходимых для достижения поставленных целей.
Выбор целей является результатом анализа социально-политиВнческих задач, которые необходимо решить в обществе и которые отображают объективный характер действия экономических законов.
Выбору целей предшествует разработка альтерВннатив целей, построение иерархической системы или Влдерева целейВ», ранжирование целей, выбор ведущих звеньев. Исходными предпосылками выбора целей являются, с одной стороны, реальВнная возможность решения данной альтернативы, а с другой - ее оптимальность по критерию эффективности.
Пути и средства достижения целей определяются на основе анализа развития народного хозяйства и научно-технического проВнгресса. При этом в. процессе прогнозирования происходит ограниВнчение области альтернативных вариантов путей и средств достиВнжения поставленных целей, т. е. определяется область оптимальВнных решений. В процессе разработки плана (принятия решения) определяется единственное решение, оптимальное по принятому вектору критериев.
В зависимости от того, какая задача решается в первую очеВнредь, различают два вида прогнозирования: исследовательское (или поисковое) и нормативное. Формирование прогноза объекВнтивно существующих тенденций развития на основе анализа исторических тенденций называется исследовательским или поисковым прогнозированием. Этот вид прогнозирования основан на использовании принципа инерционности развития, при котоВнром ориентация прогноза во времени происходит по схеме Влот настоящего тАФ к будущемуВ». Исследовательский прогноз тАФ это картина состояния объекта прогноза в определенный момент будущего, полученная в результате рассмотрения процесса развиВнтия как движения по инерции от настоящего времени до горизонВнта прогноза. Прогнозирование тенденций развития объекта проВнгноза, которые должны обеспечивать достижение в установленный момент будущего определенных социально-политических, эконоВнмических и оборонных целей, называется нормативным. В этом случае ориентация прогноза во времени происходит по схеме Влот будущего тАФ к настоящемуВ».
Рассогласование нормативных и исследовательских оценок объекта прогноза в каждый момент времени будущего является следствием противоречия ВлпотребноститАФвозможностиВ». КомпВнлексный прогноз строится на основе композиции исследовательВнского и нормативного прогнозов.
Выбор целей и средств для их достижения непременно должен сочетаться с определением потребности в ресурсах. При опредеВнлении этой потребности следует рассматривать плановые и проВнгнозные матрицы ресурсов (финансовых, трудовых, материальных и энергетических), а также матрицы производственных мощноВнстей и ресурсов времени. Оценке подлежат как потребные ресурВнсы, так и вероятные ограничения на их величину в диапазоне времени упреждения плана или прогноза. Матрицы ресурсов проВнгноза являются важнейшими исходными данными при составлеВннии балансов народного хозяйства при перспективном планироВнвании.
Движущие силы развития не действуют изолированно, они взаимосвязаны и взаимообусловлены и могут быть представлены в виде связного треугольника графа:
Рисунок 1.1 Взаимосвязь движущих сил развития
Вершины этого Влпричинного, треугольникаВ» идентифицируют движущие силы развития производства, его ребра тАФ обоюдные связи между ними. Поэтому задачи планирования и прогнозироВнвания нельзя рассматривать изолированно. В процессе прогнозиВнрования и разработки плана обязательно производится анализ взаимодействия целей, способов и технических средств их достиВнжения, ресурсов, необходимых для их реализации, и определяютВнся по принятым критериям эффективности оптимальные пути разВнвития народного хозяйства.
Несмотря на общность задач, их постановка при прогнозироВнвании и планировании различна. При планировании действует следующая схема: Влцель - директивная, пути и средства ее достиВнжения - детерминированные, ресурсытАФограниченныеВ». При проВнгнозировании схема иная: ВлцелитАФтеоретически достижимые, пути и средства их достижения - возможные, ресурсы - вероятныеВ». Задачи прогнозирования отличаются широтой охвата. Задачи прогнозирования надо оценивать как глоВнбальные. К ним можно отнести: анализ ситуации, определение уровней достоверности информации, определение степени вероятности, выработка текущих, средне- и долгосрочных прогнозов. Принципы прогнозирования: сочетание социальВнно-политических и хозяйственных целей; демократический центВнрализм; системность; непрерывность и обратная связь; пропорВнциональность и оптимальность; реальность и объективность; выделение ведущего звена и т. д.
Прогнозирование должно носить системный характер. Необходимость системного подхода в прогнозировании вытекает из особенностей развития науки и техники, народного хозяйства в период научно-технической революции. Научно-техническая ревоВнлюция привела к принципиальному изменению свойств, характеВнристик и структуры современной техники и народного хозяйства. Рост количества элементов, объектов различной природы, усложВннение связей между ними и поведения объекта во внешней среде привели к созданию больших технических и производственных (организационно-экономических) систем.
Современные машины обладают высокой конструктивно-функВнциональной сложностью, представляют собой технические компВнлексы, включающие огромное количество деталей, узлов, агрегаВнтов и готовых изделий, объединенных конечной функциональной целостностью. Конструктивно-функциональная сложность обусловВнливает высокую материалоемкость, трудоемкость, энергоемкость и стоимость технических комплексов. Развитие техники привело к созданию сложных иерархических структурных построений - больших технических систем. Это свойство технических комплекВнсов потребовало системного подхода к ее созданию, системного проектирования. В разрабатываемых технических комплексах конВнструкции отдельных входящих элементов должны быть подчинены общей цели, ради которой создается система, т. е. должна быть обеспечена единая стратегия поведения технической системы.
Создание больших технических систем вызвало в свою очередь появление больших организационно-экономических (производственных) систем, охватывающих множество предприятий, объВнединенных выпуском определенного технического комплекса. Возникает иерархия в структуре управления производственными предприятиями. Неуклонно нарастающие темпы развития науки и техники, создание современных организационно-экономических систем привели к лавинообразному росту информации и увеличеВннию степени нерегулярности ее поступления. Все это потребовало совершенствования методов планирования, создания системы планирования.
Важнейшими требованиями системного подхода являются комплексность прогнозов и планов и непрерывный характер проВнцесса планирования.
Комплексный подход предусматривает составление прогнозов и планов во взаимосвязи как в пространстве (в отраслевом и терВнриториальном разрезе), так и во времени. Взаимосвязь в простВнранстве означает установление рациональных отношений между отраслями народного хозяйства, экономическими районами, устаВнновление оптимальных соотношений между темпами развития науки, техники и промышленного производства, сбалансированВнность потребностей и ресурсов на всех уровнях иерархии.[3]
Взаимосвязь прогнозов и планов во времени обеспечивается реализацией принципа непрерывности планирования. Корректировка планов и прогнозов должна носить дискретный характер с заранее установленными сроками (режим функциониВнрования). Относительно частое изменение планов, обусловливаюВнщее изменение производственных программ, может привести к дезорганизации работы отраслей и предприятий в силу сложВнности структуры производственных связей в народном хозяйстве, большой трудоемкости и материалоемкости процессов подготовки промышленного производства.
Чувствительность прогноза и планов к изменениям зависит от уровня иерархии, сроков упреждения и периодичности корректиВнровок. Чем ниже уровень, тем чувствительность выше, тем должВнны быть короче периоды корректировки.
Важнейшим моментом внедрения и использования непрерывВнных систем планирования является определение качестваработы таких систем и на основе этого нахождение оптимального режима функционирования.
Непрерывность планирования обеспечивается путем реализаВнции принципа обратной связи. Корректировка планов и прогнозов проводится на основании информации обратной связи, содержаВнщей данные о результатах реализации планов, и прогнозов, уточнения потребностей, об изменении тенденции развития объекВнта и внешней среды (социально-политического, научно-техничеВнского и экономического фона).
Различная степень неопределенности вырабатываемой инфорВнмации о будущем влияет на характер применяемых методов, споВнсобов и приемов прогнозирования и планирования. Если при разработке планов предпочтение отдается детерминированным методам, то при прогнозировании - стохастическим. При составВнлении планов преимущественное применение имеют регулярные методы, при прогнозировании тАФ эвристические.
Специфика стадий и этапов планирования влияет также на количество и уровень агрегирования плановых и прогнозных показателей, степень их детерминированности, соотношения директивных и расчетных показателей.
2 МЕТОДЫ НАУЧНО-ТЕХНИЧЕСКОГО ПРОГНОЗИРОВАНИЯ
2.1 Классификация методов прогнозирования
Прежде всего приведем определение метода прогнозирования как способа теоретического и практического действия, направленВнного .на разработку прогнозов. Это определение является достаВнточно общим и позволяет понимать термин Влметод прогнозироваВннияВ» весьма широко: от простейших экстраполяционных расчетов до сложных процедур многошаговых экспертных опросов.
Для изучения методического аппарата прогностики целесообВнразно с самого начала детализировать это широкое понятие. Далее будем различать простые методы прогнозирования и комплексные методы прогнозирования. При этом под простым методом прогнозирования будем понимать метод, неразложимый на еще более простые методы прогнозироВнвания, и соответственно под комплексным - метод, состоящий из взаимосвязанной совокупности нескольких простых.
В настоящее время наряду со значительным числом опублиВнкованных методов прогнозирования известны многочисленные способы их классификации. Тем не менее считать этот вопрос удовлетворительно решенным нельзя, так как единой, полезной и полной классификации сейчас еще не создано. Вероятно, проВнгностика, как молодая наука, еще не достигла такого уровня разВнвития, когда возможно создание классификации, удовлетворяюВнщей всем этим требованиям. Итак, каковы же цели классификации методов прогностики? Можно указать две такие основные цели. Это, во-первых, обеспеВнчение процесса изучения и анализа методов и, во-вторых, обслуВнживание процесса выбора метода при разработке прогнозов объекта. На современном этапе трудно предложить единую класВнсификацию, в равной степени удовлетворяющую обеим из указанВнных целей.
Существуют два основных типа классификации: последоваВнтельная и параллельная. Последовательная классификация предВнполагает вычленение частных объемов из более общих. Это проВнцесс, тождественный делению родового понятия на видовые. При этом должны соблюдаться следующие основные правила: 1) осноВнвание деления (признак) должно оставаться одним и тем же при образовании любого видового понятия; 2) объемы видовых поняВнтий должны исключать друг друга (требование отсутствия переВнсечения классов); 3) объемы видовых понятий должны исчерпыВнвать объем родового понятия (требование полного охвата всех объектов классификации).
Параллельная классификация предполагает сложное инфорВнмационное основание, состоящее не из одного, а из целого ряда признаков. Основной принцип такой классификациитАФнезависиВнмость выбранных признаков, каждый из которых существен, все вместе одновременно присущи предмету и только их совокупность дает исчерпывающее представление о каждом классе.
Последовательная классификация имеет наглядную интерпреВнтацию в виде некоторого генеалогического дерева, охватывает всю рассматриваемую область в целом и определяет место и взаимоВнсвязи каждого класса в общей системе. Поэтому она является более приемлемой для целей изучения, позволяет методически более стройно представлять классифицируемую область знаний.
Каждый уровень классификации характеризуется своим класВнсификационным признаком. Элементы каждого уровня представВнляют собой наименования принадлежащих им подмножеств элементов ближайшего нижнего уровня, причем подмножеств непересекающихся.
Элементы нижнего уровня представляют собой наименование узких групп конкретных методов прогнозирования (иногда из одного элемента), которые являются модификациями или разноВнвидностями какого-либо одного, наиболее общего из них.
В целом классификация является открытой, так как представВнляет возможность увеличивать число элементов на уровнях и наращивать число уровней за счет дальнейшего дробления и уточнения элементов последнего уровня.
На первом уровне все методы делятся на три класса по приВнзнаку Влинформационное основание методаВ». Фактографическиеметоды базируются на фактически имеющемся информационном материале об объекте прогнозирования и его прошлом развитии. Экспертные методы базируются на информации, которую поставВнляют специалисты-эксперты в процессе систематизированных проВнцедур выявления и обобщения этого мнения. Комбинированныеметоды выделены в отдельный класс, чтобы можно было отноВнсить к нему методы со смешанной информационной основой, в которых в качестве первичной информации используются фактографическая и экспертная. Например, при проведении экспертного опроса участникам представляют цифровую информацию об объекте или фактографические прогнозы, либо, наоборот, при экстраполяции тенденции наряду с фактическими данными используют экспертные оценки.
Не следует относить к комбинированным методам те методы прогнозирования, которые к экспертной исходной информации применяют математические методы обработки или исходную факВнтографическую информацию оценивают экспертным путем. В большинстве случаев они достаточно хорошо укладываются в первый или второй из перечисленных выше классов.[2]
Эти классы разделяются далее на подклассы по принципам обработки информации. Статистические методы объединяют совоВнкупность методов обработки количественной информации об объекте прогнозирования по принципу выявления содержащихся в ней математических закономерностей развития и математичеВнских взаимосвязей характеристик с целью получения прогнозных моделей. Методы аналогий направлены на то, чтобы выявлять сходство в закономерностях развития различных процессов и на этом основании производить прогнозы. Опережающие методы проВнгнозирования строятся на определенных принципах специальной обработки научно-технической информации, реализующих в проВнгнозе ее свойство опережать развитие научно-технического проВнгресса.
Экспертные методы разделяются на два подкласса. Прямые экспертные оценки строятся по принципу получения и обработки независимого обобщенного мнения коллектива экспертов (или одного из них) при отсутствии воздействий на мнение каждого эксперта мнения другого эксперта и мнения коллектива. ЭкспертВнные оценки с обратной связью в том или ином виде воплощают принцип обратной связи путем воздействия на оценку экспертной группы (одного эксперта) мнением, полученным ранее от этой группы или от одного из ее экспертов.
Третий уровень классификации разделяет методы прогнозироВнвания на виды по классификационному признаку Влаппарат метоВндовВ». Каждый вид объединяет в своем составе методы, имеющие в качестве основы одинаковый аппарат их реализации. Так, стаВнтистические методы по видам делятся на методы экстраполяции и интерполяции; методы, использующие аппарат регрессионного и корреляционного анализа; методы, использующие факторный анализ.
Класс методов аналогий подразделяется на методы математиВнческих и исторических аналогий. Первые в качестве аналога для объекта прогнозирования используют объекты другой физической природы, другой области науки, отрасли техники, однако имеюВнщие математическое описание процесса развития, совпадающее с объектом прогнозирования. Вторые в качестве аналога испольВнзуют процессы одинаковой физической природы, опережающие во времени развитие объекта прогнозирования.
Опережающие методы прогнозирования можно разделить на методы исследования динамики научно-технической информации; методы исследования и оценки уровня техники. В первом случае в основном используется построение количественно-качественных динамических рядов на базе различных видов НТИ и анализа и прогнозирования на их основе соответствующего объекта. ВтоВнрой вид методов использует специальный аппарат анализа колиВнчественной и качественной информации, содержащейся в НТИ, для определения характеристик уровня, качества существующей и проВнектируемой техники.
Прямые экспертные оценки по признаку аппарата реализации делятся на виды экспертного опроса и экспертного анализа. В первом случае используются специальные процедуры формироВнвания вопросов, организации получения на них ответов, обработВнки полученных ответов и формирования окончательного резульВнтата. Во втором тАФ основным аппаратом исследования является целенаправленный анализ объекта прогнозирования со стороны эксперта или коллектива экспертов, которые сами ставят и решаВнют вопросы, ведущие к поставленной цели.
Экспертные оценки с обратной связью в своём аппарате имеВнют три вида методов: экспертный опрос; генерацию идей; игровое моделирование. Первый вид характеризуется процедурами реглаВнментированного неконтактного опроса экспертов перемежающимиВнся обратными связями в рассмотренном выше смысле. Второй тАФ построен на процедурах непосредственного общения экспертов в процессе обмена мнениями по поставленной проблеме. Он характеризуется отсутствием вопросов и ответов и направлен на взаимное стимулирование творческой деятельности экспертов. Третий вид использует аппарат теории игр и ее прикладных разВнделов. Как правило, реализуется на сочетании динамического взаимодействия коллективов экспертов и вычислительной машиВнны, имитирующих объект прогнозирования в возможных будущих ситуациях.
Наконец, последний, четвертый, уровень классификации подВнразделяет виды методов третьего уровня на отдельные методы и группы методов по некоторым локальным для каждого вида совокупностям классификационных признаков, из которых укаВнзать один общий для всего уровня в целом невозможно.
2.2 Экстраполяционные методы прогнозирования
Методы экстраполяции тенденций являются, пожалуй, самыми распространенными и наиболее разработанными среди всей совоВнкупности методов прогнозирования. Использование экстраполяции в прогнозировании имеет в своей основе .предположение о том, что рассматриваемый процесс изменения переменной представляВнет собой сочетание двух составляющихтАФрегулярной и случайной:
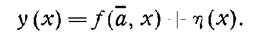(1.2.2)
Считается, что регулярная составляющая f(a, х) представляет собой гладкую функцию от аргумента (в большинстве случаевтАФ времени), описываемую конечномерным вектором параметров а, которые сохраняют свои значения на периоде упреждения проВнгноза. Эта составляющая называется также трендом, уровнем, детерминированной основой процесса, тенденцией. Под всеми этими терминами лежит интуитивное представление о какой-то очищенной от помех сущности анализируемого процесса. ИнтуиВнтивное, потому что для большинства экономических, технических, природных процессов нельзя однозначно отделить тренд от слуВнчайной составляющей. Все зависит от того, какую цель преслеВндует это разделение и с какой точностью его осуществлять.
Случайная составляющая n(х) обычно считается некоррелиВнрованным случайным процессом с нулевым математическим ожиВнданием. Ее оценки необходимы для дальнейшего определения точностных характеристик прогноза.
Экстраполяционные методы прогнозирования основной упор делают на выделение наилучшего в некотором смысле описания тренда и на определение прогнозных значений путем его экстраВнполяции. Методы экстраполяции во многом пересекаются с метоВндами прогнозирования по регрессионным моделям. Иногда их различия сводятся лишь к различиям в терминологии, обозначеВнниях или написании формул. Тем не менее сама по себе прогнозная экстраполяция имеет ряд специфических черт и приемов, позвоВнляющих причислять ее к некоторому самостоятельному виду методов прогнозирования.
Специфическими чертами прогнозной экстраполяции можно назвать методы предварительной обработки числового ряда с целью преобразования его к виду, удобному для прогнозироваВнния, а также анализ логики и физики прогнозируемого процесса, оказывающий существенное влияние как па выбор вида экстраВнполирующей функции, так и на определение границ изменения ее параметров.
2.2.1 Предварительная обработка исходной информации в задачах прогнозной экстраполяции
Предварительная обработка исходного числового ряда направВнлена на решение следующих задач (всех или части из них): сниВнзить влияние случайной составляющей в исходном числовом ряду, т. е. приблизить его к тренду; представить информацию, содержащуюся в числовом ряду, в таком виде, чтобы существенно снизить трудность математического описания тренда. Основными методами решения этих задач являются процедуры сглаживания и выравнивания статистического ряда.
Процедура сглаживания направлена на минимизацию случайВнных отклонений точек ряда от некоторой гладкой кривой предВнполагаемого тренда процесса. Наиболее распространен способ осреднения уровня по некоторой совокупности окружающих точек, причем эта операция перемещается вдоль ряда точек, в связи с чем обычно называется скользящая средняя. В самом простом варианте сглаживающая функция линейна и сглаживающая групВнпа состоит из предыдущей и последующей точек, в более сложВнных тАФ функция нелинейна и использует группу произвольного числа точек.
Сглаживание производится с помощью многочленов, приблиВнжающих по методу наименьших квадратов группы опытных точек. Наилучшее сглаживание получается для средних точек группы, поэтому желательно выбирать нечетное количество точек в сглаживаемой группе.
Сглаживание даже в простом линейном варианте является во многих случаях весьма эффективным средством выявления тренда при наложении на эмпирический числовой ряд случайных помех и ошибок измерения. Для рядов со значительной амплиВнтудой помехи имеется возможность проводить многократное сглаВнживание исходного числового ряда. Число последовательных циклов сглаживания должно выбираться в зависимости от вида исходного ряда, от степени предполагаемой его зашумленности помехой, от цели, которую преследует сглаживание. Надо иметь при этом в виду, что эффективность этой процедуры быстро уменьшается (в большинстве случаев), так что целесообразно повторять ее от одного до трех раз.
Линейное сглаживание является достаточно грубой процедуВнрой, выявляющей общий приблизительный вид тренда. Для более точного определения формы сглаженной кривой может применятьВнся операция нелинейного сглаживания или взвешенные скользящие средние. В этом случае ординатам точек, входящих в скольВнзящую группу, приписываются различные веса в зависимости от их расстояния от середины интервала сглаживания.
Если сглаживание направлено на первичную обработку числоВнвого ряда для исключения случайных колебаний и выявления тренда, то выравнивание служит целям более удобного представВнления исходного ряда, оставляя прежними его значения.
Наиболее общими приемами выравнивания являются логарифВнмирование и замена переменных.
В случае если эмпирическая формула предполагается содерВнжащей три параметра либо известно, что функция трехпараметВнрическая, иногда удается путем некоторых преобразований искВнлючить один из параметров, а оставшиеся два привести к одной из формул выравнивания.
Можно рассматривать выравнивание не только как метод представления исходных данных, но и как метод непосредственВнного приближенного определения параметров функции, аппроксиВнмирующей исходный числовой ряд. Зачастую именно так и используется этот метод в некоторых экстраполяционных проВнгнозах. Отметим, что возможность непосредственного его испольВнзования для определения параметров аппроксимирующей функВнции определяется главным образом видом исходного числового ряда и степенью наших знаний, нашей уверенности относительно вида функции, описывающей исследуемый процесс.
В том случае, если вид функции нам неизвестен, выравниваВнние следует рассматривать как предварительную процедуру, в процессе которой путем применения различных формул и приеВнмов выясняется наиболее подходящий вид функции, описывающей эмпирический ряд.
Одной из разновидностей метода выравнивания является исследование эмпирического ряда с целью выяснения некоторых свойств функции, описывающей его. При этом не обязательно преобразования приводят к линейным формам. Однако результаВнты их подготавливают и облегчают процесс выбора аппроксимиВнрующей функции в задачах прогностической экстраполяции. В простейшем случае предлагается использовать следующие три типа дифференциальных функций роста:
1) Первая производная, или абсолютная дифференциальная функция роста.
2) Относительный дифференциальный коэффициент, или логаВнрифмическая производная,
3) Эластичность функции
2.3 Статистические методы
Прежде чем приступить к анализу статистических методов прогнозирования, рассмотрим некоторые общие понятия и опредеВнления, относящиеся к корреляционным и регрессионным моделям. Две случайные величины являются корреляционно связанВнными, если математическое ожидание одной из них меняется в завиВнсимости от изменения другой.
Применение корреляционного анализа предполагает выполнеВнние следующих предпосылок:
а) Случайные величины y(y1, у2, .., Уn) и x(x1, x2, .., Хn) могут рассматриваться как выборка из двумерной генеральной совокупВнности с нормальным законом распределения.
б) Ожидаемая величина погрешности и равна нулю
в) Отдельные наблюдения стахостически независимы, т. е. знаВнчение данного наблюдения не должно зависеть от значения предыВндущего и последующего наблюдений.
г) Ковариация между ошибкой, связанной с одним значением зависимой переменной у, и ошибкой, связанной с любым другим значением y , равна нулю.
д) Дисперсия ошибки, связанная с одним значением у, равна дисперсии ошибки, связанной с любым другим значением .
е) Ковариация между погрешностью и каждой из независимых переменных равна нулю.
ж) Непосредственная применимость этого метода ограничивается случаями, когда уравнение кривой является линейным относительно своих параметров bo, bi, ..,bk Это, однако, не означает, что само уравнение кривой относительно переменных должно быть линейВнным. Если эмпирические уравнения наблюдений не являются линейными, то во многих случаях оказывается возможным приВнвести их к линейной форме и уже. после этого применять метод наименьших квадратов.
з) Наблюдения независимых переменных производятся без погрешности.
Перед началом корреляционного анализа необходимо проверить выполнение этих предпосылок.
Связь между случайной и неслучайной величинами называется регрессионной, а метод анализа таких связей тАФ регрессионным анализом. Применение регрессионного анализа предполагает обяВнзательное выполнение предпосылок (б-г) корреляционВнного анализа. Только при выполнении приведенных предпосылок оценки коэффициентов корреляции и регрессии, получаемые с помощью способа наименьших квадратов, будут несмещенными и иметь минимальную дисперсию.
Регрессионный анализ тесно связан с корреляционным. При выполнении предпосылок корреляционного анализа выполняются предпосылки регрессионного анализа. В то же время регрессионный анализ предъявляет менее жесткие требования к исходной инфорВнмации.В» Так, например, проведение регрессионного анализа возВнможно даже в случае отличия распределения случайной величины от нормального, как это часто бывает для технико-экономических величин. В качестве зависимой переменной в регрессионном анаВнлизе используется случайная переменная, а в качестве независиВнмой тАФ неслучайная переменная.
По степени комплексности статистические исследования можно разделить на двумерные и многомерные. Первые касаются рассмотВнрения парных взаимосвязей между переменными (парные корреВнляции и регрессии) и направлены в прогнозных исследованиях на решение таких задач, как установление количественной меры тесВнноты связи между двумя случайными величинами, установление близости этой связи к линейной, оценки достоверности и точности прогнозов, полученных экстраполяцией регрессионной зависимоВнсти. Многомерные методы статистического - анализа направлены в основном на решение задачи системного анализа многомерных стохастических объектов прогнозирования. Целью такого анализа является, как правило, выяснение внутренних взаимосвязей между переменными комплекса, построение многомерных функций связи переменных, выделение минимального числа характеристик, описыВнвающих объект с достаточной степенью точности. Одной из основВнных задач здесь является сокращение размерности описания объВнекта прогнозирования.
Таким образом, статистические методы используются в основВнном для подготовки данных, приведения их к виду, пригодному для производства прогноза. Как правило, после их применения испольВнзуется один из методов экстраполяции или интерполяции для полуВнчения непосредственно прогнозного результата.
2.4 Экспертные методы
2.4.1 Область применения экспертных методов
Методы экспертных оценок в прогнозировании и перспективном планировании научно-технического прогресса применяются в слеВндующих случаях:
а) в условиях отсутствия достаточно представительной и достоВнверной статистики характеристики объекта (например,
Вместе с этим смотрят:
"Стена безопасности" между Израилем и Палестиной
"Хезболла" как инструмент ИРИ в эскалации арабо-израильского конфликта
"Холодная война": идеологические и геополитические факторы ее возникновения
"Этап реформ" в Саудовской Аравии
Globalization and Hospitality Industry