Визначення динамiчних похибок вимiрювань
Мiнiстерство освiти i науки Украiни
Вiнницький нацiональний технiчний унiверситет
РЖнститут автоматики, електронiки та комптАЩютерних систем управлiння
Кафедра МПА
ВИЗНАЧЕННЯ ДИНАМРЖЧНИХ ПОХИБОК ВИМРЖРЮВАНЬ
Пояснювальна записка
з дисциплiни тАЬОснови теорii похибок та обробки результатiв вимiрюваньтАЭ
до курсовоi роботи за спецiальнiстю 8.091302
тАЬМетрологiя та вимiрювальна технiкатАЭ
08-03.ОТПОРВ.007.00.000 ПЗ
Вiнниця ВНТУ 2007
Змiст
Вступ
1. Характеристики точностi та правильностi вимiрювань
2. Практична частина
Висновки
Перелiк посилань
Додатки
Додаток А. РозвтАЩязок диференцiйного рiвняння в пакетi Maple 7
ВСТУП
При проведеннi вимiрювань завжди виникаi перехiдний процес, при якому сигнал на виходi засобу вимiрювання суттiво змiнюiться в часi. Це пояснюiться iнерцiйними властивостями засобу вимiрювання, якi зумовлюють виникнення динамiчноi похибки тАУ складовоi похибки вимiрювання, що виникаi додатково до статичноi похибки при проведеннi динамiчних вимiрювань.
Динамiчна похибка представляiться через динамiчнi характеристики та визначаiться як миттiва рiзниця значення вихiдного сигналу, розрахованого за вхiдним сигналом, i миттiвого значення вихiдного сигналу в даний момент часу.
Для визначення динамiчноi похибки необхiдно знайти повнi динамiчнi характеристики засобу вимiрювання, а саме диференцiальне рiвняння, перехiдну, iмпульсну, амплiтудно-частотну та фазочастотну характеристики, оскiльки саме повнi динамiчнi характеристики однозначно визначають змiни вихiдного сигналу засобу вимiрювання при будь-яких змiнах у часi вхiдного сигналу або впливних величин.
1. ХАРАКТЕРИСТИКИ ТОЧНОСТРЖ ТА ПРАВИЛЬНОСТРЖ ВИМРЖРЮВАНЬ
Точнiсть вимiрювань тАУ це характеристика ii якостi, що вiдображаi близькiсть результату вимiрювань до iстинного значення вимiрюваноi фiзичноi величини. Точнiсть виражають оберненим значенням модуля вiдносноi похибки вимiрювання
![]() .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.1)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.1)
Точнiсть засобу вимiрювальноi технiки характеризуiться його класом точностi тАУ узагальненою характеристикою, що визначаiться границями допустимоi основноi та зведеноi похибок, а також iншими характеристиками, що впливають на його точнiсть, значення яких регламентуiться.
Засобам вимiрювань з двома чи бiльшою кiлькiстю дiапазонiв вимiрювань даноi фiзичноi величини допускаiться присвоювати два i бiльше класiв точностi. Засобам вимiрювання, що призначенi для вимiрювання двох i бiльше фiзичних величин, також допускаiться присвоювати рiзнi класи точностi для кожноi фiзичноi величини.
Границi допустимих основноi та додатковоi похибок засобiв вимiрювання встановлюють у формi абсолютних, зведених або вiдносних значень, залежно вiд характеру iх звтАЩязку з iнформативним параметром вхiдного чи вихiдного сигналiв.
Границi допустимоi абсолютноi основноi похибки встановлюють за формулами
![]() ВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.2)
ВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.2)
![]() .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.3)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.3)
де ![]() ВатАУ границi допустимоi абсолютноi основноi похибки, що встановлена в одиницях вхiдноi чи вихiдноi величини або умовно в подiлках шкали;
ВатАУ границi допустимоi абсолютноi основноi похибки, що встановлена в одиницях вхiдноi чи вихiдноi величини або умовно в подiлках шкали; ![]() ВатАУ значення вхiдноi чи вихiдноi величин засобу вимiрювання чи кiлькiсть подiлок шкали;
ВатАУ значення вхiдноi чи вихiдноi величин засобу вимiрювання чи кiлькiсть подiлок шкали; ![]() Ваi
Ваi ![]() ВатАУ додатнi числа, якi не залежать вiд
ВатАУ додатнi числа, якi не залежать вiд ![]() .
.
Границi основноi зведеноi похибки встановлюються за формулою
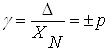 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.4)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.4)
де ![]() ВатАУ границi допустимоi зведеноi основноi похибки;
ВатАУ границi допустимоi зведеноi основноi похибки; ![]() ВатАУ границi допустимоi абсолютноi основноi похибки;
ВатАУ границi допустимоi абсолютноi основноi похибки; ![]() ВатАУ нормувальне значення, яке вибирають залежно вiд характеру шкали;
ВатАУ нормувальне значення, яке вибирають залежно вiд характеру шкали; ![]() ВатАУ абстрактне число з ряду [1; 1,5 (1,6); 2; 2,5 (3); 4; 5; 6]
ВатАУ абстрактне число з ряду [1; 1,5 (1,6); 2; 2,5 (3); 4; 5; 6] ![]() .
.
Значення, якi стоять у дужках, для засобiв вимiрювань, якi розробляються заново, не використовуються.
Нормувальне значення ![]() Вадля засобiв вимiрювання з рiвномiрною, практично рiвномiрною чи степеневою шкалою i для вимiрювальних перетворювачiв встановлюють такими, що дорiвнюють: бiльшiй з границь вимiрювань; бiльшому з модулiв границь вимiрювань, якщо нульове значення знаходиться всерединi дiапазону вимiрювань (для електровимiрювальних приладiв допускаiться встановити таке значення, що дорiвнюi сумi модулiв границь вимiрювань).
Вадля засобiв вимiрювання з рiвномiрною, практично рiвномiрною чи степеневою шкалою i для вимiрювальних перетворювачiв встановлюють такими, що дорiвнюють: бiльшiй з границь вимiрювань; бiльшому з модулiв границь вимiрювань, якщо нульове значення знаходиться всерединi дiапазону вимiрювань (для електровимiрювальних приладiв допускаiться встановити таке значення, що дорiвнюi сумi модулiв границь вимiрювань).
Для засобiв вимiрювання фiзичноi величини, для яких прийнята шкала з умовним нулем, нормувальне значення дорiвнюi рiзницi границь вимiрювань.
Для вимiрювальних приладiв з суттiво нерiвномiрною шкалою нормувальне значення встановлюють рiвним всiй довжинi шкали або ii частинi, що вiдповiдаi дiапазону вимiрювань. При цьому границi абсолютноi похибки встановлюють, як i довжину шкали, в одиницях довжини.
Границi допустимоi вiдносноi похибки встановлюються за формулою:
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.5)
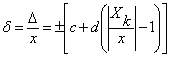 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.6)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.6)
де ![]() ВатАУ границi допустимоi вiдносноi основноi похибки;
ВатАУ границi допустимоi вiдносноi основноi похибки; ![]() ВатАУ значення вимiрюваноi величини;
ВатАУ значення вимiрюваноi величини; ![]() ,
, ![]() Вата
Вата ![]() ВатАУ абстрактнi додатнi числа, вибранi з того ж ряду, що i
ВатАУ абстрактнi додатнi числа, вибранi з того ж ряду, що i ![]() Ва(для зведеноi похибки);
Ва(для зведеноi похибки); ![]() ВатАУ бiльша (за модулем) iз границь вимiрювань.
ВатАУ бiльша (за модулем) iз границь вимiрювань.
Для цифрових приладiв клас точностi переважно вiдображений двома числами, що записанi через косу риску ![]() . Цi числа вiдображають вираженi у вiдсотках границi основноi зведеноi похибки
. Цi числа вiдображають вираженi у вiдсотках границi основноi зведеноi похибки ![]()
![]() :
: ![]() ВатАУ на початку (при нульовому значеннi
ВатАУ на початку (при нульовому значеннi ![]() ), а
), а ![]() ВатАУ в кiнцi границi вимiрювання (показ
ВатАУ в кiнцi границi вимiрювання (показ ![]() ):
):
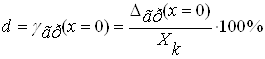 ,ВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (1.7)
,ВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (1.7)
 .ВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.8)
.ВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.8)
Для промiжних показiв (![]() ) границi зведеноi похибки приладу змiнюються лiнiйно. Таке нормування зумовлено тим, що для цифрових приладiв характерна як адитивна (що не залежить вiд значення вимiрюваноi величини), так i мультиплiкативна (що лiнiйно, прямо пропорцiйно залежить вiд значення вимiрюваноi величини) похибки.
) границi зведеноi похибки приладу змiнюються лiнiйно. Таке нормування зумовлено тим, що для цифрових приладiв характерна як адитивна (що не залежить вiд значення вимiрюваноi величини), так i мультиплiкативна (що лiнiйно, прямо пропорцiйно залежить вiд значення вимiрюваноi величини) похибки.
Вiдповiдно до означення зведеноi похибки за класом точностi (![]() ), показом
), показом ![]() Вата границею вимiрювання
Вата границею вимiрювання ![]() Вав явному виглядi можна встановити границi абсолютноi
Вав явному виглядi можна встановити границi абсолютноi
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.9)
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.10)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.10)
Границi допустимоi додатковоi похибки засобiв вимiрювання можна встановити в формi , що вiдрiзняiться вiд форми встановлення границь допустимоi основноi похибки. РЗх встановлюють:
У виглядi сталого значення для всього дiапазону значень виливноi величини або сталих значень для певних iнтервалiв цього дiапазону.
Зазначенням вiдношення границi допустимоi додатковоi похибки, що вiдповiдаi регламентованому iнтервалу значень впливноi величини, до ширини цього iнтервалу.
Наведенням граничноi функцii впливу як залежностi границь допустимоi додатковоi похибки вiд впливних величин.
Наведенням функцiональноi залежностi границь допустимих вiдхилень вiд номiнальноi функцii впливу.
Правильнiсть вимiрювання тАУ це характеристика його якостi, що вiдображаi близькiсть до нуля систематичноi похибки в його результатi. Якщо значення систематичноi складовоi ![]() Вапохибки
Вапохибки ![]() Вавiдоме, то результат вимiрювання можна виправити введенням поправлення
Вавiдоме, то результат вимiрювання можна виправити введенням поправлення
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.11)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.11)
Поправлення тАУ значення фiзичноi величини, яке додаiться до результату вимiрювання, щоб виключити систематичну похибку. Поправлення пiдсумовують iз значенням мiри, показом вимiрювального приладу тощо. РЖнодi замiсть поправлення значення фiзичноi величини користуються поправляльним множником ![]() , на який перемножують вимiряну фiзичну величину
, на який перемножують вимiряну фiзичну величину ![]() , з метою вилучення з неi систематичноi похибки, тобто для виконання умов
, з метою вилучення з неi систематичноi похибки, тобто для виконання умов
![]() Ва ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.12)
Ва ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.12)
Сукупними характеристиками точностi i правильностi вимiрювань i iх вiдтворюванiсть i збiжнiсть. Вiдтворюванiсть вимiрювань тАУ це близькiсть результатiв вимiрювань сталоi фiзичноi величини отриманих у рiзних умовах, рiзними методами, засобами вимiрювань, експериментаторами незалежно вiд мiсця та часу iх здiйснення, тобто нерiвноточних вимiрювань, в яких систематична складова iх похибки стаi випадковою. Збiжнiстю вимiрювань називають iх вiдтворюванiсть в однакових умовах (рiвноточнi вимiрювання). Збiжнiсть результатiв вимiрювань вiдображаi близькiсть до нуля випадковоi похибки вимiрювань. Збiжнiсть може бути оцiнена кiлькiсно дисперсiiю результатiв вимiрювання.
Видiляють ще термiн роздiльноi (подiльноi) здатностi засобу вимiрювальноi технiки як кiлькостi вiрогiдно розрiзнюваних значень вимiрюваноi фiзичноi величини, якi вписуються в зону iх невизначеностi в процесi вимiрювань. Для такого означення термiну роздiльноi здатностi засобу вимiрювальноi технiки визначають також ступiнь вiрогiдностi, з якою встановлюiться ширина зони невизначеностi ![]() Вапохибок результатiв вимiрювань (рисунок 1.1), тобто значення гарантiйноi ймовiрностi
Вапохибок результатiв вимiрювань (рисунок 1.1), тобто значення гарантiйноi ймовiрностi ![]() , з якою визначають цi похибки. Зону невизначеностi знаходять для сумарноi похибки чи гарантiйноi похибки для заданого значення надiйностi
, з якою визначають цi похибки. Зону невизначеностi знаходять для сумарноi похибки чи гарантiйноi похибки для заданого значення надiйностi ![]() .
.
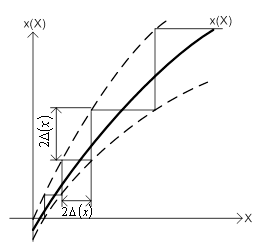
Рисунок 1.1 тАУ Графiчна iнтерпретацiя роздiльноi здатностi
Роздiльна здатнiсть вимiрювань i теоретичною характеристикою, що залежить вiд точностi та дiапазону вимiрювань.
2. ПРАКТИЧНА ЧАСТИНА
Динамiчне рiвняння повтАЩязуi вихiдну величину ![]() Вазасобу вимiрювання iз вхiдною
Вазасобу вимiрювання iз вхiдною ![]() Вав динамiчному режимi роботи. При його складаннi в праву частину рiвняння записують вхiдний сигнал (причину, що привела засiб вимiрювання в дiю), а в лiву тАУ вихiдний сигнал (реакцiю засобу вимiрювання). В загальному виглядi диференцiальне рiвняння маi вигляд:
Вав динамiчному режимi роботи. При його складаннi в праву частину рiвняння записують вхiдний сигнал (причину, що привела засiб вимiрювання в дiю), а в лiву тАУ вихiдний сигнал (реакцiю засобу вимiрювання). В загальному виглядi диференцiальне рiвняння маi вигляд:
![]() ВаВаВаВаВаВаВаВаВаВаВа (2.1)
ВаВаВаВаВаВаВаВаВаВаВа (2.1)
В операторнiй формi
![]() ВаВаВаВаВаВа (2.2)
ВаВаВаВаВаВа (2.2)
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
Диференцiальне рiвняння динамiчноi системи i вичерпною ii характеристикою, але його коефiцiiнти важко пiддаються експериментальному визначенню. Тому як характеристики перетворення в часовiй областi використовуються iмпульсна перехiдна (вагова) ![]() Вата перехiдна
Вата перехiдна ![]() Вафункцii.
Вафункцii.
РЖмпульсна функцiя ![]() Ваi вiдгуком (реакцiiю) динамiчноi системи на вхiдне збурення у виглядi
Ваi вiдгуком (реакцiiю) динамiчноi системи на вхiдне збурення у виглядi ![]() -функцii, яка за визначенням маi властивостi
-функцii, яка за визначенням маi властивостi
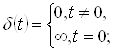 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)
Перехiдна функцiя
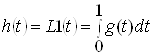 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.6)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.6)
i вiдгуком динамiчноi системи на вхiдну дiю у виглядi одиничноi функцii ![]() , похiдна якоi
, похiдна якоi
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.7)
З характеристиками перетворення у часовiй областi однозначно повтАЩязанi характеристики перетворення в частотнiй областi, що i наслiдком дуальностi часу i частоти.
Усталена реакцiя на синусоiдний вхiдний сигнал у загальному випадку i складною функцiiю параметрiв засобу вимiрювальноi технiки i описуiться вiдповiдними амплiтудно-частотною та фазочастотною характеристиками, якi можуть бути одержанi з диференцiального рiвняння в результатi нижчеподаних математичних дiй.
Застосувавши до диференцiального рiвняння при початкових нульових умовах перетворення Лапласа, одержимо передаточну функцiю
 Ва ВаВаВаВаВаВаВаВа (2.8)
Ва ВаВаВаВаВаВаВаВа (2.8)
де ![]() Ва- оператор Лапласа,
Ва- оператор Лапласа, ![]() Вата
Вата ![]() Ва- зображення за Лапласом вiдповiдно вихiдноi та вхiдноi величин.
Ва- зображення за Лапласом вiдповiдно вихiдноi та вхiдноi величин.
Замiна оператора Лапласа в передаточнiй функцii на ![]() Вадаi комплексну частотну характеристику
Вадаi комплексну частотну характеристику
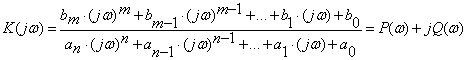 (2.9)
(2.9)
Комплексна частотна характеристика i вихiдною для визначення амплiтудно-частотноi
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)
![]() ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.11)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.11)
Згiдно iндивiдуального завдання необхiдно знайти розвтАЩязок диференцiального рiвняння другого порядку
![]() ,ВаВаВаВаВаВаВаВаВаВаВаВа (2.12)
,ВаВаВаВаВаВаВаВаВаВаВаВа (2.12)
![]() .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.13)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.13)
Пiдставимо (2.13) в (2.12) i отримаiмо:
![]() .ВаВаВаВаВаВаВаВаВа (2.14)
.ВаВаВаВаВаВаВаВаВа (2.14)
РозвтАЩязком даного рiвняння буде функцiя
![]()
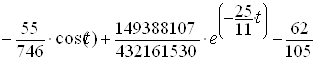 ,ВаВаВаВаВаВаВаВаВаВа (2.15)
,ВаВаВаВаВаВаВаВаВаВа (2.15)
графiчне зображення якоi подано на рисунку 2.1.
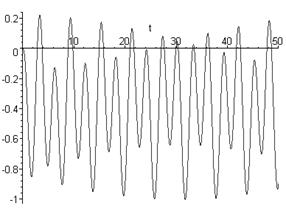
Рисунок 2.1 тАУ Графiчне представлення розвтАЩязку диференцiального рiвняння
Для знаходження перехiдноi характеристики пiдставимо в (2.12) як вхiдний сигнал ![]() :
:
![]()
![]() .Ва (2.16)
.Ва (2.16)
Отримаiмо розвтАЩязок:
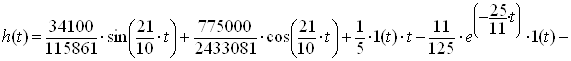
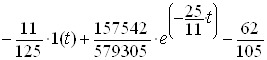 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.17)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.17)
Графiчно перехiдна характеристика зображена на рисунку 2.2.
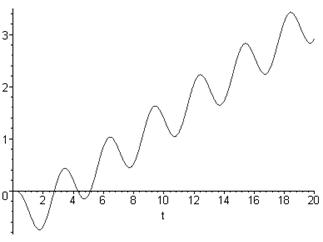
Рисунок 2.2 тАУ Перехiдна характеристика
Для знаходження iмпульсноi характеристики пiдставимо в (2.12) як вхiдний сигнал ![]() :
:
![]() .ВаВаВаВаВаВаВаВаВаВаВаВа (2.18)
.ВаВаВаВаВаВаВаВаВаВаВаВа (2.18)
Отримаiмо розвтАЩязок:
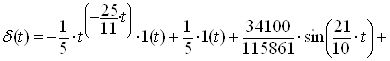
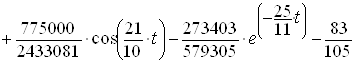 ВаВаВаВаВаВаВаВаВаВаВаВа (2.19)
ВаВаВаВаВаВаВаВаВаВаВаВа (2.19)
Графiчно iмпульсна характеристика зображена на рисунку 2.3.
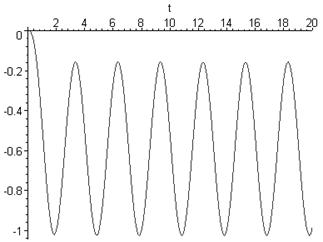
Рисунок 2.3 тАУ РЖмпульсна характеристика
Знайдемо передатну функцiю заданого диференцiального рiвняння
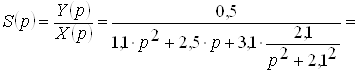
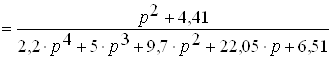 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.20)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.20)
Замiнимо оператор Лапласа в передатнiй функцii на ![]() Вата отримаiмо комплексну частотну характеристику
Вата отримаiмо комплексну частотну характеристику
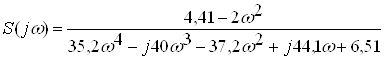 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.21)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.21)
Видiлимо дiйсну та уявну частини в знаменнику:
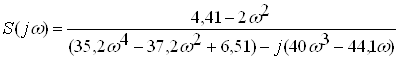 .ВаВаВаВаВаВаВаВаВаВаВаВа (2.22)
.ВаВаВаВаВаВаВаВаВаВаВаВа (2.22)
Помножимо чисельник та знаменник дробу на вираз, комплексно спряжений до знаменника, для того, щоб позбутись iррацiональностi в знаменнику. В результатi отримаiмо
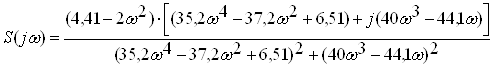 .ВаВаВа (2.23)
.ВаВаВа (2.23)
З даного виразу маiмо дiйсну
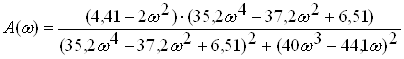 ВаВаВаВаВаВаВаВаВаВаВаВа (2.24)
ВаВаВаВаВаВаВаВаВаВаВаВа (2.24)
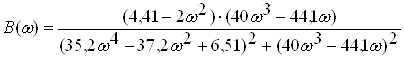 .ВаВаВаВаВаВаВаВаВаВаВа (2.25)
.ВаВаВаВаВаВаВаВаВаВаВа (2.25)
частини комплексноi частотноi характеристики.
Знайдемо амплiтудно-частотну характеристику як корiнь iз суми пiднесених до квадрату дiйсноi та уявноi частин комплексноi частотноi характеристики:
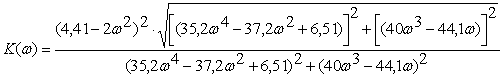 .Ва (2.26)
.Ва (2.26)
Замiнимо ![]() , тодi
, тодi
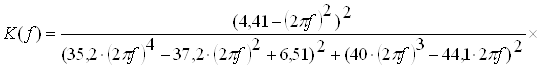
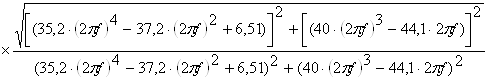 Ва(2.27)
Ва(2.27)
Графiчно амплiтудно-частотну характеристику наведено на рисунку 2.4.
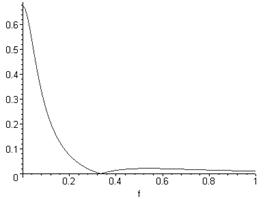
Рисунок 2.4 тАУ Амплiтудно-частотна характеристика
Знайдемо фазочастотну характеристику як мiнус арктангенс вiдношення уявноi частини комплексноi частотноi характеристики до дiйсноi
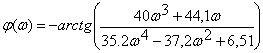 .ВаВа ВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (2.28)
.ВаВа ВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (2.28)
Пiсля замiни ![]() Ваотримаiмо
Ваотримаiмо
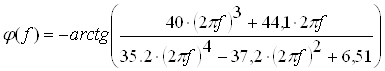 .ВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (2.29)
.ВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (2.29)
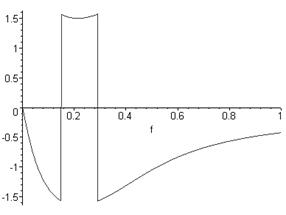
Графiк фазочастотноi характеристики наведено на рисунку 2.5.
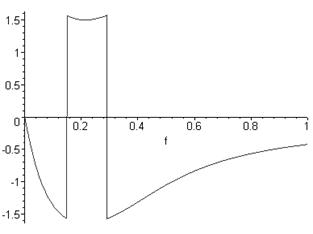
Рисунок 2.5 тАУ Фазочастотна характеристика
Отже, в даному роздiлi було знайдено розвтАЩязок диференцiального рiвняння другого порядку, отримано перехiдну, iмпульсну, амплiтудно-частотну та фазочастотну характеристики. Всi розвтАЩязки отриманi за допомогою пакету прикладних програм Maple 7 i наведенi в додатку А.
ВИСНОВКИ
В данiй курсовiй розглянуто питання визначення динамiчних похибок вимiрювання за допомогою динамiчних характеристик засобу вимiрювання.
В першому роздiлi розглянуто характеристики точностi та правильностi вимiрювань, дано iнтерпретацiю понять роздiльноi здатностi та класу точностi засобу вимiрювання, наведено методики визначення класу точностi для рiзних типiв засобiв вимiрювання.
В другому роздiлi було знайдено розвтАЩязок диференцiального рiвняння другого порядку, що описуi залежнiсть вихiдного сигналу засобу вимiрювання вiд вхiдного, отримано перехiдну, iмпульсну, амплiтудно-частотну та фазочастотну характеристики, оскiльки саме вони як повнi динамiчнi характеристики дозволяють визначити динамiчну похибку засобу вимiрювання.
Всi розвтАЩязки отриманi за допомогою пакету прикладних програм Maple 7 i наведенi в додатку А.
ПЕРЕЛРЖК ПОСИЛАНЬ
1. Полiщук РД.С., Дорожовець М.М., Яцук В.О., та iн. Метрологiя та вимiрювальна технiка: Пiдручник / РД.С.Полiщук, М.М.Дорожовець, В.О.Яцук, В.М.Ванько, Т.Г.Бойко; За ред. проф. РД.С.Полiщука. тАУ Львiв: Видавництво тАЬБескид БiттАЭ, 2003.
2. ДСТУ 2681-94. Метрологiя. Термiни та визначення. тАУ К.: Держстандарт Украiни, 1994.
3. Володарський РД.Т., Кухарчук В.В, Поджаренко В.О., Сердюк Г.Б. Метрологiчне забезпечення вимiрювань i контролю. Навчальний посiбник. тАУ Вiнниця ВДТУ, 2001.
4. Кухарчук В.В., Кучерук В.Ю., Долгополов В.П., Грумiнська Л.В. Метрологiя та вимiрювальна технiка. Навчальний посiбник. тАУ Вiнниця: УНРЖВЕРСУМ-Вiнниця, 2004.
Додаток А
РозвтАЩязок диференцiйного рiвняння в пакетi Maple 7
x(t):=cos(t); ode1:=1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+3.1*sin(2.1*t)=
=0.5*x(t);
![]()
![]()
dsolve({ode1,y(0)=0,D(y)(0)=0});

y1(t) := 34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)-
-55/746*sin(t)-125/746*cos(t)+103507151/432161530*exp(-25/11*t)-
-41/105;

with(plots):plot({cos(t),y1(t)},t=0.50);
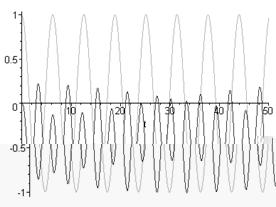
dsolve({1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+
+3.1*sin(2.1*t)=0.5*Heaviside(t),y(0)=0, D(y)(0)=0});
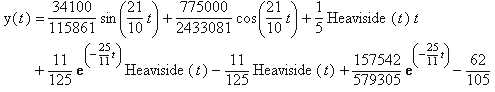
y2(t) := 34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)+
+1/5*Heaviside(t)*t+11/125*exp(-25/11*t)*Heaviside(t)-
-11/125*Heaviside(t)+157542/579305*exp(-25/11*t)-62/105;

plot({y2(t)},t=0.20);
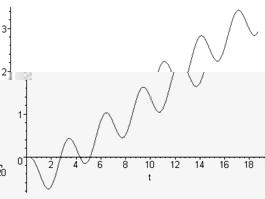
dsolve({1.1*diff(diff(y(t),t),t)+2.5*diff(y(t),t)+
+3.1*sin(2.1*t)=0.5*Dirac(t),y(0)=0, D(y)(0)=0});
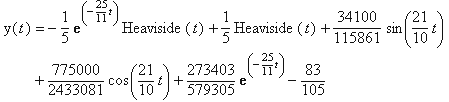
y3(t) := -1/5*exp(-25/11*t)*Heaviside(t)+1/5*Heaviside(t)+
+34100/115861*sin(21/10*t)+775000/2433081*cos(21/10*t)+
+273403/579305*exp(-25/11*t)-83/105;
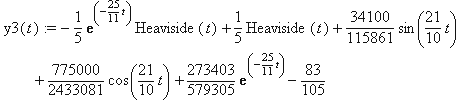
plot({y3(t)},t=0.20);
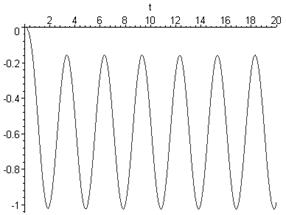
S(f):=(4.41-(2*Pi*f)^2)/(2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51-
-5*sqrt(-1)*(2*Pi*f)^3+22.05*2*Pi*f*sqrt(-1));
![]()
S(f):=(4.41-(2*Pi*f)^2)*((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51) +
sqrt(-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))/ ((2.2*(2*Pi*f)^4-
-9.3*(2*Pi*f)^2+6.51)^2 -( sqrt(-1)*(5*(2*Pi*f)^3+
+22.05*2*Pi*f))^2);
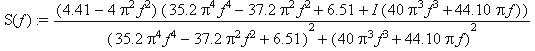
A(f):=(4.41-(2*Pi*f)^2)*(2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+
+6.51) / ((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51)^2 -( sqrt(-
-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))^2);
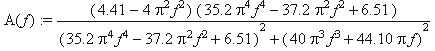
B(f):=(4.41-(2*Pi*f)^2)*(5*(2*Pi*f)^3+
+22.05*2*Pi*f) / ((2.2*(2*Pi*f)^4-9.3*(2*Pi*f)^2+6.51)^2 тАУ
-( sqrt(-1)*(5*(2*Pi*f)^3+22.05*2*Pi*f))^2);

K(f):=sqrt( (A(f))^2+(B(f))^2 );
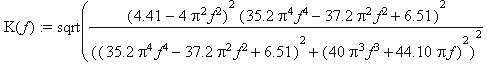
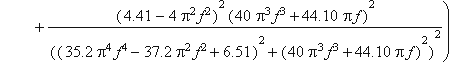
plot(K(f),f=0.1);
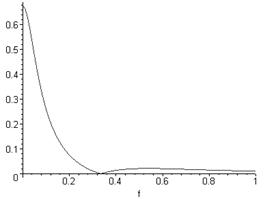
Q(f):=-arctan((B(f)/A(f)));
![]()
plot(Q(f),f=0.1);
Вместе с этим смотрят:
IP-телефония. Особенности цифровой офисной связи