Проектирование системы оптимального корректирующего устройства
1. СИНТЕЗ ЛИНЕЙНОЙ СИСТЕМЫ
1.1 Анализ исходной системы
1.2 Анализ системы с пропорциональным регулятором
1.2.1 Определение коэффициента усиления пропорционального регулятора
1.2.2 Проверка устойчивости замкнутой системы
1.2.3 Определение показателей качества
1.2.4 Анализ системы на соответствие ТЗ
1.3 Синтез регулятора
1.4 Анализ скорректированной системы
1.4.1 Построение частотных характеристик, определение устойчивости системы
1.4.2 Определение частотных ПК, запасов устойчивости, критического коэффициента усиления
1.4.3 Определение оценок прямых ПК
1.4.4 Определение корневых оценок прямых ПК
1.4.5 Оценка точности системы
2. ОТРАБОТКА ТИПОВЫХ ВХОДНЫХ СИГНАЛОВ
2.1 Единичный ступенчатый сигнал
2.1.1 Начальные и конечные значения переходных функций по передаточным функциям системы
2.1.2 Переходные функций системы, прямые ПК
2.1.3 Сравнение начальных и установившихся значений переходных функций
2.1.4 Определим величину Y0 ступенчатого сигнала, при котором система работает в зоне линейности УМ
2.2 Сигнал с постоянной скоростью
2.3. Гармонический сигнал
2.3.1 Определение частоты ω0
2.3.2 Реакция системы на гармонический входной сигнал
2.3.3 Определение амплитудно-фазовых искажений
3. ОБЛАСТЬ УСТОЙЧИВОСТИ
4. АНАЛИЗ СИСТЕМЫ С УЧЕТОМ НЕЛИНЕЙНОСТИ УМ
4.1 Отработка ступенчатых сигналов
4.2 Определение автоколебаний в замкнутой системе
4.3 Отработка гармонических сигналов
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
введение
В курсовой работе рассматривается замкнутая, одномерная, стационарная, непрерывная, следящая система с частично заданной структурой, то есть большинство ее элементов уже выбраны в соответствии с принятым принципом управления, функциональным назначением и условиями согласования с объектом управления. Система является нелинейной, однако анализ проводится как с учетом, так и без учета нелинейностей ее отдельных элементов.
При проектировании системы с частично заданной структурой основной проблемой является синтез линейной системы, т.е. определение параметров корректирующего устройства, обеспечивающего заданные требования к качеству регулирования.
В широком смысле выбор оптимального корректирующего устройства осуществляется на основе требований к массе, габаритным размерам, стоимости и других параметров, определяемых условиями эксплуатации. В более узком смысле, необходимо обеспечить качество системы в установившемся и в переходном режимах.
Для рассматриваемой системы, кроме обеспечения заданных требований, необходимо выполнить некоторые ограничения:
- ограничения на коэффициент усиления: его увеличение может неблагоприятно сказаться на возрастании влияния помех, что вызывает проблемы при конструировании и наладке системы;
- ограничения на положение высокочастотных асимптот логарифмической амплитудной характеристики: желательно иметь больший наклон асимптот;
- ограничения на порядок модели корректирующего устройства: не выше второго порядка;
- ограничения на величину частоты среза: ее уменьшение неблагоприятно сказывается на быстродействии системы.
1. СИНТЕЗ ЛИНЕЙНОЙ СИСТЕМЫ
1.1 Анализ исходной системы
Составим функциональную схему замкнутой системы. Система содержит последовательно включенные в прямой цепи: усилитель мощности (УМ) и объект управления (ОУ), в цепи обратной связи: датчик обратной связи (ДОС), связанный с ОУ при помощи кинематической связи (КС). Схема показана на рис. 1.1.
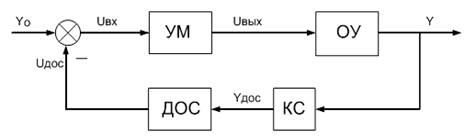
Рис. 1.1. Функциональная схема исходной системы
Составим структурную схему исходной системы. УМ предполагается безынерционным, но с ограниченной зоной линейности 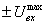 . В КС между ОУ и ДОС присутствует люфт (зазор) величиной 2∆. Схема изображена на рис. 1.2.
. В КС между ОУ и ДОС присутствует люфт (зазор) величиной 2∆. Схема изображена на рис. 1.2.
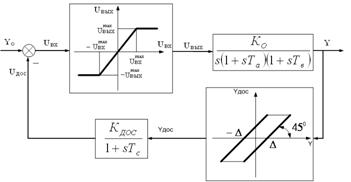
Рис. 1.2. Структурная схема исходной системы
Проведем линеаризацию исходной системы. Для этого необходимо пренебречь наличием нелинейных эффектов, то есть считать, что УМ имеет неограниченную зону нелинейности, зазор (люфт) в КС отсутствует, а коэффициент передачи равен единице.
Рассчитаем коэффициент УМ:
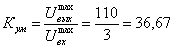 .
.
В техническом задании (ТЗ) коэффициент передачи датчика угла 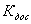 Ваимеет размерность В/град. Для согласования размерностей в системе необходимо привести
Ваимеет размерность В/град. Для согласования размерностей в системе необходимо привести 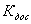 Вак размерности В/рад. Для этого введем коэффициент согласования
Вак размерности В/рад. Для этого введем коэффициент согласования 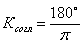 Ваград/рад:
Ваград/рад:
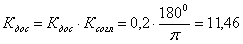 ВаВ/рад.
ВаВ/рад.
Структурная схема линеаризованной системы в общем виде изображена на рис. 1.3, с числовыми параметрами на рис. 1.4.
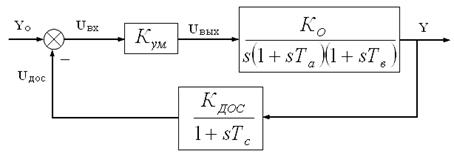
Рис. 1.3. Структурная схема линеаризованной системы в общем виде
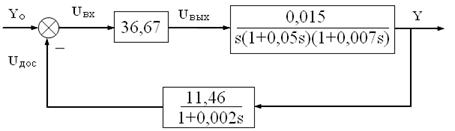
Рис. 1.4. Структурная схема линеаризованной системы с числовыми параметрами
Передаточная функция разомкнутой системы (ПФ РС):
 .
.
Проведем анализ устойчивости исходной системы по алгебраическому критерию Гурвица [1, Вз6.2]. Для этого запишем характеристическое уравнение замкнутой системы (ХУ ЗС):
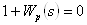 ,
,
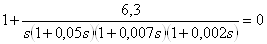 ,
,
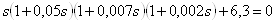 ,
,
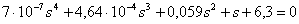 ,
,
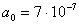 ;
; 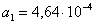 ;
; 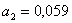 ;
; 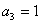 ;
; 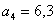 .
.
Все коэффициенты ХУ ЗС положительны (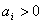 ), следовательно, необходимое условие устойчивости выполняется.
), следовательно, необходимое условие устойчивости выполняется.
Проверим достаточное условие устойчивости. Для этого все n определителей Гурвица, где n тАУ порядок системы, должны быть положительны. Составим определители для системы четвертого порядка:
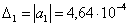 ,
,
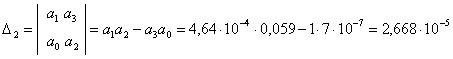 ,
, 
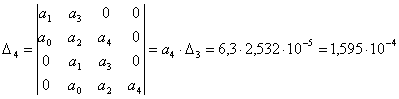 .
.
Все определители положительны, следовательно, исходная система устойчива.
Проведем анализ системы на соответствие требованиям ТЗ.
1. Для определения амплитудно-фазовых искажений запишем передаточную функцию замкнутой системы (ПФ ЗС) по выходу ДОС, а также выражения для логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ):
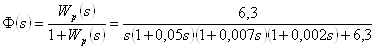 ,
,
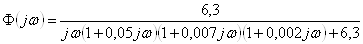 ,
,
 ,
,
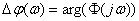 .
.
Заданные в ТЗ и рассчитанные значения амплитудно-фазовых искажений приведены в табл. 1.1.
Таблица 1.1
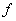 , Гц , Гц
| 0тАж0,15 | 0,15тАж0,5 | 0,5тАж 1,3 |
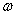 , с-1 , с-1
| 0,942 | 3,142 | 8,168 |
| Заданные значения | 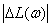 , дБ , дБ
| 0,1 | 0,4 | 2,5 |
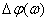 , град , град
| 3 | 5 | 16 |
| Расчетные значения | 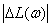 , дБ , дБ
| 0,025 | 0,294 | 2,354 |
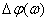 , град , град
| 8,57 | 28,68 | 73,35 |
Вместе с этим смотрят:
GPS-навигация
GPS-прийомник авиационный
IP-телефония и видеосвязь
IP-телефония. Особенности цифровой офисной связи
РЖсторiя диктофону