Элементы биомеханики
Элементы биомеханики
План
1. Деформация и её виды
2. Основные характеристики деформации. Закон Гука для упругой деформации
3. Реологическое моделирование биотканей
4. Механические свойства биотканей
4.1 Механические свойства костной ткани
4.2 Механические свойства ткани кровеносных сосудов
1. Деформация и её виды
деформация биоткань механический костный сосуд
Деформацией называется изменение взаимного расположения точек тела, которое сопровождается изменением его форм и размеров, обусловленное действием внешних сил на тело.
Виды деформации:
1. Упругая тАУ полностью исчезает после прекращения действия внешних сил.
2. Пластическая (остаточная) тАУ остается после прекращения действия внешних сил.
3. Упруго-пластическая тАУ неполное исчезновение деформации.
4. Вязко-упругая тАУ сочетание вязкого течения и эластичности.
В свою очередь упругие деформации бывают следующих видов:
а) деформация растяжения или сжатия происходит под действием сил, действующих в направлении оси тела:
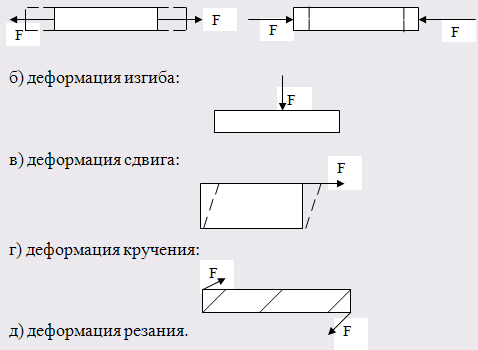
2. Основные характеристики деформации
Деформация растяжения (сжатия) возникает в теле при действии силы, направленной вдоль его оси.
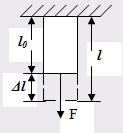
где l0 тАУ исходный линейный размер тела.
Δl тАУ удлинение тела
[l] - м
Деформация ε (относительное удлинение) определяется по формуле
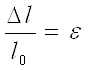Ваε тАУ безразмерная величина.
Мерой сил, стремящихся вернуть атомы или ионы в первоначальное положение является механическое напряжение σ. При деформации растяжения напряжение σ можно определить отношением внешней силы к площади поперечного сечения тела:
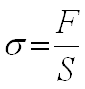
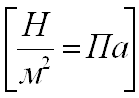
Упругая деформация подчиняется закону Гука:
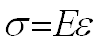
где Е тАУ модуль нормальной упругости (модуль Юнга тАУ это механическое
напряжение, которое возникает в материале при увеличении
первоначальной длины тела в два раза).
Если живые ткани мало деформируется, то в них целесообразно определять не модуль Юнга, а коэффициент жесткости. Жесткость характеризует способность физической среды сопротивляться образованию деформаций.
Представим экспериментальную кривую растяжения:
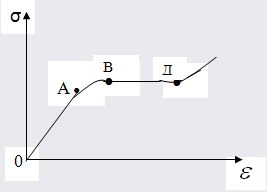
ОА тАУ упругая деформация, подчиняющася закону Гука. Точка В тАУ это предел упругости т.е. максимальное напряжение Вапри котором ещё не имеет место деформация, остающаяся в теле после снятия напряжения. ВД тАУ текучесть (напряжение, начиная с которого деформация возрастает без увеличения напряжения).
Упругость, свойственную полимерам называют эластичностью.
Всякий обрзец, подвергнутый сжатию или растяжению вдоль его оси, деформируется так же и в перпендикулярном направлении.
Абсолютное значение отношения поперечной деформации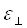 
Вак продольной деформации 
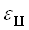Ваобразца называется коэффициентом поперечной деформации или коэффициентом Пуассона и обозначается:
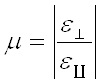Ва(безразмерная величина)
Для несжимаемых материалов (вязкотекучие пасты; резины) μ=0,5; для большинства металлов μ≈0,3.
Величина коэффициента Пуассона при растяжении и сжатии одна и та же. Таким образом, определяя коэффициент Пуассона можно судить о сжимаемости материала.
3. Реологическое моделирование биотканей
Реология тАУ это наука о деформациях и текучести вещества.
Упругие и вязкие свойства тел легко моделируются.
Представим некоторые реологические модели.
а) Модель упругого тела тАУ это упругая пружина.
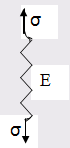
Напряжение, возникающее в пружине, определяется законом Гука:
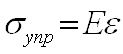
Если упругие свойства материала одинаковы во всех направлениях, то он называется изотропным, если эти свойства неодинаковы тАУ анизотропным.
б) Модель вязкой жидкости - это жидкость, находящаяся в цилиндре с поршнем, неплотно прилегающим к его стенкам или: - это поршень с отверстиями, который движется в цилиндре с жидкостью.
Для этой модели характерна прямо пропорциональная зависимость между возникающим напряжением σ и скоростью деформации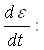 
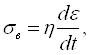
где η тАУ коэффициент динамической вязкости.
в) Реологическая модель Максвелла представляет собой последовательно соединенные упругий и вязкий элементы.
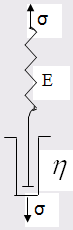
Работа отдельных элементов зависит от скорости нагрузки общего элемента.
Для упругой деформации выполняется закон Гука:
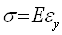
Откуда
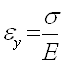
Скорость упругой деформации будет:
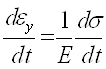Ва(1)
Для вязкой деформации:
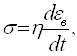
тогда скорость вязкой деформации будет:
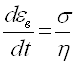Ва(2)
Общая скорость вязко-упругой деформации равна сумме скоростей упругой и вязкой деформаций.
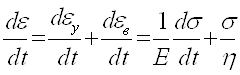Ва(3)
Это есть дифференциальное уравнение модели Максвелла.
Вывод уравнения ползучести биоткани. Если к модели приложить силу, то пружина мгновенно удлиняется, а поршень движется с постоянной скоростью. Таким образом, на данный модели реализуется явление ползучести. Если F=const, то возникающее напряжение σ=const, т.е.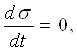 
Ватогда из уравнения (3) получим:
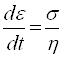, отсюда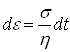 
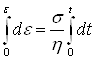
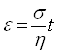
- уравнение ползучести биоткани.
Представим график ползучести:
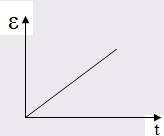
Вывод уравнения релаксации напряжения в биотканях.
Если модель Максвелла растянуть и закрепить, то пружина начнет сокращаться. Со временем будет происходить релаксация, т.е. уменьшение напряжения. Если ε=const, то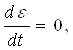 
Ватогда уравнение (3) примет вид:
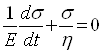
Решаем дифференциальное уравнение:
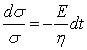
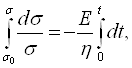
где σ0 тАУ начальное напряжение.
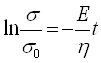
Потенцируем:
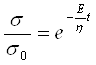
Откуда
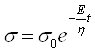
- уравнение релаксации напряжения
Представим график релаксации напряжения.
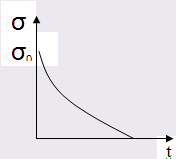
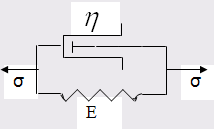
г) Модель Фойгта представляет собой параллельно соединенные упругий и вязкий элементы. Эта модель характерна для полимеров.
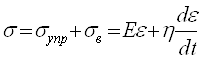
4. Механические свойства биотканей
Под механическими свойствами биотканей понимают две разновидности:
Первая (активная) связана с процессами биологической подвижности: сокращение мышц, рост клеток, движение хромосом в клетках, их деления и т.д. Эти процессы обусловлены химическими процессами и энергетически обеспечиваются АТФ. Другая разновидность - пассивные механические свойства биосистем обусловленные внешними воздействиями.
Биологическая ткань тАУ композиционный материал, образованный объемным сочетанием химически разнородных элементов и обладающий реологическими свойствами, отличающимися от свойств отдельных компонентов биоткани. Основу биотканей составляют коллаген, эластин и связующее вещество.
Механические воздействие на биоткани вызывают в них деформации и напряжения, появляется механическое движение, распространяются волны. Физиологическая реакция на эти факторы зависит от механических свойств биотканей. Знать, как меняются эти реакции и свойства тканей очень важно для профилактики, защиты организма, для применения искусственных тканей и органов, а также для понимания их физиологии и патологии.
В биомеханике все ткани человека подразделяются по плотности и типу пространственной структуры на твердые (кость, эмаль и дентин зубов), мягкие (мышцы, эпителий, эндотелий, соединительная ткань, паренхима), жидкие (кровь, лимфа, ликвор, слюна, сперма).
4.1 Механические свойства костной ткани
Костная ткань тАУ основной материал опорно-двигательной системы. Прочность костной ткани зависит от химического состава, общей структуры, системы внутреннего армирования, количества и прочности компонентов, ориентации основных компонентов по отношению к продольной оси кости, возраста, плотности, индивидуальных условий роста и.т.д.
Компактная костная ткань представляет собой среду с пятью структурными уровнями.
Строение компактной костной ткани по Кнетсу.
| № уровня | Состав уровня |
| 1 | Биополимерная молекула трипоколлагена и неорагнические кристаллы (гидроксилопатит 3Са3(РО4)2Са(ОН)2) |
| 2 | Микрофибриллы коллагена (образованы пятью молекулами трипоколлагена) |
| 3 | Волокно (армирующий компонент) состоит из большого количества микрофибрилл и связанные с ними микрокристаллы. |
| 4 | Ламеллы (наименьший самостоятельный конструкционный элемент) тАУ это тонкие изогнутые пластинки, состоящие из коллагенно-минеральных веществ, объединённых при помощи вяжущего вещества. |
| 5 | Остеоны тАУ образуются вокруг кровеносных сосудов, включающихся в объем кости. Состоят из концентрически расположенных костных ламелл. |
Вместе с этим смотрят:
Бiологiчне рiзноманiття людських рас
Биологические ритмы человека
Биосфера и предельные возможности Земли
Бодрствование - нейрофизиологический процесс человека
Виробництво кормового бiлка