РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Як ми вже знаiмо один i той же лiнiйний оператор в рiзних базисах задаiться рiзними матрицями. Виникаi питання: чи не можна знайти такий базис векторного простору, в якому матриця лiнiйного оператора маi найпростiший вигляд. Таким виглядом буде дiагональний вигляд. До вияснення цього питання ми i приступаiмо.
1. РЖнварiантнi пiдпростори.
Нехай U пiдпростiр векторного простору Vn, а φ тАУ лiнiйний оператор, заданий на просторi Vn.
Означення. Пiдпростiр U векторного простору Vnназиваiться iнварiантним вiдносно лiнiйного оператора φ, якщо образ ![]() φ кожного вектора
φ кожного вектора ![]()
![]() Ваiз U належить цьому пiдпростору U, тобто
Ваiз U належить цьому пiдпростору U, тобто
![]() .
.
Приклади.
1. Розглянемо звичайний тривимiрний простiр V3 i нехай φ тАУ поворот навколо осi OZ. РЖнварiантними пiдпросторами будуть, наприклад, площина XOY i сама вiсь OZ.
2. Розглянемо знову векторний простiр V3 i лiнiйний оператор φ, який полягаi в ортогональному проектуваннi векторного простору V3 на площину XOY. РЖнварiантними пiдпросторами будуть: площина XOY, сама вiсь OZ, всi площини, якi проходять через вiсь OZ i всi прямi площини XOY, якi проходять через початок координат.
3. В будь-якому векторному просторi кожен пiдпростiр iнварiантний вiдносно тотожного i нульового оператора.
4. В будь-якому векторному просторi сам простiр i його пiдпростiр, який складаiться тiльки з нульового вектора, iнварiантнi вiдносно будь-якого лiнiйного оператора.
Доведемо, що перетин i сума пiдпросторiв, iнварiантних вiдносно лiнiйного оператора φ, iнварiантнi вiдносно цього оператора φ.
Нехай пiдпростори U1 i U2 тАУ iнварiантнi вiдносно лiнiйного оператора ![]() , i нехай
, i нехай ![]() .
.![]() ВаТодi
ВаТодi ![]() Ваi
Ваi ![]() , а значить
, а значить ![]() Ваi
Ваi ![]() , тобто
, тобто ![]() . Отже,
. Отже, ![]() - iнварiантний пiдпростiр вiдносно оператора
- iнварiантний пiдпростiр вiдносно оператора ![]() .
.
Нехай ![]() , де
, де ![]() Ваi
Ваi ![]() . Тодi
. Тодi ![]() Ваi
Ваi ![]() ,
, ![]() .
.![]() Отже,
Отже, ![]() ВатАУ iнварiантний пiдпростiр вiдносно оператора
ВатАУ iнварiантний пiдпростiр вiдносно оператора ![]() .
.
Особливу роль вiдiграють одновимiрнi iнварiантнi пiдпростори.
2. Власнi вектори i власнi значення.
Означення. Власним вектором лiнiйного оператора φ називаiться ненульовий вектор ![]() , для якого виконуiться рiвнiсть
, для якого виконуiться рiвнiсть ![]() , де
, де ![]() ВатАУ деяке число, яке називаiться власним значенням лiнiйного оператора, якому вiдповiдаi власний вектор
ВатАУ деяке число, яке називаiться власним значенням лiнiйного оператора, якому вiдповiдаi власний вектор ![]() .
.
Властивостi власних векторiв.
1. Якщо ![]() ВатАУ власний вектор лiнiйного оператора
ВатАУ власний вектор лiнiйного оператора ![]() Ваз власним значенням
Ваз власним значенням ![]() , то вектор
, то вектор ![]() Вапри будь-якому
Вапри будь-якому ![]() Ватакож i власним вектором з тим самим власним значенням
Ватакож i власним вектором з тим самим власним значенням ![]() .
.
2. Якщо ![]() ,
, ![]() ,тАж,
,тАж,![]() ВатАУ власнi вектори лiнiйного оператора
ВатАУ власнi вектори лiнiйного оператора ![]() , якi належать до того самого власного значення
, якi належать до того самого власного значення ![]() , то будь-яка iх
, то будь-яка iх![]() лiнiйна комбiнацiя також буде власним вектором цього оператора з тим самим власним значенням
лiнiйна комбiнацiя також буде власним вектором цього оператора з тим самим власним значенням ![]() .
.
3. Теорема. Власнi вектори, якi вiдповiдають рiзним власним значенням, лiнiйно незалежнi.
Доведення. Нехай ![]() ,
, ![]() ,тАж,
,тАж,![]() ВатАУ власнi вектори лiнiйного оператора
ВатАУ власнi вектори лiнiйного оператора ![]() , якi вiдповiдають рiзним власним значенням
, якi вiдповiдають рiзним власним значенням ![]() , вiдповiдно, тобто
, вiдповiдно, тобто ![]() . Доводимо теорему методом математичноi iндукцii за кiлькiстю векторiв.
. Доводимо теорему методом математичноi iндукцii за кiлькiстю векторiв.
Для ![]() Ватеорема справедлива, бо
Ватеорема справедлива, бо ![]() Ваза означенням, i
Ваза означенням, i ![]() Ватодi i тiльки тодi, коли
Ватодi i тiльки тодi, коли ![]() .
.
Нехай теорема справедлива при ![]() , тобто
, тобто ![]() - лiнiйно незалежнi. Припустимо, що
- лiнiйно незалежнi. Припустимо, що
![]() Ва(1)
Ва(1)
i доведемо, що рiвнiсть (1) виконуiться тодi i тiльки тодi, коли всi ![]() .
.
Подiiмо на рiвнiсть (1) лiнiйним оператором ![]() :
:
![]()
використавши лiнiйнiсть оператора ![]() , одержимо
, одержимо
![]()
звiдси
![]() . (2)
. (2)
Вiднiмемо вiд рiвностi (2) рiвнiсть (1), помножену на ![]() . Одержимо
. Одержимо
![]() . (3)
. (3)
За припущенням iндукцii вектори![]() Валiнiйно незалежнi, тому рiвнiсть (3) виконуiться тодi i тiльки тодi, коли всi коефiцiiнти при
Валiнiйно незалежнi, тому рiвнiсть (3) виконуiться тодi i тiльки тодi, коли всi коефiцiiнти при ![]() Вадорiвнюють нулю. Але за умовою
Вадорiвнюють нулю. Але за умовою ![]() Ва(
Ва(![]() ), а тому
), а тому ![]() .
.
Пiдставивши цi значення ![]() Вау рiвнiсть (1), одержимо
Вау рiвнiсть (1), одержимо ![]() , звiдси
, звiдси ![]() , бо
, бо ![]() . Отже, рiвнiсть (1) виконуiться тодi i тiльки тодi, коли всi
. Отже, рiвнiсть (1) виконуiться тодi i тiльки тодi, коли всi ![]() (
(![]() ) одночасно. Тому
) одночасно. Тому ![]() ВатАУ лiнiйно незалежнi.
ВатАУ лiнiйно незалежнi.
Теорему доведено. Повернемось до питання, як знайти власнi значення i власнi вектори лiнiйного оператора. Для цього нам потрiбно розглянути деякi додатковi поняття.
Характеристична матриця
Нехай дана квадратна матриця
 .
.
Матриця
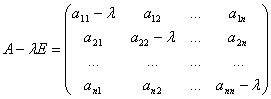
називаiться характеристичною матрицею. Детермiнант цiii матрицi
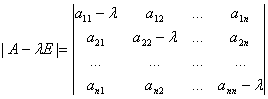
називаiться характеристичним многочленом.
Коренi цього многочлена називаються характеристичними числами.
Теорема. Характеристичнi многочлени подiбних матриць однаковi.
Доведення. Нехай ![]() . Тодi
. Тодi
![]()
Теорема доведена.
Нехай лiнiйний оператор ![]() Вав базисi
Вав базисi ![]() Вавекторного простору
Вавекторного простору ![]() Вазадано матрицею
Вазадано матрицею

i ![]() ВатАУ власний вектор оператора
ВатАУ власний вектор оператора ![]() , який вiдповiдаi власному значенню
, який вiдповiдаi власному значенню ![]() , тобто
, тобто ![]() .
.
Позначимо координати вектора ![]() Вав базисi
Вав базисi ![]() Вачерез
Вачерез ![]() .
.
Тодi з одного боку ![]() , а з другого боку
, а з другого боку ![]() .
.
Тодi 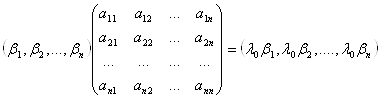
або в розгорнутому виглядi
 Ва(4)
Ва(4)
Звiдси одержимо систему лiнiйних однорiдних рiвнянь
![]()
![]()

![]()
Власний вектор ![]() Ваi ненульовим розвтАЩязком системи (4´). Як вiдомо, однорiдна система лiнiйних рiвнянь з невiдомими маi ненульовi розвтАЩязки тодi i тiльки тодi, коли ii детермiнант дорiвнюi нулю, тобто, коли виконуiться умова
Ваi ненульовим розвтАЩязком системи (4´). Як вiдомо, однорiдна система лiнiйних рiвнянь з невiдомими маi ненульовi розвтАЩязки тодi i тiльки тодi, коли ii детермiнант дорiвнюi нулю, тобто, коли виконуiться умова
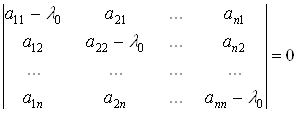
Так як детермiнант при транспонуваннi не змiнюiться, то одержимо рiвняння вiдносно невiдомого ![]()
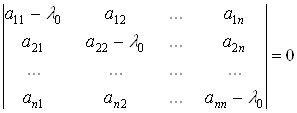 ВаВаВаВаВа (5)
ВаВаВаВаВа (5)
Отже, ми довели теорему: кожне власне значення лiнiйного оператора ![]() , заданого матрицею А, i коренем характеристичного многочлена.
, заданого матрицею А, i коренем характеристичного многочлена.
Провiвши мiркування знизу вверх, одержимо твердження: кожний корiнь характеристичного многочлена лiнiйного оператора ![]() Вабуде його власним значенням.
Вабуде його власним значенням.
В ходi доведення теореми ми одержали схему знаходження власних значень i власних векторiв лiнiйного оператора.
Приклад. Знайти власнi значення i власнi вектори лiнiйного оператора заданого матрицею
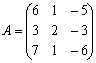
Схема розвтАЩязування:
1. Складаiмо характеристичну матрицю
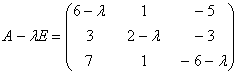 .
.
2. Шукаiмо характеристичний многочлен
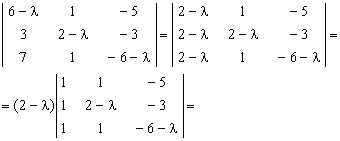
=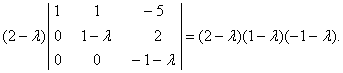
3. РозвтАЩязуiмо характеристичне рiвняння
(2-![]()
![]()
Отже, власними значеннями лiнiйного оператора i числа 1, 2, -1.
4. Для знаходження власних векторiв розвтАЩязуiмо систему рiвнянь
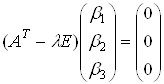 Ватобто
Ватобто  Ва(5)
Ва(5)
а) Шукаiмо власнi вектори, якi вiдповiдають власному значенню ![]() Вапiдставивши у (5) замiсть
Вапiдставивши у (5) замiсть ![]() Ваодиницю:
Ваодиницю:
 Ваабо в розгорнутому виглядi
Ваабо в розгорнутому виглядi
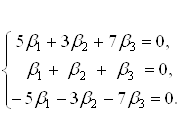
Ранг цiii системи дорiвнюi 2, тому фундаментальна система ii розвтАЩязкiв складаiться з одного розвтАЩязку. Знаходимо його. Злiва залишаiмо змiннi ![]() , а
, а ![]() Ваперенесемо в праву частину i вважаiмо ii вiдомою:
Ваперенесемо в праву частину i вважаiмо ii вiдомою: 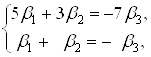 Вазвiдси
Вазвiдси ![]() ВаПокладемо
ВаПокладемо ![]() Ватодi
Ватодi ![]() . Отже, одним iз власних векторiв, якi вiдповiдають власному значенню
. Отже, одним iз власних векторiв, якi вiдповiдають власному значенню ![]() Ваi вектор
Ваi вектор ![]() ВаВсi власнi вектори, якi вiдповiдають цьому значенню мають вигляд
ВаВсi власнi вектори, якi вiдповiдають цьому значенню мають вигляд ![]() , де
, де ![]() -будь-яке дiйсне число, вiдмiнне вiд нуля.
-будь-яке дiйсне число, вiдмiнне вiд нуля.
Самостiйно знайти власнi вектори, якi вiдповiдають власним значенням 2 i ![]() .
.
Весь набiр характеристичних коренiв оператора ![]() Ва(причому кожний корiнь береться з тiiю кратнiстю, яку вiн маi в характеристичному рiвняннi) називаiться спектром лiнiйного оператора.
Ва(причому кожний корiнь береться з тiiю кратнiстю, яку вiн маi в характеристичному рiвняннi) називаiться спектром лiнiйного оператора.
Сукупнiсть власних векторiв оператора ![]() , яким вiдповiдаi одне i те саме власне значення
, яким вiдповiдаi одне i те саме власне значення ![]() , збiгаiться з сукупнiстю всiх ненульових розвтАЩязкiв систем лiнiйних однорiдних рiвнянь.
, збiгаiться з сукупнiстю всiх ненульових розвтАЩязкiв систем лiнiйних однорiдних рiвнянь.
Лiнiйнi оператори з простим спектром
Кажуть, що лiнiйний оператор ![]() Вау тАУ вимiрному просторi
Вау тАУ вимiрному просторi ![]() Ванад полем Р маi простий спектр, якщо всi його характеристичнi коренi рiзнi.
Ванад полем Р маi простий спектр, якщо всi його характеристичнi коренi рiзнi.
Повернемося до питання: чи iснуi базис простору ![]() , в якому лiнiйний оператор
, в якому лiнiйний оператор ![]() Вазадаiться дiагональною матрицею.
Вазадаiться дiагональною матрицею.
Нехай в просторi ![]() Ваiснуi базис, який складаiться з власних векторiв
Ваiснуi базис, який складаiться з власних векторiв ![]() , якi вiдповiдають власним значенням
, якi вiдповiдають власним значенням ![]() , вiдповiдно. Знайдемо матрицю цього оператора в цьому базисi:
, вiдповiдно. Знайдемо матрицю цього оператора в цьому базисi:
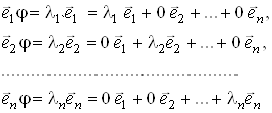

тобто оператор ![]() Вазаданий дiагональною матрицею, причому по дiагоналi стоять власнi значення лiнiйного оператора, якi вiдповiдають власним векторам базису.
Вазаданий дiагональною матрицею, причому по дiагоналi стоять власнi значення лiнiйного оператора, якi вiдповiдають власним векторам базису.
Навпаки. Нехай лiнiйний оператор ![]() Вав деякому базисi
Вав деякому базисi ![]() Вазадаiться довiльною матрицею
Вазадаiться довiльною матрицею  .
.
За означенням матрицi лiнiйного оператора в даному базисi ![]()
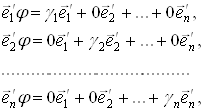 Вазвiдси
Вазвiдси 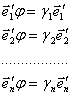 Ватобто вектори базису
Ватобто вектори базису![]() Ваi власними векторами оператора
Ваi власними векторами оператора ![]() Ваз власними значеннями
Ваз власними значеннями ![]() . Таким чином ми довели теорему:
. Таким чином ми довели теорему:
Якщо вектори базису ![]() Ваi власними векторами лiнiйного оператора
Ваi власними векторами лiнiйного оператора ![]() , то в цьому базисi оператор
, то в цьому базисi оператор ![]() Вазадаiться дiагональною матрицею. Навпаки, якщо в деякому базисi матриця оператора
Вазадаiться дiагональною матрицею. Навпаки, якщо в деякому базисi матриця оператора ![]() Ваi дiагональною, то всi вектори цього базису i власними векторами оператора
Ваi дiагональною, то всi вектори цього базису i власними векторами оператора ![]() .
.
Як бачимо, матриця оператора ![]() Вав базисi, що складаiться з власних векторiв цього оператора, маi досить простий вигляд. Саме це i обумовлюi важливiсть ролi власних векторiв, а, отже, i одновимiрних iнварiантних пiдпросторiв при вивченнi лiнiйних операторiв.
Вав базисi, що складаiться з власних векторiв цього оператора, маi досить простий вигляд. Саме це i обумовлюi важливiсть ролi власних векторiв, а, отже, i одновимiрних iнварiантних пiдпросторiв при вивченнi лiнiйних операторiв.
Виникаi питання: як встановити, знаючи матрицю оператора ![]() Вав деякому базисi, чи маi цей оператор власнi вектори, якi утворюють базис простору тобто, чи можна оператор
Вав деякому базисi, чи маi цей оператор власнi вектори, якi утворюють базис простору тобто, чи можна оператор ![]() Вазадати в деякому базисi дiагональною матрицею?
Вазадати в деякому базисi дiагональною матрицею?
Теорема. Якщо лiнiйний оператор ![]() Вамаi простий спектр, то iснуi базис простору
Вамаi простий спектр, то iснуi базис простору ![]() , в якому цей оператор задаiться дiагональною матрицею.
, в якому цей оператор задаiться дiагональною матрицею.
Доведення. Дано: ![]() ВатАУ рiзнi власнi значення оператора
ВатАУ рiзнi власнi значення оператора ![]() , яким вiдповiдають власнi вектори
, яким вiдповiдають власнi вектори ![]() , вiдповiдно, тобто
, вiдповiдно, тобто ![]() , i=1, 2,тАж, n.
, i=1, 2,тАж, n.
Оскiльки ![]()
![]() , i
, i ![]() , то
, то ![]() ВатАУ лiнiйно незалежнi, а значить утворюють базис векторного простору
ВатАУ лiнiйно незалежнi, а значить утворюють базис векторного простору ![]() . В цьому базисi оператор
. В цьому базисi оператор ![]() Вазадаiться дiагональною матрицею
Вазадаiться дiагональною матрицею
вектор ортогональний iнварiантний матриця
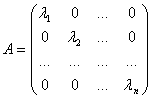 .
.
Теорему доведено.
Зведення матрицi до дiагонального вигляду
Нехай ![]() квадратна матриця порядку
квадратна матриця порядку ![]() з елементами з поля P.
з елементами з поля P.
Вважають, що матриця A зводиться до дiагонального вигляду, якщо iснуi дiагональна матриця, подiбна матрицi A.
Часто трапляiться, що треба знати, чи зводиться квадратна матриця до дiагонального вигляду. На основi попереднiх результатiв можна довести теорему, яка встановлюi достатнi умови звiдностi матрицi до дiагонального вигляду.
Теорема. Кожна квадратна матриця n-го порядку над полем Р, яка маi в полi Р n рiзних характеристичних коренiв, зводиться до дiагонального вигляду, тобто подiбна до дiагональноi матрицi.
Доведення. Дано A тАУ квадратна матриця тАУ гопорядку над полем P. Нехай ![]() - рiзнi характеристичнi коренi матрицi i
- рiзнi характеристичнi коренi матрицi i ![]() Ва(i=1,2,тАж n).
Ва(i=1,2,тАж n).
Розглянемо векторний простiр ![]() Ванад полем P. Матриця A в деякому базисi задаi деякий лiнiйний оператор
Ванад полем P. Матриця A в деякому базисi задаi деякий лiнiйний оператор ![]() . Характеристичнi коренi
. Характеристичнi коренi ![]() Ваi власними значеннями оператора
Ваi власними значеннями оператора ![]() , яким вiдповiдають власнi вектори цього оператора
, яким вiдповiдають власнi вектори цього оператора ![]() ,
, ![]() . За властивiстю власних векторiв, якi вiдповiдають рiзним власним значенням вектори
. За властивiстю власних векторiв, якi вiдповiдають рiзним власним значенням вектори ![]() ВатАУ лiнiйно незалежнi, тому вони утворюють базис простору
ВатАУ лiнiйно незалежнi, тому вони утворюють базис простору ![]() . В цьому базисi матриця лiнiйного оператора
. В цьому базисi матриця лiнiйного оператора ![]() Вамаi вигляд
Вамаi вигляд 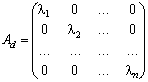 .
.
![]() Ваi A подiбнi, бо вони задають один i той самий оператор
Ваi A подiбнi, бо вони задають один i той самий оператор ![]() Вав рiзних базисах. Дiагональними елементами матрицi
Вав рiзних базисах. Дiагональними елементами матрицi ![]() Ваi характеристично коренi матрицi A.
Ваi характеристично коренi матрицi A.
Знаходження дiагональноi матрицi, подiбноi матрицi A, називаiться зведенням матрицi A до дiагонального вигляду.
Приклад. Звести квадратну матрицю A до дiагонального вигляду, якщо
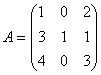 .
.
РозвтАЩязуiмо характеристичне рiвняння: 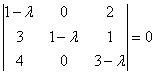
![]() ,
, ![]() . (РозвтАЩязати самостiйно)
. (РозвтАЩязати самостiйно)
Отже, 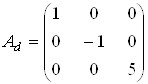 .
.
Вместе с этим смотрят:
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Волоконно-оптические датчики температуры на основе решеток показателя преломления
Время и пространство - идеалистические понятия
Дом и очаг, одежда и пища с точки зрения термодинамики