Математическое моделирование окружающей среды

ГОСКОМВУЗ

Красноярский Государственный Технический Университет

                                                               Кафедра: МО ЭВМ Реферат

Тема: Математическое моделирование окружающей среды.

Выполнил:

Студент группы ВТ26-5

Садовский М.В.

Проверил:

Белолипецкий В.М.

КрасноярсктАЩ 370 лет

Введение:

При изучении любого явления вначале получают качественное описание проблемы. На этапе моделирования качественное представление переходит в количественное. На этом этапе определяют функциональные зависимости между переменными для каждого варианта решения и входных данных выходные данные системы. Построение моделей тАУ процедура неформальная и очень сильно зависит от опыта исследователя, всегда опирается на определённый опытный материал. Модель должна правильно отражать явления, однако этого мало тАУ она должна быть удобной для использования. Поэтому степень детализации модели, форма её представления зависят от исследования.

Изучение и формализация опытного материала тАУ не единственный способ построения математической модели. Важную роль играет получение моделей, описывающих частные явления, из моделей более общих. Сегодня математическое моделирование применяют в различных областях знаний, выработано немало принципов и подходов, носящих достаточно общий характер.

Основная задача научного анализа тАУ выделить реальные движения из множества мысленно допустимых, сформулировать принципы их отбора. Здесь термин тАЬдвижениетАЭ употребляется в широком смысле тАУ изменения вообще, всякое взаимодействие материальных объектов. В различных областях знаний принципы отбора движений разные. Принято различать три уровня организации материи: неживая, живая и мыслящая. На самом нижнем уровне тАУ неживой материи тАУ основными принципами отбора являются законы сохранения вещества, импульса, энергии и т.п. Любое моделирование начинается с выбора основных (фазовых) переменных, с помощью которых записывают законы сохранения.

Законы сохранения не выделяют единственного решения и не исчерпывают всех принципов отбора. Очень важны различные условия (ограничения): граничные, начальные и др.

На уровне живой материи все принципы отбора движений, справедливые для неживой материи, сохраняют свою силу. Поэтому и здесь процесс моделирования начинается с записи законов сохранения. Однако основные переменные оказываются уже иными.

Преимущества математических моделей состоят в том, что они точны и абстрактны, передают информацию логически однозначным образом. Модели точны, поскольку позволяют осуществлять предсказания, которые можно сравнить с реальными данными, поставив эксперимент или проведя необходимые наблюдения.

Модели абстрактны, так как символическая логика математики извлекает те и только те элементы, которые важны для дедуктивной логики рассуждения, исключая все посторонние значения.

Недостатки математических моделей заключаются часто в сложности математического аппарата. Возникают трудности перевода результатов с языка математики на язык реальной жизни. Пожалуй, самый большой недостаток математической модели связан с тем искажением, которое можно привнести в саму проблему, упорно отстаивая конкретную модель,  даже если в действительности она не соответствует фактам, а также с теми трудностями, которые возникают иногда при необходимости отказаться от модели, оказавшейся неперспективной. Математическое моделирование настолько увлекательное занятие, что тАЬмодельерутАЭ очень легко отойти от реальности и увлечься применением математических языков к абстрактным явлениям. Именно поэтому следует помнить, что моделирование в прикладной математике тАУ это лишь один из этапов широкой стратегии исследования.

Моделирование водных экосистем:

Научно-технический прогресс, развитие сельского хозяйства, урбанизация привели к загрязнению природных вод. Проблема загрязнения вод приобрела глобальный характер. В настоящее время выделяют химическое, физическое, биологическое, тепловое, радиоактивное типы загрязнений.

Загрязняющие вещества, в зависимости от типа источника загрязнения, разными путями попадают в водную среду. Они могут поступать из атмосферы; могут быть смыты склоновым стоком с сельскохозяйственных полей и угодий в подземные и речные воды; загрязнение также может быть бактериальным в результате развития и отмирания водной растительности. Поступление загрязняющих веществ в водоём может происходить непрерывно (по времени) или в результате массового сброса, в виде точечных или распределённых в пространстве источников.

При имитационном моделировании качества воды необходимо совместное описание гидрофизических и химико-биологических процессов. Задача моделирования заключается в том, чтобы научиться предвидеть, возможно, более отдалённые последствия вмешательства человека в установившийся в природе круговорот веществ и уметь нейтрализовать нежелательные результаты.

Под экосистемой понимают единый природно-антропогенный комплекс, образованный живыми организмами и средой их обитания, в котором экологические компоненты связаны между собой причинно-следственными связями, обменом веществ и распределением потока энергии. Водная экосистема является элементом системы  более высокого порядка тАУ биосферы. Водоём тАУ открытая система, связанная с окружающей средой входными и выходными данными.

Остановимся на описании водных потоков и в качестве примера Упрощённое уравнение для расчёта температурного режима реки. Температурный режим водных потоков описывается уравнением теплопроводности Фурье тАУКирхгофа:

,

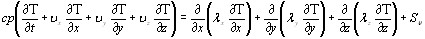где x, y, z тАУ декартовы координаты, t тАУ время, T тАУ температура, 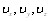-  составляющие вектора скорости, с - удельная теплоёмкость воды, p - плотность среды, 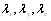- коэффициенты теплопроводности, Sv -  внутренние источники тепла. Для водных потоков в руслах рек и каналов обычно принимают x-овую и z-овую  составляющие вектора скорости равными нулю и  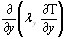тоже равным нулю.

Математическое моделирование глобального развития:

В настоящее время проблема тАЬЧеловек и среда его обитаниятАЭ широко обсуждается во всём мире. Рост населения, истощение природных ресурсов, отрицательные воздействия человека на окружающую среду, нехватка продуктов питания в некоторых развивающихся странах тАУ вот основные аспекты этой проблемы. В условиях научно-технической революции воздействие человека на окружающую его среду приобрело масштабы, которые можно сравнить с природными процессами. Возникла реальная угроза необратимых отрицательных последствий. Современные социально-экономические процессы взаимодействия человека и окружающей среды настолько сложны и масштабны, что нельзя пассивно надеяться на их стихийную адаптацию в желательном направлении. Возникает задача тАУ изучить действие всех в совокупности факторов, обуславливающих развитие человечества, найти пути сознательного управления этим развитием.

В этих условиях важным инструментом анализа управления развитием сложных систем становятся методы математического моделирования. Методологической базой комплексного исследования наиболее важных сторон развития человеческого общества является системный анализ. Системный анализ тАУ это прикладная дисциплина, занимающаяся решением конкретных проблем, возникающих в процессе проектирования и анализа сложных технических, биологических, экономических  и прочих систем.

Глобальные модели Форрестера и Мидоуза.

Первая попытка формализовать описание экологических процессов была принята в 1971 г. американским исследователем Дж. Форрестером. В своей книге тАЬМировая динамикатАЭ Форрестер предложил некоторый вариант модели экономического развития, содержащий лишь два экологических параметра: численность населения и загрязнение среды. Модель позволила оценивать взаимное влияние этих параметров, с одной стороны, и темпов экономического развития тАУ с другой. Хотя, как писал сам Форрестер, основная задача его книги была чисто методической, а модель носила учебный характер, роль его работы в развитии исследований глобального характера трудно переоценить. Впервые была продемонстрирована принципиальная возможность объединить производственные, социальные и экологические процессы одним формализмом. Через год после тАЬМировой динамикитАЭ вышла в свет книга тАЬПределы ростатАЭ, написанная группой ученых под руководством Д. Мидоуза. Модель Мидоуза тАУ тАЬМир - 3тАЭ тАУ представляет собой систему нелинейных дифференциальных уравнений, описывающих динамику взаимодействия таких секторов, как народонаселение, промышленность, сельское хозяйство, не возобновляемые природные процессы, загрязнение среды и др. Целью их работы было выявление общих качественных тенденций процесса взаимосвязанного изменения основных переменных системы, анализ чувствительности результатов по отношению к различным заложенным в модель предположениям.

Работы Форрестера и Мидоуза вызвали широкий отклик в мировой литературе. Принципиальным недостатком математических моделей тАЬМир-2тАЭ и тАЬМир-3тАЭ являлось то, что модели не отражали возможности сознательного воздействия человека на процесс развития. Но следует отметить определённое положительное значение указанных работ. Впервые были системно проанализированы некоторые глобальные экономические. Демографические и экологические процессы.

Проект тАЬСтратегия выживаниятАЭ Месаровича тАУ Пестеля.

Следующим этапом в работах по глобальному моделированию явился проект тАЬСтратегия выживаниятАЭ, который возглавил М. Месарович (США) и Э. Пестель (ФРГ). Критикуя модель тАЬМир-3тАЭ как тАЬмеханическуютАЭ, Месарович и Пестель выдвигают задачу построения тАЬкибернетическойтАЭ модели мира. Основные принципы её построения могут быть сформулированы в трёх тезисах:

1. Модель, отражающая сложные процессы взаимодействия человека с окружающей средой, должна основываться на теории многоуровневых  иерархических систем.
2. Модель должна быть управляемой, т.е. включать в себя процесс принятия решений, что позволяет учесть возможность сознательного воздействия человека на развитие мировой системы. Для этого необходимо обеспечить работу в режиме диалога между исследователем модели и ЭВМ.
3. Мир следует рассматривать не как единое однородное целое, а как систему взаимодействующих регионов, различающихся уровнем развития, населенностью и т.п.

В модели Месаровича тАУ Пестеля (М-П-модель) все страны мира, в соответствии с их социально-экономическими структурами и уровнями развития, объединены в 10 регионов; каждый регион описывается системой региональных подмоделей, их структура тАУ одна и та же для всех регионов, отличие тАУ в начальных данных и значениях параметров. Связь регионов осуществляется через миграцию населения, импорт и экспорт продукции.

Латиноамериканская модель глобального развития.

В 1974 г. группа аргентинских учёных во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью глобального развития. Предпосылки для выполнения работы при обсуждении модели тАЬМир-3тАЭ послужил тезис о том, что основные преграды на пути гармонического развития человечества заключаещися главным образом в неравномерном распределении богатства между различными странами.

В модели Эрреры за основную цель развития человеческого общества принято достижение удовлетворительных условий жизни всеми странами мира, а не просто рост материального потребления. Под удовлетворительными условиями понимаются некоторые достаточно высокие уровни медицинского обслуживания, образования, обеспеченности питанием и жильём.

Список литературы:

1. Математическое моделирование в задачах охраны окружающей среды. Белолипецкий В.М. Шокин Ю.И.
2. Дополнительные главы естествознания. Применения законов сохранения в математическом моделировании. Белолипецкий В.М., Дулов В.Г.
3. Математическое моделирование окружающей среды. Белолипецкий В.М.

Вместе с этим смотрят:

Математическое моделирование полета лыжника
Математическое моделирование системных элементов
Математическое программирование
Матричный анализ