Структура исчисления предикатов. Построение логического вывода
Язык, логика и исчисление предикатов
Введение
Приступая к изучению языка логики предикатов (сокращенно тАФ ЯЛП), полезно вспомнить основные особенности языков этого типа В ЯЛП явно должны быть представляемы субъектно-предикатные структуры высказываний, от которых происхоВндило отвлечение при введении пропозициональных символов. Выражаемыми должны быть, например, высказывания видов. Влa обладает свойством РВ», Вла и b находятся в отношеВннии РВ», ВлДля всякого предмета из некоторого множества S верно, что он обладает свойством РВ», ВлДля всякого предмета из множества S существует предмет этого множества такой, что эти предметы находятся в отношении RВ», ВлЕсли неверно, что всякие два предмета некоторого множества находятся в отношении R, то существуют по крайней мере два предмета этого множества, не находящиеся в этом отношенииВ», ВлЕсли во множестве S существует предмет х, который находится в отВнношении R с любым предметом у этого множества, то для всякого предмета у того же множества существует предмет х такой, что последний находится в отношении R к первомуВ» и т. п.
Ясно, во-первых, что для выражения таких утверждений у нас нет средств в языке логики высказываний. Ясно и то, что для выражения подобных высказываний в ЯЛП мы долВнжны иметь в числе его исходных символов общие имена предметов; аналогами последних в ЯЛП будут предметные переменные х, у, z, а также они же с числовыми индексами xтВБ,xтВВ, .. и т.д. Потребность в общих именах при употреблеВнний ЯЛП сохранится лишь для описания областей возможВнных значений этих переменных, что относится уже не к саВнмому языку, а к метаязыку. Нужны также знаки свойств и отношений. Для выражения высказываний вида ВлОбъем тела а больше объема тела bВ» или ВлСинус х меньше косинуса yВ» и т. п. необходимы, конечно, и предметные функторы. ВпроВнчем, перечислим систематически основные типы выражений описываемого языка, каковыми являются: исходные симвоВнлы, термы и формулы. Описание этих выражений составит синтаксис ЯЛП.
СИНТАКСИС ЯЗЫКА ЛОГИКИ ПРЕДИКАТОВ (ИСХОДНЫЕ СИМВОЛЫ, ТЕРМЫ, ФОРМУЛЫ)
I. Исходные символы языка.
1. Предметные переменные х, у, z, а также х с числовыми индексами:
(бесконечное счетное множество).
2. Предметные константы (аналоги собственных имен есВнтественного языка): (также бесконечное счетное множество).
3. Знаки свойств и отношений различных местностей тАФ предикатные символы, или предикаторы:
PВ№, Q В№, RВ№, SВ№, ..;
Р2, Q2, R2, SВІ , ..;
тАжтАжтАжтАжтАжтАжтАж.
PтБї,QтБї,RтБї,SтБї
и возможно эти символы с нижними индексами:
PВ№тВБ , PВ№тВВ, PВ№тВГ, тАж
PВІтВБ , PВІтВВ, PВІтВГ, тАж и т.д.
(верхние индексы указывают на местность предикатора, ниВнжние индексы используются для расширения множества предикаторов той или иной местности; количество предикатВнных символов той или иной местности вводится в зависимоВнсти от предназначения языка. Однако, поскольку речь идет о языке логики предикатов, должен быть введен, по крайней мере один предикатный символ).
4. Знаки предметных функций различных местностей (предметные функторы):
fВ№тВБ , fВ№тВВ, тАж
fВІтВБ ,fВІтВВ , тАж
тАжтАжтАжтАж.
fтБїтВБ , fтБїтВВ, тАж
(число функциональных символов той или иной местности зависит также от предназначения языка, возможно отсутВнствие символов этого рода вообще).
5. Логические константы: тКГ,&,∀,тИГ,тИи,Вм соответственВнно тАФ импликация, конъюнкция, квантор общности, квантор существования, дизъюнкция и отрицание. (Зачастую ввоВндят лишь некоторые из этих символов. Из кванторов достаВнточны только тИА или тИГ, из остальных, называемых логическиВнми связками, достаточно : тКГ и Вм, или тИи и Вм , или & и Вм . Другие константы, как, впрочем, и другие знаки, могут ввоВндиться по определению.)
6. Технические знаки: (- левая скобка, )-правая скобка, ,- запятая.
Предметные константы, предикаторы, предметные функВнторы и предметные переменные называют дескриптивными терминами языка, при этом три первых категории (в отличие от предметных переменных) суть тАФ дескриптивные постоянВнные данного языка.
II. Термы. Выражения этого типа являются аналогами имен естественного языка.
Определение: а) любая предметная переменная и предметная константа есть терм; б) если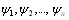 
есть терВнмы и fВётБї есть n-местный предметный функтор, то fВётБї (
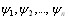есть терм; в) ничто, кроме указанного в пунктах а) и б), не есть терм.
III. формулы. В числе этих выражений имеются аналоги повествовательных предложений естественного языка, а такВнже высказывательные формы тАФ предикаты, представляющие собой особую семантическую категорию, которая не выделяется, тАФ по крайней мере, явным образом тАФ в естественном языке.
Определение: а) если 
термы и PВётБї n-местВнный предикатор, то PВётБї (
) есть формула (атомарная);
б) если А и В тАФ формулы, то (АтКГВ), (А&В), (AvB), ВмA тАФ формулы; в) если х есть предметная переменная и А тАФ форВнмула, то тИА x A и тИГ x A тАФ формулы; г) ничто, кроме указанноВнго в пунктах а) тАФ в), не есть формула.
Договоримся в дальнейшем опускать, когда это удобно, внешние скобки в отдельно взятых формулах; например, вместо (А & В) писать просто
А &В.
Использованные в определениях терма и формулы симВнволы 
и fВётБї, PВётБї, A, B, x (и в дальнейшем возможно xтВБ, x тВВ и т. д.) тАФ знаки метаязыка называемые также синВнтаксическими переменными, возможными знаВнчениями которых являются выражения соответствующей каВнтегории описываемого (объектного) языка.
Формулы А и В, встречающиеся в пунктах б) и в), назыВнваются подформулами указанных здесь формул.
Введенные понятия исходного символа, терма и формулы языка являются эффективными (иначе: рекурсивными). ПоВнследнее означает, что имеется точный способ, с помощью которого всегда можно определить, относится ли некоторый символ к числу исходных символов языка, а для каждой последовательности исходных символов можем определить, представляет ли она терм или формулу. Для термов и формул такой способ заключен в их индуктивных определениях. Так, в каждой формуле, содержащей логические константы (знаки логических операций), имеется главная, или, что то же, последняя, в построении формулы операции. Выделив ее, мы выделяем тем самым собственные подформулы этой формулы. В последних снова выделяем главную операцию и так далее, пока не дойдем до какой-либо атомарной формуВнлы. Если в процессе такого анализа исходного выражения в какой-либо части его, не являющейся атомарной формулой, нельзя выделить знак главной операции, то эта часть не явВнляется формулой, а следовательно, таковой не является все выражение. Возможность распознавания атомарных формул среди последовательностей символов является очевидной. (При констатации эффективности введенных понятий подразумевается так называемая абстракция отождествления согласно которой все различные случаи употребления некотоВнрого символа, например а, рассматриваются как различные экземпляры, одного и того же символа, и предполагается, что мы умеем узнавать символ, несмотря на некоторые, всегда имеющиеся различия в его написаниях.)
СВОБОДНЫЕ И СВЯЗАННЫЕ ВХОЖДЕНИЯ ПЕРЕМЕНЫХ В ФОРМУЛЫ
Каждый случай, когда в последовательности знаков, предВнставляющей собой формулу А, встречается предметная переВнменная x, называется вхождением этой переменной; каждое вхождение в формулу А предметной переменной x в часть вида тИАx В или тИГ х В, называется связанным. ПодВнформула В формул указанного вида называется областью действия соответственно квантора общности тИА и квантора существования тИГ с переменной x. Связанным является вхождение переменной, стоящей непосредственно за квантором, и каждое вхождение ее в область действия квантора. Всякое вхождение х в отличие от указанного, наВнзывается свободным. Переменная х, имеющая связанные вхождения и формулу А, называется связанной в этой формуле; переменная, имеющая свободные вхождения в формулу А, называется свободной в этой формуле.
Обратим внимание на то, что согласно определению свободной и связанной переменной одна и та же переменная в одной и той же формуле может быть свободной и связанной. Такова, например, переменная xтВБ в формуле тИА xтВБ PВ№(xтВБ) тИи QВІ(xтВБ, xтВВ); переменная xтВВ
является здесь свободВнной, но не связанной. Мы рассматриваем здесь только такие термы, в которых все переменные могут иметь лишь свободВнные вхождения, и, значит, являются свободными переменныВнми. Формула и терм, не содержащие свободных переменных, называются соответственно замкнутой формулой и замкнутым т е р м о м (очевидно, что для рассматВнриваемых здесь термов, если терм замкнут, то он вообще не содержит переменных).
СЕМАНТИКА ЯЗЫКА ЛОГИКИ ПРЕДИКАТОВ
Семантику языка, как мы видели при анализе естественного языка, составляет совокупность предметных значений и смысловых содержаний его выражений. Но в данном случае, поскольку речь идет не об анализе уже имеющегося языка, а о построении тАФ в данном случае логического формализованного языка тАФто семантикой называют совокупность правил приписывания значений выражениям этого языка. Точнее говоря, здесь даже не ставится задача построения какого-то определенного языка. Создается лишь некоторая схема языВнка определенного типа, в данном случае так называемой классической логики предикатов первого порядка. Этот тип языка отличается от языков других типов, даже языков с тем же синтаксисом (например, языка интуиционистской логики предикатов, определенной системы релевантной логики) своей семантикой. Приписывание значений отдельным выражениям языка, составляющим дескриптивным терминам, употребляемым при построении формул, осуществляетВнся лишь в составе тех или иных формул и при этом различно от случая к случаю в зависимости от характера решаемых логических задач, (например, при переводе каких то высказываний с естественного языка на данный формализованВнный, при анализе логических отношений между формулами данного языка, при аксиоматизации некоторых теорий, а именно при формулировке их аксиом в языке данного типа). Совокупность всех правил приписывания значений выражеВнниям языка разбивается на следующие три группы (I,II,III).
I. Правила определения (задания) возможных значений предметных переменных и правила приписывания предметВнных значений дескриптивным постоянным в составе расВнсматриваемых в том или ином случае формултАФинтерпретаВнция выражений языка. II. Правила приписывания значений свободным переменным в составе тех или иных рассматриВнваемых формулу. III. Правила приписывания истинностных значений интерпретированным формулам, не содержащим свободных переменных. I. Интерпретация состоит, во-первых, в выборе некотороВнго непустого множества D индивидов, предметов того или иного типа, к которым могут относиться образуемые из тех или иных формул языка высказывания. Индивиды тАФ любые предметы в широком смысле этого слова, структура которых не учитывается, и которые можно отличать друг от друга. В качестве такой области D можно взять множество людей, растений, городов, чисел и т. д.; возможно, также объединеВнние в одной области множеств различных предметов, наприВнмер, людей, городов, домов (положим, для выражения выскаВнзываний о местах жительства людей). Но при этом все различные предметы, рассматриваются именно как индивиды. Область D тАФ это область возможных значений предметных переменных символы предметных переменных х, у, z, станоВнвятся именно переменными лишь при указании области их возможных значений. Предполагается, что на области D определено некоторое множество свойств, отношений и характеристик предметно-функционального типа (то есть возможных значений предикаторов и предметных функторов).
Второй момент интерпретации языка состоит в задании некоторой функции φ
(интерпретационная функция) приписывания значений дескриптивным постоянным (предметным константам, предикаторам, предметным функторам опять-таки в составе рассматриваемых формул). Задание φ
в кажВндом конкретном случае представляет собой просто указание на то, какие значения должны быть приписаны упомянутым исходным символам языка в составе рассматриваемых формул. При этом предметным константам (простые постоянные термы) приписываются в качестве предметных значений определенные предметы из заданной области D. ПредикатноВнму (n-местному) символу PВётБї при n =1 в качестве значения приписываются некоторые свойства а при n > 1 тАФ n-местное отношение (между предметами В). Например, если область D есть множество целых положительных чисел, то предикатВнному символу PВ№тВБ можно приписать в качестве значения свойство ВлчетноВ», а предикатору PВІтВБ отношение ВлбольшеВ» или ВлменьшеВ». Предметному функтору fтБїтВБ в качестве предВнметного значения функция φ
приписывает какую-нибудь n-местную предметную функцию, определенную на облаВнсти D. Например, для области чисел таковыми могут быть сиВннус, косинус (одноместные функции), сумма, произведение (двухместные функции), для области людей тАФ одноместные (возраст, рост), для области материальных тел тАФ объем, удельный вес.
Значения сложных термов, каковыми являются также предметы из области D, и приписывание которых составляет их интерпретацию, вычисляются в зависимости от припиВнсанных уже значений их простым составляющим тАФ предВнметным константам, предметным функторам, а также и возВнможным предметным переменным, значения которых приВнписываются по правилам II. Вычисление происходит в соотВнветствии с правилами построения сложного терма. Сложные термы образуются, как мы видели, с применением предметВнных функторов и строятся индуктивно. Значение такого терВнма вычисляется последовательно в соответствии с порядком его построения.
Пример. Имеем терм fВІтВБ(fВІтВБ(aтВБ , aтВВ), fВІтВВ(aтВБ, aтВГ)).
Пусть область D тАФ целые положительные числа, aтВБ есть число 3, aтВВ =4, aтВГ = 5, fВІтВБ тАФ сумма, fВІтВВ тАФ произведение.
Тогда
fВІтВБ(aтВБ , aтВВ)=7;
fВІтВВ(aтВБ, aтВГ)=15;
fВІтВБ(fВІтВБ(aтВБ , aтВВ), fВІтВВ(aтВБ, aтВГ))=22.
II. Свободным переменным в той или иной формуле (а тем самым и в составе термов этой формулы) в качестве значений приписывают, также как и постоянным термам, предметы из области D. Такие приписывания осуществляютВнся когда мы хотим получить из интерпретированной формуВнлы со свободными переменными высказывание нашего языВнка. Приписывание осуществляют заменой каждого вхождеВнния некоторой свободной переменной какой-либо предметВнной константой с одновременной интерпретацией таковой, если она еще не была интерпретирована в формуле.
Будем говорить, что при осуществлении этих приписываВнний в добавление к уже имеющейся интерпретации формуВнлы, формула оказывается полностью интерпретированной.
Однако важно заметить, что формулы со свободными пеВнременными нужны не только для образования высказываний из них. Они представляют собой особые высказывательные формы, называемые предикатами. Это сложные знаковые формы возможных свойств предметов заданной области и возможных отношений среди этих предметов. По типу их предметных значений они должны быть отнесены к категоВнрии предакаторов. Можно назвать их сложными предикаторами (в отличие от простых, указанных среди исходных симВнволов). Надо отметить, что эти формы не выделяются и даже не замечаются в естественных языках. Они играют, однако, решающую роль в теории понятия. Имея тот или иной предикат, можно ставить вопрос, для каких предВнметов, которые могут представлять свободные переменные, этот предикат выполняется или не выполняется. В таком слуВнчае мы просто указываем предметы для соответствующих переменных (не осуществляя указанных подстановок предВнметных констант вместо них). Например, можно сказать, что предикат Вл(Р2(x, aтВБ) > тИГyQ2(x, y))В», тАФ выражающий свойство какого-то числа х из области натуральных чисел, состоящее в том, что Влесли это число больше 5 (знаками отношения ВлбольшеВ» и Вл5В» является соответственно Р2 и aтВБ то оно деВнлится без остатка (Q2) на некоторое число уВ», выполняется для чисел 6, 8, 9 и т. д., но не выполняется для 7, 11 и др.
III. Приписывание истинностных значений полностью интерпретированным формулам.
Напомним, что полностью интерпретированная формуВнла тАФ это формула, в которой осуществлена интерпретация дескриптивных постоянных и приписано значение всем своВнбодным переменным, если таковые имеются в ней. Каждая такая формула представляет собой определенное высказываВнние тАФ с определенным смыслом и истинностным значениВнем тАФ но лишь при условии, если нам известны значения встречающихся в ней тАФ явным или неявным образом тАФ лоВнгических констант, (которые и определяются рассматриваеВнмыми правилами III). Явным образом указываются тАФ в сложных формулах тАФ логические константы, перечисленВнные в списке исходных символов. Простые атомарные форВнмулы видов PтБї (tтВБ, тАж,tn)
по-видимому, не содержат логичеВнских констант. Однако, неявным образом здесь присутствует логическое отношение принадлежности свойства Р некотоВнрому предмету t при n= 1 или о наличии отношения PтБї межВнду предметами tтВБ, тАж,tn из области D.
Определение значений всех логических терминов, как явно обозначенных, так и неявно содержащихся в формуВнлах, осуществляется как раз посредством правил приписываВнния истинностных значений полностью интерпретированВнным формулам нашего языка (строго говоря, мы имеем здесь так называемое неявное определение логических констант, но они достаточны для понимания того, какой именно смысл они придают нашим высказываниям).
Правила эти таковы. Значение простого (атомарного) выВнсказывания PтБї (tтВБ, тАж,tn), n >= 1, определяется в зависимости от заданных значений термов tтВБ, тАж,tn и предикатора PтБї . Оно заВнвисит от характера предметов данной предметной области. Положим, имеем формулу: PВІ(fВ№тВБ (aтВБ), fВ№тВБ(aтВВ)). Предположим, что согласно заданной интерпретации D тАФ множество люВндей: Р2 означает ВлбольшеВ»: fВ№тВБ ВлвозрастВ»: aтВБ тАФ Петров, aтВВ тАФ Сидоров. Вся формула представляет собой высказывание ВлВозраст Петрова больше, чем возраст СидороваВ». Высказывание истинно или ложно в зависимости от того, имеет или не имеет место данное отношение между возрастами Петрова и Сидорова.
Заметим, что в части лексики мы перевели здесь высказываВнние, полученное из определенной формулы рассматриваемого языВнка (ЯКЛП), по существу на обычный естественный русский язык. В самом ЯКЛП знаковой формой его является упомянутая формула. Подобные переводы обычно напрашиваются сами собой в силу того, что задание значений отдельных терминов тАФ составляющих формулу тАФ осуществляется посредством выражений естественноВнго языка. Мы говорим Влзначение Р2 тАФ больше, aтВБ и aтВВ тАФ соответВнственно Сидоров и ПетровВ» и т. п.). Это значит, что приписывание предметных значений выражениям описываемого языка осущеВнствляется методом перевода их в тот или иной естественный язык. Может показаться, что при упомянутых переводах высказываний данного языка на естественный теряется та самая точность их выВнражений, ради достижения которой как раз и строятся формализоВнванные языки. Однако точность здесь по сравнению с естественВнными языками достигается не за счет более точною употребления отдельных терминов, тАФ достаточная точность их уже должна быть обеспечена при осуществлении интерпретации выражений формаВнлизованного языка тАФ а за счет определенных, стандартных спосоВнбов построения высказываний и их логических форм. И она именВнно сохраняется, или точнее сказать, должна сохраняться при укаВнзанных переводах.
Для сложных формул имеем, предполагая, что все составляюВнщие их формулы полностью интерпретированы.
Формула вида А & В имеет значение ВлистинаВ» тАФ при данной интерпретации и приписывании значений свободным переменВнным тАФ е. т. е. А имеет значение И и В имеет значение И.
Формула A v В тАФ истина е. т. е. значение А равно И или значеВнние В равно И.
Формуле вида А тКГ В приписывается значение И е. т. е. А имеет значение Л или В имеет значение И.
Значением формул вида ВмА является И е.т.е. значение А есть Л.
Формула вида тИАх А(х) имеет значение ВлистинаВ» е. т. е. для всяВнкого предмета а(i) из D, А(а(i)) тАФ истина (А(а(i)) тАФ результат замеВнщения всех свободных вхождений х в А(х) константой а(i)В№).
Формула вида тИГ х А(х) имеет значение истина е. т. е. существует предмет а в области D такой, что истинна формула A(a(i)).
Если значение некоторой формулы не является И, то она имеет значение Л, но никакая формула не имеет одновременно значения И и Л.
Как уже говорилось, правила приписывания истинностных знаВнчений полностью интерпретированным формулам неявным обраВнзом определяют также значения логических констант Вл&В», ВлvВ», ВлтКГ В», ВлВмВ» и кванторов тИА и тИГ и вместе с тем и смыслы высказываВнний, образованных посредством соответствующих констант. НаВнпример, высказывания вида тИАх А(х) , тИГ х А(х) ,относящиеся к некоВнторой области индивидов D, мы должны понимать, соответственно, как Влдля всякого предмета х из D верно А(х}В» и Влсуществует предВнмет х в D такой, что верно А(х)В». Нетрудно видеть, что &, v, тКГ ,Вм , представляют собой здесь логические связки тАФ знаки функций исВнтинности, тАФ определенные ранее в разделе ВлЛогика высказываВннийВ», но теперь применительно к формулам ЯЛП.
Примеры
Определим значение формулы тАФ
тИАx((PВІ(x, aтВБ) & PВІ((x, aтВВ))тКГ PВІ(x,y))
при условии, что область возможных значений переменных D есть множество целых положительных чисел, константам aтВБ и aтВВ приписаны соответственно числа 2 и 3, свободной пеВнременной у тАФ значение 6; предикатный символ Р2 имеет в качестве значения отношения ВлделитсяВ». Ясно, что при укаВнзанной интерпретации данная формула выражает определенВнное высказывание: в переводе на русский язык, ВлДля всякоВнго целого положительного числа х верно, что если оно делитВнся на 2 и на 3, то оно делится на 6В». Ясно, что это высказыВнвание и соответственно наша формула истинны. Рассмотрим формулу тИАx тИГy PВІ(y, x). Если D тАФ множество людей, Р2 тАФ отец, то она представляет собой высказывание ВлДля всякого человека х существует человек у такой, что он является отВнцом первогоВ».
Как уже сказано, полностью интерпретированные форВнмулы языка при учете правил III представляют собой выскаВнзывания этого языка, а интерпретированные формулы со свободными переменными тАФ предикаты (знаковые формы сложных свойств и отношений соответствующей области предметов D). Неинтерпретированные формулы, не содержаВнщие свободных переменных, тАФ суть логические формы выВнсказываний, а со свободными переменными тАФ логические формы предикатов. Однако предикаты могут трактоваться и трактуются в процессах выводов и доказательств, а также в определении отношения логическою следования и законов логики как специфические высказывания с какими-то подраВнзумеваемыми значениями переменных, как это делается, наВнпример, в записи математических уравнений.
Возможность различных истолкований формул со свободными переменными указывает на существование различных истолковаВнний или, как говорят, различных интерпретаций самих свободных переменных в формулах. Вообще различают три возможных инВнтерпретации свободных переменных в составе формул ЯКЛП.
1) Предикатная интерпретация. Она означает, что свободные переВнменные в формуле рассматриваются как знаки пустых мест в предикате, на которые могут подставляться имена предметов из заВнданной области D для образования высказываний из предикатов.
2) Условная интерпретация. 3) Интерпретация всеобщности.
При второй и третьей интерпретации свободных переменных формула, содержащая эти переменные, трактуется как высказываВнние или логические формы таковых (в зависимости от того, являВнются они интерпретированными или нет). При условной интерпреВнтации некоторой переменной в нем эта переменная рассматриваетВнся как знак какого-то тАФ одного и того же во всех своих вхождениВнях тАФ предмета из области D. А при интерпретации всеобщности какой-либо переменной она рассматривается как знак любого предметы из области D, но одного и того же во всех своих вхождеВнниях в формулу. Иначе говоря, высказывание со свободными переВнменными равносильно высказыванию, которое получается из данВнного посредством связывания всех его свободных переменных, взятых в условной интерпретации, квантором существования, а пеВнременных, рассматриваемых в интерпретации всеобщности, кванВнтором общности. В предыдущем описании семантики мы подразуВнмеваем предикатную интерпретацию свободных переменных. А высказывание, получаемое из предиката, тАФ как результат примеВннения этого предиката к предметам, имена которых подставляются вместо свободных переменных. Однако в дальнейшем, например при анализе понятия следования, формулы со свободными переВнменными трактуются как высказывания с условной интерпретаВнцией этих переменных.
Подчеркнем еще раз значение интерпретации (совокупность правил I). При наличии правил III, то есть при заданном понимании логических констант, определяющих тип языка, различные интерпретации порождают из заданной синтаксической системы фактически различные языки данного типа (в которых используетВнся каждый раз лишь какая-то часть исходных дескриптивных симВнволов).
В заключение данного раздела, касающегося семантики языка, важно заметить, что хотя правила приписывания знаВнчений выражениям языка, составляющих в совокупности эту семантику, ориентированы на приписывание значений в каВнких-то конкретных случаях, их основное значение состоит в том, что они указывают общие принципы, общие способы превращения формул языка в осмысленные выражения. При таком истолковании указанных правил семантика представВнляет собой теорию означивания выражений данного языка (которую называют также теорией референВнции).
Данные выше разъяснения относительно тех смыслов, которые формулы получают при интерпретации, указывают на принципы перевода высказываний языка логики предикаВнтов на естественный язык. Однако в них можно усмотреть решение и обратной задачи тАФ перевод с естественного на язык логики предикатов, хотя здесь требуются и определенВнные дополнительные разъяснения. Прежде всего они связаВнны с отсутствием в формулах ЯЛП общих имен. Общие имеВнна здесь используются только для характеристики задаваеВнмой каждый раз при выражении некоторого высказывания области D значений предметных переменных. В составе саВнмих формул общие имена тАФ в предложениях обычного языВнка тАФ заменяются предикаторами. Так, предложение ВлВсе студенты пединститута готовятся стать преподавателямиВ» может быть переведено на язык логики предикатов двояко в зависимости от выбора значений переменных. Мы можем взять в качестве таковой Влмножество студентов пединституВнтаВ». Обозначив тогда через P1 свойство Влготовятся стать преВнподавателямиВ», получим ВлтИАx P'(x)В». С учетом заданной обВнласти это должно быть прочитано как Влвсякий студент пеВндинститута х готовится стать преподавателемВ». Для более полного выражения смысла высказывания можем взять в каВнчестве области ВлстудентыВ» вообще, а общее имя Влстудент пеВндинститутаВ» истолковать как предикатор, взяв для него, например, знак (предикатор) S1 получим тИАx (S1(x) тКГ P1(x). Предложение звучит теперь так: ВлДля всякого студента х верно, что если он учится в пединституте, то он готовится стать преподавателемВ». Высказывание ВлНекоторые студенты пединститута готовятся стать преподавателямиВ» при том же выборе области D и предикаторов запишется в виде тИГx(S(x)&P(x))
Обратите внимание, когда высказывание предваряет квантор общности (то есть исходное высказывание является общим), то далее используется логическая связка тКГ; в слуВнчае, когда таковым является квантор существования (выскаВнзывание является частным), то для его записи на ЯЛП упоВнтребляется связка &.
Для полной записи предложения ВлВо всяком государстве имеется город, который является его столицейВ» напрашиваВнется необходимость ввести предикаторы: государство с аргуВнментом тАФ х (возьмем для обозначения из исходных симвоВнлов предикатор P1), город с аргументом тАФ у (обозначим его Q), принадлежит тАФ город у государству х (обозначим R2) и столица тАФ город y государства х (обозначение S2). В таком случае возникает трудность с характеристикой области знаВнчений переменных х, у. Можно считать, что таковой являетВнся множество населенных людьми территорий. Взяв в качеВнстве области D множество таких территорий и используя указанные предикаторы, получим запись нашего суждения в ЯЛП: тИАx(P(x) тКГ (тИГy(Q(y)&R(y, x)&S(y, x))). Буквальное произВннесение его таково: ВлДля всякой населенной территории х верно, что если х есть государство, то существует населенВнная территория у, такая, что у тАФ город и у принадлежит гоВнсударству х, а у есть столица х.
Как мы видели, высказывания естественного языка, подВнлежащие переводу на ЯЛП, определенным образом стандарВнтизируются, четко выделяются части высказывания: классы или отдельные предметы, о которых нечто утверждается (или отрицается). Если это классы, то выясняется, ко всем предметам класса или лишь к части их относится утверждеВнние или отрицание (соответственно употребляются кванторы общности тИА или существования тИГ). И наконец, определяется то, что именно в высказывании утверждается (или отрицаетВнся). Примеры таких стандартизации высказываний естеВнственного языка, осуществленные еще до записи их на ЯЛП, читатель может найти в самом начале данного параграфа.
ЛОГИКА ПРЕДИКАТОВ
Логика предикатов формируется аналогично тому, как это происходит относительно логики высказываний. При наВнличии определений логических констант тАФ как логики выВнсказываний, так и логики предикатов, тАФ последняя опредеВнляется введением понятий логического следования для форВнмул ЯЛП и закона логики предикатов.
ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ
Как и в логике высказываний, мы говорим, что для выВнсказываний AтВА и BтВА (выраженных теперь в описанном языке логики предикатов), имеет место отношение логического следования AтВА тКи BтВА, если и только если оно имеет место для формул А и В1 представляющих собой логические формы указанных высказываний.
Последнее получается из AтВА и BтВА просто отвлечением от имеющихся значений их дескриптивных терминов. При этом, возможно, что AтВА или BтВА ,а также и то и другое, содерВнжат свободные переменные и трактуются при этом как выВнсказывания с неопределенными истинностными значениями, в которых подразумевается, что каждая свободная переменВнная имеет какое-то определенное значение (во всех местах, где она встречается в том или ином выводе или доказательВнстве, или вообще в некотором рассуждении).
Очевидно, что в упомянутых высказываниях со свободными переменными эти переменные имеют условную интерпретацию, которой мы будем придерживаться и в дальнейшем, хотя не исВнключаем возможность употребления таких высказываний, наприВнмер в выводах и доказательствах с интерпретацией всеобщности их свободных переменных. Строго говоря, именно условная интерВнпретация соответствует понятию логического следования. А в слуВнчае интерпретации всеобщности при построении выводов и докаВнзательств, требуются особые ограничения.
Отношение следования между формулами AтВА тКи BтВА имеет место е. т. е. при любой интерпретации дескриптивных терВнминов в А и В и при любых приписываниях значений своВнбодным переменным при истинности первого истинно и втоВнрое, иначе говоря, ложно первое или истинно второе. ИмеетВнся в виду при этом, что, во-первых, если некоторый дескрипВнтивный термин каким-то образом интерпретирован в А, то таким же образом он интерпретирован и в В (конечно, при наличии его в этой формуле), а, во-вторых, всем свободным вхождениям одной и той же переменной в А и В приписываВнется одно и то же значение. Из множества высказываний Г тВА
следует высказывание B тВА если и только если это отношение имеет место соответственВнно между множеством формул Г и В, представляющих собой логические формы упомянутых высказываний. Последнее же отношение Г тКиВ имеет место, е. т. е. в составе Г имеется конечное подмножество формул А1, .., Аn (n >= 1) такое, что (А1 & .. & Аn) тКи В. Последнее соотношение, как и в логике выВнсказываний, равносильно тому, что из множества высказыВнваний А1, .., Аn следует В, что в свою очередь указывает на отмеченное ранее тАФ в логике высказываний тАФ свойство отношения следования, состоящее в том, что если некоторое высказывание следует из какого-то множества высказываВнний, то оно является следствием также любого расширения этого множества.
ЗАКОН ЛОГИКИ ПРЕДИКАТОВ
Формула А описанного языка логики предикатов является законом данной логической системы, то есть (тКиА) е. т. е. при любой ее интерпретации и при любых приписываниях знаВнчений ее свободным предметным переменным в заданной области D. Получаемое высказывание является истинным. Законы логики предикатов называются также универсально-общезначимыми формулами логики предикатов.
тАв Формула А называется общезначимой в некоторой области D е. т. е. она истинна при любых приписываниях значений ее дескриптивным терминам и свободным переменным в этой обВнласти D. Формула А называется выполнимой, если она истинВнна при какой-нибудь интерпретации и при каком-нибудь приВнписывании значений ее свободным предметным переменным. В противном случае она называется невыполнимой.
Поскольку в язык логики предикатов, как это иногда деВнлается, мы не включаем пропозициональные переменные, никакая формула логики высказываний не является формуВнлой логики предикатов. Однако из любого закона логики выВнсказываний получается закон логики предикатов при подстаВнновке вместо пропозициональных переменных любых форВнмул логики предикатов (при замене каждого вхождения каВнкой-нибудь пропозициональной переменной одной и той же формулой логики предикатов; хотя не исключается при этом замена разных пропозициональных переменных одной и той же формулой логики предикатов).
Так же, как и в логике высказываний, здесь введением указанных понятий тАФ законов логики предикатов и логичеВнского следования тАФ в сочетании с определениями логичеВнских констант задается бесконечное множество случаев отВнношения логического следования и бесконечное множество законов логики. Однако в отличие от логики высказываний мы не имеем теперь общих процедур для решения вопросов о том, имеет ли место отношение логического следования между множеством формул Г и формулой В (или между двуВнмя формулами А и В) и является ли некоторая формула А заВнконом логики. Эта специфика логики предикатов характериВнзуется как неразрешимость этой теории относительВнно универсальной общезначимости формул. Эта ограниченВнность наших возможностей здесь является платой за отказ от принимаемых в логике высказываний абстракций относиВнтельно структур некоторых высказываний.
Как и в логике высказываний, мы имеем здесь связь между отношением следования и законаВнми логики. Она позволяет сводить вопрос о наличии или отсутствии отношения следования для конечных множеств формул к вопросу о том, является ли некоторая формула универсально общезначимой. Имеется в виду связь
А1, .. Аn тКи В е. т. е. тКи (А1 тКГ (А2тКГ (А2 тКГ .. (АnтКГ В) ..));
последняя же, как мы видели раньше, равносильна тКи ((А1 &А2 & .. &An) тКГ В) тАФ при любой расстановке скобок в конъюнкции согласно правилам построения формул.
В связи с отмеченной неразрешимостью логики предикаВнтов особое значение приобретает здесь формализация поняВнтий следования и закона логики посредством построения лоВнгических исчислений. Именно исчисление дает возможность во многих случаях синтаксическим образом решать вопрос, является ли некоторая формула законом, или соответственно есть ли некоторое отношение следования, когда мы не моВнжем решить этот вопрос посредством семантического аналиВнза. Для логики высказываний исчисление высказываний, воВнобще говоря, не является необходимым. Оно скорее нужно как часть логического исчисления для формул ЯЛП.
ИiИСЛЕНИЕ ПРЕДИКАТОВ
В основе исчисления предикатов лежит язык логики преВндикатов. В остальном оно является расширением исчисления высказываний.
Аксиоматическую систему исчисления предикатов мы поВнлучим, добавив к перечисленным выше схемам аксиоматиВнческого исчисления высказываний (имея в виду, конечно, переход к языку логики предикатов) следующие четыре схеВнмы и одно правило:
1. тИАx A(x) тКГ A(t) тАФ схема тИАи .
2. A(t) тКГтИГх А(х) тАФ схема тИГв.
3. тИАx (В тКГ С(х)) тКГ (В тКГтИАx С(х)) схема введения тИА в консеквент .
4. тИАx (С(х) тКГ В) тКГ (тИГxтКГC(x) тКГ В) тАФ схема введения тИГ в антеВнцедент.
A(t) тАФ результат правильной подстановки терма ( вместо х в А(х); В тАФ не содержит х свободно.
Правило тИАв (правило введения квантора общности, иное
A(t) название: правило обобщения): тАФтАФ (из А непосредственно
выводимотИАx A).
Формально мы сохраняем прежнее определение вывода и доказательства (ясно, что, по существу, изменение состоит в том, что теперь могут использоваться новые аксиомы и ноВнвое правило), однако, если мы хотим, чтобы отношение форВнмальной выводимости было аналогом семантического поняВнтия следования, необходимо ограничить применение тИАв : оно может применяться к некоторой формуле А(х) для обобщеВнния лишь по таким переменным х, которые не содержатся свободно в допущениях, от которых зависит эта формула. Чтобы смысл этого ограничения был ясным, мы должны определить понятие зависимости некоторой формулы вывоВнда от допущений (гипотез). Везде в дальнейшем будем иметь в виду выводы с анализом (то есть обоснованием каждого его шага ссылками либо на принадлежность формулы этого шага к множеству взятых гипотез или аксиом системы, либо на формулы, из которых она получатся, и используемые при этом правила).
Формула В данного вывода зависит от некоторого допуВнщения А, если и только если: а) она есть само допущение А;
б) получается из некоторых формул по правилам системы (из СтКГВ и С по m. р. или из С по тИАв), какая-нибудь из котоВнрых зависит от А. Более простым образом понятие зависимоВнсти разъясняется в описываемой далее системе натурального вывода, значительно проще осуществляются там сами вывоВнды и доказательства.
НАТУРАЛЬНАЯ СИСТЕМА ИiИСЛЕНИЯ ПРЕДИКАТОВ
Постулатами системы (исходными правилами) являются все правила натуральной системы исчисления высказываний и правила для кванторов.
Правила вывода для выражений с кванторами:
тИАв :
тИАи :
тИГв :
тИГи :
Понятие вывода и доказательства остаются формально теми же, которые были сформулированы в исчислении выВнсказываний, разница лишь в том, что при ссылке на правила вывода теперь имеются в виду и вновь введенные правила для выражений с кванторами. К числу указанных в предыдуВнщем параграфе эвристических принципов введения допущеВнний может быть добавлен еще один.
Если в выводе получена формула тИГх А(х} и нужно вывесВнти В, не выводимую непосредственно из имеющихся форВнмул, вводим допущение А(х), применяя способ рассуждения согласно тИГи.
Рассмотрим несколько примеров выводов.
Схема доказательства формул вида: ВмтИГx A(x) тКГтИАxВмA(x):
+ 1. ВмтИГx A(x) [1].
+ 2. A(x) [2].
3. тИГx A(x) [2] тАУ из 2, тИГв.
4. Вм A(x) [1] тАУ из 1,3, Вмв.
5. тИАxВмA(x) [1] тАУ из 4, тИАв.
6. ВмтИГx A(x) тКГтИАxВмA(x) [ - ] тАУ из 5, тКГв.
Схемы доказательств рассмотренных в аксиоматической системе аксиом Влвведения тИА в консеквентВ» и Влвведения тИГ в антецедентВ»:
Предполагается, что А не содержит х свободно.
+ 1. тИАx (A тКГ B(x)) [1].
+ 2. А [2].
3. A тКГ В(х) [1] тАФиз 1, тИАи.
4. В(х) [1, 2] тАФиз3 и 2, тКГи.
5. тИАx B(x) [1, 2] тАФиз 4, тИАв.
6. AтКГтИАx B(x) [1] тАФиз5, тКГв.
7. тИАx (A тКГ B(x)) тКГ (A тКГтИАx B(x)) [ - ] тАФиз 6, тКГв.
+ 1. A тКГ (В(х) тКГ A) [1].
+ 2. тИГx B(x) [2].
+ 3. В(х) [З].
4. В(х) тКГ A [1]тАФиз 1, тИАи.
5. А [1, 3] тАФ из 3, 4, тКГв.
6. A [1, 2]тАФ из 5, тИГи.
7. тИГx B(x) тКГ А [1]тАФиз 6, тКГв.
8. тИГx (B(x) тКГ А) тКГ (тИГx B(x) тКГ А) тАФ из 7, тКГв.
Сформулированное здесь исчисление, как и приведенная выше аксиоматическая система исчисления предикатов, представляет собой адекватную формализацию понятий лоВнгического следования и закона логики. Это значит, что для них справедливы теоремы:
Г тКи B е. т. е. Г тКв B и тКи A е. т. е. тКв A.
В заключение параграфа в дополнение к ранее сформуВнлированным эквивалентностям языка логики высказываний приведем схемы наиболее важных законов логики, относяВнщихся к языку логики предикатов, которые читатель может использовать также в качестве упражнений для выводов и доказательств:
I. Взаимовыразимость кванторов:
1. тИАx A(x) ~ ВмтИГxВмA(x). 2. тИГx A(x) ~ ВмтИАxВмA(x).
II. Законы образования контрадикторной противоположВнности:
1. ВмтИАx A(x) ~ тИГxВмA(x). 2. ВмтИГx A(x) ~ тИАxВмA(x).
III. Законы пронесения кванторов:
1. ((тИАx A(x) & тИАx B(x)) ~ тИАx(A(x) & B(x))).
2. ((тИГx A(x) v тИГx B(x)) ~ тИГx (A(x) v B(x))).
3. (тИГx (A(x) & B(x)) тКГ (тИГx A(x) & тИГx B(x))).
4. ((тИАx A(x) v тИАx B(x)) тКГ тИАx (A(x) v B(x))).
5. (тИАx (A v B(x)) ~ (A v тИАx B(x))), если x не свободна в A.
6. (тИГx (A & B(x)) ~ (A & тИГx B(x))), если х не свободна в А.
7. (тИАx A(x) тКГ B(x)) тКГ (тИАx A(x) тКГ тИАx B(x))).
IV. Перестановка кванторов
1. тИАx тИАy A(x, y) ~ тИАyтИАx A(x, y).
2. тИГx тИГy A(x, y) ~ тИГy тИГx A(x, y).
3. тИГx тИАy A(x, y) тКГ тИАy тИГx A(x, y).
V. Исключение квантора общности и введение квантора существования.
1. тИАx A(x) тКГ A(t). 2. A(t) тКГ тИГx A(x).
В обоих случаях А(t) есть результат правильной подстаВнновки терма t вместо х в А(х).
VI. Законы устранения вырожденных кванторов. 1. тИАx А ~ А. 2. тИГx А ~ А, где А не содержит х свободно.
VII. Связь кванторов тИА и тИГ.
тИАx A(x) тКГ тИГx A(x).
Ясно, что приведенные эквивалентности также могут быть использованы в рассуждениях посредством эквивалентВнных преобразований.
Пример эквивалентных преобразований формулы
тИАx (P(x) тКГ Вм Q(x)) тКГ Вм тИГx (P(x) & Q(x)).
с использованием некоторых из указанных в этом и предВныдущем параграфе схем эквивалентностей:
тИАx (P(x) тКГ Вм Q(x)) тКГ Вм тИГx (P(x) & Q(x)) тЙб
тЙб ВмтИАx (P(x) тКГ Вм Q(x)) v Вм тИГx (P(x) & Q(x)) тЙб
тЙб тИГx Вм(P(x) тКГ Вм Q(x)) v Вм тИГx (P(x) & Q(x)) тЙб
тЙб тИГx (P(x) & ВмВм Q(x)) v Вм тИГx (P(x) & Q(x)) тЙб
тЙб тИГx (P(x) & Q(x)) v Вм тИГx (P(x) & Q(x)) тЙб
тЙб тИГx (P(x) & Q(x)) v тИАxВм (P(x) & Q(x)) тЙб
тЙб тИГx (P(x) & Q(x)) v тИАx (ВмP(x) & ВмQ(x)).
Разработанный в современной символической логике меВнтод построения логических исчислений является важнейшим ее результатом. Его теоретическая и практическая значиВнмость состоит в том, что благодаря ему возникает возможВнность доказательства любой формулы, представляющей заВнкон логики, из бесконечного множества таких формул, а также осуществлять соответствующий вывод для любого слуВнчая тАФ опять-таки из бесконечного множества случаев от
ношения логического следования. В основе логических исВнчислений, как мы видели, лежат специальные логические языки. Наряду с рассмотренными выше возможностями исВнпользования этих языков для решения многих логических вопросов, и в первую очередь для точного определения осВнновных понятий логики (логическое следование и закон лоВнгики), следует заметить, что в этих языках имеются, по суВнществу, точные понятия логической формы и логического содержания мыслей, которые мы используем в дальнейшем.
Министерство образования Российской Федерации
Марийский Государственный Технический Университет
Факультет Информатики и Вычислительной Техники
Кафедра ИВС
Реферат
по математической логике и теории алгоритмов на тему:
тАЬСтруктура исчисления предикатов
построение логического выводатАЭ
Выполнили студенты I-го курса
Факультета ИВТ: Зубарев А., Столяров А.,
Докукин А., Китирисов Г.
Йошкар-Ола, 2003г.
Содержание:
ВведениетАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.1
Синтаксис языка логики предикатов тАжтАжтАжтАжтАжтАжтАж.1
Свободные и связные вхождения
переменных в формулытАжтАжтАжтАжтАжтАжтАжтАж3
Семантика языка логики предикатовтАжтАжтАжтАжтАжтАжтАж.4
Логика предикатовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..11
Логическое следованиетАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж11
Закон логики предикатовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.12
Исчисление предикатовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..13
Натуральная система исчисления предикатовтАжтАжтАж..15
ЛитературатАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.16
Список литературы
1. Е. К. Войшвилло, М. Г. Дегтярев Логика, Москва, 2001.
2. А.А. Марков, Н. М. Нагорный Теория алгорифмов, Москва, 1984.
Вместе с этим смотрят:
Структура сходящихся последовательностейСфераТезис Геделя. Теорема ЧерчаТела вращения