Диалектика развития понятия функции
Доклад для конференции по математике на тему:
ВлДиалектика развития понятия функцииВ»
Понятие
функци
и является одним и
з о
сновных поня
ти
и ма
Внтематики вообщ
е и школ
ьной математики в частно
сти. Оно не во
зникло
сразу в таком виде, как мы им пользуем
ся
сейчас, а как и другие
фундаментальные понятия прошло длинный пу
ть диаВнлектического и
исторического развития. Идея функциональной
зависимости восходит к древнегре
Внче
ской математике. Например, изменен
ие площ
ади, объема фигу
Внры в зависимо
сти от и
зм
енения ее размеров Однако, древними греками идея функ
циональной зави
симо
сти о
сознавала
сь
интуи
Внтивно.
Уже в 16 - 17 в. в
, техника, промышленно
сть, мореход
ство по
ставили перед математикой задачи, которые нельзя
было решить имеющимися методами математики постоянных величин. Нужны были новые математические методы, отличные от методов элементарной математики.
Впервые термин "функция" вводит в рассмотрение знаменитый немецкий математик и философ Лейбниц в 1694 г. Однако, этот термин /определения он не дал вообще/ он употребляет в узком смысле, понимая под функцией изменение ординаты кривой в зависимости от изменения ее абсциссы. Таким образом, понятие функции носит у него "геометрический налет".
Ученик Лейбница Иоганн Бернулли пошел дальше своего учителя. Он дает более общее определение функции, освобождая последнее от геометрических представлений и терминов: "функцией переменной величины называется количество, образованное каким угодно способом из этой величины и постоянных".
Под "каким угодно способом" во времена Бернулли понимали арифметические операции, извлечение корня, тригонометрические и обратные им функции; показательные, логарифмированные "операции", а также их различные комбинации.
Из сказанного выше видно, что с современной точки зрения под функцией Бернулли понимал один из способов ее задания и отождествлял понятие функции со способом задания. То есть такое определение тоже было значительно узким. Так под него не попадали такие зависимости, как
Иначе говоря, по определению Бернулли, функцией не считались функциональные зависимости /с современной точки зрения/, заданные на разных участках области определения различными аналитическими выражениями.
Однако, определение функции, данное Бернулли, устроило математиков, т.к. оно охватывало в то время все функции, какие были в употреблении и изучались математиками. Следует заметить, что подход к определению функции как к аналитическому выражению, которым оно задано, долго господствовал в математике вплоть до 18 в. Это определение полностью признавал и великий Эйлер.
Вместе с тем в математике все больше и больше накапВнливались примеры таких функций, какие не подходили под соответствующее определение. Отказать в существовании таким величинам было нельзя, т.к. они выражали определенные жизненные закономерности, но и признать их функциями было тоже нельзя, т.к. они не подходили под существующее определение. Все крупнейшие математики, в том числе и Эйлер, видели это и понимали, что нужно отказаться от существующего определения и расширить понятие функции, В этом направлении начали принимать робкие попытки Эйлер, Бернулли и др.
Вопрос о расширении понятия функции особенно остро встал в связи с решением знаменитой задачи о колебании струны. Суть этой задачи состоит в следующем: упругая струна закреплена в 2-х точках оси Ох. Затем ее оттягивают /придавая ей определенную форму/ и отпускают без начальной скорости. Струна начинает колебаться. Требуется определить ее форму в последующий момент времени.
В решении этой задачи приняли участие все крупнейшие математики того времени Эйлер, братья Бернулли, Даламбер, Лагранж, позже молодой Фурье и др. Возник спор - можно ли считать функцией решение уравнения колебания струны. Одни утверждали, что нельзя, т, к. это решение не подходило под существующее определение функции, другие считали - можно, но для этого надо расшиВнрить понятие функции. Спор длился около 40 лет и особенно острым оказался между Эйлером и Даламбером.
Предлагались различные способы записи искомой функции: в виде двух функций, задающих положение струны каждая на своем участке, или в виде 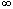 -ного ряда: U(x) = a1sin
-ного ряда: U(x) = a1sin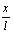 +a2sin
+a2sin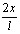 +..+ansin
+..+ansin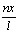 +..
+..
Но и Эйлер и Даламбер отвергли эти предложения, так как ни одна из предложенных функций не попадала под существовавшее тогда определение функции.

Итак, до возникновения спора о колебании струны все математики, современники Эйлера, в том числе и сам Эйлер, были далеки от современного понятия функции. Они связывали с понятием функции определенную формулу или аналитическое выражение, каким она задана.
При этом совершенно не представляли себе даже того, что одна и та же функция может изображаться и несколькими формулами, в зависимости от того, на каком промежутке изменения аргумента мы ее рассматриваем /кусочное задание/. Такое представление о функции и породило спор в вопросах колебания струны, длившейся в математике более 40 лет.
Окончательный разрыв между пониманиями функции и ее аналитического выражения произошел в начале 19 в., после того как французский математик Фурье показал, что функции заданные на разных участках области определения по-разному можно вообще говоря представить во всей области задания в виде суммы одного и того же  тАСного ряда. Таким образом, несущественно одним или многими выражениями задана функция суть лишь в том, какие значения принимает одна величина при заданных значениях другой величины. Открытие Фурье нанесло сокрушительный удар по догмам 18 в.
тАСного ряда. Таким образом, несущественно одним или многими выражениями задана функция суть лишь в том, какие значения принимает одна величина при заданных значениях другой величины. Открытие Фурье нанесло сокрушительный удар по догмам 18 в.
Сейчас мы знаем четыре способа задания функций: аналитический, графический, табличный и словесный, причем точно различаем само понятие функции и способы ее задания. У нас с вами функция f(x) = 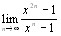 не вызывает никаких нареканий, а у математиков XVII-XVIII вв. велись острейшие споры можно ли функцию записанную не конечной формулой, а бесконечным рядом считать функцией или нет. На протяжении двух веков этот вопрос оставался открытым, а данная функция функцией не считалась. После открытия Фурье ситуация резко поменялась.
не вызывает никаких нареканий, а у математиков XVII-XVIII вв. велись острейшие споры можно ли функцию записанную не конечной формулой, а бесконечным рядом считать функцией или нет. На протяжении двух веков этот вопрос оставался открытым, а данная функция функцией не считалась. После открытия Фурье ситуация резко поменялась.
В результате Эйлер и другие крупнейшие математики пришли к выводу, что существующее понятие функции /класс аналитически изображаемых функций/ существенно уже класса всех функций вообще. Поэтому необходимо расширить это понятие.
Более широкое и уже приближающееся к современному понятие функции было дано в 1834 г. Лобачевским, он указывал на необходимость задания правила /условия/, позволяющего испытывать каждое значение х. Наконец, в 1837 г. Дирихле дал наиболее общее /классическое/ определение функции, охватывающее все содержание математики:
у есть функция от х, если всякому значению х соответствует вполне определенное значение у, причем совершенно неважно, каким именно способом установлено указанное соответствие.
В современных терминах это определение связано с понятием множества и звучит так: ВлФункция есть произвольный способ отображения множества А = {а} во множество В = {в}, по которому каждому элементу а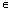 А поставлен в соответствие определенный элемент в
А поставлен в соответствие определенный элемент в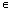 В. Уже в этом определении не накладывается никаких ограничений на закон соответствия /этот закон может быть задан Формулой, таблицей, графиком, словесным описанием/. Главное в этом определении:
В. Уже в этом определении не накладывается никаких ограничений на закон соответствия /этот закон может быть задан Формулой, таблицей, графиком, словесным описанием/. Главное в этом определении:  а
а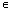 А
А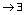 !b
!b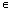 B. Под элементами множеств А и В понимаются при этом элементы произвольной природы.
B. Под элементами множеств А и В понимаются при этом элементы произвольной природы.
Это определение вполне устраивало всех математиков: под него попадали все функциональные зависимости в то время известные в математике. Оно столь широко, что им действительно охватывается все содержание и современной математики. Более того, с точки зрения общего учения о функциях та или иная отдельная математическая дисциплина характеризуется типом расс
матр
иваемых в ней функц
ий.
Так, в анализе рассматриваются функции, отображающие одно числовое множество на другое числовое множество. Если это некоторые множества действительных чисел, то имеем функцию действительной /вещественной/ переменной. Если же это некоторые множества комплексных чисел, то имеем комплексную функцию комплексной переменной.
В вариационном исчислении
основным понятием является функционал. Функционал - это соответствие, которое каждой функции из некоторого класса /который называется областью определения функции/ сопоставляет определенное число, иначе функционал отображает множество функций во множество чисел. Например,
L =  , где у = у(х) - спрямляемая плоская кривая J =
, где у = у(х) - спрямляемая плоская кривая J = 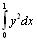
В операционном исчислении основным объектом изучения является оператор. Оператор некоторой функции ставит в соответствие другую функцию /причем функции здесь являются элементами множеств/. Например, оператор дифференцирования переводит всякую дифференцируемую функцию f одного вещественного переменного в производную f .
.
В теории чисел рассматриваются так называемые арифметические функции, т.е. функции, принимающие лишь целочисленные значения. Такие функции могут быть заданы или на множестве N /например, 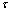 (n) и S(n) - выражающие число и сумму делителей числа n/, или на множестве R /например, {х} и [x] - дробная часть числа и наибольшее целое число, не превосходящее действительное число Х.
(n) и S(n) - выражающие число и сумму делителей числа n/, или на множестве R /например, {х} и [x] - дробная часть числа и наибольшее целое число, не превосходящее действительное число Х.
Преобразования, составляющие содержание геометрии, можно также рассматривать с точки зрения общего понятия функции. Здесь таким образом изучаются точечные соответствия, т.е. функции, отображающие геометрические образы. В связи с характером этих отображений классифицируется содержание геометрия. В элементарной геометрии изучаются движение и подобие, далее идут аффинная и проективная геометрия, конформная геометрия /характеризуемая сохранением углов при рассматриваемых в ней отображениях/, наконец, топология /изучающая в общем виде непрерывные отображения/ и т.д.
Итак, резюмируя сказанное выше, отметим, что понятие функции, оформившееся под влиянием спора о колебании струны, данное окончательно Дирихле, охватывает все содержание современной математики. Однако, развитие этого понятия не прекратилось и в настоящее время. Оно происходит внутри этого понятия в различных направлениях.
Вместе с этим смотрят:
Дидактические игры на занятиях по математикеДисперсионный анализДифференциальные уравнения I и II порядкаДоказательства теорем