Дисперсионный анализ
Министерство образования Российской Федерации
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВлОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТВ»
Факультет информационных технологий
Кафедра прикладной информатики
КУРСОВАЯ РАБОТА
По дисциплине: ВлСистемный анализВ»
На тему: ВлДисперсионный анализВ»
ГОУ ОГУ 071900.5303.09 ПЗ
Руководитель работы
|
_____________Юдина Н.М.
|
Вл___В»_____________2003 г.
|
Исполнитель
|
студент гр. 99 ИСЭ-2
|
_____________Жбанов В.В.
|
Вл___В»_____________2003 г.
|
г. Оренбург-2003
Содержание
с.
ВведениетАжтАжтАжтАжтАжтАжтАжтАж.тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..3
- Дисперсионный анализтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..4
1.1 Основные понятия дисперсионного анализатАжтАжтАжтАжтАжтАжтАж.тАжтАж4
1.2 Однофакторный дисперсионный анализтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж...6
1.3 Многофакторный дисперсионный анализтАжтАжтАжтАжтАжтАжтАжтАж.....12
- Применение дисперсионного анализа в различных задачах и
исследованияхтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..16
2.1 Использование дисперсионного анализа при изучении
миграционных процессовтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАжтАж.тАж.16
2.2 Принципы математико-статистического анализа данных
медико-биологических исследованийтАжтАжтАжтАжтАж..тАжтАжтАжтАжтАжтАж.тАжтАжтАжтАжтАж17
2.3 Биотестирование почвытАжтАжтАжтАжтАж..тАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж..19
2.4 Грипп вызывает повышенную выработку гистаминатАжтАжтАжтАж.тАж.21
2.5 Дисперсионный анализ в химиитАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..тАж.тАж.22
2.6 Использование прямого преднамеренного внушения в
бодрствующем состоянии в методике воспитания физических качествтАжтАжтАж23
2.7 Купирование острой психотической симптоматики у больных
шизофренией атипичным нейролептикомтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.26
2.8 Снование фасонной пряжи с ровничным эффектомтАжтАжтАжтАж...тАж.28
2.9 Сопутствующая паталогия при полной утрате зубов у лиц
пожилого и старческого возрастатАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..тАжтАжтАжтАжтАжтАж29
3 Дисперсионный анализ в контексте статистических
методовтАж..........................................................31
3.1 Векторные авторегрессиитАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..тАжтАж.34
3.2 Факторный анализтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж37
3.3 Парная регрессия. Вероятностная природа регрессионных
моделейтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж.тАж41
ЗаключениетАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.тАж... 44
Список использованных источниковтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж..тАж.45
Введение
Цель работы: познакомится с таким статистическим методом, как дисперсионный анализ.
Дисперсионный анализ (от латинского Dispersio тАУ рассеивание) тАУ статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике, медицине и др.
Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации /1/.
При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии.
При проведении исследования рынка часто встает вопрос о сопоставимости результатов. Например, проводя опросы по поводу потребления какого-либо товара в различных регионах страны, необходимо сделать выводы, на сколько данные опроса отличаются или не отличаются друг от друга. Сопоставлять отдельные показатели не имеет смысла и поэтому процедура сравнения и последующей оценки производится по некоторым усредненным значениям и отклонениям от этой усредненной оценки. Изучается вариация признака. За меру вариации может быть принята дисперсия. Дисперсия ПГ2 тАУ мера вариации, определяемая как средняя из отклонений признака, возведенных в квадрат.
На практике часто возникают задачи более общего характера тАУ задачи проверки существенности различий средних выборочных нескольких совокупностей. Например, требуется оценить влияние различного сырья на качество производимой продукции, решить задачу о влиянии количества удобрений на урожайность с/х продукции.
Иногда дисперсионный анализ применяется, чтобы установить однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предполоВнжению; если дисперсионный анализ покажет, что и математические ожидания одинаковы, то в этом смысле совоВнкупности однородны). Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы /2/.
1 Дисперсионный анализ
1.1 Основные понятия дисперсионного анализа
В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель дисперсионного анализа с фиксированными уровнями факторов называют моделью I, модель со случайными факторами - моделью II. Благодаря варьированию фактора можно исследовать его влияние на величину отклика. В настоящее время общая теория дисперсионного анализа разработана для моделей I.
В зависимости от количества факторов, определяющих вариацию результативного признака, дисперсионный анализ подразделяют на однофакторный и многофакторный.
Основными схемами организации исходных данных с двумя и более факторами являются:
- перекрестная классификация, характерная для моделей I, в которых каждый уровень одного фактора сочетается при планировании эксперимента с каждой градацией другого фактора;
- иерархическая (гнездовая) классификация, характерная для модели II, в которой каждому случайному, наудачу выбранному значению одного фактора соответствует свое подмножество значений второго фактора.
Если одновременно исследуется зависимость отклика от качественных и количественных факторов, т.е. факторов смешанной природы, то используется ковариационный анализ /3/.
При обработке данных эксперимента наиболее разработанными и поэтому распространенными считаются две модели. Их различие обусловлено специфиВнкой планирования самого эксперимента. В модели дисперсионного анализа с фикВнсированными эффектами исследователь намеренно устанавлиВнвает строго определенные уровни изучаемого фактора. ТерВнмин Влфиксированный эффектВ» в данном контексте имеет тот смысл, что самим исследователем фиксируется количеВнство уровней фактора и различия между ними. При повтореВннии эксперимента он или другой исследователь выберет те же самые уровни фактора. В модели со случайными эффекВнтами уровни значения фактора выбираются исследователем случайно из широкого диапазона значений фактора, и при повторных экспериментах, естественно, этот диапазон буВндет другим.
Таким образом, данные модели отличаются между собой способом выбора уровней фактора, что, очевидно, в перВнвую очередь влияет на возможность обобщения полученных экспериментальных результатов. Для дисперсионного анализа однофакторных экВнспериментов различие этих двух моделей не столь существенВнно, однако в многофакторном дисперсионном анализе оно может оказаться весьма важным.
При проведении дисперсионного анализа должны выполняться следующие статистические допущения: независимо от уровня фактора величины отклика имеют нормальный (Гауссовский) закон распределения и одинаковую дисперсию. Такое равенство дисперсий называется гомогенностью. Таким образом, изменение способа обработки сказывается лишь на положении случайной величины отклика, которое характеризуется средним значением или медианой. Поэтому все наблюдения отклика принадлежат сдвиговому семейству нормальных распределений.
Говорят, что техника дисперсионного анализа является "робастной". Этот термин, используемый статистиками, означает, что данные допущения могут быть в некоторой степени нарушены, но несмотря на это, технику можно использовать.
При неизвестном законе распределения величин отклика используют непараметрические (чаще всего ранговые) методы анализа.
В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия ПГ2. Она является мерой вариации частных средних по группам 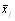 вокруг общей средней
вокруг общей средней 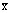 и определяется по формуле:
и определяется по формуле:
 ,
,
где k - число групп;
nj - число единиц в j-ой группе;
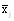 - частная средняя по j-ой группе;
- частная средняя по j-ой группе;
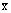 - общая средняя по совокупности единиц.
- общая средняя по совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия ПГj2.
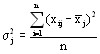 .
.
Между общей дисперсией ПГ02, внутригрупповой дисперсией ПГ2 и межгрупповой дисперсией 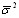 существует соотношение:
существует соотношение:
ПГ02 = 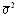 + ПГ2.
+ ПГ2.
Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе /2/.
1.2 Однофакторный дисперсионный анализ
Однофакторная дисперсионная модель имеет вид:
xij = Ој + Fj + Оµij, (1)
где хij тАУ значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,..,т) c j-м порядковым номером (j=1,2,..,n);
Fi тАУ эффект, обусловленный влиянием i-го уровня фактора;
Оµij тАУ случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня.
Основные предпосылки дисперсионного анализа:
- математическое ожидание возмущения Оµij равно нулю для любых i, т.е.
M(Оµij) = 0; (2)
- возмущения Оµij взаимно независимы;
- дисперсия переменной xij (или возмущения Оµij) постоянна длялюбых i, j, т.е.
D(Оµij) = ПГ2; (3)
- переменная xij (или возмущение Оµij) имеет нормальный законраспределения N(0;ПГ2).
Влияние уровней фактора может быть как фиксированным или систематическим (модель I), так и случайным (модель II).
Пусть, например, необходимо выяснить, имеются ли сущестВнвенные различия между партиями изделий по некоторому показаВнтелю качества, т.е. проверить влияние на качество одного фактора - партии изделий. Если включить в исследование все партии сырья, то влияние уровня такого фактора систематическое (модель I), а полученные выводы применимы только к тем отдельным партиВням, которые привлекались при исследовании. Если же включить только отобранную случайно часть партий, то влияние фактора случайное (модель II). В многофакторных комплексах возможна смешанная модель III, в которой одни факторы имеют случайные уровни, а другие тАУ фиксированные.
Пусть имеется m партий изделий. Из каждой партии отобрано соответственно n1, n2, тАж, nm изделий (для простоты полагается, что n1=n2=..=nm=n). Значения показателя качества этих изделий представлены в матрице наблюдений:
x11 x12 тАж x1n
x21 x22 тАж x2n
тАжтАжтАжтАжтАжтАжтАж = (xij), (i = 1,2, тАж, m; j = 1,2, тАж, n).
xm1 xm2 тАж xmn
Необходимо проверить существенность влияния партий изВнделий на их качество.
Если полагать, что элементы строк матрицы наблюдений тАУ это численные значения случайных величин Х1,Х2,..,Хm, выражающих качество изделий и имеющих норВнмальный закон распределения с математическими ожиданиями соответственно a1,а2,..,аm и одинаковыми дисперсиями ПГ2, то данная задача сводится к проверке нулевой гипотезы Н0: a1=a2 =..= аm, осуществляемой в дисперсионном анализе.
Усреднение по какому-либо индексу обозначено звездочкой (или точкой) вместо индекса, тогда средний показатель качества изделий i-й партии, или групповая средняя для i-го уровня фактоВнра, примет вид:
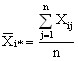 , (4)
, (4)
где 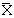 i* тАУ среднее значение по столбцам;
i* тАУ среднее значение по столбцам;
 ij тАУ элемент матрицы наблюдений;
ij тАУ элемент матрицы наблюдений;
n тАУ объем выборки.
А общая средняя:
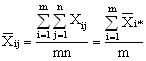 . (5)
. (5)
Сумма квадратов отклонений наблюдений хij от общей средней 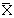 ** выглядит так:
** выглядит так:
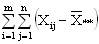 2=
2=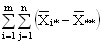 2+
2+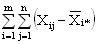 2+
2+
+2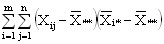 2. (6)
2. (6)
или
Q = Q1 + Q2 + Q3.
Последнее слагаемое равно нулю
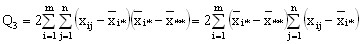 =0. (7)
=0. (7)
так как сумма отклонений значений переменной от ее средней равна нулю, т.е.
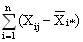 2=0.
2=0.
Первое слагаемое можно записать в виде:

В результате получается тождество:
Q = Q1 + Q2, (8)
где 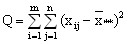 - общая, или полная, сумма квадратов отклонений;
- общая, или полная, сумма квадратов отклонений;
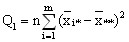 - сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
- сумма квадратов отклонений групповых средних от общей средней, или межгрупповая (факторная) сумма квадратов отклонений;
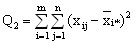 - сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
- сумма квадратов отклонений наблюдений от групповых средних, или внутригрупповая (остаточная) сумма квадратов отклонений.
В разложении (8) заключена основная идея дисперсионного анализа. Применительно к рассматВнриваемой задаче равенство (8) показывает, что общая вариаВнция показателя качества, измеренная суммой Q, складывается из двух компонент тАУ Q1 и Q2, характеризующих изменчивость этого показателя между партиями (Q1) и изменчивость внутри партий (Q2), характеризующих одинаковую для всех партий вариацию под воздействием неучтенных факторов.
В дисперсионном анализе анализируются не сами суммы квадратов отклонений, а так называемые средние квадВнраты, являющиеся несмещенными оценками соответствуюВнщих дисперсий, которые получаются делением сумм квадратов отклонений на соответствующее число степеней свободы.
Число степеней свободы определяется как общее число наблюдений минус число связывающих их уравнеВнний. Поэтому для среднего квадрата s12, являющегося несмеВнщенной оценкой межгрупповой дисперсии, число степеней свободы k1=m-1, так как при его расчете используются m групповых средних, связанных между собой одним уравнением (5). А для среднего квадрата s22, являющегося несмещенной оценкой внутригрупповой дисперсии, число степеней свободы k2=mn-m, т.к. при ее расчете используются все mn наблюдений, связанных между собой m уравнениями (4).
Таким образом:
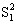 = Q1/(m-1),
= Q1/(m-1),
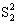 = Q2/(mn-m).
= Q2/(mn-m).
Если найти математические ожидания средних квадратов 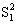 и
и 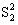 , подставить в их формулы выражение xij (1) через параметВнры модели, то получится:
, подставить в их формулы выражение xij (1) через параметВнры модели, то получится:
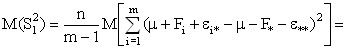

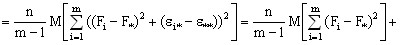
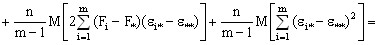
 (9)
(9)
т.к. с учетом свойств математического ожидания
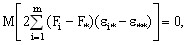 а
а
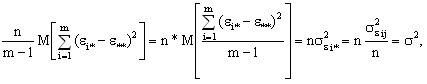
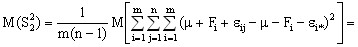
 (10)
(10)
Для модели I с фиксированными уровнями факВнтора Fi(i=1,2,..,m) тАУ величины неслучайные, поэтому
M(S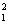 ) =
) =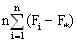 2 /(m-1) +ПГ2.
2 /(m-1) +ПГ2.
Гипотеза H0 примет вид Fi = F*(i = 1,2,..,m), т.е. влияние всех уровней фактора одно и то же. В случае справедливости этой гипотезы
M(S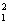 )= M(S
)= M(S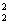 )= ПГ2.
)= ПГ2.
Для случайной модели II слагаемое Fi в выражении (1) тАУ величина случайная. Обозначая ее дисперсией
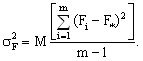
получим из (9)
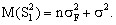 (11)
(11)
и, как и в модели I
M(S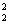 )= ПГ2.
)= ПГ2.
В таблице 1.1 представлен общий вид вычисления значений, с помощью дисперсионного анализа.
Таблица 1.1 тАУ Базовая таблица дисперсионного анализа
Компоненты дисперсии
|
Сумма квадратов
|
Число степеней свободы
|
Средний квадрат
|
Математическое ожидание среднего квадрата
|
Межгрупповая
|

|
m-1
|
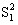 = Q1/(m-1) = Q1/(m-1)
|
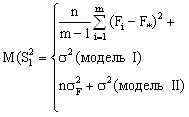
|
Внутригрупповая
|
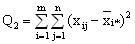
|
mn-m
|
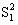 = Q2/(mn-m) = Q2/(mn-m)
|
M(S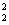 )= ПГ2 )= ПГ2
|
Общая
|

|
mn-1
|
|
|
Гипотеза H0 примет вид ПГF2 =0. В случае справедливости этой гипотезы
M(S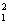 )= M(S
)= M(S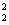 )= ПГ2.
)= ПГ2.
В случае однофакторного комплекса как для модели I, так и модели II средние квадраты S2 и S2, являются несмещенными и независимыми оценками одной и той же дисперсии ПГ2.
Следовательно, проверка нулевой гипотезы H0 свелась к проверке существенности различия несмещенных выборочных оценок S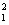 и S
и S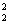 дисперсии ПГ2.
дисперсии ПГ2.
Гипотеза H0 отвергается, если фактически вычисленное знаВнчение статистики F = S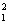 /S
/S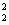 больше критического FО±:K1:K2, опредеВнленного на уровне значимости О± при числе степеней свободы k1=m-1 и k2=mn-m, и принимается, если F < FО±:K1:K2 .
больше критического FО±:K1:K2, опредеВнленного на уровне значимости О± при числе степеней свободы k1=m-1 и k2=mn-m, и принимается, если F < FО±:K1:K2 .
F- распределение Фишера (для x > 0) имеет следующую функцию плотности (дляВа 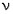 = 1, 2, ..;
= 1, 2, ..; 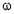 = 1, 2, ..):
= 1, 2, ..):
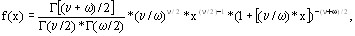
где 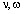 - степени свободы;
- степени свободы;
Г - гамма-функция.
Применительно к данной задаче опровержение гипотезы H0 означает наличие существенных различий в качестве изделий различных партий на рассматриваемом уровне значимости.
Для вычисления сумм квадратов Q1, Q2, Q часто бывает удобно использовать следующие формулы:
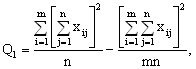 (12)
(12)
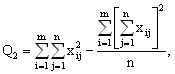 (13)
(13)
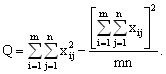 (14)
(14)
т.е. сами средние, вообще говоря, находить не обязательно.
Ва Таким образом, процедура однофакторного дисперсионного анализа состоит в проверке гипотезы H0Вао том, что имеется одна группа однородных экспериментальных данных против альтернативы о том, что таких групп больше, чем одна. Под однородностью понимается одинаковость средних значений и дисперсий в любом подмножестве данных. При этом дисперсии могут быть как известны, так и неизвестны заранее. Если имеются основания полагать, что известная или неизвестная дисперсия измерений одинакова по всей совокупности данных, то задача однофакторного дисперсионного анализа сводится кВа исследованию значимости различия средних в группах данных /1/.
1.3 Многофакторный дисперсионный анализ
Следует сразу же отметить, что принципиальной разницы между многофакторным и однофакторным дисперсионным анализом нет. Многофакторный анализ не меняет общую логику дисперсионного анализа, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного дисперсионного анаВнлиза (в варианте ее компьютерного использования) несомВнненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие /3/.
Общая схема двухфакторного эксперимента, данные коВнторого обрабатываются дисперсионным анализом имеет вид:
Рисунок 1.1 тАУ Схема двухфакторного эксперимента
Данные, подвергаемые многофакторному дисперсионному анализу, часто обозначают в соответствии с количеством факторов и их уровней.
Предположив, что в рассматриваемой задаче о качеВнстве различных m партий изделия изготавливались на разных t станках и требуется выяснить, имеются ли существенные разВнличия в качестве изделий по каждому фактору:
А - партия изВнделий;
B - станок.
В результате получается переход к задаче двухфакторного дисперсионного анализа.
Все данные представлены в таблице 1.2, в котоВнрой по строкам - уровни Ai фактора А, по столбцам тАФ уровни Bj фактора В, а в соответствующих ячейках, таблиВнцы находятся значения показателя качества изделий xijk (i=1,2,..,m; j=1,2,..,l; k=1,2,..,n).
Таблица 1.2 тАУ Показатели качества изделий
Вместе с этим смотрят:
Дифференциальные уравнения I и II порядкаДоказательства теоремЕвклид - жизнь и сочиненияЖенщины-математики