Конус и все, что с ним связано

КОНУС

1. Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг тАУ основанием конуса

               

1. Получение конуса: конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

                       

1. Сечение конуса: если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого тАУ диаметр основания конуса, а боковые стороны тАУ образующие конуса. Это сечение называется осевым.

                    

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О1, расположенной на оси конуса.

                              

1. Площадь поверхности конуса: разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора тАУ длине окружности основания конуса. За площадь боковой поверхности конуса принимается площадь ее развертки.

                                  

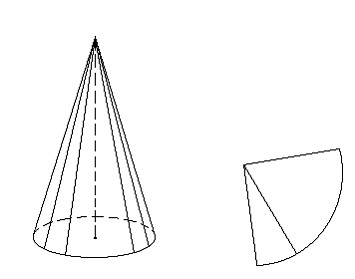
где О± тАУ градусная мера дуги АВА1

       

откуда        

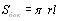
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

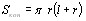
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

1. Усеченный конус, его получение и площадь:

                 

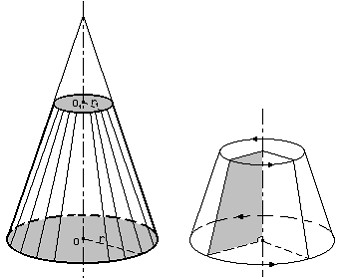
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

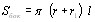
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.

Вместе с этим смотрят:

Корифей математики XIX века - Пафнутий Львович Чебышев
Корни многочленов. Производные и кратные корни
Кривизна плоской кривой. Эволюта и эвольвента
Кривые и поверхности второго порядка