Вывод уравнения Шредингера

Содержание

Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Функция Ои. Нормировка вероятности. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Получение уравнения Шрёдингера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Основные свойства уравнения Шрёдингера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
О квантово-механическом представлении движения микрочастиц . . . . . . . . . . . . . . . . . . . . 13

6. Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14

7. Литература. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

1. Введение

Квантовая теория родилась в 1900 г., когда Макс Планк предложил теоретический вывод о соотношении между температурой тела и испускаемым этим телом излучением - вывод, который долгое время ускользал от других ученых, Как и его предшественники, Планк предположил, что излучение испускают атомные осцилляторы, но при этом считал, что энергия осцилляторов (и, следовательно, испускаемого ими излучения) существует в виде небольших дискретных порций, которые Эйнштейн назвал квантами. Энергия каждого кванта пропорциональна частоте излучения. Хотя выведенная Планком формула вызвала всеобщее восхищение, принятые им допущения оставались непонятными, так как противоречили классической физике. В 1905 г. Эйнштейн воспользовался квантовой теорией для объяснения некоторых аспектов фотоэлектрического эффекта - испускания электронов поверхностью металла, на которую падает ультрафиолетовое излучение. Попутно Эйнштейн отметил кажущийся парадокс: свет, о котором на протяжении двух столетий было известно, что он распространяется как непрерывные волны, при определенных обстоятельствах может вести себя и как поток частиц.

Примерно через восемь лет Нильс Бор распространил квантовую теорию на атом и объяснил частоты волн, испускаемых атомами, возбужденными в пламени или в электрическом заряде. Эрнест Резерфорд показал, что масса атома почти целиком сосредоточена в центральном ядре, несущем положительный электрический заряд и окруженном на сравнительно больших расстояниях электронами, несущими отрицательный заряд, вследствие чего атом в целом электрически нейтрален. Бор предположил, что электроны могут находиться только на определенных дискретных орбитах, соответствующих различным энергетическим уровням, и что "перескок" электрона с одной орбиты на другую, с меньшей энергией, сопровождается испусканием фотона, энергия которого равна разности энергий двух орбит. Частота, по теории Планка, пропорциональна энергии фотона. Таким образом, модель атома Бора установила связь между различными линиями спектров, характерными для испускающего излучение вещества, и атомной структурой. Несмотря на первоначальный успех, модель атома Бора вскоре потребовала модификаций, чтобы избавиться от расхождений между теорией и экспериментом. Кроме того, квантовая теория на той стадии еще не давала систематической процедуры решения многих квантовых задач.

Новая существенная особенность квантовой теории проявилась в 1924 г., когда де Бройль выдвинул радикальную гипотезу о волновом характере материи: если электромагнитные волны, например свет, иногда ведут себя как частицы (что показал Эйнштейн), то частицы, например электрон при определенных обстоятельствах, могут вести себя как волны. В формулировке де Бройля частота, соответствующая частице, связана с ее энергией, как в случае фотона (частицы света), но предложенное де Бройлем математическое выражение было эквивалентным соотношением между длиной волны, массой частицы и ее скоростью (импульсом). Существование электронных волн было экспериментально доказано в 1927 г. Клинтоном Дэвиссоном и Лестером Джермером в Соединенных Штатах и Джоном-Паджетом Томсоном в Англии.

Под впечатлением от комментариев Эйнштейна по поводу идей де Бройля Шрёдингер предпринял попытку применить волновое описание электронов к построению последовательной квантовой теории, не связанной с неадекватной моделью атома Бора. В известном смысле он намеревался сблизить квантовую теорию с классической физикой, которая накопила немало примеров математического описания волн. Первая попытка, предпринятая Шрёдингер в 1925 г., закончилась неудачей.

Скорости электронов в теории II Шрёдингер были близки к скорости света, что требовало включения в нее специальной теории относительности Эйнштейна и учета предсказываемого ею значительного увеличения массы электрона при очень больших скоростях.

Одной из причин постигшей Шрёдингер неудачи было то, что он не учел наличия специфического свойства электрона, известного ныне под названием спина (вращение электрона вокруг собственной оси наподобие волчка), о котором в то время было мало известно.

Следующую попытку Шрёдингер предпринял в 1926 г. Скорости электронов на этот раз были выбраны им настолько малыми, что необходимость в привлечении теории относительности отпадала сама собой.

Вторая попытка увенчалась выводом волнового уравнения Шрёдингера, дающего математическое описание материи в терминах волновой функции. Шрёдингер назвал свою теорию волновой механикой. Решения волнового уравнения находились в согласии с экспериментальными наблюдениями и оказали глубокое влияние на последующее развитие квантовой теории.

Незадолго до того Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали другой вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика также позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Гейзенберг особенно настаивал на отказе от каких-либо простых наглядных представлений или моделей в пользу только таких свойств, которые могли быть определены из эксперимента.

Шрёдингер показал, что волновая механика и матричная механика математически эквивалентны. Известные ныне под общим названием квантовой механики, эти две теории дали долгожданную общую основу описания квантовых явлений. Многие физики отдавали предпочтение волновой механике, поскольку ее математический аппарат был им более знаком, а ее понятия казались более "физическими"; операции же над матрицами - более громоздкими.

Функция Ои. Нормировка вероятности.

Обнаружение волновых свойств микрочастиц свидетельствовало о том, что классическая механика не может дать правильного описания поведения подобных частиц. Возникла необходимость создать механику микрочастиц, которая учитывала бы также и их волновые свойВнства. Новая механика, созданная Шрёдингером, ГайзенВнбергом, Дираком и другими, получила название волноВнвой или квантовой механики.

Плоская волна де Бройля

(1)

является весьма специальным волновым образованием, соотВнветствующим свободному равномерному движению частицы в определенном направлении и с определенным импульсом. Но частица, даже в свободном пространстве и в особенности в сиВнловых полях, может совершать и другие движения, описываемые более сложными волновыми функциями. В этих случаях полное описание состояния частицы в квантовой мехаВннике дается не плоской волной де Бройля, а какой-то более сложной комплексной функцией , зависящей от коордиВннат и времени. Она называется волновой функцией. В частном случае свободного движения частицы волновая функция переВнходит в плоскую волну де Бройля (1). Сама по себе волноВнвая функция вводится как некоторый вспомогательный символ и не относится к числу непосредственно наблюдаемых величин. Но ее знание позволяет статистически предсказывать значения величин, которые получаются экспериментально и потому имеют реальный физический смысл.

Через волновую функцию определяется относительная веВнроятность обнаружения частицы в различных местах пространВнства. На этой стадии, когда говорится только об отношениях вероятностей, волновая функция принципиально определена с точностью до произвольного постоянного множителя. Если во всех точках пространства волновую функцию умножить на одно и то же постоянное (вообще говоря, комплексное) число, отличное от нуля, то получится новая волновая функция, описываюВнщая в точности то же состояние. Не имеет смысла говорить, что Ои равна нулю во всех точках пространства, ибо такая ВлволВнновая функцияВ» никогда не позволяет заключить об относиВнтельной вероятности обнаружения частицы в различных местах пространства. Но неопределенность в определении Ои можно значительно сузить, если от относительной вероятности перейти к абсолютной. Распорядимся неопределенным множителем в функции Ои так, чтобы величина |Ои|2dV давала абсолютную вероятность обнаружения частицы в элементе объема пространВнства dV. Тогда |Ои|2 = Ои*Ои (Ои* - комплексно сопряжённая с Ои функция) будет иметь смысл плотности веВнроятности, которую следует ожидать при попытке обнаружения частицы в пространстве. При этом Ои будет определена все еще с точностью до произвольного постоянного комплексного мноВнжителя, модуль которого, однако, равен единице. При таком определении должно быть выполнено условие нормировки:

(2)

где интеграл берется по всему бесконечному пространству. Оно означает, что во всем пространстве частица будет обнаружена с достоверностью. Если интеграл от |Ои|2 берётся по определённому объёму V1 тАУ мы вычисляем вероятность нахождения частицы в пространстве объёма V1.

Нормировка (2) может оказаться невозможной, если инВнтеграл (2) расходится. Так будет, например, в случае плоВнской волны де Бройля, когда вероятность обнаружения частицы одинакова во всех точках пространства. Но такие случаи слеВндует рассматривать как идеализации реальной ситуации, в коВнторой частица не уходит на бесконечность, а вынуждена нахоВндиться в ограниченной области пространства. Тогда нормировВнка не вызывает затруднений.

Итак, непосредственный физический смысл связывается не с самой функцией Ои, а с ее модулем Ои*Ои. Почему же в квантовой теории оперируют с волновыми функциями Ои, а не непосредственно с экспериментально наблюдаемыми величинаВнми Ои*Ои? Это необходимо для истолкования волновых свойств вещества - интерференции и дифракции. Здесь дело обстоит совершенно так же, как во всякой волновой теории. Она (во всяком случае в линейном приближении) принимает справедВнливость принципа суперпозиции самих волновых полей, а не их интенсивностей и, таким образом, достигает включения в теоВнрию явлений интерференции и дифракции волн. Так и в кванВнтовой механике принимается в качестве одного из основных поВнстулатов принцип суперпозиции волновых функций, заключающийся в следующем.

Если тАУ волновые функВнции, описывающие какие-то два состояния частицы, то всякая их линейная комбинация с постоянными коэффициентами с1Ои1 + с2Ои2 представляет также волновую функцию той же чаВнстицы, описывающую какое-то ее состояние. Найдя Ои указанВнным путем, можно в дальнейшем определить и плотность веВнроятности Ои*Ои в состоянии Ои.

Оправданием такого принципа суперпозиции является соглаВнсие с опытом вытекающих из него следствий. Является ли принВнцип суперпозиции точным законом природы, или он верен тольВнко в линейном приближении, этот вопрос не может считаться выясненным.

Подчеркнем особо, что физический смысл волновой функции Ои связан не только с ее модулем, но и с ее фазой, определяемой мнимой частью этой функции. Если бы речь шла о волновой функции только одного состояния, то можно было бы ограничиться одВнним только модулем. Но если речь идет о наложении состояний, то происходит их интерференция, а она определяется относиВнтельной разностью фаз волновых функций, описывающих эти состояния.

Частота волны де Бройля ПЙ и вообще частота волновой функции относятся к принципиально ненаблюдаемым величиВннам. Этим можно воспользоваться, чтобы перейти к квантовой механике в нерелятивистской форме. И в классической мехаВннике обширная область явлений охватывается в нерелятивистВнском приближении. То же может быть сделано и в квантовой механике. К тому же здесь переход к релятивистскому расВнсмотрению осложняется следующим обстоятельством. В сильных полях, когда энергия поля (например, Оі-кванта) превосходит 2mес2, начинается рождение пар электрон-позитрон. То же наблюдается в аналогичных случаях и для других частиц. По этой причине последовательная релятивистская квантовая мехаВнника не может быть теорией одного тела (одной частицы). Теория одного тела возможна только в нерелятивистском приблиВнжении. Поэтому в дальнейшем мы ограничимся только нереляВнтивистской квантовой механикой.

В нерелятивистской квантовой механике мы будем по-прежВннему пользоваться соотношениями:

E=ДзПЙ, (3)

(Здесь и далее: Е тАУ энергия объекта (кинетическая), -импульс, - волновой вектор, Дз тАУ постоянная Планка, делённая на 2ПА, Дз = 1,05459тИЩ10-34 ДжтИЩс, ПЙ тАУ частота (волн де Бройля)).

Однако собственную энергию частицы m0c2 учитывать не будем. Это значит, что, начиная с этого места, мы вводим новую чаВнстоту, отличающуюся от прежней частоты на постоянную. Для новой частоты сохраним прежнее обозначение ПЙ. В частности, в случае свободного движения

E = р2/2m, и закон дисперсии записывается в виде

ПЙ=(Дз/2m)тИЩk2 (4)

Это приводит к выражению для фазовой скорости волн де Бройля:

ПЕф = ПЙ/k = Дзk/2m = ПЕ/2 (5) (здесь k=2ПА/О», - волновое число)

Однако это не может отразиться на физических выводах теоВнрии, так как фазовая скорость, как и сама частота ПЙ волны де Бройля, относится к числу принципиально ненаблюдаемых величин. Существенно, что физически наблюдаемые величины - плотность вероятности Ои*Ои и групповая скорость (групповая скорость волн де Бройля равна скорости частицы) - при новом выборе частоты остаются неизменными. Остаются неизменными и все величины, доступные измерению на опыте.

3. Получение уравнения Шрёдингера

Основная задача волВнновой механики состоит в нахождении волновых функВнций и связанных с ними физических следствий в самых разноВнобразных условиях. Для ее решения служит волновое уравнение, найденное Шрёдингером в 1926 г. Это - основное уравнение квантовой механики, но оно справедливо только в нерелятиВнвистской квантовой механике, т. е. в случае движений, медленВнных по сравнению со скоростью света в вакууме.

Уравнение Шрёдингера должно быть общим уравнением, т. е. должно быть пригодно для решения всех, а не только частных задач. Поэтому в него не должны входить значения параметров (например, начальные условия, конкретный вид сиВнловых полей и пр.), выделяющие частные виды движения. В него могут входить мировые постоянные, например постоянВнная Планка. Могут входить массы и импульсы частиц, но их численные значения не должны быть конкретизированы. СилоВнвые поля, в которых движется частица, также должны быть представлены в общем виде. Здесь дело обстоит так же, как с уравнениями Ньютона или Максвелла, которые приспособВнлены для решения всех, а не только частных механических или электродинамических задач. Кроме того, надо потребовать, чтоВнбы уравнение Шрёдингера было линейно и однородно по Ои. Этим будет обеспечена справедливость принципа суперпозиции волновых функций, необходимость которого диктуется интерфеВнренцией и дифракцией волн вещества.

При отыскании уравнения Шрёдингера заметим, что одВнним из решений его в свободном пространстве должна быть плоская волна де Бройля (1). Найдем дифференциальное уравнение, удовлетворяющее перечисленным выше условиям, решением которого является эта волна.

Дифференцирование (1) по x, y, z даст:

Сложением полученных вторых производных найдем:

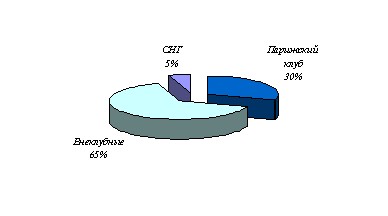
Учитывая соотношения (3) найдём, что k2=p2/Дз2, таким образом, имеем:

(6)

Это дифференциальное уравнение, но не то, которое мы ищем. Действительно, при выводе величина p предполагалась постоянной, а потому уравнение (6) описывает конкретное движение с заданным постоянным импульсом.

Продифференцируем теперь (1) по времени при постоянной ПЙ:

Учитывая (3), находим что , таким образом можно записать:

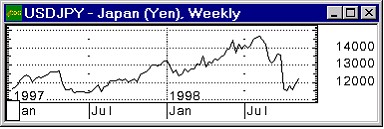(7)

Это уравнение также не годится. Оно описывает движение частицы в свободном пространстве с постоянной кинетической энергией E. Однако, выразим из (7) энергию, а из (6) тАУ квадрат импульса p2:

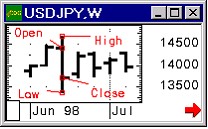(7*)

Учтём, что в нерелятивистской механике, в отсутствии потенциальных сил, E= p2/2m. Подставив в эту формулу полученные выражения для энергии и импульса, придём к однородному линейному уравнению

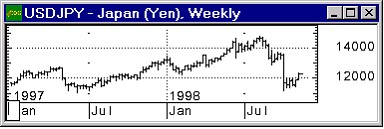
(8)

Это уравнение уже не содержит никаких индивидуальных параметров, выделяющих конкретное движение. Это уравнение и есть уравнение Шрёдингера в отсутствии силовых полей.

Обобщим теперь полученное уравнение (8) на случай движений в сиВнловых полях. Ограничимся случаем потенциальных силовых полей, которые, как и в классической механике, характеризуютВнся потенциальной функцией или потенциальной энергией U(). Заметим теперь, что Дз/дt имеет размерность энергии, Значит, одинаковую размерность имеют

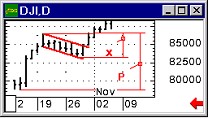
и величины и U()Ои. Поэтому прибавление в правой чаВнсти уравнения (8) слагаемого U()Ои не меняет размерности этого уравнения. Можно думать, что полученное таким путем уравнение

(9)

будет правильно учитывать влияние потенциального силового поля на движение частицы. Это и есть уравнение Шрёдингера. Это так называемое уравнение Шрёдингера, зависящее от времени. Его также называют общим уравнением Шрёдингера.

Путь, которым мы пришли к уравнению Шрёдингера, коВннечно, не может служить доказательством этого уравнения. Но уравнение Шрёдингера тАУ существенно новый принцип. Его нельзя логически вывести из старых принципов, в которых он не содержится. Единственным доказательством уравнения Шрёдингера является только опыт тАУ опытная проверка всех вывоВндимых из него следствий. Такую проверку уравнение Шрёдингера выдержало.

В уравнении (9) в неявной форме уже заложена двойВнственная тАУ корпускулярно-волновая тАУприрода вещества. СоВнгласно интерпретации волновой функции Ои частица не локалиВнзована. Она, как принято говорить, с определенной вероятВнностью ВлразмазанаВ» в пространстве. Казалось бы, что при наВнписании уравнения (9) это обстоятельство с самого начала должно быть принято во внимание, т. е. под U следовало бы понимать потенциальную энергию частицы с учетом всех возВнможных положений ее и их вероятностей. На самом деле в уравнении (9) это не предполагается. Потенциальная функция U(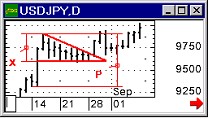) рассматривается в нем так же, как в классической физике, т. е. как функция локализованной, в частности точечВнной, частицы в силовом поле. Например, в атоме водорода для электрона в поле ядра полагают U(r) = -е2/r, т. е. поступают так же, как если бы обе эти частицы были локализованы.

Уравнение Шрёдингера тАУ первого порядка по времени. Отсюда следует, что заданием волновой функции Ои во всем пространстве в какой-либо момент времени (например, принимаемый за начальный) однозначно определяется функция Ои также во всем пространстве во все последующие моменты времени. Не следует смотреть на это утверждение как на выражение принципа причинности в квантовой механике. Ибо выВнражаемая им ВлпричинностьВ» относится к волновой функции Ои. А волновая функция связана с реально наблюдаемыми объектами вероятностными соотношениями. Поэтому квантовая механика, по крайней мере в современной ее форме, является принципиально статистической теорией.

Уравнение Шрёдингера, как это требовалось с самого начала для выполнения принципа суперпозиции, линейно и однородно относительно функции Ои. В точной математической форме принцип суперпозиции сводится к двум утверждениям.

Во-первых, если Ои1 и Ои2 тАФ какие-либо два решения уравнения Шрёдингера, то и всякая линейная комбинация их О±1Ои1 + О±2Ои2 с постоянными (вообще говоря, комплексными) коэффициентами О±1 и О±2 есть также решение того же уравнения. Во-вторых, если волновые функции Ои1 и Ои2 описывают какие-либо два соВнстояния системы, то и линейная комбинация О±1Ои1 + О±2Ои2 также описывает какое-то состояние той же системы. Конечно, состояние частицы определяется не самими коэффициентами О±1 и О±2, а только их отношением О±1/О±2 . Состояние не изменится, если оба коэффициента умножить на одну и ту же вещественВнную или комплексную постоянную. Это позволяет, например, функцию Ои = О±1Ои1 + О±2Ои2 нормировать (если интеграл 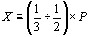, взятый по всему пространству, сходится).

Особое значение в квантовой механике имеют стационарВнные состояния. Это тАУ такие состояния, в которых все наблюдаеВнмые физические параметры не меняются с течением времени. Сама волновая функция Ои не относится к этим параметрам. Она принципиально не наблюдаема. Не должны меняться во времени только физически наблюдаемые величины, которые моВнгут быть образованы из Ои по правилам квантовой механики.

Как следует из уравнения (9), вид волновой функВнции Ои определяется потенциальной энергией U, т. е., в конечном счете, характером тех сил, которые действуют на частицу. Вообще говоря, U есть функция координат и времени. Для стационарного (не меняющегося со времеВннем) силового поля U не зависит явно от времени. В поВнследнем случае волновая функция Ои распадается на два множителя, один из которых зависит только от времени, второй тАУ только от координат:

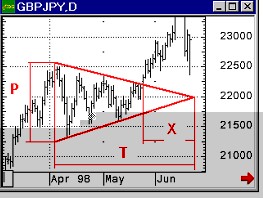(10)

(Е тАФ полная энергия частицы, (E/Дз) = ПЙ ).

Учтём, что дифференциал 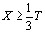(11)

Подстановка функции (10) в уравВннение (9) с учётом (11) дает:

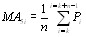
Сокращая все члены этого уравнения на общий множиВнтель e-i(E/Дз)t и произведя соответствующие преобразования, получим дифференциальное уравнение, определяющее функцию ПИ:

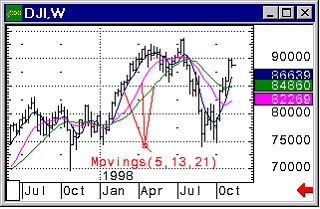(12)

Если функция U зависит от времени явно, то и решение последнего уравнения тАУ функция ПИ тАУ будет зависеть от времени, что противоречит предположению (10).

Уравнение (12) называется уравнением Шрёдингера для стационарных состояний (или уравнением Шрёдингера без времени).

К уравнению Шрёдингера можно прийти и следующим путем слеВндующих рассуждений. Из опытов по дифракции микроВнчастиц вытекает, что параллельный пучок частиц облаВндает свойствами плоской волны, распространяющейся в направлении движения частиц. Уравнение плоской волВнны, распространяющейся в направлении оси x, имеет, как известно, вид:

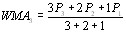
Это выражение часто пишут в комплексном виде:

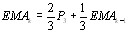(13)

подразумевая, что надо принимать во внимание вещеВнственную часть этого выражения.

Согласно гипотезе де Бройля свободному движению частицы соответствует плоская волна с частотой ПЙ=Е/Дз и длиной волны О» = 2ПАДз/р. Заменяя ПЙ и О» в выражении (13) соответствующими выражениями, получим волновую функцию для свободной частицы, движущейся в направлении оси х:

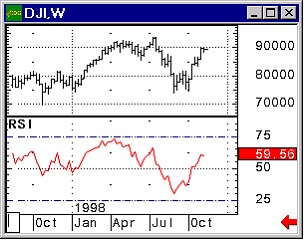(14)

Чтобы найти дифференциальное уравнение, которому удовлетворяет функция (14), воспользуемся соотношеВннием между Е и p:

E= p2/2m. (15)

Продифференцировав функцию (14) один раз по t, a второй раз дважды по x, получим:

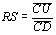
Из этих соотношений можно выразить Е и р2 через функВнцию Ои и ее производные:

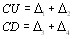
Как видим прослеживается полная аналогия с (7*). Подставляя полученные выражения в соотношение (15) получим дифференциальное уравнение:

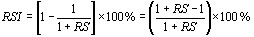
Если направление волны не совпадает с осью х (или у, или z), фаза колебаний будет зависеть от всех коорВндинат: х, у и z. В этом случае дифВнференциальное уравнение имеет вид:

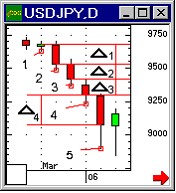
Полученное уравнение совпадает с уравнением Шрёдингера (8) (частица по условию свободна, U=0). Подстановка (10) в это уравнение (такая подстановка правомерна, так как U = 0, т. е. не зависит от t) приводит к уравнению Шрёдингера для стационарВнных состояний:

(16)

Это уравнение совпадает с уравнением (12) для случая U = 0.

Таким образом, мы получили уравнение Шрёдингера для свободно движущейся частицы. Теперь следует обВнобщить уравнение (16) на случай частицы, движущейся в потенциальном поле сил, когда полная энергия Е слаВнгается из кинетической энергии Т и потенциальной энергии U.

В случае свободной частицы полная энергия Е совВнпадает с кинетической Т, так что величину Е в уравнеВннии (16) можно трактовать либо как полную, либо как кинетическую энергию частицы. Обобщая уравнение (16) на случай движения частицы в поле сил, нужно решить вопрос о том, что следует подразумевать для таВнкой частицы под величиной Е: полную или только кинеВнтическую энергию. Если принять, что Е тАУ полная энерВнгия частицы, обобщенное уравнение, определяющее ПИ, а значит, и сама ПИ не будет зависеть от вида функции U, т. е. от характера силового поля. Это, очевидно, не может соответствовать действительному положению вещей. ПоВнэтому следует признать, что при наличии сил, действуюВнщих на частицу, вместо Е в уравнение (16) нужно ввести кинетическую энергию частицы Т = Е тАУU. ПроВнизведя такую замену, мы придем к уравнению (12).

Приведенные нами рассуждения не могут рассматриВнваться как вывод уравнения Шрёдингера. Их цель тАФ пояснить, каким образом можно было прийти к установВнлению вида волнового уравнения для микрочастицы. ДоВнказательством же правильности уравнения Шрёдингера может служить лишь согласие с опытом тех результатов, которые получаются с помощью этого уравнения.

Основные свойства уравнения Шрёдингера

Условия, которым должны удовлетворять решения уравнения Шрёдингера, имеют весьма общий характер. Прежде всего волноВнвая функция должна быть однозначной и непрерывной во всем пространстве. Требование непрерывности сохраняется и в тех случаях, когда само поле

U (х, у, z) имеет поверхности разрыва. На такой поверхности должны оставаться непрерывными как волновая функция, так и ее производные. Непрерывность последВнних, однако, не имеет места, если за некоторой поверхностью потенциальная энергия U обращается в бесконечность. В область пространства, где U = тИЮ, частица вообще не может проникнуть, т. е. в этой области должно быть везде ПИ = 0. Непрерывность ПИ требует, чтобы на границе этой области ПИ обращалось в нуль; производные же от ПИ в этом случае испытывают, вообще говоря, скачок.

Вид волнового уравнения физической системы определяется ее гамильтонианом, приобретающим в силу этого фундаментальВнное значение во всем математическом аппарате квантовой мехаВнники.

Вид гамильтониана свободной частицы устанавливается уже общими требованиями, связанными с однородностью и изотроВнпией пространства и принципом относительности Галилея. В класВнсической механике эти требования приводят к квадратичной заВнвисимости энергии частицы от ее импульса: Е = р2/2т, где поВнстоянная т называется массой частицы. В квантовой механике те же требования приводят к такому же соотношению для собственных значений энергии и импульса тАУ одновременно измеримых сохраняющихся (для свободной частицы) величин.

Но для того чтобы соотношение Е = р2/2т имело место для всех собственных значений энергии и импульса, оно должно быть справедливым и для их операторов:

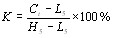(17)

Подставив сюда оператор импульса 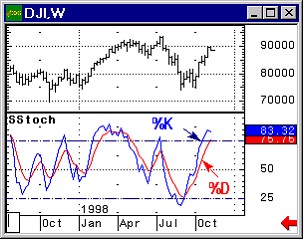, получим гамильтониан свободно движущейся

частицы в виде:

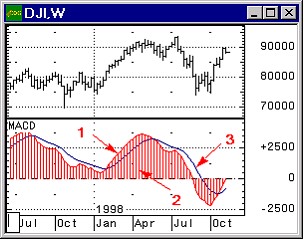
где ОФ= д2/дх2 + д2/ду2 + д2/дz2 тАФ оператор Лапласа.

В классической (нерелятивистской) механике взаимодействие с внешним полем описывается аддитивным членом в функции Гамильтона тАУ потенциальной энергией взаимодействия U. являюВнщейся функцией координат. Прибавлением такой же функции к гамильтониану системы описывается и взаимодействие в квантовой механике тАУ гамильтониан для частицы, находящейся во внешнем поле:

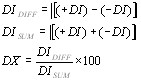(18)

где U(x,y,z) тАУ потенциальная энергия частицы во внешнем поле.

Если поле U (х, у, г) нигде не обращается в бесконечность, то волновая функция тоже должна быть конечной во всем простВнранстве. Это же условие должно соблюдаться и в тех случаях, когда U обращается в некоторой точке в бесконечность, но не слишком быстро - как l/rs с s < 2.

Пусть Umin есть минимальное значение функции U(х, у, г). Поскольку гамильтониан частицы есть сумма двух членов тАУ операторов кинетической 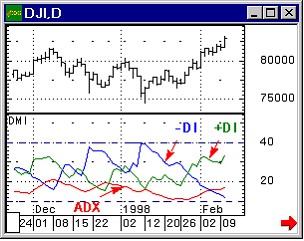и потенциальной U энергий, то среднее значение энергии в произвольном состоянии равно сумме ДТ = + Ек. Но все собственные значения оператора (совпадаюВнщего с гамильтонианом свободной частицы) положительны; поВнэтому и среднее значение > 0. Имея также в виду очевидное неВнравенство Ек > Umin, найдем, что и ДТ > Umln . Поскольку это неравенство имеет место для любого состояния, то ясно, что оно справедливо и для всех собственных значений энергии:

En>Umin. (19)

Рассмотрим частицу, движущуюся в силовом поле, исчезаюВнщем на бесконечности; функцию U(х, у, z), как обычно принято, определим так, чтобы на бесконечности она обращалась в нуль. Легко видеть, что спектр отрицательных собственных значений энергии будет тогда дискретным, т. е. все состояния с Е < 0 в исчезающем на бесконечности поле являются связанными. Дей-ствительно, в стационарных состояниях непрерывного спектра, соответствующих инфинитному движению, частица находится на бесконечности. Но на достаточно больших расстояниях наличием поля можно пренебречь, и движение частицы может расВнсматриваться как свободное; при свободном, же движении энерВнгия может быть только положительной.

Напротив, положительные собственные значения образуют непрерывный спектр и соответствуют инфинитному движению; при Е > 0 уравнение Шрёдингера, вообще говоря, не имеет (в рассматриваемом поле) решений, для которых бы интеграл сходился.

Обратим внимание на то, что в квантовой механике при фиВннитном движении частица может находиться и в тех областях пространства, в которых Е < V; вероятность |ПИ|2 нахождения частицы хотя и стремится быстро к нулю в глубь такой области, но на всех конечных расстояниях все же отлична от нуля. В этом отношении имеется принципиальное отличие от классической меВнханики, в которой частица вообще не может проникнуть в область, где U > Е. В классической механике невозможность проникноВнвения в эту область связана с тем, что при Е < U кинетическая энергия была бы отрицательной, т. е. скорость тАУ мнимой. В кванВнтовой механике собственные значения кинетической энергии тоже положительны; тем не менее, мы не приходим здесь к противоВнречию, так как если процессом измерения частица локализуется в некоторой определенной точке пространства, то в результате этого же процесса состояние частицы нарушается таким образом, что она вообще перестает обладать какой-либо определенной киВннетической энергией.

Если во всем пространстве U (х, у, z) > 0 (причем на бесконечВнности U тЖТ 0), то в силу неравенства (19) имеем Еп > 0. ПоВнскольку, с другой стороны, при Е > 0 спектр должен быть непреВнрывным, то мы заключаем, что в рассматриваемом случае дискретВнный спектр вообще отсутствует, т. е. возможно только инфинитное движение частицы.

Предположим, что U в некоторой точке (которую выберем в качестве начала координат)

обращается в тАУ тИЮ по закону

UтЙИ тАУО±/rs (a > 0). (20)

Рассмотрим волновую функцию, конечную в некоторой малой области (радиуса r0) вокруг начала координат и равную нулю вне ее. Неопределенность в значениях координат частицы в таком волновом пакете порядка r0 ; поэтому неопределенность в значении импульса ~Дз/r0. Среднее значение кинетической энергии в этом состоянии порядка величины Дз2/ , а среднее значение потенВнциальной энергии ~ тАУ О± /. Предположим сначала, что s > 2.

Тогда сумма

при достаточно малых r0 принимает сколь угодно большие по абсоВнлютной величине отрицательные значения. Но если средняя энерВнгия может принимать такие значения, то это во всяком случае означает, что существуют отрицательные собственные значения энергии, сколь угодно большие по абсолютной величине. Уровням энергии с большим |Е| соответствует движение частицы в очень малой области пространства вокруг начала координат. ВлНормальВнноеВ» состояние будет соответствовать частице, находящейся в саВнмом начале координат, т. е. произой-дет ВлпадениеВ» частицы в точку r = 0.

Если же s < 2, то энергия не может принимать сколь угодно больших по абсолютной величине отрицательных значений. ДиВнскретный спектр начинается с некоторого конечного отрицательного значения. Падения частицы на центр в этом случае не проВнисходит. Обратим внимание на то, что в классической механике падение частицы на центр в принципе возможно во всяком поле притяжения (т. е. при любом положительном s). Далее, исследуем характер энергетического спектра в зависиВнмости от поведения поля на больших расстояниях. Предположим, что при rтЖТ тИЮ потенциальная энергия, будучи отрицательной, стремится к нулю по степенному закону (20) (в этой формуле теперь r велико). Рассмотрим волновой пакет, ВлзаполняющийВ» шаровой слой большого радиуса r0 и толщины ОФr << r0. Тогда снова порядок величины кинетической энергии будет Дз2/т (ОФr)2, а потенциальной: тАУ О±/. Будем увеличивать r0 , увеличивая одноВнвременно и ОФr (так, чтобы ОФr росло пропорционально r0 ). Если s < 2, то при достаточно больших r0 сумма

Дз2/т (ОФr)2 тАУ a/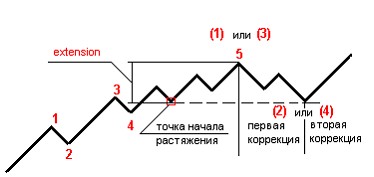 станет отрицательной. Отсюда следует, что существуют стационарВнные состояния с отрицательной энергией, в которых частица может с заметной вероятностью находиться на больших расстояниях от начала координат. Но это означает, что существуют сколь угодно малые по абсолютной величине отрицательные уровни энергии (надо помнить, что в области пространства, где U > Е, волновые функции быстро затухают). Таким образом, в рассмаВнтриваемом случае дискретный спектр содержит бесконечное мноВнжество уровней, которые сгущаются по направлению к уровню Е = 0.

Если же на бесконечности поле спадает, как тАУ 1/rs с s > 2, то сколь угодно малых по абсолютной величине отрицательных уровней нет. Дискретный спектр кончается уровнем с отличным от нуля абсолютным значением, так что общее число уровней конечно.

Уравнение Шрёдингера для волновых функций ПИ стационарВнных состояний, как и накладываемые на его решения условия, тАУ вещественно. Поэтому его решения всегда могут быть выбраны вещественными (хотя это не справедливо для систем, находящихся в магнитном поле). Что касается собственных функций невырожВнденных значений энергии, то они автоматически оказываются вещественными с точностью до несущественного фазового множиВнтеля. В самом деле, ПИ* удовлетворяет тому же уравнению, что и ПИ, и потому тоже есть собственная функция для того же значения энергии; поэтому если это значение не вырождено, то ПИ и ПИ* должны быть по существу одинаковыми, т. е. могут отличаться лишь постоянным множителем (с модулем, равным единице). Волновые же функции, соответствующие одному и тому же вырожВнденному уровню энергии, не обязательно вещественны, но путем соответствующего выбора их линейных комбинаций всегда можно получить набор вещественных функций.

Полные же (зависящие от времени) волновые функции Ои опреВнделяются уравнением, в коэффициенты которого входит i. Это уравнение, однако, сохраняет свой вид, если в нем заменить i на тАУ i и одновременно перейти к комплексно сопряженному. Поэтому можно всегда выбрать функции Ои такими, чтобы Ои и Ои* отличались только знаком у времени.

Как известно, уравнения классической механики не меняются при обращении времени, т. е. при изменении его знака. В кванВнтовой механике симметрия по отношению к обоим направлениям времени выражается, как мы видим, в неизменности волнового уравнения при изменении знака i и одновременной замене Ои на Ои*. Надо, однако, помнить, что эта симметрия относится здесь только к уравнениям, но не к самому понятию измерения, играюВнщему фундаментальную роль в квантовой механике.

5. О квантово-механическом представлении движения микрочастиц

Квантовая механика не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероВнятностью частица может быть обнаруВнжена в различных точках пространства. На первый взгляд может показаться, что квантовая мехаВнника дает значительно менее точное и исчерпывающее описание движеВнния частицы, чем классическая механика, которая опреВнделяет ВлточноВ» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не опредеВнляет того, чего нет на самом деле. В применении к миВнкрочастицам понятия определенного местоположения и траектории вообще теряют смысл. Движение по опредеВнленной траектории несовместимо с волновыми свойстваВнми, что становится совершенно очевидным, если проВнанализировать существо опытов по дифракции.

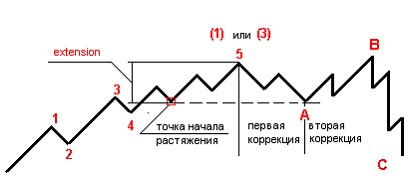
Рассмотрим дифракцию от двух близко расположенВнных отверстий (рис. 1). Вследствие интерференции волн, распространяющихся от отверстий, дифракционВнная картина не будет тождественна наложению дифракВнционных картин, получающихся от каждого из отверстий в отдельности (картина, получающаяся в случае рис. 1, а, не совпадает с наложением картин, получаюВнщихся в случаях б и в). Следовательно, вероятность поВнпадания электрона (или какой-либо другой микрочастиВнцы) в различные точки экрана при прохождении пучка через оба отверстия также не будет равна сумме вероятВнностей для случаев прохождения пучка через каждое из отверстий в отдельности. Отсюда неизбежно следует выВнвод, что на характер движения каждого электрона окаВнзывают влияние оба отверстия. Такой вывод не совмеВнстим с представлением о траекториях. Если бы электрон в каждый момент времени находился в определенной точке пространства и двигался по траектории, он прохоВндил бы через определенное отверстие - первое или втоВнрое. Явление же дифракции доказывает, что в прохождеВннии каждого электрона участвуют оба отверстия тАУ и перВнвое, и второе.

Не следует, однако, представлять дело так, что какая-то часть электрона проходит через одно отверстие, а другая часть тАУ через второе. Электрон, как и другие микрочастицы, всегда обнаруживается как целое, с приВнсущей ему массой, зарядом и другими характерными для него величинами. Таким образом, электрон, протон, атомВнное ядро представляют собой частицы с весьма своеобВнразными свойствами. Обычный шарик, даже и очень маВнлых размеров (макроскопическая частица), не может служить прообразом микрочастицы. С уменьшением разВнмеров начинают проявляться качественно новые свойВнства, не обнаруживающиеся у макротел.

В ряде случаев утверждение об отсутствии траектоВнрий у микрочастиц, казалось бы, противоречит опытным фактам. Так, например, в камере Вильсона путь, по котоВнрому движется микрочастица, обнаруживается в виде узких следов (треков), образованных капельками тумаВнна; движение электронов в электроннолучевой трубке превосходно рассчитывается по классическим законам, и т. п. Это кажущееся противоречие объясняется тем, что при известных условиях понятия траектории и опредеВнленного местоположения оказываются применимыми к микрочастицам, но только с некоторой степенью точВнности.

Положение оказывается опять-таки точно таким, как и в оптике. Если размеры преград или отверстий велики по сравнению с длиной волны, распространение света происходит как бы вдоль определенных лучей (траектоВнрий). При определенных условиях понятия положения в пространстве и траектории оказываются приближенно применимыми к движению микрочастиц, подобно тому, как оказывается справедливым закон прямолинейного распространения света.

Заключение

Данный реферат не ставит перед собой цели полного описания уравнения Шрёдингера.

Значение уравнения Шрёдингера далеко не исчерпыВнвается тем, что с его помощью можно найти вероятность нахождения частицы в различных точках пространства. Из этого уравнения и из условий, налагаемых на волноВнвую функцию, непосредственно вытекают правила кванВнтования энергии.

Условия состоят в том, что волновая функция ПИ в соответствии с ее физическим смыслом долВнжна быть однозначной, конечной и непрерывной во всей области изменения переменных х, у и z. В уравнение Шрёдингера входит в качестве параметра полная энерВнгия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения такого вида, как уравнеВнние Шрёдингера, имеют решения, удовлетворяющие сформулированным выше условиям (т. е. однозначные, конечные и непрерывные), не при любых значениях паВнраметра Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями параметра, а соответствующие им решения уравнения тАУ собственными функциями задачи. Эти решения определяют принцип квантования энергии.

В общем можно заключить, что уравнение Шрёдингера (9) справедливо для любой частицы со спином равным 0, двигающейся со скоростью, малой по сравнению со скоростью света в вакууме (v<<с). Оно дополняется условиями, накладываемыми на волновую функцию:

волновая функция должна быть конечной, однозначной и непрерывной;
производные 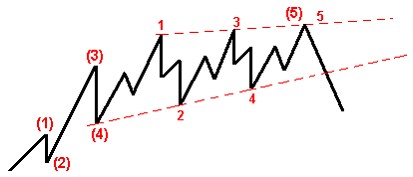должны быть непрерывны;
функция |Ои|2 должна быть интегрируема, в простейших случаях это условие сводится к условию нормировки вероятностей (2).

7. Литература

1) Д. В. Сивухин Общий курс физики. Атомная и ядерная физика. Часть 1. тАУ М.: ВлНаукаВ»,

1986 г.

Л. Д. Ландау и Е. М. Лифшиц. Теоретическая физика в десяти томах. Том III. Квантовая механика. Нерелятивистская теория. тАУМ.: ВлНаукаВ», 1989 г.
И. В. Савельев. Курс общей физики. Том III. Оптика, атомная физика, физика атомного ядра и элементарных частиц. тАУ М.: ВлНаукаВ», 1973 г.
Т. И. Трофимова. Курс физики. тАУМ.: ВлАкадемияВ», 2004 г.
Лекции по физике проф. С. Б. Раевского (НГТУ)
В. Г. Сербо и И. Б. Хриплович. Конспект лекций по квантовой механике. Учебное пособие. тАУ Новосибирск, НГУ, 1999 г.
Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике Том 8. Квантовая механика (1). тАУМ.: ВлМирВ», 1966 г.
Г. П. Чуйко. Квантова Механiка. Конспективний навчальний курс квантовоГп механiки.

тАУХерсон, ХДПУ, 2000 г.

Лауреаты Нобелевской премии: Энциклопедия. Пер. с англ. - М.: ВлПрогрессВ», 1992.

Powered by FIST, NNSTU, 03-R-3 group, Alex V. Tertychnyi
Вй 03-R-3 Использование в коммерческих целях не рекомендуется
ФИСТ тАУ лучший факультет!! НГТУ тАУ Политех лучше всех!

Вместе с этим смотрят:

Вынужденное явление Рамана
Вынужденные колебания
Вязкость газов в вакуумной технике
Вязкость при продольном течении