Консолидирование задолженности

Тюменский Государственный Нефтегазовый Университет

Контрольная работа по дисциплине:

ВлФинансовая математикаВ»

Выполнил ст. гр. МО1с

Калачев С.А.

Тюмень 2002

Содержание

1. Простые и сложные проценты. Сущность и применениетАжтАжтАжтАжтАжтАжтАж.3

2. Консолидирование задолженноститАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж.9

Список литературытАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж15
1. Простые и сложные проценты. Сущность и применение.

Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка вреВнмени. Поскольку стандартным временным интервалом в финанВнсовых операциях является 1 год, наиболее распространен вариВнант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления:

схема простых процентов;

схема сложных процентов.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р; требуемая доходность тАФ г (в долях единицы). Считается, что инвестиция сделана на условиях простого проценВнта, если инвестированный капитал ежегодно увеличивается на величину Р тАв г. Таким образом, размер инвестированного капитаВнла через n лет (Rn) будет равен:

Rn = Р + Р тАв г + тАж+ Р тАв г = P тАв (1 + n тАв r ). (1)

Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходВнной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные, и невостребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляютВнся проценты, все время возрастает. Следовательно, размер инВнвестированного капитала будет равен:

к концу первого года: F1 = Р + Р тАв г = Р тАв (1 + г);

к концу второго года: F2 = F1+ F1 тАв г = F1тАв (1 + г) == Р тАв (1 + г);

к концу n-го года: Fn == Р тАв (1 + г) .

При проведении финансовых операций чрезвычайно важно знать как соотносятся величины Rn и Fn. Все зависит от величины n. С помощью метода математической индукции легко показать, что при n > 1, (1 + г)" > 1 + +п тАв г. Итак,

Rn > Fn, при 0 < n <1;

Fn > Rn, при n >1.

Взаимосвязь Fn и Rn можно представить в виде графика(рис. 1).

Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

более выгодной является схема простых процентов, если срок ссуды менее одного года, (проценты начисляются однократно в конце периода);

более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

обе схемы дают одинаковые результаты при продолжительВнности периода 1 год и однократном начислении процентов.

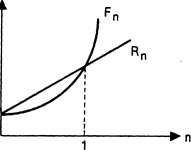
Рис. 1. Простая и сложная схемы наращения капитала

Использование в расчетах сложного процента в случае многоВнкратного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

Формула сложных процентов является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя FMl (r, n), называемого мульВнтиплицирующим множителем и обеспечивающего наращение стоимости, табулированы для различных значений г и n. Тогда формула алгоритма наращения по схеме сложных процентов переписывается следующим образом:

Fn = P тАв FMl (r, n), (2)

где FMl (r, n) = (1 + г) тАФ мультиплицирующий множитель.

Экономический смысл множителя FMl (r, n) состоит в следуВнющем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т.п.) через n периодов при заданной процентной ставке г.

В практических расчетах для наглядной и быстрой оценки эффективности предлагаемой ставки наращения при реализации схемы сложных процентов пользуются приблизительным расчеВнтом времени, необходимого для удвоения инвестированной сумВнмы, известным как Влправило 72-хВ». Это правило заключается в следующем: если г тАФ процентная ставка, выраженная в проценВнтах, то k = 72/r представляет собой число периодов, за которое исходная сумма приблизительно удвоится. Это правило хорошо срабатывает для небольших значений г (до 20%). Так, если годовая ставка г = 12%, то k = 6 годам. Речь идет о периодах начисления процентов и соответствующей данному периоду ставке, а именно, если базовым периодом, т.е. периодом наращения, является квартал, то в расчете должна использоваться квартальная ставка.

Схема простых процентов используется в практике банковсВнких расчетов при начислении процентов по краткосрочным ссуВндам со сроком погашения до одного года. В этом случае в качестве показателя n берется величина, характеризующая удельВнный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округляться: месяц тАФ 30 дней; квартал тАФ 90 дней; полугодие тАФ 180 дней; год тАФ 360 (или 365) дней.

На практике многие финансовые операции выполняются в рамках одного года, при этом могут использоваться различные схемы и методы начисления процентов. В частности, большое распространение имеют краткосрочные ссуды, т.е. ссуды, предоВнставляемые на срок до одного года с однократным начислением процентов. В этом случае для кредитора, диктующего чаще всего условия финансового контракта, более выгодна схема простых процентов, при этом в расчетах исВнпользуют промежуточную процентную ставку, которая равна доле годовой ставки, пропорциональной доле временного инВнтервала в году.

F = Р тАв (1 + F тАвr ), или F = Р тАв (1 + t/TтАв r), (3)

где г тАФ годовая процентная ставка в долях единицы;

t тАФ продолжительность финансовой операции в днях;

Т тАФ количество дней в году;

f тАФ относительная длина периода до погашения ссуды.

При определении продолжительности финансовой операции принято день выдачи и день погашения ссуды считать за один день. В зависимости от того, чему берется равной продолжительВнность года (квартала, месяца), размер промежуточной процентВнной ставки может быть различным. Возможны два варианта:

точный процент, определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

обыкновенный процент, определяемый исходя из приближенВнного числа дней в году, квартале и месяце (соответственно 360, 90, 30).

При определении продолжительности периода, на который выдана ссуда, также возможны два варианта:

принимается в расчет точное число дней ссуды (расчет ведется по дням);

принимается в расчет приблизительное число дней ссуды (исВнходя из продолжительности месяца в 30 дней). Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами (одна для обычного года, вторая для високосного), в которых все дни в году последоВнвательно пронумерованы. Продолжительность финансовой опеВнрации определяется вычитанием номера первого дня из номера последнего дня.

В случае, когда в расчетах используется точный процент, берется и точная величина продолжительности финансовой опеВнрации; при использовании обыкновенного процента может приВнменяться как точное, так и приближенное число дней ссуды. Таким образом, расчет может выполняться одним из трех споВнсобов:

обыкновенный процент с точным числом дней (применяется в Бельгии, Франции);

обыкновенный процент с приближенным числом дней (ФРГ, Дания, Швеция);

точный процент с точным числом дней (Великобритания, США).

В практическом смысле эффект от выбора того или иного способа зависит от значительности суммы, фигурирующей в процессе финансовой операции.

Другой весьма распространенной операцией краткосрочного характера, для оценки которой используются рассмотренные формулы, является операция по учету векселей банком. В этом случае пользуются дисконтной ставкой. Одна из причин состоит в том, что векселя могут оформляться по-разному, однако чаще всего банку приходится иметь дело с суммой к погашению, т.е. с величиной FV. Схема действий в этом случае может быть следуВнющей. Владелец векселя на сумму FV предъявляет вексель банку, который соглашается его учесть, т.е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называВнется дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую исходя из объявленной банком ставки дисконВнтирования (d). Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Расчет предоставляемой банком суммы ведется по формуле:

PV == FV тАв (1 тАФf тАв d ), или PV = FV (1 тАФt/T тАв d), (4)

Вместе с этим смотрят:

1C: Бухгалтерия

РЖнвентаризацiя активiв

Автоматизацiя бухгалтерського облiку ТОВ "Хлiбороб"

Автоматизацiя облiку зносу (амортизацii) необоротних активiв

Автоматизация бухгалтерского учета в современных условиях