Нормы и интерпретация результатов теста
Глава XIV
ПРОСТЕЙШИЕ МЕТОДЫ
СТАТИСТИЧЕСКОЙ ОБРАБОТКИ МАТЕРИАЛОВ ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
Статистические методы применяются при обработке материалов психологических исследований для того, чтобы извлечь из тех коВнличественных данных, которые получены в экспериментах, при опВнросе и наблюдениях, возможно больше полезной информации. В чаВнстности, в обработке данных, получаемых при испытаниях по псиВнхологической диагностике, это будет информация об индивидуальВнно-психологических особенностях испытуемых. Вообще психологиВнческие исследования обычно строятся с опорой на количественные данные. Вот пример.
К школьному психологу обратился шестиклассник Саня Ю. с просьВнбой испытать его двигательный темп. Саню очень интересовал басВнкетбол, и он собирался вступить в баскетбольную команду, а басВнкетболист, несомненно, должен иметь высокий двигательный темп. Психолог разработал план небольшого исследования. Он начал с того, что попросил Саню так быстро, как он только может, ставить точки в центре кружков, нарисованных на листке бумаги. За одну минуту Саня поставил 137 точек. Насколько этот темп характерен для Сани? Чтобы установить это, психолог попросил Саню повтоВнрить эту пробу 25 раз. Действительно, некоторые результаты преВнвышали первоначально полученное число, но некоторые оказались и поменьше. Психолог просуммировал все полученные за 25 проб реВнзультаты, а сумму разделил на 25 тАФ таким путем он получил средВннее арифметическое по всем пробам. Это среднее арифметическое составило 141. Таков по этой пробе максимальный темп Сани. Можно ли считать этот темп высоким? Потребовался еще один шаг в исследовании. Психолог сформировал группу из 50 шестиклассниВнков, не отличающихся ни от Сани, ни друг от друга по возрасту боВнлее чем на полгода. С этими ребятами психолог также провел снаВнчала по несколько тренировочных проб, чтобы получить надежные данные об их темпе, и, наконец, последнюю пробу, для обработки.
Все эти экспериментальные данные в виде средних арифметичеВнских были построены в один порядковый ряд, который был разбит по десяткам (по децилям). Санины данные вышли в десятку с наиВнболее быстрыми результатами. По этим количественным данным психолог сделал вывод о том, что Саня обладает сравнительно выВнсоким двигательным темпом, о чем и было ему сообщено.
Современная математическая статистика представляет собой большую и сложную систему знаний. Нельзя рассчитывать на то, что каждый психолог, сделавший диагностику своей специальноВнстью, овладеет этими знаниями. Между тем статистика нужна псиВнхологу постоянно в его повседневной работе. Специалисты-статисВнтики разработали целый комплекс простых методов, которые соВнвершенно доступны любому человеку, не забывшему то, что он выВнучил еще в средней школе.
В зависимости от требований, которые предъявляют к статистике различные области науки и практики, создаются пособия по геолоВнгической, медицинской, биологической, психологической статистиВнке. (См., например: Суходольский Г.В. Основы математической стаВнтистики для психологов. Л., 1972). В этой главе даются простейшие методы статистики для психологов. Все необходимые для их примеВннения вычисления можно выполнять на ручном компьютере, а то и на простых счетах. Уместное, грамотное применение этих методов позволит практику и исследователю, проведя начальную обработку, получить общую картину того, что дают количественные результаты его исследований, оперативно проконтролировать ход исследований. В дальнейшем, если возникнет такая необходимость, материалы исВнследований могут быть переданы для более глубокой разработки специалисту-статистику на большой компьютер.
Статистические шкалы. Применение тех или других статистиВнческих методов определяется тем, к какой статистической шкале относится полученный материал. С. Стивене предложил различать четыре статистические шкалы: шкалу наименований (или номинаВнтивную), шкалу порядка, шкалу интервалов и шкалу отношений.
Зная типические особенности каждой шкалы, нетрудно устаноВнвить, к какой из шкал следует отнести подлежащий статистической обработке материал.

 Шкала наименований. К этой шкале относятся материалы, в которых изучаемые объекты отличаются друг от друга по их качеВнству. При обработке таких материалов нет никакой нужды в том, чтобы располагать эти объекты в каком-то порядке, исходя из их характеристик. В принципе объекты можно располагать в любой последовательности. Вот пример: изучается состав международной научной конференции. Среди участников есть французы, англичане, датчане, немцы и русские (рис. 1). Имеет ли значение порядок, в котором будут расположены участники при изучении состава конВнференции? Можно распоВнложить их по алфавиту, это удобно, но ясно, что никаВнкого принципиального знаВнчения в этом расположении нет. При переводе этих маВнтериалов на другой язык (а значит, и на другой алфаВнвит) этот порядок будет нарушен. Можно располоВнжить национальные группы по числу участников. Но при сравнении этого материала с материалом другой конференции найдем, что вряд ли этот порядок окажется таким же. Отнесенные к шкале наВнименований объекты можно размещать в любой последовательности в зависимости от цели исследования.
Шкала наименований. К этой шкале относятся материалы, в которых изучаемые объекты отличаются друг от друга по их качеВнству. При обработке таких материалов нет никакой нужды в том, чтобы располагать эти объекты в каком-то порядке, исходя из их характеристик. В принципе объекты можно располагать в любой последовательности. Вот пример: изучается состав международной научной конференции. Среди участников есть французы, англичане, датчане, немцы и русские (рис. 1). Имеет ли значение порядок, в котором будут расположены участники при изучении состава конВнференции? Можно распоВнложить их по алфавиту, это удобно, но ясно, что никаВнкого принципиального знаВнчения в этом расположении нет. При переводе этих маВнтериалов на другой язык (а значит, и на другой алфаВнвит) этот порядок будет нарушен. Можно располоВнжить национальные группы по числу участников. Но при сравнении этого материала с материалом другой конференции найдем, что вряд ли этот порядок окажется таким же. Отнесенные к шкале наВнименований объекты можно размещать в любой последовательности в зависимости от цели исследования.
При статистической обработке такого рода материалов нужно считаться с тем, каким числом единиц представлен каждый объект. Имеются весьма эффективные статистические методы, позволяюВнщие по этим числовым данным прийти к научно значимым выводам (например, метод хи-квадрат).
Шкала порядка. Если в шкале наименований порядок следоваВнния изучаемых объектов практически не играет никакой роли, то в шкале порядка тАФ это видно из ее названия тАФ именно на эту поВнследовательность переключается все внимание. К этой шкале в стаВнтистике относят такие исследовательские материалы, в которых рассмотрению подлежат объекты, принадлежащие к одному или неВнскольким классам, но отличающиеся при сравнении одного с другим: большетАФменьше, вышетАФниже и т.п.
Проще всего показать типические особенности шкалы порядка, если обратиться к публикуемым итогам любых спортивных соревноВнваний. В этих итогах последовательно перечисляются участники, занявшие соответственно первое, второе, третье и прочие по порядВнку места. Но в информации об итогах соревнований нередко отсутВнствуют или отходят на второй план сведения о фактических достиВнжениях спортсменов, а на первый план ставятся их порядковые места. Допустим, шахматист Д. занял в соревнованиях первое меВнсто. Каковы же его достижения? Оказывается, он набрал 12 очков. Шахматист Е. занял второе место. Его достижение тАФ 10 очков.
Третье место занял Ж. с 8 очками, четвертое тАФ З. с 6 очками и т.д. В сообщениях о соревновании разница в достижениях при размеВнщении шахматистов отходит на второй план, а на первом остаются их порядковые места. В том, что именно порядковому месту отвоВндится главное значение, есть свой смысл. В самом деле, в нашем примере 3. набрал 6, а Д. тАФ 12 очков. Это абсолютные их достиВнжения тАФ выигранные ими партии. Если попытаться истолковать эту разницу в достижениях чисто арифметически, то пришлось бы признать, что 3. играет вдвое хуже, чем Д. Но с этим нельзя соглаВнситься. Обстоятельства соревнований не всегда просты, как не всеВнгда просто и то, как провел их тот или другой участник. Поэтому, воздерживаясь от арифметической абсолютизации, ограничиваются тем, что устанавливают: шахматист 3. отстает от занявшего первое место Д. на три порядковых места.
Заметим, что в других соревнованиях расклад абсолютных досВнтижений может быть иным: занявший первое место может всего на пол-очка опережать ближайших участников. Важно, что он набрал наибольшее количество очков. Только от этого зависит его порядкоВнвое место.
Шкала интервалов. К ней относятся такие материалы, в которых дана количественная оценка изучаемого объекта в фиксированных едиВнницах. Вернемся к опытам, которые провел психолог с Саней. В опытах учитывалось, сколько точек может поставить, работая с максимально доступной ему скоростью, сам Саня и каждый из его сверстников. Оценочными единицами в опытах служило число точек. Подсчитав их, исследователь получил то абсолютное число точек, которое оказалось возможным поставить за отведенное время каждому участнику опытов. Главная трудность при отнесении материалов к шкале интервалов соВнстоит в том, что нужно располагать такой единицей, которая была бы при всех повторных измерениях тождественной самой себе, т.е. одинаВнковой и неизменной. В примере с шахматистами (шкала порядка) такой единицы вообще не существует.
В самом деле, учитывается число партий, выигранных каждым участником соревнований. Но ясно, что партии далеко не одинакоВнвы. Возможно, что участник соревнований, занявший четвертое меВнсто тАФ он выиграл шесть партий, тАФ выиграл труднейшую партию у самого лидера! Но в окончательных итогах как бы принимается, что все выигранные партии одинаковы. В действительности же этого нет. Поэтому при работе с подобными материалами уместно их оценивать в соответствии с требованиями шкалы порядка, а не шкалы интервалов. Материалы, соответствующие шкале интерваВнлов, должны иметь единицу измерения.
Шкала отношений. К этой шкале относятся материалы, в коВнторых учитываются не только число фиксированных единиц, как в шкале интервалов, но и отношения полученных суммарных итогов между собой. Чтобы работать с такими отношениями, нужно иметь некую абсолютную точку, от которой и ведется отсчет. При изучеВннии психологических объектов эта шкала практически неприменима.
О параметрических и непараметрических методах статиВнстики. Приступая к статистической обработке своих исследований, психолог должен решить, какие методы ему более подходят по осоВнбенностям его материала тАФ параметрические или непараметричеВнские. Различие между ними легко понять. Вспомним, что говориВнлось об измерении двигательной скорости шестиклассников. Как обработать эти данные? Нужно записать все произведенные измеВнрения тАФ в данном случае это будет число точек, поставленных каВнждым испытуемым, тАФ затем требуется вычислить для каждого исВнпытуемого среднее арифметическое по результатам опытов. Далее следует расположить все эти данные в их последовательности, наВнпример, начиная с наименьших к наибольшим. Для облегчения обоВнзримости этих данных их обычно объединяют в группы; в этом слуВнчае можно объединить по 5тАФ9 измерений в группе. Вообще же при таком объединении желательно, если общее число случаев не более ста, чтобы общее число групп было порядка двенадцати. ПолучиВнлась такая таблица (с. 249).
Далее нужно установить, сколько раз в опытах встретились чиВнсловые значения, соответствующие каждой группе. Сделав это, нужно для каждой группы записать ее численность. Полученные в такой таблице данные носят название распределения численностей. Рекомендуется представить это распределение в виде диаграммы тАФ полигона распределения. Контуры этого полигона помогут решить вопрос о статистических методах обработки. Нередко они напомиВннают контуры колокола, с наивысшей точкой в центре полигона и с симметричными ветвями, отходящими в ту и другую сторону. Такой контур соответствует кривой нормального распределения. Это поняВнтие было введено в математическую статистику К.Ф. Гауссом (1777тАФ1855), поэтому кривую именуют также кривой Гаусса. Он же дал математическое описание этой кривой. Для построения криВнвой Гаусса (или кривой нормального распределения) теоретически требуется очень большое количество случаев. Практически же приВнходится довольствоваться тем фактическим материалом, который накоплен в исследовании. Если данные, которыми располагает исВнследователь, при их внимательном рассмотрении или после переноВнса их на диаграмму, лишь в незначительной степени расходятся с кривой нормального распределения, то это дает право исследоватеВнлю применять в статистической обработке параметрические методы, исходные положения которых основываются на нормальной (О математически обоснованных способах определения того, можно ли считать данное распределение нормальным, см., например, в кн.: Урбах В.Ю. МатематичеВнская статистика для биологов и медиков. М., 1963. С. 66) кривой распределения Гаусса. Нормальное распределение называют параВнметрическим потому, что для построения и анализа кривой Гаусса достаточно иметь всего два параметра: среднее арифметическое, значение которого должно соответствовать высоте перпендикуляра, восстановленного в центре кривой, и так называемое среднее квад-ратическое, или стандартное, отклонение тАФ величины, характериВнзующей размах колебаний данной кривой; о способах вычисления той и другой величины будет далее рассказано.
Параметрические методы обладают для исследователя многими преимуществами, но нельзя забывать о том, что применение их правомерно только тогда, когда обрабатываемые данные показывают распределение, лишь несущественно отличающееся от гауссова.
При невозможности применить параметрические методы, надлежит обратиться к непараметрическим. Эти методы успешно разрабатыВнвались в последние 3тАФ4 десятилетия, и их разработка была вызваВнна прежде всего потребностями ряда наук; в частности, психологии. Они показали свою высокую эффективность. Вместе с тем они не требуют сложной вычислительной работы.
Современному психологу-исследователю нужно исходить из того, что Влсуществует большое количество данных либо вообще не подВндающихся анализу с помощью кривой нормального распределения, либо не удовлетворяющих основным предпосылкам, необходимым для ее использованияВ» (Рунион Р. Справочник по непараметричеВнской статистике. М., 1982. С. 11.).
Генеральная совокупность и выборка. Психологу постоянно придется иметь дело с этими двумя понятиями. Генеральная совоВнкупность, или просто совокупность, тАФ это множество, все элеменВнты которого обладают какими-то общими признаками. Так, все подВнростки-шестиклассники 12 лет (от 11,5 до 12,5) образуют совокупВнность. Дети того же возраста, но не обучающиеся в школе, или же обучающиеся, но не в шестых классах, не подлежат включению в эту совокупность.
В ходе конкретизации проблем своего исследования психологу неизбежно придется обозначить границы изучаемой им совокупноВнсти. Следует ли включать в изучаемую совокупность детей того же возраста, но обучающихся в колледжах, гимназиях, лицеях и других подобных учебных заведениях? В ответе на этот и на другие такие же вопросы может помочь статистика.
В подавляющем большинстве случаев исследователь не в состояВннии охватить в изучении всю совокупность. Приходится, хотя это и связано с некоторой утратой информации, взять для изучения лишь часть совокупности, ее и называют выборкой. Задача исследователя заключается в том, чтобы подобрать такую выборку, которая репреВнзентировала бы, представляла совокупность; другими словами, приВнзнаки элементов совокупности должны быть представлены в выборВнке. Составить такую выборку, в точности повторяющую все разноВнобразные сочетания признаков, которые имеются в элементах совоВнкупности, вряд ли возможно. Поэтому некоторые потери в инфорВнмации оказываются неизбежными. Важно, чтобы в выборке были сохранены существенные, с точки зрения данного исследования, признаки совокупности. Возможны случаи, и для их обнаружения есть статистические методы, когда задачи исследования требуют создания двух выборок одной совокупности; при этом нужно устаВнновить, не взяты ли выборки из разных совокупностей. Эти и друВнгие подобные казусы нужно иметь в виду психологу при обработке результатов выборочных исследований.
Следует рассмотреть типы задач, с которыми чаще всего имеет дело психолог. Соответственно приводятся и статистичеВнские методы, которые приложимы для обработки психологических материалов, направленных на решение этих задач.
Первый тип задач. Психологу нужно дать сжатую и достаточВнно информативную характеристику психологических особенностей какой-то выборки, например, школьников определенного класса. Чтобы подойти к решению этой задачи, необходимо располагать реВнзультатами диагностических испытаний; эти испытания, разумеется, следует заранее спланировать так, чтобы они давали информацию о тех особенностях группы, которые в этом конкретном случае интеВнресуют психолога. Это могут быть особенности умственного развиВнтия, психофизиологические особенности, данные об изменении раВнботоспособности и т.д.
Получив все экспериментальные результаты и материалы наблюВндений, следует подумать о том, как их подать пользователю в комВнпактном виде, чтобы при этом свести к минимуму потерю информаВнции. В перечне статистических методов, используемых при решении подобных задач, обычно находят свое место и параметрические и непараметрические методы, о возможностях применения тех и друВнгих, как было сказано выше, судят по полученному материалу. Об этих статистических методах и их использовании пойдет речь ниже.
Второй тип задач. Это, пожалуй, наиболее часто встречающиеВнся задачи в исследовательской и практической деятельности психолога: сравниваются между собой несколько выборок, чтобы установить, являются ли выборки независимыми или принадлежат одной и той же совокупности. Так, проведя эксперименты в восьмых классах двух разВнличных школ, психолог сравнивает эти выборки между собой.
К этому же типу относятся задачи с определением тесноты связи двух рядов показателей, полученных на одной и той же выборке; в такой обработке чаще всего применяют метод корреляций.
Третий тип задач тАФ это задачи, в которых обработке подлежат временные ряды, в них расположены показатели, меняющиеся во времени; их называют также динамическими рядами. В предшестВнвующих типах задач фактор времени не принимался во внимание и маВнтериал анализировался так, как будто он весь поступил в руки исслеВндователя в одно и то же время. Такое допущение можно оправдать тем, что за тот короткий период времени, который был затрачен на собираВнние материала, он не потерпел существенных изменений. Но психологу приходится работать и с таким материалом, в котором наибольший инВнтерес представляют как раз его изменения во времени. Допустим, псиВнхолог намерен изучить изменение работоспособности школьников в теВнчение учебной четверти. В этом случае информативными будут показаВнтели, по которым можно судить о динамике работоспособности. Берясь за такой материал, психолог должен понимать, что при анализе динаВнмических рядов нет смысла пользоваться средним арифметическим ряВнда, так как оно замаскирует нужную информацию о динамике.
В предыдущих главах упоминалось о лонгитюдинальном исследоВнвании, т.е. таком, в котором однообразный по содержанию психолоВнгический материал по одной выборке собирается в течение длиВнтельного времени. Показатели лонгитюда тАФ это также динамичеВнские ряды, и при их обработке следует пользоваться методами, предназначенными для таких рядов.
Четвертый тип задач тАФ задачи, возникающие перед психолоВнгом, занимающимся конструированием диагностических методик, проверкой и обработкой результатов их применения. Отчасти об этих задачах уже говорилось в других главах, но не уделялось вниВнмания специально статистике. Психологическая диагностика, в осоВнбенности тестология, имеет целый ряд канонических правил, приВнменение которых должно обеспечивать высокое качество информаВнции, получаемой посредством диагностических методик. Так, метоВндика должна быть надежной, гомогенной, валидной. По упрочивВншимся в тестологии правилам, все эти свойства проверяются статиВнстическими методами.
Здесь уместно высказать некоторые соображения о возможностях статистики в проведении психологического исследования.
Статистика как таковая не создает новой научной информации. Эта информация либо содержится, либо не содержится (к сожалеВннию, и так бывает) в полученных исследователем материалах. НаВнзначение статистики состоит в том, чтобы извлечь из этих материаВнлов больше полезной информации. Вместе с тем статистика показыВнвает, что эта информация не случайна и что добытые данные имеют определенную и значимую вероятность.
Статистические методы раскрывают связи между изучаемыми явлеВнниями. Однако необходимо твердо знать, что как бы ни была высока вероятность таких связей, они не дают права исследователю признать их причинно-следственными отношениями. Статистика, как о ней пиВншут известные английские ученые Д.Э. Юл и М.Дж. Кендэл (Теория статистики. М., 1960. С. 18тАФ19.), Влвынуждена принимать к аналиВнзу данные, подверженные влиянию множества причинВ». Статистика, например, утверждает, что существует значимая связь между двиВнгательной скоростью и игрой в теннис. Но отсюда еще не вытекает, будто двигательная скорость и есть причина успешной игры. НельВнзя, по крайней мере в некоторых случаях, исключить и того, что сама двигательная скорость явилась следствием успешной игры.
Чтобы подтвердить или отвергнуть существование причинно-следственных отношений, исследователю зачастую приходится проВндумывать целые серии экспериментов. Если они будут правильно построены и проведены, то статистика поможет извлечь из резульВнтатов этих экспериментов информацию, которая необходима исслеВндователю, чтобы либо обосновать и подтвердить свою гипотезу, лиВнбо признать ее недоказанной.
Вот что нужно знать при использовании статистики.
Итак, были перечислены типы задач, с которыми чаще всего встречаются психологи. Теперь перейдем к изложеВннию конкретных статистических методов, которые способВнствуют успешному решению перечисленных задач.
Первый тип задач. Статистические методы, примеры их приВнменения для принятия решения.
Допустим, школьному психологу нужно представить краткую инВнформацию о развитии психомоторных функций учащихся 6-х классов, в которых обучается 50 учеников. В процессе выполнения своей проВнграммы психолог провел диагностическое изучение двигательной скоВнрости, применив методику, которая была описана выше (С. 240).
Для реализации своей программы психологу надлежало получить количественные характеристики, свидетельствующие о состоянии изучаемой функции тАФ ее центральной тенденции, величины, покаВнзывающей размах- колебаний, в пределах которого находятся все данные отдельных учеников, и то, как распределяются эти данные.
Какими методами вести обработку тАФ параметрическими или непараВнметрическими? Визуальное ознакомление с полученными данными поВнказывает, что возможно применение параметрического метода, т.е. буВндут вычислены среднее арифметическое, выражающее центральную тенденцию, и среднее квадратическое отклонение, показывающее разВнмах и особенности варьирования экспериментальных результатов.
Нельзя ограничиться вычислением только среднего арифметичеВнского, так как оно не дает полных сведений об изучаемой выборке. Вот пример. В одном купе вагона поместилась бабушка 60 лет с чеВнтырьмя внуками: 4 лет, двое по 5 и 6 лет. Среднее арифметическое возраста всех пассажиров этого купе 80/5 = 16.
В другом, купе расположилась компания молодежи: двое 15-летних, 16-летний и двое 17-летних. Средний возраст пассажиров этого купе также равен 16. Таким образом, по средним арифметиВнческим пассажиры этих купе как бы и не различаются. Но если обВнратиться к особенностям варьирования, то сразу можно установить, что в одном купе возраст пассажиров варьирует в пределах 56 едиВнниц, а во втором тАФ в пределах 2.
Для вычисления среднего арифметического применяется формула:
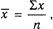
а для среднего квадратического отклонения формула:
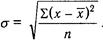
 В этих формулах х означает среднее арифметическое, х тАФ кажВндую величину изучаемого ряда, Z тАФ сумму; s тАФ среднее квадратиВнческое отклонение; п тАФ число членов изучаемого ряда.
В этих формулах х означает среднее арифметическое, х тАФ кажВндую величину изучаемого ряда, Z тАФ сумму; s тАФ среднее квадратиВнческое отклонение; п тАФ число членов изучаемого ряда.
Вернемся к опыту с проверкой двигательной скорости учащихся (С. 244).
В опытах участвовали 50 испытуемых. Каждый из них выполнил по 25 проб, по 1 минуте каждая. Вычислена средняя каждого испыВнтуемого. Полученный ряд упорядочен и все индивидуальные резульВнтаты представлены в последовательности от меньшего к большему:
85 тАФ 93 тАФ 93 тАФ 99 тАФ 101 тАФ 105 тАФ 109 тАФ 110 тАФ 111 тАФ 115 тАФ
115 тАФ 116 тАФ 116 тАФ 117 тАФ 117 тАФ 117 тАФ 118 тАФ 119 тАФ 121 тАФ 121 тАФ
122 тАФ 124 тАФ 124 тАФ 124 тАФ 124 тАФ 125 тАФ 125 тАФ 125 тАФ 127 тАФ 127 тАФ
127 тАФ 127 тАФ 127 тАФ 128 тАФ 130 тАФ 131 тАФ 132 тАФ 132 тАФ 133 тАФ 134 тАФ
134 тАФ 135 тАФ 138 тАФ 138 тАФ 140 тАФ 143 тАФ 144 тАФ 146 тАФ 150 тАФ 158
Для дальнейшей обработки удобнее эти первичные данные соВнединить в группы, тогда отчетливее выступает присущее данному ряду распределение величин и их численностей. Отчасти упрощается и вычисление среднего арифметического и среднего квадратического отклонения. Этим искупается несущественное искажение/ информации, неизбежное при вычислениях на сгруппированные данных.
При выборе группового интервала следует принять во внимание такие соображения. Если ряд не очень велик, например содержит до 100 элементов, то и число групп не должно быть очень велико, например порядка 10тАФ12. Желательно, чтобы при группировании начальная величина тАФ при соблюдении последовательности от меньшей величины к большей тАФ была меньше самой меньшей веВнличины ряда, а самая большая тАФ больше самой большой величины изучаемого ряда. Если ряд, как в данном случае, начинается с 85, группирование нужно начать с меньшей величины, а поскольку ряд заВнвершается числом 158, то и группирование должно завершаться большей величиной. В ряду, который нами изучается, с учетом высказанных соВнображений можно выбрать групповой интервал в 9 единиц и произвести разбиение ряда на группы, начав с 83. Тогда последняя группа будет заВнвершаться величиной, превышающей значение последней величины ряда (т.е. 158). Число групп будет равно 9 (табл. 1).
Вычисление среднего арифметического и среднего квадратическо-го отклонения.
Таблица 1
| Группы | Средние значеВнния | РезульВнтат разВнноски | Итоги разносВнки | fтАвx |  x тАУ x x тАУ x
|  (х -x)2 (х -x)2
|  fтАв(x -х)2 fтАв(x -х)2
|
| 83тАФ91 | 87 |  / /
| 1 | 87 | 36 | 1296 | 1296 |
| 92тАФ100 | 96 | u | 3 | 288 | 27 | 729 | 2187 |
| 101тАФ109 | 105 | LJ | 3 | 315 | 18 | 324 | 972 |
| 110тАФ118 | 114 | QQ | 10 | 1140 | 9 | 81 | 810 |
| 119тАФ127 | 123 | 1300/ | 16 | 1968 | 0 | 0 | 0 |
| 128тАФ136 | 132 | Ш | 9 | 1188 | 9 | 81 | 729 |
| 137тАФ145 | 141 | Я | 5 | 705 | 18 | 324 | 1620 |
| 146тАФ154 | 150 | L | 2 | 300 | 27 | 729 | 1458 |
| 155тАФ163 | 159 | / | 1 | 159 | 36 | 1296 | 1296 |
| | = 50 | | ΣfтАвx= 6150 | | |  ΣfтАв(x -х)2= =10368 ΣfтАв(x -х)2= =10368
|
1-й столбец тАФ группы, полученные после разбиения изучаемого ряда.
2-й столбец тАФ средние значения каждой группы; этот столбец показывает, в каком диапазоне варьируют величины изучаемого ряВнда, т.е. х.
3-й столбец показывает результаты ВлручнойВ» разноски величин ряда или иксов: каждая величина занесена в соответствующую ее значению группу в виде черточки.
4-й столбец тАФ это итог подсчета результатов разноски.
5-й столбец показывает, сколько раз встречалась каждая величиВнна ряда тАФ это произведение величин второго столбца на величины 4-го столбца по строчкам. Итоги 4-го и 5-го столбцов дают суммы, необходимые для вычисления среднего арифметического.
 6-й столбец показывает разность среднего арифметического и значения x по каждой группе.
6-й столбец показывает разность среднего арифметического и значения x по каждой группе.
7-й столбец тАФ квадрат этих разностей.
8-й столбец показывает, сколько раз встречался каждый квадрат разности; суммирование величин этого столбца дает итог, необхоВндимый для вычисления среднего квадратического отклонения.
В заголовках 5-го и 8-го столбцов указывается, насколько часто встречается та или другая величина. Частота обозначается буквой f (от английского слова frequency).
Включение буквы f, означающей, насколько часто встречалась та или другая величина, ничего не изменяет в формулах среднего арифметического и среднего квадратического отклонения.
Поэтому формулы
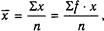
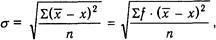
вполне тождественны.

Рис.2
Остается показать, как выВнчисляются по формулам средВннее арифметическое и среднее квадратическое отклонение. Обратимся к величинам, полуВнченным в таблице:
 x = 6150 : 50 = 123. При составлении таблицы это число было заранее вычислено, без него нельзя было бы полуВнчить числовые значения 6, 7, 8-го столбцов таблицы.
x = 6150 : 50 = 123. При составлении таблицы это число было заранее вычислено, без него нельзя было бы полуВнчить числовые значения 6, 7, 8-го столбцов таблицы.
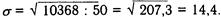
При обработке изучаемого ряда оказалось возможным применеВнние параметрического метода, так как визуально в этом ряду расВнпределение численностей приближается к нормальному. Это подВнтверждается и графиком (рис. 2, с. 251).



 Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах x В± s находится приВнмерно 68% всего ряда или всей выборки, в границах х В± 2s тАФ примерВнно 95%, а в границах x В± 3s тАФ 97,7% выборки. В практике исслеВндований часто берут границы тАФ x В±2/3s. В этих границах при норВнмальном распределении будут находиться 50% выборки; распредеВнление это симметрично, поэтому 25% окажутся ниже, а 25% выше границ x В±2/3s. Все эти расчеты не требуют никакой дополниВнтельной проверки при условии, что изучаемый ряд имеет норВнмальное распределение, а число элементов в нем велико, порядВнка нескольких сотен или тысяч. Для рядов, которые распределеВнны нормально или имеют распределение, мало отличающееся от нормального, вычисляется коэффициент вариации по такой форВнмуле:
Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах x В± s находится приВнмерно 68% всего ряда или всей выборки, в границах х В± 2s тАФ примерВнно 95%, а в границах x В± 3s тАФ 97,7% выборки. В практике исслеВндований часто берут границы тАФ x В±2/3s. В этих границах при норВнмальном распределении будут находиться 50% выборки; распредеВнление это симметрично, поэтому 25% окажутся ниже, а 25% выше границ x В±2/3s. Все эти расчеты не требуют никакой дополниВнтельной проверки при условии, что изучаемый ряд имеет норВнмальное распределение, а число элементов в нем велико, порядВнка нескольких сотен или тысяч. Для рядов, которые распределеВнны нормально или имеют распределение, мало отличающееся от нормального, вычисляется коэффициент вариации по такой форВнмуле:
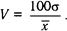
В примере, который был рассмотрен выше,
V= (100-14,4)/123 = 11,7.
Выполнив все эти вычисления, психолог может представить инфорВнмацию об изучении двигательной скорости с помощью примененной методики в 6-х классах. Согласно результатам изучения в 6-х классах получены: среднее арифметическое тАФ 123; среднее квадратическое отВнклонение тАФ 14,4; коэффициент вариативности тАФ 11,7.
Непараметрические методы. Ранжирование, медиана, квартиль. Далеко не все материалы, получаемые в психологичеВнских исследованиях, подлежат обработке параметрическими метоВндами. Если после ознакомления с изучаемым рядом исследователь убеждается в том, что этот ряд не имеет свойств нормального расВнпределения, ему остается перейти на методы непараметрической статистики. С их помощью могут быть получены и центральная тенденция изучаемого ряда тАФ медиана тАФ и величина, позволяющая судить о диапазоне варьирования и о строении изучаемого ряда тАФ квартильное отклонение.
Вот пример. После диагностических испытаний уровня умственВнного развития учеников 6-го класса полученные данные были упоВнрядочены, т.е. расположены в последовательности от меньшей веВнличины к большей. Испытания проходили 18 учащихся (табл. 2).
Таблица 2
| Учащиеся | Баллы | Ранги (R) | Учащиеся | Баллы | Ранги (R) |
| А | 25 | 1 | К | 68 | 10 |
| Б | 28 | 2 | Л | 69 | 11,5 |
| В | 39 | 4 | М | 69 | 11,5 |
| Г | 39 | 4 | Н | 70 | 14,5 |
| Д | 39 | 4 | О | 70 | 14,5 |
| Е | 45 | 6 | П | 70 | 14,5 |
| Ж | 50 | 7 | Р | 70 | 14,5 |
| 3 | 52 | 8,5 | С | 74 | 17,5 |
| И | 52 | 8,5 | Т | 74 | 17,5 |
Примечание. Буквами обозначены учащиеся, числами тАФ полученные ими баллы по тесту.
Процедура ранжирования состоит в следующем. Все числа ряда в их последовательности получают по своим. порядковым местам присваиВнваемые им ранги. Если какие-нибудь числа повторяются, то всем поВнвторяющимся числам присваивается один и тот же ранг тАФ средний из общей суммы занятых ими ранговых мест. Так, числу 28 в изучаемом ряду присвоен ранг 2. Затем следуют трижды повторяющиеся числа 39. На них приходятся занятые ими ранговые места 3, 4, 5. Поэтому этим числам присваивается один и тот же средний ранг, в данВнном случае тАФ 4. Поскольку места до 5-го включительно заняты, то следующее число получает ранг 6 и т.д.
При обработке ряда, не имеющего признаков нормального расВнпределения тАФ непараметрического ряда, тАФ для величины, которая выражала бы его центральную тенденцию, более всего пригодна меВндиана, т.е. величина, расположенная в середине ряда. Ее определяВнют по срединному рангу по формуле Me = (п + 1)/2, где Me тАФ озВнначает медиану, п тАФ как в ранее приводившихся формулах тАФ число членов ряда. При нечетном числе членов ряда ранговая медиана тАФ целое число, при нечетном число тАФ с 0,5. Заметим, что числовое значение медианы может и не быть в составе самого обрабатываеВнмого ряда.
Возьмем к примеру ряд в семь членов: 3тАФ5тАФ6тАФ7тАФ9тАФ10тАФ11.
Проранжировав его, имеем: 1тАФ2тАФ3тАФ4тАФ5тАФ6тАФ7.
Ранговая медиана в таком ряду равна: Me = (7 + 1)/2 = 4, этот ранг приходится на величину 7.
Возьмем ряд в восемь членов: 3тАФ5тАФ6тАФ7тАФ9тАФ10тАФ11тАФ12.
Проранжировав его, имеем: 1тАФ2тАФ3тАФ4тАФ5тАФ6тАФ7тАФ8.
Ранговая медиана в этом ряду равна: Me = (8 + 1)/2 = 4,5.
Этому рангу соответствует середина между двумя величинами, имеющими ранг 4 и ранг 5, т.е. между 7 и 9. Медиана этого ряда равна: Me = (7 + 9)/2 = 8.
Следует обратить внимание на то, что величины 8 в составе ряда нет, но таково значение медианы этого ряда.
Вернемся к изучаемому ряду. Он состоит из 18 членов. Его ранВнговая медиана равна: Me = (18 + 1)/2 = 9,5.
Она расположится между 9-й и 10-й величиной ряда. 9-я величиВнна тАФ 52, 10-я тАФ 68. Медиана занимает срединное место между ними, следовательно, Me = (52 + 68)/2 = 60.
По обе стороны от этой величины находится по 50% величин ряда.
Характеристику распределения численностей в непараметричеВнском ряду можно получить из отношения его квартилей. Квартилью называется величина, отграничивающая 1/4 всех величин ряда. Квартиль первая тАФ ее обозначение Q1 тАФ вычисляется по формуле:
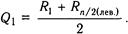
Это полусумма первого и последнего рангов первой тАФ левой от медианы половины ряда;
квартиль третья, обозначаемая Q3 вычисляется по формуле:
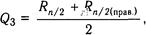
т.е. как полусумма первого и последнего рангов второй, правой от меВндианы, половины ряда. Берутся порядковые значения рангов по их поВнследовательности в ряду. В обрабатываемом ряду Q1 = (1+9)/2 = 5, Q3 = (10 + 18)/2 = 14.
Рангу 5 в этом ряду соответствует величина 39, а рангу 14 тАФ 70. Следовательно, в данном ряду Q1 = 39, а Q3= 70.
![]() Вместе с этим смотрят:
Вместе с этим смотрят:
Cистема роботи шкiльного психолога з профiлактики та подолання проблем статево-рольовоi поведiнки старшокласникiв
Features of evaluation and self-esteem of children of primary school age
Positive and negative values of conformism
РЖндивiдуально-психологiчнi особливостi здiбностей людини
А. Маслоу. Самоактуализирующиеся личности