бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме тАФ нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму.
На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571тАФ1630) в своих сочинениях тАЬНовая астрономиятАЭ.
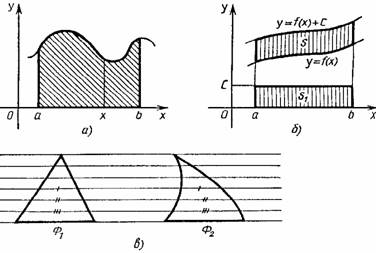
Рис 1.
(1609 г.) и ВлСтереометрия винных бочекВ» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры ограниченной эллипсом) и объемов (тело разрезалось на 6ecконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598тАФ1647) и Э.Торричелли (1608тАФ1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополнительных предположениях.
Пусть требуется найти площадь фигуры, изображенной на рисунке 1,б, где кривые, ограничивающие фигуру сверху и снизу, имеют уравнения y = f(x) и y=f(x)+c.
Представляя фигуру составленной из ВлнеделимыхВ», по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину с. Передвигая их в вертикальном направлении, можем составить из них прямоугольник с основанием bтАФа и высотой с. Поэтому искомая площадь равна площади полученного прямоугольника, т.е.
S = S1 = c ( b тАУ а ).
Общий принцип Кавальери для площадей плоских фигур формулируется так: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 1,в). Тогда площади фигур Ф1 и Ф2 равны.
Аналогичный принцип действует в стереометрии и оказывается полезны м при нахождении объемов.
В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П.Ферма уже в 1629 г. задачу квадратуры любой кривой у = хn, где п тАФ целое (т.е по существу вывел формулу ò хndx = (1/n+1)хn+1), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу (1630тАФ1677), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функций в виде степенных рядов.
Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия исчисления еще не было. Необходимо было выделить общие идеи лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известным под названием формулы Ньютона тАФ Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научится находить первообразные многих функций, дать логические нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М.В.Остроградский (1801тАФ1862), В.Я.Буняковский (1804тАФ1889), П.Л.Че бышев (1821тАФ1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции.
Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О.Коши, одного из крупнейших математиков, немецкого ученого Б.Римана (1826тАФ1866), французского математика Г.Дарбу (1842тАФ1917).
Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1838тАФ1922) теории меры.
Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875тАФ1941) и А. Данжуа (188 4тАФ1974), со ветским математиком А. Я. Х инчинчин ым (1894тАФ1959).
Определение и свойства интеграла
Если F(x) тАУ одна из первообразных функции f(x) на промежутке J, то первообразная на этом промежутке имеет вид F(x)+C, где CÎR.
Определение. Множество всех первообразных функции f(x) на промежутке J называется определенным интегралом от функции f(x) на этом промежутке и обозначается ò f(x)dx.
ò f(x)dx = F(x)+C, где F(x) тАУ некоторая первообразная на промежутке J.
f тАУ подынтегральная функция, f(x) тАУ подынтегральное выражение, x тАУ переменная интегрирования, C тАУ постоянная интегрирования.
Свойства неопределенного интеграла.
(ò f(x)dx) ¢ = ò f(x)dx ,
ò f(x)dx = F(x)+C, где F ¢(x) = f(x)
(ò f(x)dx) ¢= (F(x)+C) ¢= f(x)
ò f ¢(x)dx = f(x)+C тАУ из определения.
ò k f (x)dx = k ò f¢(x)dx
если k тАУ постоянная и F ¢(x)=f(x),
ò k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k ò f¢(x)dx
ò ( f(x)+g(x)+..+h(x) )dx = ò f(x)dx + ò g(x)dx +..+ ò h(x)dx
ò ( f(x)+g(x)+..+h(x) )dx = ò [F ¢(x)+G ¢(x)+..+H ¢(x)]dx =
= ò [F(x)+G(x)+..+H(x)] ¢dx = F(x)+G(x)+..+H(x)+C=
= ò f(x)dx + ò g(x)dx +..+ ò h(x)dx, где C=C1+C2+C3+..+Cn.
Интегрирование
Табличный способ.
Способ подстановки.
Если подынтегральная функция не является табличным интегралом, то возможно (не всегда) применить этот способ. Для этого надо:
разбить подынтегральную функцию на два множителя;
обозначить один из множителей новой переменной;
выразить второй множитель через новую переменную;
составить интеграл, найти его значение и выполнить обратную подстановку.
Примечание: за новую переменную лучше обозначить ту функцию, которая связана с оставшимся выражением.
Примеры:
1. ò xÖ(3x2тАУ1)dx;
Пусть 3x2тАУ1=t (t³0), возьмем производную от обеих частей:
6xdx = dt
xdx=dt/6
3
ó dt 1 1 ó 1 1 t 2 2 1 тАФтАФтАФØ
ôтАФ t 2 = тАФ ô t 2dt = тАУ тАФтАФтАУ + C = тАФÖ 3x2тАУ1 +C
õ 6 6 õ 6 3 9
2. t
ò sin x cos 3x dx = ò тАУ t3dt = тАУ тАУ + C
4
Пусть cos x = t
-sin x dx = dt
Метод преобразования подынтегральной функции в сумму или разность:
Примеры :
ò sin 3x cos x dx = 1/2 ò (sin 4x + sin 2x) dx = 1/8 cos 4x тАУ ¼ cos 2x + C
ó x4+3x2+1 ó 1 1
ôтАФтАФтАФтАФ dx = ô( x2+2 тАУ тАФтАФтАУ ) dx = тАФ x2 + 2x тАУ arctg x + C
õ x2+1 õ x2+1 3
Примечание: при решении этого примера хорошо делать многочлены тАЭугломтАЭ.
По частям
Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу.
(u(x)v(x))тАЩ=uтАЩ(x)v(x)+u(x)v(x)
uтАЩ(x)v(x)=(u(x)v(x)+u(x)vтАЩ(x)
Проинтегрируем обе части
ò uтАЩ(x)v(x)dx=ò (u(x)v(x))тАЩdx тАУ ò u(x)vтАЩ(x)dx
ò uтАЩ(x)v(x)dx=u(x)v(x)dx тАУ ò u(x)vтАЩ(x)dx
Примеры:
ò x cos (x) dx = ò x dsin x = x sin x тАУ ò sin x dx = x sin x + cos x + C
x = u(x)
cos x = vтАЩ(x)
Криволинейная трапеция
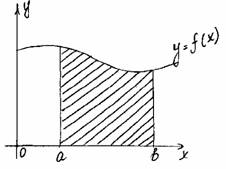
Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.
Способы нахождения площади криволинейной трапеции
Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных.
Дано: f(x)тАУ непрерывная неопр. функция, xÎ[a;b].
Доказать: S = F(b) тАУ F(a), где F(x) тАУ первообразная f(x).
Доказательство:

| 1) Рассмотрим вспомогательную функцию S(x). Каждому xÎ[a;b] поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой, проходящей через точку с этой абциссой и параллельно оси ординат. Следовательно S(a)=0 и S(b)=Sтр |
Докажем, что S(a) тАУ первообразная f(x).
D( f ) = D(S) = [a;b]
SтАЩ(x0)= lim( S(x0+Dx) тАУ S(x0) / Dx ), при DxВо0 DS тАУ прямоугольник
DxВо0 со сторонами Dx и f(x0)
SтАЩ(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) тАУ
DxВо0 DxВо0 первообразная f(x).
Следовательно по теореме об общем виде первообразной S(x)=F(x)+C.
Т.к. S(a)=0, то S(a) = F(a)+C
C = тАУFa
S = S(b)=F(b)+C = F(b)тАУF(a)
II.
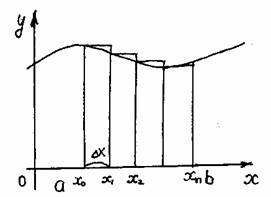
| 1). Разобьем отрезок [a;b] на n равных частей. Шаг разбиения Dx=(bтАУa)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+..+f(xn))Dx= nВо¥ = lim Dx(f(x0)+f(x1)+..+f(xn)) При nВо¥ получим, что Sтр= Dx(f(x0)+f(x1)+..+f(xn)) |
Предел этой суммы называют определенным интегралом.
Sтр=ò f(x)dx
a
Сумма стоящая под пределом, называется интегральной суммой.
Определенный интеграл это предел интегральной суммы на отрезке [a;b] при nВо¥. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала.
a тАФ нижний предел интегрирования;
b тАФ верхний.
Формула НьютонатАУЛейбница.
Сравнивая формулы площади криволинейной трапеции делаем вывод:
если F тАУ первообразная для b на [a;b], то
ò f(x)dx = F(b)тАУF(a)
a
ò f(x)dx = F(x) ô = F(b) тАУ F(a)
a a
Свойства определенного интеграла.
1.
ò f(x)dx = ò f(z)dz
a a
2.
a
ò f(x)dx = 0
a
a
ò f(x)dx = F(a) тАУ F(a) = 0
a
3.
b a
ò f(x)dx = тАУ ò f(x)dx
a b
b a
ò f(x)dx = F(a) тАУ F(b) ò f(x)dx = F(b) тАУ F(a) = тАУ (F(a) тАУ F(b))
a b
Если a, b и c любые точки промежутка I, на котором непрерывная функция f(x) имеет первообразную, то
b c b
ò f(x)dx = ò f(x)dx + ò f(x)dx
a a c
F(b) тАУ F(a) = F(c) тАУ F(a) + F(b) тАУ F(c) = F(b) тАУ F(a)
(это свойство аддитивности определенного интеграла)
Если l и m постоянные величины, то
ò (lf(x) +m j(x))dx = l ò f(x)dx + m òj(x))dx тАУ
a a c
тАУ это свойство линейности определенного интеграла.
6.
ò (f(x)+g(x)+..+h(x))dx = ò f(x)dx+ ò g(x)dx+..+ ò h(x)dx
a a a a
ò (f(x)+g(x)+..+h(x))dx = (F(b) + G(b) +..+ H(b)) тАУ
a
тАУ (F(a) + G(a) +..+ H(a)) +C =
= F(b)тАУF(a)+C1 +G(b)тАУG(a)+C2+..+H(b)тАУH(a)+Cn=
= ò f(x)dx+ ò g(x)dx+..+ ò h(x)dx
a a a
Набор стандартных картинок
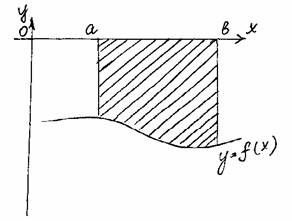
| Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)³0. Надо: рассмотреть симметрию функции относительно оси OX. ABCDВоAтАЩBтАЩCD b S(ABCD)=S(AтАЩBтАЩCD) = ò тАУf(x)dx a |
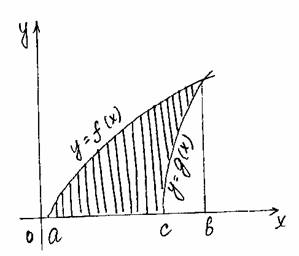
| b b S= ò f(x)dx = ò g(x)dx a a |
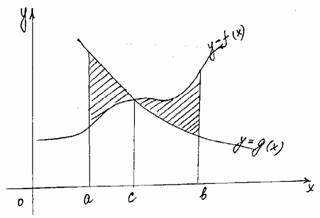
| c b S = ò (f(x)тАУg(x))dx+ò(g(x)тАУf(x))dx a c |
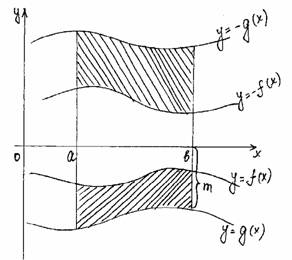
| f(x)Во f(x)+m g(x)Воg(x)+m S= ò (f(x)+mтАУg(x)тАУm)dx = a = ò (f(x)тАУ g(x))dx a Если на отрезке [a;b] f(x)³g(x), то площадь между этими графиками равна ò ((f(x)тАУg(x))dx a |
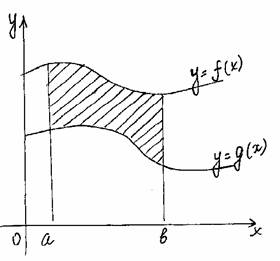
| Функции f(x) и g(x) произвольные и неотрицательные S=ò f(x)dx тАУ ò g(x)dx = ò (f(x)тАУg(x))dx a a a |
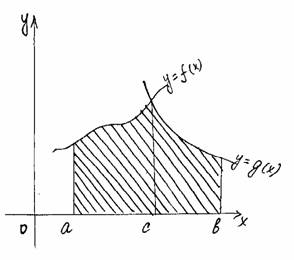
| b b S=ò f(x)dx + ò g(x)dx a a |
Применение интеграла
I. В физике.
Работа силы (A=FScosa, cosa ¹ 1)
Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно
d(mu2/2) = Fds
приращение кинетической энергии частицы за время dt равно скалярному произведению Fds, где ds тАУ перемещение частицы за время dt. Величина
dA=Fds
называется работой, совершаемой силой F.
Пусть точка движется по оси ОХ под действием силы, проекция которой на ось ОХ есть функция f(x) (fтАУнепрерывная функция). Под действием силы точка переместилась из точки S1(a) в S2(b). Разобьем отрезок [a;b] на n отрезков, одинаковой длины Dx = (b тАУ a)/n. Работа силы будет равна сумме работ силы на полученных отрезках. Т.к. f(x) тАУнепрерывна, то при малом [a;x1] работа силы на этом отрезке равна f(a)(x1тАУa). Аналогично на втором отрезке f(x1)(x2тАУx1), на n-ом отрезке тАФ f(xnтАУ1)(bтАУxnтАУ1). Следовательно работа на [a;b] равна:
А В» An = f(a)Dx +f(x1)Dx+..+f(xnтАУ1)Dx=
= ((bтАУa)/n)(f(a)+f(x1)+..+f(xnтАУ1))
Приблизительное равенство переходит в точное при nВо¥
А = lim [(bтАУa)/n] ( f(a)+..+f(xnтАУ1))= ò f(x)dx (по определению)
nВо¥ a
Пример.
Пусть пружина жесткости С и длины l сжата на половину свой длины. Определить величину потенциальной энергии Ер равна работе A, совершаемой силой тАУF(s) упругость пружины при её сжатии, то
l/2
Eп = A= тАУ ò (тАУF(s)) dx
0
Из курса механики известно, что F(s)= тАУCs.
Отсюда находим
l/2 l/2
Еп= тАУ ò (тАУCs)ds = CS2/2 | = C/2 l2/4
0 0
Ответ: Cl2/8.
Координаты центра масс
Центр масс тАУ точка через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.
Пусть материальная однородная пластина о имеет форму криволинейной трапеции {x;y |a£x£b; 0£y£f(x)} и функция y=f(x) непрерывна на [a;b], а площадь этойкриволинейной трапеции равна S, тогда координаты центра масс пластины о находят по формулам:
x0 = (1/S) ò x f(x) dx; y0 = (1/2S) ò f 2(x) dx;
a a
Примеры.
Центр масс.
Найти центр масс однородного полукруга радиуса R.
Изобразим полукруг в системе координат OXY.
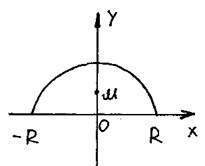
| Из соображений симметрии и однородности замечаем, что абсцисса точки M xm=0 Функция, описывающая полукруг имеет вид: y = Ö(R2тАУx2) Пусть S = pR2/2 тАФ площадь полукруга, тогда |
R R
y = (1/2S) òÖ(R2тАУx2)dx = (1/pR2) òÖ(R2тАУx2)dx =
тАУR тАУR
R
= (1/pR2)(R2xтАУx3/3)|= 4R/3p
тАУR
Ответ: M(0; 4R/3p )
Путь, пройденный материальной точкой
Если материальная точка движется прямолинейно со скоростью u=u(t) и за время T= t2тАУt1 (t2>t1) прошла путь S, то
t2
S=ò u(t)dt.
t1
В геометрии
Объём тАФ количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1ди, 1м и т.д.).
Количество кубов единичного объёма размещенных в данном теле тАФ объём тела.
Аксиомы объёма:
Объём тАФ это неотрицательная величина.
Объём тела равен сумме объёмов тел, его составляющих.
Найдем формулу для вычисления объёма:
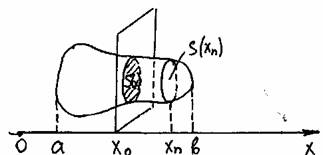
выберем ось ОХ по направлению расположения этого тела;
определим границы расположения тела относительно ОХ;
введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка [a;b] поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ.
разобьем отрезок [a;b] на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме
V=V1+V2+..+Vn=lim(S(x1)Dx +S(x2)Dx+..+S(xn)Dx
nВо¥
DxВо0, а SkВоSk+1, а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH.
Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при nВо¥ называется интегралом a
ò S(x)dx
a
V= ò S(x)dx, где S(x) тАУ сечение плоскости, проходящей через
b выбранную точку перпендикулярно оси ОХ.
Для нахождения объема надо:
1). Выбрать удобным способом ось ОХ.
2). Определить границы расположения этого тела относительно оси.
3). Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку.
4). Выразить через известные величины функцию, выражающую площадь данного сечения.
5). Составить интеграл.
6). Вычислив интеграл, найти объем.
Объем фигур вращения
Тело, полученное в результате вращения плоской фигуры, относительно какой-то оси, называют фигурой вращения.
Функция S(x) у фигуры вращения есть круг.
Sсеч = pr2
Sсеч(x)=p f 2(x)
V= ò f 2(x)
a
Длина дуги плоской кривой
Пусть на отрезке [a;b] функция y = f(x) имеет непрерывную производную yтАЩ = f тАЩ(x). В этом случае длину дуги l тАЬкускатАЭ графика функции y = f(x), xÎ[a;b] можно найти по формуле
l = ò Ö(1+fтАЩ(x)2)dx
a
Список литературы
М.Я.Виленкин, О.С.ИвашевтАУМусатов, С.И.Шварцбурд, тАЬАлгебра и математический анализтАЭ, Москва,1993г.
тАЬСборник задач по математическому анализутАЭ, Москва,1996г.
И.В.Савельев, тАЬКурс общей физикитАЭ, том 1, Москва, 1982г.
Вместе с этим смотрят:
"Инкарнация" кватернионов
*-Алгебры и их применение
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка