Проективная геометрия

Проективная геометрия развилась и выделилась в особую ветвь геометрических знаний в первые десятилетия 19 века. Источником этого явились потребности графики и архитектуры, развитие теории изображений в перспективе.

Так, французский геометр Понселе одним из первых выделил особые свойства геометрических фигур, названные им проективными.

Что это за свойства?

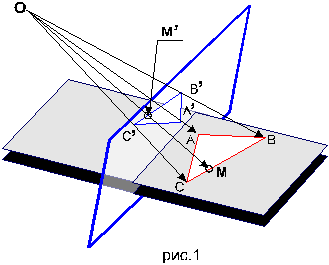
Пусть F- произвольная фигура в некоторой плоскости a , b - какая - либо другая плоскость, т.О - произвольная точка пространства, не принадлежащая ни одной плоскости (a и b). Точка, отсоединенная с любой точкой М фигуры F, определяет прямую (ОМ), пересекающую плоскость b в некоторой точке М/, которую мы будем называть проекцией точки М (на плоскости b из центра О).

Проекции всех точек фигуры F на плоскость b составят некоторую фигуру F/, которая называется проекцией фигуры F. Операция, с помощью которой в данной задаче из фигуры F получена фигура F/ носит название центрального проектирования из точки О. Если изменить положение точки О и плоскости b мы получим бесконечное множество фигур(или иначе говоря, центральных проекций фигуры F), которые в чем-то будут похожи на фигуру F, но в чем-то и отличаться. Например, проектируя правильный треугольник, получим тоже треугольник, но произвольной формы. Проектируя окружность, можем получить эллипс или параболу, или даже гиперболу. При таком проектировании не сохраняются метрические характеристики фигур (длина, площадь и т. д. ).

Какие же свойства сохраняются? Они обычно называются инвариантами преобразования, каковым в данном случае является преобразование проектирования. Именно эти свойства фигур, инвариантные по отношению к такому проектированию, Понселе назвал проективными свойствами, а предмет, их изучающий- проективной геометрией.

Примеры инвариантных свойств. Если фигура или объект - прямая, то после проектирования получим также прямую. Если фигура F- коническое сечение, т.е. описывается квадратичной формой a11x2+a22y2+a12xy+a13x+a23y+a33 =0, то проекцией точек на коническом сечении лягут также на некоторое коническое сечение. Таким образом, отдельные виды конических сечений (окружности, эллипсы, параболы, гиперболы) в проективной геометрии не отличаются - в отличие от аффинной, например, где эллипс всегда перейдет в эллипс.

Важной предпосылкой превращения проективной геометрии в самостоятельную дисциплину, было введение в употребление бесконечно удаленных геометрических элементов. Займемся их определением.

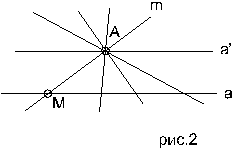
Пусть А - произвольная точка пространства и a - прямая, не проходящая через точку А. Проведем плоскость a через точку А и прямую а. Рассмотрим всевозможные прямые, проходящие через точку А и лежащие в плоскости a (рис.2).

Установим соответствие между прямыми пучка, проходящего через А и точками на прямой а. Например, лучу m соответствует точка M. Очевидно, что какую бы точку на прямой a мы ни выбрали, ей всегда соответствует определенный луч. Однако, нельзя утверждать, что любому лучу соответствует точка прямой a. Действительно, возьмем луч a/ , соответствующей точки на a мы не найдем. Таким образом, соответствие между лучами пучка и точками прямой a не является взаимно однозначными. Это не всегда удобно при операциях проектирования. Чтобы устранить это неудобно, условимся считать параллельные прямые, пересекающими на бесконечности. Тогда луч а/ из пучка А, параллельный а, будет иметь на этой прямой соответствующую точку ,но не обычную ,а называемую бесконечно удаленной точкой. Это новый геометрический объект. Все параллельные друг другу прямые в плоскости a имеют одну общую бесконечно удаленную точку, поэтому систему параллельных прямых называют пучком с бесконечно удаленным центром (рис.3).

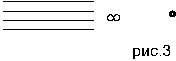
Бесконечно удаленные точки непараллельных прямых в плоскости считаются различными. Таким образом, каждая плоскость содержит бесконечно много различных бесконечно удаленных точек. Совокупность всех бесконечно удаленных точек плоскости называется бесконечно удаленной прямой.

Таким образом, каждая плоскость содержит одну бесконечно удаленную прямую.

Вполне логично совокупность всех бесконечно удаленных прямых назвать бесконечно удаленной плоскостью.

Выводы:

множество объектов обычного евклидова пространства дополняется новыми элементами:

К множеству точек каждой прямой добавляется одна бесконечно удаленная точка; К множеству прямых каждой плоскости добавляется одна бесконечно удаленная прямая; К множеству всех плоскостей пространства R3 добавляется бесконечно удаленная плоскость.

Определение: прямая дополненная бесконечно удаленной точкой называется проективной прямой.

Проективную прямую следует представлять в виде замкнутой линии. Плоскость, дополненная бесконечно удаленной прямой называется проективной плоскостью. Пространство, дополненное бесконечно удаленной плоскостью называется проективным пространством.

Термин бесконечности иногда употребляется и в обычной, элементарной геометрии (например, что параллельные прямые сходятся в бесконечности),но это лишь словесное выражение, в проективной же геометрии бесконечно удаленные элементы играют такую же роль, как и обыкновенные геометрические образы. В обычной геометрии большую роль играет изучение метрических свойств фигур (длины, площади, углы, объемы).

В проективной, процесс измерения теряет смысл, т. к например, один конец отрезка может оказаться в бесконечности. Таким образом, метрические свойства фигур не являются проективными свойствами.

Проективная геометрия, как и любая другая, строится на некоторой системе аксиом. Все аксиомы разбиты на три группы:

1.Аксиомы связи:

Кратко сформулируем их, учтя, что теперь в понятие любого объекта включается бесконечно удаленные элементы.

Какие бы ни были две точки А и В всегда существует прямая, проходящая через них. Какие бы ни были две различные точки А и В, существует не более одной прямой, проходящей через них. На каждой прямой имеется не менее трех точек. Существует по крайней мере 3 точки, не лежащие на одной прямой. Через каждые три точки А, B, C не лежащие на одной прямой, проходит некоторая плоскость a . На каждой плоскости имеется не менее одной точки. Через каждые три точки А, B, C не лежащие на одной прямой, проходит не более одной плоскости. Если две точки А и В прямой а лежат в плоскости a , то каждая точка прямой а лежит в плоскости a . Если две плоскости a и b имеют общую точку А, то они имеют еще по крайней мере одну общую точку. Имеется не менее четырех точек, не лежащих на одной плоскости. Каждые две прямые, расположенные в одной плоскости имеют общую точку.

Эти аксиомы повторяют аксиомы обычной евклидовой геометрии за исключением пункта 1.9, которого там нет.

2.Аксиомы порядка:

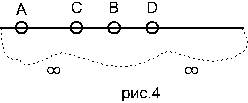
В элементарной геометрии в основу определения порядка следования точек на прямой заложено понятие о расположении точки между двумя другими точками. Т. е. если есть две точки А и В то обязательно найдется точка С на прямой А В, лежащая между А и В.

Такой порядок расположения точек является основой введения координат точек на прямой (в дальнейшем на плоскости и в пространстве), т.е. позволяет сделать отображение взаимного расположения точек на множество действительных чисел, ввести единицу измерения.

В проективной геометрии прямая есть замкнутая в бесконечности линия, поэтому нельзя в определение порядка положить принцип: что при заданных А и В найдется точка С между ними, определяющая порядок следования точек на прямой как А, В, C. И все-таки, какое-то определение порядка точек на проективной прямой необходимо сделать хотя бы для введения ней системы координат, определения проекции фигур в вычислительной геометрии или машинной графике.

На прямой в обычной евклидовой геометрии положение точек можно было характеризовать одним числом, одной координатой, отсчитываемой в некотором масштабе от точки, принятой за ноль. Так как в проективной геометрии бесконечно удаленная точка является равноправной с любой другой точкой, то уже невозможно одним числом представить координату этой бесконечно удаленной точки.

Здесь уже, на проективной прямой исходят из рассмотрения взаимного расположения двух пар точек.

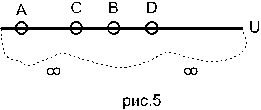
Пусть A и B, C и D две пары точек, расположенные на проективной прямой (рис.5). Тогда чтобы совместить точку C с другой точкой своей пары, т.е. CD мы при движении ее по прямой обязательно встретимся в какой-то момент с т. A или т. B. Аналогично, чтобы совместить B с A, при движении точки B она когда-нибудь совпадет с C или D. В таком случае говорят, что пара точек A и B разделяет пару точек C и D. На этом основаны аксиомы порядка и введения координат на проективной прямой.

Каковы бы ни были три различные точки A, B, C произвольной прямой U, на этой прямой существует такая точка D, что пара A, B разделяет пару C, D. Если пара A, B разделяет пару C, D; пара C, D разделяет пару A, B. Каковы бы ни были четыре различные точки A, B, C, D прямой из них могут быть всегда единственным образом составлены две раздельные пары.

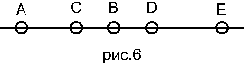
Аксиомы 2.4, 2.5 касаются взаимного расположения пяти точек. Если пары С,D и C, E разделяют A, B, то D E не разделяет A, В (рис.6). Если C, D и C, E не разделяют A, B, то D, E не разделяет A, B (рис.7).

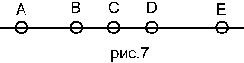
Пусть A, B и C, D две пары точек прямой U, A/, B/ и C/, D/ их проекции из какого угодно центра на произвольную другую прямую U/. Тогда если пары A, B и C, D разделяют друг друга, то пары A/, B/ и C/, D/ тоже разделяют друг друга.

Таким образом, разделенность двух пар точек есть свойство, инвариантное относительно проектирования. Это один из инвариантов проективной геометрии.

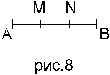
Это свойство позволяет упорядочивать точки на прямой. Так если дан отрезок АВ на проективной прямой, то множество его внутренних точек можно упорядочить так: точка M предшествует точке N, если пара A, N разделяет пару M, B (рис.8).

Две произвольные точки А, В проективной прямой U разделяют ее на два отрезка(рис.9). Чтобы отличить один из двух рассматриваемых отрезков от другого, нужно указать какую-нибудь его точку. Поэтому в проективной геометрии отрезок иногда обозначается тремя буквами. Например отрезок A С В обозначают отрезок с концами А, В и внутренней точкой С. Если точка D принадлежит другому отрезку то его можно обозначить А D В. Как легко видеть, пара точек А, В разделяет пару точек С, D. Отрезки А C В и A D B называются дополнительными друг к другу.

Мы рассмотрели, как вести порядок точек на каком-либо отрезке проективной прямой. Точки М, N , принадлежащие отрезку А В упорядочены так, что точка М предшествует точки N, если пара А, N разделяет пару M, B.

Чтобы это распространить на все точки отрезка А, В надо показать выполнение условия транзитивности: т.е. если точка М предшествует точке N, точка N предшествует точка Р, то точка М предшествует точке Р, т. е. надо показать, что пара АР разделяет пару M, B. Т. к. А, N разделяет пару М, В, то точка М лежит на отрезка А M N.

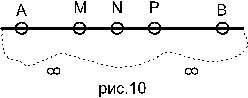
Т. к. A, P разделяет N, B, то точка N лежит на отрезке A N P, таким образом весь отрезок A M N лежит внутри отрезка A N P и т. о. точка М предшествует Р(рис.10).

Для дальнейшего введения системы координат на проективной прямой нам понадобится понятие гармонически сопряжённых пар точек. Для их определения рассматривается проективные понятия трёхвершинника и четырёхвершинника. Условимся называть трёхвершинником совокупность трёх точек, не лежащих на одной прямой и трёх прямых, попарно соединяющих эти точки (рис. 12).

Точки A, B, C назовём вершинами, прямые a, b, c сторонами трёхвершинника. Рассмотрим второй трёхвершинник A/, B/, C/. Для доказательств многих теорем проективной геометрии используется теорема Дезарга (являющаяся основной теоремой проективной геометрии). Сформулируем её: "Если соответственные стороны трёх вершинников ABC и A/B/C/ (т. е. AB и A/B/, BC и B/C/, AC и A/C/) пересекаются в точках P, Q, R лежащих на одной прямой, то прямые, соединяющие соответственные вершины сходятся в одной точке (O)". Справедлива и обратная теорема Дезарга: "Если прямые, соединяющие соответственные вершины двух трёхвершинников ABC и A/B/C/ сходятся в одной точке, то соответственные стороны пересекаются в точках лежащих на одной прямой". Обычно прямую u ,где расположены точки пересечения соответствующих сторон, называют осью преспективы, а точку, в которой сходятся прямые, соединяющие соответствующие вершины называют центром перспективы. Тогда обе теоремы Дезарга сформулируются одним утверждением: "Если два трёхвершинника имеют ось перспективы, то они имеют и центр перспективы и обратно".

Определение: Плоская фигура, составленная четырьмя точками, из которых никакие три не лежат на одной прямой, и шестью прямыми, соединяющими попарно эти точки называется полным четырёхвершинником.

Указанные стороны называются вершинами, прямые- сторонами четырёхвершинника. Вершины - A, B, C, D. Стороны- a, b, c, d, s, t (рис. 13).

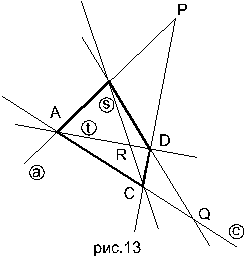
Стороны, не имеющие общей вершины, называются противоположными. Это a и d , b и c , s и t . Точки пересечения противоположных сторон называются диагональными точками четырёхвершинника. Здесь это точки P, Q, R. При помощи полного четырёхвершинника определяется понятие гармонически сопряжённых пар точек.

Определение: Пару точек S и T произвольной прямой и называют гармонически сопряжённой с парой точек P и Q этой же прямой, если P и Q суть диагональные точки некоторого четырёхвершинника, а точки S и T есть точки пересечения этой прямой с двумя противоположными сторонами четерёхвершинника, проходящими через третью диагональную точку.

Введённое определение позволяет построить четвёртую гармоническую точку к трём произвольно заданным точкам прямой u. Выберем вне прямой u некоторую т. B и на прямой PB некоторую т. A, отличную от P и от B. Тогда пересечение прямых AQ и BS определяет точку C. Пересечение прямых BQ и AC определяет точку D. Пересечение прямой AD с прямой u определяет четвертую гармоническую т. T. Т. О. положение т. T по трём заданным определяется однозначно.

Аналогично теореме Дезарга для двух трёхвершинников, существует подобная теорема для двух четырёхвершинников.

Теорема: Пусть ABCD и A/B/C/D/- два четырёхвершинника с двумя общими диагональными точками P и Q (пересечениями противоположных сторон AB и CD, A/B/ и C/D/ и AC и BD, A/C/ и B/D/ ).

Тогда, если стороны BC и B/C/ этих четырёхвершинников пересекаются в точке S прямой PQ, то их стороны AD и A/D/ пересекаются в точке T этой же прямой.

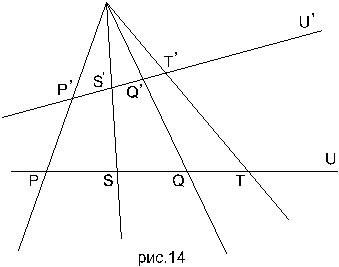
Если пара точек P и Q гармонически сопрежена с парой точек S и T, то и обратно пара точек S T гармонически сопряжена с P, Q.

Т. е. эти пары взаимно гармонические. Как и свойство взаимной раздельности пар, свойство гармонической сопряжённости инвариантно относительно проектирования (это инвариант проективной геометрии) (рис.14).

Т. e. если P, Q и S, T гармонически сопряжённые пары, то после проектирования из некоторого центра O на прямую и получим тоже гармонически сопряжённые пары P/, Q/ и S/, T/.

Важной также является теорема о том, что "Взаимно гармонические пары разделяют друг друга".

Теперь мы переходим к установлению принципа определения точек проективного пространства с помощью координат.

Построим сначала целочисленную систему координат на проективной прямой. Если эту прямую разрезать по её бесконечно удалённой точке, то множество конечных точек прямой можно упорядочить двумя различными способами(как бы по возрастанию и убыванию координат). Каждый из этих способов называется линейным порядком.

Возьмём на введённой проективной прямой a три точки из которых две помечены числами 0 и 1, а третья значком бесконечности. Точку бесконечности считаем бесконечно удалённой точкой прямой, точки 0 и 1- конечными, а прямую a- разрезанной в т. бесконечность.

Введём на прямой a линейный порядок так, чтобы т O предшествовала точке 1

Далее числом 2 пометим точку, которой вместе с точкой O составляет пару, гармонически

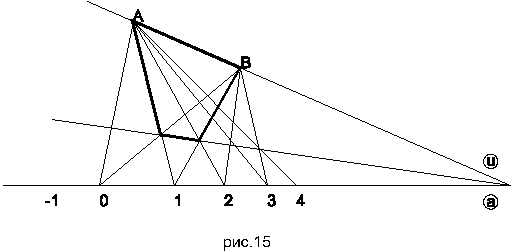
сопряженную с парой (1, бесконечность). По известной теореме такую точку можно всегда построить и к тому же пара (O, 2) разделяет пару (1, бесконечность). Поэтому в линейном порядке т. 1 лежит между т. O и т. 2, или иначе, т. 2 следует за т. O и т. 1.

Построить т. 2 можно так: проведём через т. бесконечность прямой a две прямые, пометим их числом 1 и буквой U. Выберем на прямой u любую точку A. Проведём прямые AO и A1.

Они в пересечении с прямой 1 дадут точки (1, 0) и (1, 1). Далее проведём через т. O и (1, 1) прямую до пересечения с прямой u получим т. B. Соединим B и 1 и найдём точку пересечения прямой B1 и 1. Это точка (1,2). Проектируя эту точку на прямую a из центра A получим т. 2. Она и будет той четвёртой точкой в гармонически сопряжённых парах O, 2 и 1, бесконечность. Это можно показать, рассмотрев четырёхвершинник A, B, (1, 1), (1, 2).

Далее процесс построения аналогичный. Проектируя точку 2 на прямую 1 из т. B получим точку (1, 3). Проектируя последнюю на прямую a из точки A получим т.4 и т. д.

Аналогично можно получить точки, помеченные отрицательными числами. Так мы выстроили шкалу для определения целочисленных координат точек на прямой. Далее мы начинаем дробить отрезки и находить сначала координаты типа Z= (X+ Y)/2.

Оказывается, что точки Z, бесконечность составляют гармоническую пару с X, Y. Сама точка Z называется проективным центром отрезка (X, Y). Дробя далее отрезки можно присвоить каждой следующей дробной точке определённое число.

Таким образом, разрезанной проективной прямой получает соответствующее число, которое называют проективной координатой.

На проективной плоскости каждая точка получает две проективные координаты, в проективном пространстве- три.

До сих пор мы устраивали координатную систему на разрезанной проективной прямой, при этом одна точка, обозначаемая бесконечность, никакой координаты не получала.

Чтобы все точки получили значения, приходится употреблять "Однородные координаты".

Рассмотрим вначале систему однородных координат на проективной прямой а.

Отметим, что любая точка М этой прямой имеет некоторую координату х, введенную так, как показано в предыдущей лекции при задании системы координат точками 0,1, ТР.При этом вполне определенную координату получает любая точка прямой, кроме точки ТР.

Введем для точки М два числа х1 и х2, не равные одновременно нулю и такие, что их отношение (х1/х2)равно х. Эти числа (х1,х2) будем называть однородными координатами точки М. С точкой ТР сопоставим однородные координаты х1, х2 при условии х2=0.

Свойства системы однородных координат: Каждая точка проективной прямой имеет однородные координаты. Если х1, х2 -однородные координаты т. М, то sх1, sх2, где s-любое число, отличное от нуля, есть тоже однородные координаты т. М. Разным точкам проективной прямой всегда соответствуют разные отношения их однородных координат.

Важнейшим свойством является второе: именно -каждая точка проективной прямой имеет бесконечно много пар однородных координат, которые сами по себе не определяются соответствующей им точкой, точка определяет лишь их отношение. Поэтому, подходящим подбором множителя s можно одну из координат взять равной единице (как правило -х2). Выпишем теперь однородные координаты базовых точек проективной прямой - точек 0, ТР,1, обозначаемых А1 , А2 , А3 . А1 (0,1), А2 (1,0), А3 (1,1).

Однородные координаты па проективной плоскости

На проективной плоскости все точки, кроме лежащих на прямой ТР (бесконечно удаленной прямой), имеют однородные проективные координаты. Базовыми точками для арифметизации проективной плоскости (т.е. введения проективных неоднородных координат) являются: начало системы координат О ; ТРХ (бесконечно удаленная на оси х), ТРy (бесконечно удаленная на оси y), (1,1) - единичная. Очевидно, бесконечно удаленная прямая проходит через точки ТРх и ТРy. Определим однородные проективные координаты сперва для точек проективной плоскости, не лежащих на прямой ТР. Однородными координатами такой точки М назовем три числа х1 , х2 , х3 , не равных одновременно нулю и таких, что х1/х2=х; х2/х3=y, где х и y - проективные неоднородные (обычные) координаты. Однородными координатами точки МТР , лежащей на прямой ТР , назовем три числа х1 , х2 , х3 при условиях:

х3=0; Из двух чисел х1 , х2 хотя бы одно отлично от нуля; Отношение х1/х2 равно В/ (-А), где А и В - коэффициенты любой прямой Ах+Ву+С=0, проходящей через точку МТР .

Если в уравнение прямой Ах+Ву+С=0 подставить однородные координаты некоторой точки М, лежащей на прямой (х=х1/х3, у=х2 /х3), то получим : Ах1+Вх2+Сх3=0, или иногда его записывают как:

u1 x1+u2 x2+u3 x3 = 0 - уравнение прямой в однородном виде (нет свободного члена)

Свойства однородных координат на плоскости:

1) Каждая точка проективной плоскости имеет однородные координаты

2) Если х1 , х2 , х3 - однородные координаты точки М, то s х1 , s х2 , s х3 (где s - любое отличное от нуля число) тоже являются однородными координатами точки М.

3) Разным точкам соответствуют разные отношения х1 / х3 , х2 / х3 их однородных координат.

Подходящим выбором s одну из координат можно сделать равной 1.Например, точка О - начало координат, получает однородные координаты (0,0,1), точка ТРх - (1, 0, 0), точка ТРу - (0,1,0), точка единиц по осям х и у - (1,1,1). Обозначим эти точки так: А1(1,0,0), А2(0,1,0), А3(0,0,1), Е(1,1,1) , их называют вершинами координатного триедра. Прямая А1 А2 - это бесконечно удаленная прямая - она имеет в однородных координатах уравнение х3 =0. Оси координат имеют свои обычные уравнения :

х1 =0, х2=0.

Однородные координаты в трехмерном пространстве.

Вводятся аналогично первым двум случаям. Сначала определим их для всех точек, не принадлежащих плоскости ТР (бесконечно удаленной плоскости).

Однородными координатами таких точек называются любые четыре числа х1 , х2 , х3 , х4 , не равные одновременно нулю, и такие, что х1 /х4=х , х2 /х4=у, х3 /х4=z, где х, у, z - М. Если же точка М принадлежит плоскости ТР , то ее однородные координаты определяются условиями : неоднородные (обычные) координаты точки:

х4=0; из трех чисел х1 , х2, х3 хотя бы одно отлично от нуля; отношение х1/х2/х3 равно отношению m/n/p, где m,n,p - параметры уравнения любой прямой, проходящей через точку МТР (х -х0 ) / m=(y -y0) ) / n=(z -z0 ) / p.

Аналогично уравнению прямой в однородном виде (u1 x1+u2 x2+u3 x3+u4 x4=0) можно записать уравнение плоскости в таком же виде: Ax+By+Cz+D=0 ,Ax1+Bx2+Cx3+Dx4=0 или u1x1+u2x2+u3x3+u4x4=0

Вершины координатного тетраэдра (пять точек): ТРx , ТРy , ТР z , 0, E

A1 (1,0,0,0) , A2 (0,1,0,0) , A3 (0,0,1,0) , A4 (0,0,0,1) , E (1,1,1,1) .

Аналитическое представление проективных преобразований (отображений)

1. Сначала рассмотрим проективные отображения плоскости на плоскость. Что такое проективное преобразование (отображение)? Очевидно, это такое отображение, при котором сохраняются проективные свойства объекта, например такое, как разделенность двух пар точек и гармонически сопряженные пары точек. Пусть М/=f(M) - проективное отображение (М - прообраз в исходной плоскости a, М/ - образ в преобразованной плоскости a/). Можно доказать, что и обратное отображение М=f-1 (M/) тоже является проективным, т.е. это взаимно однозначное отображение (биективное).Т.к. все проективные свойства опираются на свойства разделенности и гармонического сопряжения двух пар четырех соответствующих элементов (точек, прямых в пучке в одной плоскости), то существует теорема , по которой проективное отображение одной плоскости в другую однозначно определяется заданием четырех пар соответствующих по отображению точек, при условии, что никакие три из них не лежат на одной прямой. Показывается, что простейшим таким отображением является линейное отображение вида М(х1 ,х2 ,х3) Во М/ (s/x1/ , s/x2/ , s/x1/ )

s/x1/ =c11 x1+c12 x2+c13 x3 Числа сi k определяют матрицу такого преобразования,

(1) s/x2/ =c21 x1+c22 x2+c23 x3 причем для взаимной однозначности отображения

s/x3/ =c31 x1+c32 x2+c33 x3 необходимо, чтобы определитель матрицы № 0. По указанному выше замечанию преобразование (1) однозначно определено, если заданы четыре пары соответствующих точек М1 , М2 , М3 , М4 Во М/1 , M/2 , M/3 , M/4 . Более того, всякое линейное отображение вида (1) , определитель которого отличен от нуля, есть проективное отображение. Проективные преобразования составляют группу: это значит, что существует тождественное проективное преобразование (единичное) , обратное к заданному, а также произведение двух проективных преобразований есть снова проективное преобразование. Пусть заданы в плоскости a четыре точки Мk (k=1,2,3,4) с проективными координатами х1 k , х2 k , х3 k , никакие три из которых не лежат на одной прямой, и четыре точки М/k (k=1,2,3,4) в плоскости a/ с проективными координатами x/1 k , x/2 k , x/3 k , также никакие три из которых не лежат на одной прямой . Надо показать, что из линейных преобразований:

1)

s/kx/1 k =c11 x1 k+c12 x2 k+c13 x3 k

s/kx/2 k=c21 x1 k+c22 x2 k+c23 x3 k c №0

s/kx/3 k=c31 x1 k+c32 x2 k+c33 x3 k

можно однозначно найти 9 параметров сi k и 3 параметра s/k (k=1,2,3) , а s/4 всегда можно выбрать равным единице.

2) В трехмерном пространстве:

Каково бы ни было проективное отображение М/=f (M) точек пространства I на пространство I/ , проективные однородные координаты x/1 , x/2 , x/3 , x/4 точки М/ выражаются через проективные однородные координаты х1 , х2 , х3 , х4 точки М с помощью линейных соотношений:

s/kx/1 k=c11 x1 k+c12 x2 k+c13 x3 k+c14 x4 k

s/kx/2 k=c21 x1 k+c22 x2 k+c23 x3 k+c24 x4 k

(2) s/kx/3 k=c31 x1 k+c32 x2 k+c33 x3 k+c34 x4 k

s/kx/4 k=c41 x1 k+c42 x2 k+c43 x3 k+c44 x4 k

с постоянными коэффициентами сi k и при этом определитель матрицы такого преобразования D= с =(сi k) №0.

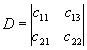3) Аналогичные определения существуют при проективном отображении прямой a на прямую a/. Если М/ - точка на прямой а/ с однородными координатами х/1 , x/2 ,и точка М - на прямой а с однородными координатами x1 , x2 ,то проективное преобразование М/ = f (M) однозначно определяется из соотношений:

s/x/1 = c11 x1+c12 x2

s/x/2= c21 x1+c22 x2 и

Часто бывает удобным использовать проективные преобразования в неоднородных координатах.

Для прямой : Если х1 , х2 - однородные координаты точки М на прямой ,то х=х1 / x2 - число, являющееся неоднородной координатой точки М на этой прямой . Пусть задано проективное преобразование прямой а на прямую а/ . Значит, существуют соотношения :

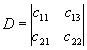
sx/1 = c11 x1+c12

sx/2 =c21 x1+c22 x2

Разделим почленно первое равенство на второе :

sx/1 /sx/2 =(c11 x1+c12 x2) / (c21 x1+c22 x2) , учитывая , что x/=x/1 / x/2 , и x=x1 / x2 .

Преобразуем

x/=(c11 x+c12)/ (c21 x+c22) , введя новые обозначения : a=c11 , b=c12 , g=c21 , d=c22

x/=(ax+b) / (gx+d) - т.е. в неоднородных координатах проективное преобразование выражается дробно - линейной функцией. ad -bg №0

Для плоскости : Однородные координаты точки М - х1 , х2 , х3 , неоднородные : x=x1 / x3 ,y=x2 / x3 .

Формулы проективного преобразования в неоднородных координатах :

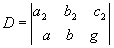x/=(a1 x+b1 y+c1) / (ax+by+ g) , a1 b1 c1 y/=(a2 x+b2 y+c2) / (ax+ by+ g) где

В трехмерном пространстве :

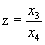
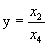
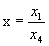
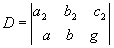Однородные координаты (x1 , x2 , x3 , x4)) .

Неоднородные координаты

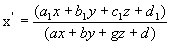
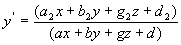
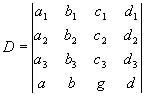
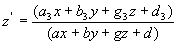
Рассмотрим подробнее проективные преобразования одномерных многообразий, здесь можно ограничится случаем преобразования прямой на прямую. Как установили ранее, в неоднородных проективных координат на прямой это преобразование имеет вид дробно-линейной функции (1) х/= a х+ b / g х+d , причем, чтобы существовало обратное проективное преобразование, необходимо, чтобы величина ad - bg № 0. Запишем преобразование (1) в виде функции х/= f(x).

Пусть данное отображение применяется последовательно два раза: х/= f(x), x//= f(x/)= f(f(x)). Тогда, если для любого элемента х одномерного многообразия (на прямой) выполняется соотношение x//= f(x/)= х (то есть дважды преобразованный возвращается в себя) , то такое проективное отображение называется инволюционным или инволюцией. Инволюция характеризуется еще и тем, что x= f(x/), т. е. обратное отображение х/= х совпадает с исходным х= х/. Найдем условие на коэффициенты в (1), при которых проективное отображение является инволюцией. Для этого из (1) выразим х через х/ : (g x /- a )x= - d x/ + b Ю x= - d x/+b / g x /- a (2). Из сравнения (1) и (2) видно, что отображения одинаковы тогда, когда либо:

а) d =- a , g, b - любые

б) d = a, g = b = 0 - но это тождественное отображение, которое исключим из рассмотрения.

Таким образом, из случая а) вытекает форма инволюционого проективного отображения х/= a х+ b /g х- в , где -a2- bg № 0 обозначим D = -a2- bg

Неподвижной точкой любого отображения называется точка, остающаяся неизменной после отображения. Для инволюции это означает , что х =х/= a х+ b /g х- в .

Решим последнее уравнение относительно х (3) g х2-2 a х- b= 0 - квадратное относительно х.

Это означает, что при инволюционном отображении число неподвижных точек не может быть больше 2.Дискреминант уравнения (3) есть a2+bg =-D.

Если -D<0, (дискриминант отрицательный), то уравнение (3) не имеет действительных корней, то есть нет ни одной неподвижной точки. Такая инволюция называется эллиптической (ее условие --a2-bg >0).

Если - D >0, то есть D<0 , -a2-bg <0 , то уравнение (3) имеет два действительных корня или две неподвижные точки- называется такая инволюция гиперболической.

Если D =0, то есть -a2-bg =0 , параболическая инволюция, но в этом случае такое отображение не входят в группу проективных преобразований, так как оно не взаимно однозначно.

Существует теорема , что для однозначного определения инволюции надо задать две пары соответствующих точек на прямой, в отличии от общих формул проективного отображения прямой на прямую, где надо задать три пары точек.

Следующий инвариант проективной геометрии - сложное отношение четырех точек на прямой.

Оно определяется так :Пусть М1,М2,M3,M4-четыре точки некоторой проективной прямой. Введем систему проективных неоднородных координат , и обозначим через t1,,t2,t3,t4, координаты заданных точек. Можно показать, что величина (t3-t1)/(t2-t3):(t4-t1)/(t2--t4 )

не зависит от выбора координатной системы, а определяется только положением точек на прямой.

Эта величина обозначается (М1 М2 M3 M4)= (t3-t1)/(t2-t3):(t4-t1)/(t2--t4 ) и называется сложным отношением четырех точек (СОЧТ).

Непосредственным вычислением можно показать, что выполняются два свойства СОЧТ.

1) (М1 М2 M3 M4)=(M3M4M1M2)

2) (М1 М2 M3 M4)= 1/ (М1 М2 M3 M4) то есть СОЧТ не меняется при перестановке первой и второй пар точек , изменяется на обратную величину при перестановке точек внутри какой-нибудь пары.

Важная теорема проективной геометрии гласит.

При любом проективном отображении прямой а на прямую а/ сложное отношение произвольной группы точек М1 М2 М3 М4 прямой а равно сложному отношению соответствующих им точек М1/ M2/ M3/ M4/ прямой а/ .

Частным ее случаем является утверждение:

В плоскости a заданы две прямые а и а/ ,задана произвольная точка S ,принадлежащая плоскости a ,но не лежащая на прямых а и а/. Тогда, сложное отношение любой четверки точек М1 М2 М3 М4 прямой а равно сложному отношению их проекций М1/М2/ М3/ М4/ из центра S на прямую а/ .

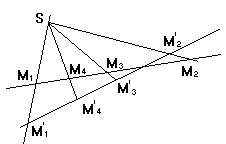
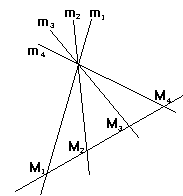
Аналогичное утверждение можносформулировать для плоского пучка из четырех лучей m1 m2 m3 m4

Любая прямая, пересекающаяэти четыре луча в

четырех точках, имеет для этих четырех точек одно и тоже сложное отношение.

(М1 М2 М3 М4)=инвариант проективной геометрии

или, что тоже самое (m1 m2 m3 m4 ) - инвариант проективной геометрии

Основной вывод : Сложное отношение четырех элементов одномерного многообразия - есть инвариант проективных отображений. Можно показать, что если пара точек А ,В гармонически разделяет пару точек С,D, то сочетание (А В С D)=-1.Оно вытекает из свойства гармонического сопряжения , когда каждая точка первой пары делит отрезок, образуемый второй парой точек внутренним и внешним образом в одинаковом отношении

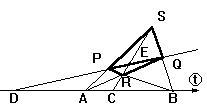
АС/AD=BC/BD или через неоднородные координаты ti точек (1,2,3,4) соответствует ( A , B , C , D )

(t3 - t1)/(t1 - t4) = (t2 - t3)/(t2 - t4) или (t3 - t1)/(t2 - t3) =

- (t4 - t1)/(t2 - t4) или ((t3 - t1)/(t2 - t3))/((t4 - t1)/(t2 - t4))=-1

Матрицы проективных преобразований.

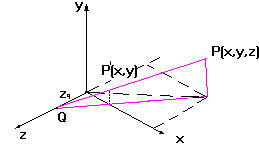
Представим перспективную проекцию объекта как проективное преобразование с центром проекции на оси z (на расстоянии zq от начала координат). Пусть плоскостью проекции является координатная плоскость XOY

P(x,y,z)-точка объекта , P/(X,Y)-её проекция из центра Q. Известно, что координаты точки-проекции P/ есть X=x/(1-z/zq) , Y=y/(1-z/zq) (*)

Однородные координаты точки P (x,y,z,1) - P/(x/,y /,z/,w /) ,w №0.

Преобразование (*) может быть выражено через матрицу проективных преобразований в однородных координатах:

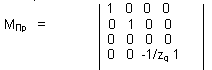
Неоднородные координаты точки P/

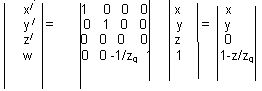
получаем отсюда : X=x/(1-z/zq ) ,

Y=y/(1-z/zq ) ,Z=0

Найдём проекцию бесконечно удаленной точки на оси Z - $ однородные координаты (0,0,1,0).

Вместо МПр возьмем матрицу полного проективного преобразования (без проецирования на плоскость XOY).

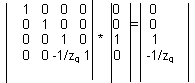
Неоднородные координаты проекции этой точки (0 ,0 , -zq )

Если взять семейство параллельных оси z прямых, то после такого проективного преобразования каждая из них пройдет через указанную точку (0,0,-zq ) на оси z .Поэтому эту точку называют точкой схода.

Аналогично, матрицы

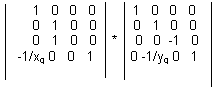
описывают проективные преобразования с точками схода на оси OX и OY. Это все преобразованные с одной точкой схода.

Матрица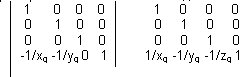

преобразование с двумя точками

А это с тремя схода

Групповые свойства проективных преобразований

Группа - есть совокупность объектов произвольной природы, которые называются элементами группы а обозначается символами a, b, c, .., удовлетворяющая требованиям следующих аксиом:

1. С каждой парой элементов совокупности, взятых в определённом порядке, сопоставлен по определённому закону некоторый третий элемент этой же совокупности.

Символически это записывают так c=ab, элемент c называется произведением (композицией) элементов a и b. Иначе: композиция двух любых элементов группы даёт элемент, принадлежащий этой же группе.

2. Закон ассоциативности: Каковы бы ни были три элемента группы a, b, c, всегда имеет место соотношение (ab)c=a(bc)

3. Существует такой элемент e , что для любого элемента a группы выполняется ae=a.

Элемент e называется единичным элементом.

4. Каким бы ни был элемент группы a, всегда существует такой элемент x, что ax=e.

Элемент x называется обратным элементу a и обозначается a-1, т. е. X= a-1.

Отсюда следуют такие правила:

a) если ax=e, то и xa=e

б) если e-единичный элемент группы, то ae= a и ea= a т. е. не различается "левая" и "правая" единицы

в) из соотношения ax= e обратный элемент x определяется однозначно

Если все эти положения применить к проективным преобразованиям, а именно к представляющим их матрицам проективных преобразований в однородных координатах, то можно сказать, что совокупность проективных преобразований составляет группу:

1) произведение двух проективных матриц есть вновь матрица проективного преобразования;

2) (c1c2)c3= c1(c2c3)

3) единичный элемент

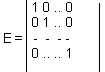
4) условием существования обратного элемента является условие существования обратной матрицы, для последнего не

Вместе с этим смотрят:

"Инкарнация" кватернионов

*-Алгебры и их применение

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнженерна графiка