Непрерывные генетические алгоритмы
Курсовая работа По дисциплине: ВлТеория систем и системный анализВ»
Выполнила тудентка 3 курса 1 группы Специальности ПИУ Антипина Г.С.
Государственный университет управления
Москва - 2006
Введение
В нашей жизни мы регулярно сталкиваемся с необходимостью решения оптимизационных и прогностических задач. Так, например, доход любой компании определяется качеством этих решений тАУ точностью прогнозов и оптимальностью выбранных стратегий.
Примерами таких задач могут являться:
Прогнозирование курсов валют;
Прогнозирование спроса;
Прогнозирование дохода компании;
Прогнозирование уровня безработицы;
Оптимизация расписаний;
Оптимизация плана закупок, плана инвестиций;
Оптимизация стратегии развития.
Как правило, для реальных задач бизнеса не существует четких алгоритмов решения. Раньше руководители и эксперты решали такие задачи только на основе личного опыта. С помощью аналитических технологий строятся системы, позволяющие существенно повысить эффективность решений.
Рассмотрим пример реальной задачи об оптимальном распределении инвестиций: Имеется инвестиционный капитал, который нужно распределить среди 10 проектов. Для каждого проекта задана функция зависимости прибыли от объема вложения. Требуется найти наиболее прибыльный вариант распределения капитала, при условии, что заданы минимальный и максимальный объем инвестиций для каждого проекта.
Традиционное решение: Чаще всего решение в данном случае принимает руководитель, основываясь только на личных впечатлениях о проектах. Размеры упущенной выгоды при этом не подсчитывают, и неоптимальность решения может остаться незамеченной.
Если же руководитель поручает аналитикам выбрать наиболее прибыльный вариант, применяются математические методы оптимизации. Если все данные функции линейны, то можно применить методы линейного программирования (симплекс-метод). Если хотя бы одна из функций нелинейна, то можно использовать метод градиентного спуска или полного перебора.
К сожалению, классические методики оказываются малоэффективными во многих практических задачах. Это связано с тем, что невозможно достаточно полно описать реальность с помощью небольшого числа параметров модели, либо расчет модели требует слишком много времени и вычислительных ресурсов.
В частности, рассмотрим проблемы, возникающие при решении этой задачи:
В реальной задаче ни одна из функций не известна точно - известны лишь приблизительные или ожидаемые значения прибыли. Для того, чтобы избавиться от неопределенности, мы вынуждены зафиксировать функции, теряя при этом в точности описания задачи.
Детерминированный алгоритм для поиска оптимального решения (симплекс-метод) применим только в том случае, если все данные функции линейны. В реальных задачах бизнеса это условие не выполняется. Хотя данные функции можно аппроксимировать линейными, решение в этом случае будет далеким от оптимального.
Если одна из функций нелинейна, то симплекс-метод неприменим, и остается два традиционных пути решения этой задачи:
Первый путь - использовать метод градиентного спуска для поиска максимума прибыли. В данном случае область определения функции прибыли имеет сложную форму, а сама функция - несколько локальных максимумов, поэтому градиентный метод может привести к неоптимальному решению.
Второй путь - провести полный перебор вариантов инвестирования. Если каждая из 10 функций задана в 100 точках, то придется проверить около 1020 вариантов, что потребует не менее нескольких месяцев работы современного компьютера.
Из-за описанных выше недостатков традиционных методик в последние 10 лет идет активное развитие аналитических систем нового типа. В их основе - технологии искусственного интеллекта, имитирующие природные процессы, такие как деятельность нейронов мозга или процесс естественного отбора.
Наиболее популярными и проверенными из этих технологий являются нейронные сети и генетические алгоритмы. Первые коммерческие реализации на их основе появились в 80-х годах и получили широкое распространение в развитых странах.
Теория алгоритмов. Задача коммивояжера.
В настоящее время теория алгоритмов развивается, главным образом, по трем направлениям.
Классическая теория алгоритмов изучает проблемы формулировки задач в терминах формальных языков, вводит понятие задачи разрешения, проводит классификацию задач по классам сложности P, NP и другим.
Теория асимптотического анализа алгоритмов рассматривает методы получения асимптотических оценок ресурсоемкости или времени выполнения алгоритмов, в частности, для рекурсивных алгоритмов. Асимптотический анализ позволяет оценить рост потребности алгоритма в ресурсах (например, времени выполнения) с увеличением объема входных данных.
Теория практического анализа вычислительных алгоритмов решает задачи получения явных функции трудоёмкости, интервального анализа функций, поиска практических критериев качества алгоритмов, разработки методики выбора рациональных алгоритмов.
В рамках классической теории осуществляется классификация задач по классам сложности (P-сложные, NP-сложные, экспоненциально сложные и др.).
К классу P относятся задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга).
К классу NP - задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, т.е. машины, следующее состояние которой не всегда однозначно определяется предыдущими. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу.
Другое определение класса NP: классом NP (от англ. non-deterministic polynomial) называют множество алгоритмов, время работы которых сильно зависит от размера входных данных, но если предоставить алгоритму некоторые дополнительные сведения (так называемых свидетелей решения), то он сможет достаточно быстро (за время, не превосходящее многочлена от размера данных) решить задачу. Проблема в том, что найти таких свидетелей бывает сложно, поэтому многие алгоритмы из класса NP считаются долгими. Классическим примером NP-задачи является задача коммивояжёра.
Задача коммивояжёра (коммивояжёр тАФ бродячий торговец) заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз, в таком случае выбор осуществляется среди гамильтоновых циклов[1] .
Существует масса разновидностей обобщённой постановки задачи, в частности геометрическая задача коммивояжёра (когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра.
Простейшие методы решения задачи коммивояжёра: полный лексический перебор, жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешёвого включения), метод минимального остовного дерева. На практике применяются различные модификации более эффективных методов: метод ветвей и границ и метод генетических алгоритмов.
Задача коммивояжёра есть NP-полная задача[2] . Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.
В основе метода ветвей и границ лежит простое наблюдение, что если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения. Это обычно выполняется с помощью глобальной переменной m, в которой запоминается минимальная верхняя граница, полученная для всех просмотренных до настоящего времени вариантах; любая вершина дерева поиска, нижняя граница которой больше m, может быть исключена из дальнейшего рассмотрения.
В следующем разделе мы перейдём к рассмотрению генетических алгоритмов.
Генетические алгоритмы. Общее описание. Математический аппарат.
Генетические алгоритмы предназначены для решения задач оптимизации. Примером подобной задачи может служить обучение нейросети, то есть подбора таких значений весов, при которых достигается минимальная ошибка. При этом в основе генетического алгоритма лежит метод случайного поиска. Основным недостатком случайного поиска является то, что нам неизвестно, сколько понадобится времени для решения задачи. Для того чтобы избежать таких расходов времени при решении задачи, применяются методы, проявившиеся в биологии. При этом используются методы открытые при изучении эволюции и происхождения видов. Как известно, в процессе эволюции выживают наиболее приспособленные особи. Это приводит к тому, что приспособленность популяции возрастает, позволяя ей лучше выживать в изменяющихся условиях.
Впервые подобный алгоритм был предложен в 1975 году Джоном Холландом (John Holland) в Мичиганском университете. Он получил название Влрепродуктивный план ХолландаВ» и лег в основу практически всех вариантов генетических алгоритмов. Однако, перед тем как мы его рассмотрим подробнее, необходимо остановится на том, каким образом объекты реального мира могут быть закодированы для использования в генетических алгоритмах.
Представление объектов.
Из биологии мы знаем, что любой организм может быть представлен своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе. Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. Все дальнейшее функционирование механизмов генетического алгоритма производится на уровне генотипа, позволяя обойтись без информации о внутренней структуре объекта, что и обуславливает его широкое применение в самых разных задачах.
В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются битовые строки. При этом каждому атрибуту объекта в фенотипе соответствует один ген в генотипе объекта. Ген представляет собой битовую строку, чаще всего фиксированной длины, которая представляет собой значение этого признака.
Кодирование признаков, представленных целыми числами
Для кодирования таких признаков можно использовать самый простой вариант тАУ битовое значение этого признака. Тогда нам будет весьма просто использовать ген определенной длины, достаточной для представления всех возможных значений такого признака. Но, к сожалению, такое кодирование не лишено недостатков. Основной недостаток заключается в том, что соседние числа отличаются в значениях нескольких битов, так например числа 7 и 8 в битовом представлении различаются в 4-х позициях, что затрудняет функционирование генетического алгоритма и увеличивает время, необходимое для его сходимости. Для того, чтобы избежать эту проблему лучше использовать кодирование, при котором соседние числа отличаются меньшим количеством позиций, в идеале значением одного бита. Таким кодом является код Грея, который целесообразно использовать в реализации генетического алгоритма. Значения кодов Грея рассмотрены в таблице ниже:
| Двоичное кодирование | Кодирование по коду Грея |
| Десятичный код | Двоичное значение | Шестнадцатеричное значение | Десятичный код | Двоичное значение | Шестнадцатеричное значение |
| 0 | 0000 | 0h | 0 | 0000 | 0h |
| 1 | 0001 | 1h | 1 | 0001 | 1h |
| 2 | 0010 | 2h | 3 | 0011 | 3h |
| 3 | 0011 | 3h | 2 | 0010 | 2h |
| 4 | 0100 | 4h | 6 | 0110 | 6h |
| 5 | 0101 | 5h | 7 | 0111 | 7h |
| 6 | 0110 | 6h | 5 | 0101 | 5h |
| 7 | 0111 | 7h | 4 | 0100 | 4h |
| 8 | 1000 | 8h | 12 | 1100 | Ch |
| 9 | 1001 | 9h | 13 | 1101 | Dh |
| 10 | 1010 | Ah | 15 | 1111 | Fh |
| 11 | 1011 | Bh | 14 | 1110 | Eh |
| 12 | 1100 | Ch | 10 | 1010 | Ah |
| 13 | 1101 | Dh | 11 | 1011 | Bh |
| 14 | 1110 | Eh | 9 | 1001 | 9h |
| 15 | 1111 | Fh | 8 | 1000 | 8h |
Таблица 1. Соответствие десятичных кодов и кодов Грея.
Таким образом, при кодировании целочисленного признака мы разбиваем его на тетрады и каждую тетраду преобразуем по коду Грея.
В практических реализациях генетических алгоритмов обычно не возникает необходимости преобразовывать значения признака в значение гена. На практике имеет место обратная задача, когда по значению гена необходимо определить значение соответствующего ему признака.
Таким образом, задача декодирования значения генов, которым соответствуют целочисленные признаки, тривиальна.
Кодирование признаков, которым соответствуют числа с плавающей точкой
Самый простой способ кодирования, который лежит на поверхности тАУ использовать битовое представление. Хотя такой вариант имеет те же недостатки, что и для целых чисел. Поэтому на практике обычно применяют следующую последовательность действий:
Разбивают весь интервал допустимых значений признака на участки с требуемой точностью.
Принимают значение гена как целочисленное число, определяющее номер интервала (используя код Грея).
В качестве значения параметра принимают число, являющиеся серединой этого интервала.
Рассмотрим вышеописанную последовательность действий на примере:
Допустим, что значения признака лежат в интервале [0,1]. При кодировании использовалось разбиение участка на 256 интервалов. Для кодирования их номера нам потребуется таким образом 8 бит. Допустим значение гена: 00100101bG (заглавная буква G показывает, что используется кодирование по коду Грея). Для начала, используя код Грея, найдем соответствующий ему номер интервала: 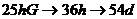 . Теперь посмотрим, какой интервал ему соответствуеттАж После несложных подсчетов получаем интервал
. Теперь посмотрим, какой интервал ему соответствуеттАж После несложных подсчетов получаем интервал 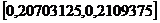 . Значит значение нашего параметра будет
. Значит значение нашего параметра будет 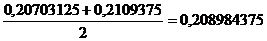 .
.
Основные генетические операторы
Как известно в теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). Этот оператор определяет передачу признаков родителей потомкам. Действует он следующим образом:
из популяции выбираются две особи, которые будут родителями;
определяется (обычно случайным образом) точка разрыва;
потомок определяется как конкатенация части первого и второго родителя.
Рассмотрим функционирование этого оператора:
| Хромосома_1: | 0000000000 |
| Хромосома_2: |
|
Допустим разрыв происходит после 3-го бита хромосомы, тогда
| Хромосома_1: | 0000000000 | >> | 000 | 1111111 | Результирующая_хромосома_1 |
| Хромосома_2: |
| >> | 111 | 0000000 | Результирующая_хромосома_2 |
Затем с вероятностью 0,5 определяется одна из результирующих хромосом в качестве потомка.
Следующий генетический оператор предназначен для того, чтобы поддерживать разнообразие особей с популяции. Он называется оператором мутации. При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется.
Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами. Схематически это можно представить следующим образом:
В принципе для функционирования генетического алгоритма достаточно этих двух генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации этих двух операторов. Например, кроссовер может быть не одноточечный (как было описано выше), а многоточечный, когда формируется несколько точек разрыва (чаще всего две). Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.
Схема функционирования генетического алгоритма
Теперь, зная как интерпретировать значения генов, перейдем к описанию функционирования генетического алгоритма. Рассмотрим схему функционирования генетического алгоритма в его классическом варианте.
Инициировать начальный момент времени 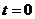 . Случайным образом сформировать начальную популяцию, состоящую из k особей.
. Случайным образом сформировать начальную популяцию, состоящую из k особей.
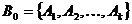
Вычислить приспособленность каждой особи 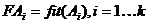 и популяции в целом
и популяции в целом 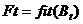 (также иногда называемую термином фиттнес). Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.
(также иногда называемую термином фиттнес). Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.
Выбрать особь 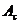 из популяции.
из популяции. 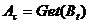
С определенной вероятностью (вероятностью кроссовера 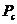 ) выбрать вторую особь из популяции
) выбрать вторую особь из популяции 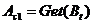 и произвести оператор кроссовера
и произвести оператор кроссовера 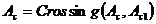 .
.
С определенной вероятностью (вероятностью мутации 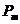 ) выполнить оператор мутации.
) выполнить оператор мутации. 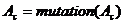 .
.
С определенной вероятностью (вероятностью инверсии 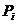 ) выполнить оператор инверсии
) выполнить оператор инверсии 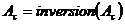 .
.
Поместить полученную хромосому в новую популяцию 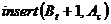 .
.
Выполнить операции, начиная с пункта 3, k раз.
Увеличить номер текущей эпохи 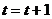 .
.
Если выполнилось условие останова, то завершить работу, иначе переход на шаг 2.
Теперь рассмотрим подробнее отдельные этапы алгоритма.
Наибольшую роль в успешном функционировании алгоритма играет этап отбора родительских хромосом на шагах 3 и 4. При этом возможны различные варианты. Наиболее часто используется метод отбора, называемый рулеткой. При использовании такого метода вероятность выбора хромосомы определяется ее приспособленностью, то есть 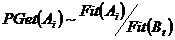 . Использование этого метода приводит к тому, что вероятность передачи признаков более приспособленными особями потомкам возрастает. Другой часто используемый метод тАУ турнирный отбор. Он заключается в том, что случайно выбирается несколько особей из популяции (обычно 2) и победителем выбирается особь с наибольшей приспособленностью. Кроме того, в некоторых реализациях алгоритма применяется так называемая стратегия элитизма, которая заключается в том, что особи с наибольшей приспособленностью гарантировано переходят в новую популяцию. Использование элитизма обычно позволяет ускорить сходимость генетического алгоритма. Недостаток использования стратегии элитизма в том, что повышается вероятность попадания алгоритма в локальный минимум.
. Использование этого метода приводит к тому, что вероятность передачи признаков более приспособленными особями потомкам возрастает. Другой часто используемый метод тАУ турнирный отбор. Он заключается в том, что случайно выбирается несколько особей из популяции (обычно 2) и победителем выбирается особь с наибольшей приспособленностью. Кроме того, в некоторых реализациях алгоритма применяется так называемая стратегия элитизма, которая заключается в том, что особи с наибольшей приспособленностью гарантировано переходят в новую популяцию. Использование элитизма обычно позволяет ускорить сходимость генетического алгоритма. Недостаток использования стратегии элитизма в том, что повышается вероятность попадания алгоритма в локальный минимум.
Другой важный момент тАУ определение критериев останова. Обычно в качестве них применяются или ограничение на максимальное число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра.
3. Непрерывные генетические алгоритмы.
Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены теоретические результаты о целесообразности использования именно двоичного алфавита. К тому же, реализация такого генетического алгоритма на ЭВМ была сравнительно легкой. Все же, небольшая группа исследователей шла по пути применения в генетических алгоритмах отличных от двоичных алфавитов для решения частных прикладных задач. Одной из таких задач является нахождение решений, представленных в форме вещественных чисел, что называется не иначе как Влпоисковая оптимизация в непрерывных пространствахВ». Возникла следующая идея: решение в хромосоме представлять напрямую в виде набора вещественных чисел. Естественно, что потребовались специальные реализации биологических операторов. Такой тип генетического алгоритма получил название непрерывного генетического алгоритма (RGA, или real-coded genetic algorithm), или генетического алгоритма с вещественным кодированием.
Первоначально непрерывные гены стали использоваться в специфических приложениях (например, хемометрика, оптимальный подбор параметров операторов стандартных генетических алгоритмов и др.). Позднее они начинают применяться для решения других задач оптимизации в непрерывных пространствах (работы исследователей Wright, Davis, Michalewicz, Eshelman, Herrera в 1991-1995 гг). Поскольку до 1991 теоретических обоснований работы непрерывных генетических алгоритмов не существовало, использование этого нового подвида было спорным; ученые, знакомые с фундаментальной теорией эволюционных вычислений, в которой было доказано превосходство двоичного алфавита перед другими, критически воспринимали успехи алгоритмов с вещественным кодированием. После того, как спустя некоторое время теоретическое обоснование появилось, непрерывные генетические алгоритмы полностью вытеснили двоичные хромосомы при поиске в непрерывных пространствах.
Преимущества и недостатки двоичного кодирования
Прежде чем излагать особенности математического аппарата непрерывных генетических алгоритмов, остановимся на анализе достоинств и недостатков двоичной схем кодирования.
Как известно, высокая эффективность отыскания глобального минимума или максимума генетическим алгоритмом с двоичным кодированием теоретически обоснована в фундаментальной теореме генетических алгоритмов (Влтеореме о шаблонеВ»), доказанной Холландом. Ее суть в том, что двоичный алфавит позволяет обрабатывать максимальное количество информации по сравнению с другими схемами кодирования.
Однако двоичное представление хромосом влечет за собой определенные трудности при поиске в непрерывных пространствах большой размерности, и когда требуется высокая точность найденного решения. В генетических алгоритмах с двоичным кодированием для преобразования генотипа в фенотип используется специальный прием, основанный на том, что весь интервал допустимых значений признака объекта 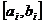 разбивается на участки с требуемой точностью. Заданная точность p определяется выражением
разбивается на участки с требуемой точностью. Заданная точность p определяется выражением
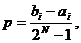
где N тАУ количество разрядов для кодирования битовой строки.
Эта формула показывает, что p сильно зависит от N, т.е. точность представления определяется количеством разрядов, используемых для кодирования одной хромосомы. Поэтому при увеличении N пространство поиска расширяется и становится огромным.
Известный книжный пример: пусть для 100 переменных, изменяющихся в интервале 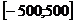 , требуется найти экстремум с точностью до шестого знака после запятой. В этом случае при использовании генетических алгоритмов с двоичным кодированием длина строки составит 3000 элементов, а пространство поиска тАУ около
, требуется найти экстремум с точностью до шестого знака после запятой. В этом случае при использовании генетических алгоритмов с двоичным кодированием длина строки составит 3000 элементов, а пространство поиска тАУ около 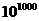 хромосом.
хромосом.
Эффективность генетических алгоритмов с двоичным кодированием в этом случае будет невысокой. На первых итерациях алгоритм потратит много усилий на оценку младших разрядов числа, закодированных во фрагменте двоичной хромосомы. Но оптимальное значение на первых итерациях будет зависеть от старших разрядов числа. Следовательно, пока в процессе эволюции алгоритм не выйдет на значение старшего разряда в окрестности оптимума, операции с младшими разрядами окажутся бесполезными. С другой стороны, когда это произойдет, станут не нужны операции со старшими разрядами тАУ необходимо улучшать точность решения поиском в младших разрядах. Такое ВлидеальноеВ» поведение не обеспечивает семейство генетических алгоритмов с двоичным кодированием, т.к. эти алгоритмы оперируют битовой строкой целиком, и на первых же эпохах младшие разряды чисел "застывают", принимая случайное значение. В классических генетических алгоритмах разработаны специальные приемы по выходу из этой ситуации. Например, последовательный запуск ансамбля генетических алгоритмов с постепенным сужением пространства поиска.
Есть и другая проблема: при увеличении длины битовой строки необходимо увеличивать и численность популяции.
Математический аппарат непрерывных генетических алгоритмов
Как уже отмечалось, при работе с оптимизационными задачами в непрерывных пространствах вполне естественно представлять гены напрямую вещественными числами. В этом случае хромосома есть вектор вещественных чисел. Их точность будет определяться исключительно разрядной сеткой той ЭВМ, на которой реализуется real-coded алгоритм. Длина хромосомы будет совпадать с длиной вектора-решения оптимизационной задачи, иначе говоря, каждый ген будет отвечать за одну переменную. Генотип объекта становится идентичным его фенотипу.
Вышесказанное определяет список основных преимуществ алгоритмов с непрерывными генами:
Использование непрерывных генов делает возможным поиск в больших пространствах (даже в неизвестных), что трудно делать в случае двоичных генов, когда увеличение пространства поиска сокращает точность решения при неизменной длине хромосомы.
Одной из важных черт непрерывных генетических алгоритмов является их способность к локальной настройке решений.
Использование непрерывных генетических алгоритмов для представления решений удобно, поскольку близко к постановке большинства прикладных задач. Кроме того, отсутствие операций кодирования/декодирования, которые необходимы в генетических алгоритмах с двоичным кодированием, повышает скорость работы алгоритма.
Как известно, появление новых особей в популяции канонического генетического алгоритма обеспечивают несколько биологических операторов: отбор, скрещивание и мутация. В качестве операторов отбора особей в родительскую пару здесь подходят любые известные из двоичных генетических алгоритмов: рулетка, турнирный, случайный. Однако операторы скрещивания и мутации не годятся: в классических реализациях они работают с битовыми строками. Нужны собственные реализации, учитывающие специфику real-coded алгоритмов.
Оператор скрещивания непрерывного генетического алгоритма, или кроссовер, порождает одного или нескольких потомков от двух хромосом. Собственно говоря, требуется из двух векторов вещественных чисел получить новые векторы по каким-либо законам. Большинство real-coded алгоритмов генерируют новые векторы в окрестности родительских пар. Для начала рассмотрим простые и популярные кроссоверы.
Пусть 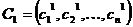 и
и 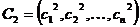 тАУ две хромосомы, выбранные оператором селекции для скрещивания. После формулы для некоторых кроссоверов приводится рисунок тАУ геометрическая интерпретация его работы. Предполагается, что
тАУ две хромосомы, выбранные оператором селекции для скрещивания. После формулы для некоторых кроссоверов приводится рисунок тАУ геометрическая интерпретация его работы. Предполагается, что 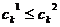 и
и 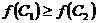 .
.
Плоский кроссовер (flat crossover): создается потомок 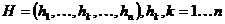 тАУ случайное число из интервала
тАУ случайное число из интервала 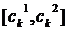 .
.
Простейший кроссовер (simple crossover): случайным образом выбирается число k из интервала 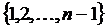 и генерируются два потомка
и генерируются два потомка 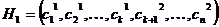 и
и 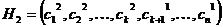 .
.
Арифметический кроссовер (arithmetical crossover): создаются два потомка 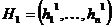 ,
, 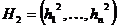 , где
, где 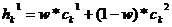 ,
, 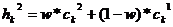 ,
, 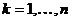 , w либо константа (равномерный арифметический кроссовер) из интервала
, w либо константа (равномерный арифметический кроссовер) из интервала 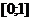 , либо изменяется с увеличением эпох (неравномерный арифметический кроссовер).
, либо изменяется с увеличением эпох (неравномерный арифметический кроссовер).
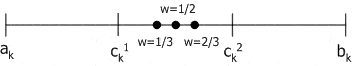
Геометрический кроссовер (geometrical crossover): создаются два потомка 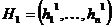 ,
, 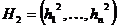 , где
, где 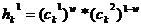 ,
, 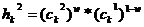 , w тАУ случайное число из интервала
, w тАУ случайное число из интервала 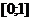 .
.
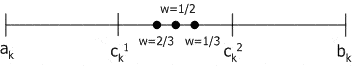
Смешанный кроссовер (blend, BLX-alpha crossover): генерируется один потомок 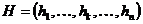 , где
, где 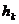 тАУ случайное число из интервала
тАУ случайное число из интервала 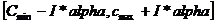 ,
, 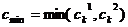 ,
,  ,
, 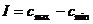 . BLX-0.0 кроссовер превращается в плоский.
. BLX-0.0 кроссовер превращается в плоский.
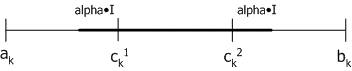
Линейный кроссовер (linear crossover): создаются три потомка 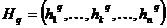 ,
, 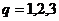 , где
, где 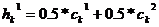 ,
, 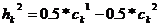 ,
, 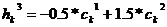 . На этапе селекции в этом кроссовере отбираются два наиболее сильных потомка.
. На этапе селекции в этом кроссовере отбираются два наиболее сильных потомка.

Дискретный кроссовер (discrete crossover): каждый ген 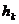 выбирается случайно по равномерному закону из конечного множества
выбирается случайно по равномерному закону из конечного множества 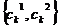 .
.

Расширенный линейчатый кроссовер (extended line crossover): ген 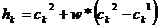 , w тАУ случайное число из интервала
, w тАУ случайное число из интервала 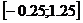 .
.

Эвристический кроссовер (WrightтАЩs heuristic crossover). Пусть 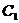 тАУ один из двух родителей с лучшей приспособленностью. Тогда
тАУ один из двух родителей с лучшей приспособленностью. Тогда 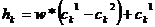 , w тАУ случайное число из интервала
, w тАУ случайное число из интервала 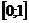 .
.

Нечеткий кроссовер (fuzzy recombination, FR-d crossover): создаются два потомка 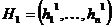 ,
, 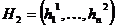 . Вероятность того, что в i-том гене появится число
. Вероятность того, что в i-том гене появится число 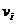 , задается распределением
, задается распределением 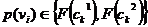 , где
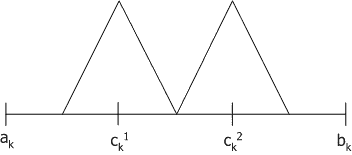
, где 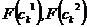 тАУ распределения вероятностей треугольной формы (треугольные нечеткие функции принадлежности) со следующими свойствами
тАУ распределения вероятностей треугольной формы (треугольные нечеткие функции принадлежности) со следующими свойствами  (
(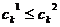 и
и 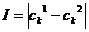 ):
):
| Распределение вероятностей | Минимум | Центр | Максимум |
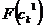
| 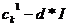
| 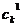
| 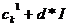
|
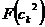
| 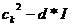
| 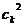
| 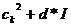
|
Параметр d определяет степень перекрытия треугольных функций принадлежности, по умолчанию 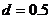 .
.
В качестве оператора мутации наибольшее распространение получили: случайная и неравномерная мутация (random and non-uniform mutation).
При случайной мутации ген, подлежащий изменению, принимает случайное значение из интервала своего изменения. В неравномерной мутации значение гена после оператора мутации рассчитывается по формуле:
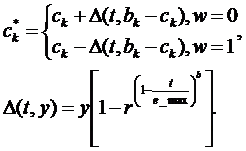
Сложно сказать, что более эффективно в каждом конкретном случае, но многочисленные исследования доказывают, что непрерывные генетические алгоритмы не менее эффективно, а часто гораздо эффективнее справляются с задачами оптимизации в многомерных пространствах, при этом более просты в реализации из-за отсутствия процедур кодирования и декодирования хромосом.
Рассмотренные кроссоверы исторически были предложены первыми, однако во многих задачах их эффективность оказывается невысокой. Исключение составляет BLX-кроссовер с параметром 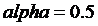 тАУ он превосходит по эффективности большинство простых кроссоверов. Позднее были разработаны улучшенные операторы скрещивания, аналитическая формула которых и эффективность обоснованы теоретически. Рассмотрим подробнее один из таких кроссоверов тАУ SBX.
тАУ он превосходит по эффективности большинство простых кроссоверов. Позднее были разработаны улучшенные операторы скрещивания, аналитическая формула которых и эффективность обоснованы теоретически. Рассмотрим подробнее один из таких кроссоверов тАУ SBX.
SBX (англ.: Simulated Binary Crossover) тАУ кроссовер, имитирующий двоичный. Был разработан в 1995 году исследовательской группой под руководством K. DebтАЩа. Как следует из его названия, этот кроссовер моделирует принципы работы двоичного оператора скрещивания.
SBX кроссовер был получен следующим способом. У двоичн
Вместе с этим смотрят:
"Инкарнация" кватернионов
*-Алгебры и их применение
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка