Математика (шпаргалка для экзамена)
Случайные события и их виды, понятие вероятности.
Случайным естественно называть такое событие, которое при заданном комплексе условий может, как произойти так и не произойти. Мера возможности осуществления такого события и есть его вероятность. Достоверное и невозможное события могут рассматриваться как крайние частные случаи случайных событий. Достоверным называют событие, которое обязательно произойдет при осуществлении определенного комплекса условий. Так, например, вода при нормальных атмосферных условиях и 0 замерзает. Невозможным является событие, которое при заданном комплексе условий никогда не произойдет. Таким образом, вероятность тАУ это шансы осуществления любого составного события, состоящего из нескольких элементарных.
Классическая формула подсчета вероятностей. Комбинаторика.
В общем случае, когда имеется n равновозможных элементарных событий w1,тАж,wn, вероятность любого составного события А, состоящего из m элементарных событий wi1,тАж,wim, определяется как отношение числа элементарных событий, благоприятствующих событию А, к общему числу элементарных событий, т.е. P(A)=m/n.
Понятие геометрической и статистической вероятностей.
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством: P=Длина l/Длина L. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством: P=площадь g/площадь G. Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V: P=Объем v/Объем V.
Пространство элементарных событий, операции над событиями.
При общем определении вероятности используется пространство элементарных событий, при этом элементарные события являются неопределяемым понятием, но относительно них предполагается, что в результате испытаний обязательно происходит одно из этих элементарных событий. Элементарные события попарно не совместны и образуют группу событий. События, не являющиеся элементарными, отождествляются с теми элементарными событиями, которые благоприятствуют ему, следовательно, случайные события можно рассматривать как подмножество в пространстве элементарных событий, поэтому операции над случайными событиями: объединение (сложение), пересечение (умножение), эквивалентность, отрицание тАУ полностью совпадают с соответствующими операциями над множествами. Операции объединения и пересечения множеств симметричны, т.е.
A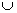 B = B
B = B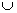 A A
A A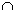 B = B
B = B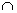 A
A
Аксиоматическое определение вероятности.
Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами: Аксиома 1. Для любого события A прин. S Р(А)>=0. Аксиома 2. Вероятность достоверного события равна единице Р (омега)=1. Аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: А прин. S, В прин. S, А*В=0, Р(А+В)=Р(А)+Р(В). Док-во: Событие А является подмножеством омега, так как А={wi1,тАж,wim},то, согласно конечной схеме, Р(А)=сумме по l от 1 до m рil, 0<=pil<=1, l=1,тАж,m, поэтому Р(А)>=0, т.е. условие аксиомы 1 выполняется. Условие аксиомы 2 выполняется, поскольку омега={w1,тАж,wn}и на основании того, что Р(А)=сумме по l от 1 до m рil, то Р(омега)=сумма по i от 1 до n pi=1. Условие аксиомы 3 также выполняется, так как оно представляет собой содержание теоремы сложения для конечной схемы. Итак, конечная схема является примером объекта, для которого выполняется система аксиом теории вероятностей.
Теорема сложения вероятностей.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ). Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС). Если два составных события А={wi1,тАж,wim}и В={wj1,тАж,wjk} являются несовместными, то вероятность объединенного события С=А+В равна сумме вероятностей этих двух событий.
Условная вероятность. Теорема умножения вероятностей.
1) Условная вероятность события А при условии В равна Р(А/B)=P(A*B)/P(B), Р(В)>0. 2) Событие А не зависит от события В, если Р(А/B)=P(A). Независимость событий взаимна, т.е. если событие А не зависит от В, то событие В не зависит от А. В самом деле при Р(А)>0 имеем Р(B/A)=P(A*B)/P(A)=P(A/B)*P(B)/P(A)=P(A)*P(B)/P(A)=P(B). Вытекает следующая формула умножения вероятностей: Р(А*В)=Р(А)*Р(В/A). Для независимых событий вероятность произведения событий равна произведению их вероятностей: Р(А*В)=Р(А)*Р(В). 3) События А1,А2,тАж,Аn образуют полную группу событий, если они попарно несовместны и вместе образуют достоверное событие, т.е. Аi*Aj=0, i не=j, U по i от 1 до n Аi=омега.
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)*Ра(В). В частности для независимых событий Р(АВ)=Р(А)*Р(В), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Формула полной вероятности.
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В1,В2,тАж,Вn , образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А: Р(А)=Р(В1)*Рb1(A)+P(B2)*Pb2(A)+тАж+P(Bn)=1. Если события А1,тАж,Аn, P(Ai)>0 образуют полную группу событий, то вероятность события В может быть представлена как сумма произведений безусловных вероятностей событий полной группы на условные вероятности события В: Р(В)=сумма по i от 1 до n P(Ai)*P(B/Ai).
Формула Байеса.
Из формулы полной вероятности легко получить формулу Байеса: для события В с Р(В)>0 и для системы попарно несовместных событий Аi, P(Ai)>0, B прин. U по i от 1 до n Аi . Р(Аk/B)=P(Ak)*P(B/Ak)/сумма по i от 1 до n P(Ai)*P(B/Ai).
Определение дискретной случайной величины. Ряд распределения.
Случайной величиной называется функция Х=Х(w), определенная на множестве элементарных событий омега, w прин. омега. С.В. дискретна, если она принимает значения только из некоторого дискретного множества, или, точнее, С.В. дискретна, если существует конечное или счетное множество чисел х1, х2, х3,тАж таких, что P{X=xn}=pn>=0, n=1,2,3тАж и р1+р2+р3+тАж=1. Закон распределения Д.С.В. Х определен, если известны все хn и вероятности рn=P{X=xn} такие, что р1+р2+р3+тАж=1. Если составить таблицу, в верхней строке которой поместить значения Д.С.В. , а в нижней тАУ соответствующие вер-ти, то получим ряд распределения С.В.
Функция распределения С.В. и ее свойства.
Функция распределения Fx(x) C.В. Х определяется формулой Fx(x)=P{w:X(w)=F(x1),если х2>х1. 4) Р{X>=x}=1 тАУ F(x). 5) Если х стремится к бесконечности, то F(x) к 1. 6) Если х стремится к тАУ бесконечности, то F(x) к нулю. 7) Ф.Р. непрерывна слева, т.е. lim при дельта стрем. к +0 F(x тАУ дельта)=F(x).
Математическое ожидание Д.С.В. и его свойства.
Мат. Ожиданием Д.С.В. называют сумму произведений всех ее возможных значений на их вероятности: М(Х)=х1р1+х2р2+тАж+хnpn. Если Д.С.В. принимает счетное множество возможных значений, то М(Х)=сумма по i от 1 до бесконечности xipi, причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Мат. ожидание обладает следующими свойствами: 1) Мат. ожидание постоянной величины равно самой постоянной: М(С)=С. 2) Постоянный множитель можно выносить за знак мат. ожидания: М (СХ)=СМ (Х). 3) Мат. ожидание произведения взаимно независимых С.В. равно произведению мат. ожиданий сомножителей: М (Х1,Х2тАжХn)=M(X1)*M(X2)тАжM(Xn). 4) Мат. ожидание суммы С.В. равно сумме мат. ожиданий слагаемых: М (Х1+Х2+Х3+тАж+Хn)=M(X1)+M(X2)+M(X3)+тАж+M(Xn).
Дисперсия Д.С.В. и ее свойства.
Дисперсией С.В. Х называют мат. ожидание квадрата отклонения С.В. от ее мат. ожидания: D (X)=M[X тАУ M(X)]*2. Дисперсию удобно вычислять по формуле: D (X)=M (X*2) тАУ [M (X)]*2. Дисперсия обладает следующими свойствами: 1) Д. постоянной равна нулю: D(C)=0. 2) Постоянный множитель можно выносить за знак Д., предварительно возведя его в квадрат: D (CX)=C*2D(X). 3) Д. суммы независимых С.В. равна сумме Д. слагаемых: D (X1+X2+тАж+Xn) =D(X1)+D(X2)+тАж+D(Xn).
Схема опытов Бернулли. Биномиальный закон распределения.
Биномиальным называют закон распределения Д.С.В. Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р, вер-ть возможного значения Х=k (числа k появлений события) вычисляют по формуле Бернулли: Pn (k)=Cn*k p*k q*n-k.
Закон распределения Пуассона, пуассоновское распределение как предельное для биномиального.
Если число испытаний велико, а вероятность р появления события в каждом испытании очень мала, то используют приближенную формулу: Pn (k)=лямда*k e*-лямда/k!, где к тАУ число появлений события в n независимых испытаниях, лямда=np (среднее число появлений события в n испытаниях), и говорят, что С.В. распределена по закону Пуассона.
Геометрический закон распределения Д.С.В.
С.В. Х имеет геометрическое распределение, если Pm=P{X=m}=q*m p, m=0,1,2,тАж, 0
Определение непрерывной С.В. Плотность распределения и ее свойства.
С.В. Х называется непрерывной, если существует неотрицательная функция рх(х) такая, что при любых х функцию распределения Fx(x) можно представить в виде: Fx(x)=интеграл от тАУбесконечности до х px(y)dy. Рассматривают только такие С.В., для которых рх(х) непрерывна всюду, кроме, может быть, конечного числа точек. Плотностью распределения вероятностей непрерывной С.В. называют первую производную от функции распределения: f(x)=FтАЩ(x). Вероятность того, что Н.С.В. Х примет значение, принадлежащее интервалу (а,b), определяется равенством P(a=0. 2) Несобственный интеграл от плотности распределения в пределах от тАУбесконечности до бесконечности равен единице: интеграл от тАУбесконечности до бесконечности f(x)dx=1.
Математическое ожидание Н.С.В. и его свойства.
Мат. ожидание Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: М(Х)=интеграл от тАУбесконечности до бесконечности хf(x)dx, где f(x) - плотность распределения С.В. Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (а,b), то М(Х)=интеграл от а до b xf(x)dx. Все свойства мат. ожидания, указаны выше, для Д.С.В. Они сохраняются и для Н.С.В.
Дисперсия Н.С.В. и ее свойства.
Дисперсия Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: D(X)=интеграл от тАУбесконечности до бесконечности [x-M(X)]*2f(x)dx, или равносильным равенством: D(X)=интеграл от тАУбесконечности до бесконечности x*2f(x)dx тАУ [M(X)]*2. В частности, если все возможные значения х принадлежат интервалу (a,b),то D(X)=интервал от а до b [x тАУ M(X)]*2f(x)dx,или D(X)=интеграл от a до b x*2f(x)dx тАУ [M(X)]*2. Все свойства дисперсии Д.С.В. сохраняются и для Н.С.В.
Равномерный закон распределения.
Равномерным называют распределение вероятностей Н.С.В. Х, если на интервале (а,b), которому принадлежат все возможные значения Х, плотность сохраняет постоянное значение, а именно f(x)=1/(b-a); вне этого интервала f(x)=0. Нетрудно убедиться, что интеграл от тАУбесконечности до бесконечности р(х)dx=1. Для С.В., имеющей равномерное распределение , вероятность того, что С.В. примет значения из заданного интервала (х,х+дельта) прин. [a,b], не зависит от положения этого интервала на числовой оси и пропорциональна длине этого интервала дельта: P{xb.
Показательный закон распределения.
Н.С.В. Х, принимающая неотрицательные значения, имеет показательное распределение с параметром лямда, если плотность распределения С.В. при x>=0 равна р(х)=лямда*е в степени - лямда*х и при x<0 р(х)=0. Функция распределения С.В. Х равна F(x)=интеграл от тАУбесконечности до х р(t)dt=0, при x<=0,1-е в степени тАУлямда*х при x>0.
Нормальный закон распределения.
Н.С.В. Х имеет нормальное распределение вероятностей с параметром а и сигма>0, если ее плотность распределения имеет вид: р(х)=1/(корень квадратный из 2пи *сигма) * е в степени тАУ1/2*(x-a/сигма)*2. Если Х имеет нормальное распределение, то будем кратко записывать это в виде Х прибл. N(a,сигма). Так как фи(х)=1/(корень из 2пи)*е в степени тАУх*2/2 тАУ плотность нормального закона распределения с параметрами а=0 и сигма=1, то функция Ф(х)=1/(корень из 2пи)* интеграл от тАУбесконечности до х е в степени тАУt*2/2dt, с помощью которой вычисляется вероятность P{a<=мюn-np/(корень из npq)<=b}, является функцией распределения нормального распределения с параметрами а=0, сигма=1.
Функция Лапласа, ее свойства; вероятность попадания в интервал для нормального распределения С.В.
СВ называется нормально распределенной, если ее плотность распределения имеет вид
f(x)=(1/sÖ(2p))*e-(x-a)2/2s2; s>0.
Функцией Лапласа называется функция вида(Z=x-a/s)
Ф(Х)= 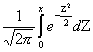 . АргументтАФпеременная верхнего предела.
. АргументтАФпеременная верхнего предела.
Св-ва;
Функция Ф(х)тАФнечетная, т.е. Ф(-х_=-Ф(х)
Функция монотонно возрастает, т.е. х2>x1 следовательно, Ф(х2)>Ф(х1)
Ф(х2)=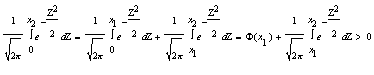 тАФ> Ф(х2)>Ф(х1)
тАФ> Ф(х2)>Ф(х1)
3.Ф(+¥)=0,5.Доказательство.
Ф(¥)=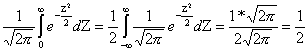
Ф-ция Ф(Х) возрастает и стремится к 0,5.
Вероятность попадания в интервал для НРСВ.
Пусть xтАФНРСВ с пар. а и s(s>0).
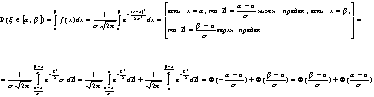
Неравенство Чебышева.
Если известна дисперсия С.В., то с ее помощью можно оценить вероятность отклонения этой величины на заданное значение от своего мат. ожидания, причем оценка вероятности отклонения зависит лишь от дисперсии. Соответствующую оценку вероятности дает неравенство Чебышева. Неравенство Чебышева является частным случаем более общего неравенства, позволяющего оценить вероятность события, состоящего в том, что С.В. Х превзойдет по модулю произвольное число t>0. P{|X тАУ MX|>=t}<=1/t*2 M(X тАУ MX)*2=1/t*2 DX тАУ неравенство Чебышева. Оно справедливо для любых С.В., имеющих дисперсию; оценка вероятности в нем не зависит от закона распределения С.В. Х.
Теоремы Маркова и Чебышева.
Теорема Чебышева. Если последовательность попарно независимых С.В. Х1,Х2,Х3,тАж,Xn,тАж имеет конечные мат. ожидания и дисперсии этих величин равномерно ограничены (не превышают постоянного числа С), то среднее арифметическое С.В. сходится по вероятности к среднему арифметическому их мат. ожиданий, т.е. если эпселен тАУ любое положительное число, то: lim при n стремящемся к бесконечности P(|1/n сумма по i от 1 до n Xi тАУ 1/n сумма по i от 1 до n M(Xi)|<эпселен)=1. В частности, среднее арифметическое последовательности попарно независимых величин, дисперсии которых равномерно ограничены и которые имеют одно и тоже мат. ожидание а, сходится по вероятности к мат. ожиданию а, т.е. если эпселен тАУ любое положительное число, то: lim при n стремящемся к бесконечности P(|1/n сумма по i от 1 до n Xi тАУ a|<эпселен)=1. Теорема Маркова. P{|X|>=t}<=1/tM|X| - неравенство Маркова. Док-во: 1) Для Д.С.В. Х. Пусть Х тАУ Д.С.В., Р{X=xi}=pi, i=1,2,3,тАж,сумма по i от 1 до бесконечности pi=1. Тогда вероятность события {|X|>=t} равна сумме вероятностей pi, для которых xi находится вне промежутка (-t,t). Очевидно, для всех xi, не принадлежащих промежутку (-t,t), имеет место неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|=t, равна сумме интегралов от плотности вероятности по промежуткам (-бесконечность, -t) и (t,бесконечность). На этих промежутках |x|/t*t>=1. Так как |x|/t*p(x)>=0, то интеграл от тАУt до t по |x|/t*p(x)dx>=0. Воспользовавшись формулой M|X|=интеграл от тАУбесконечности до бесконечности |x| p(x) dx, в результате преобразований получаем неравенство Маркова.
Центральная предельная теорема, следствия (теорема Муавра-Лапласа).
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0
Двумерная С.В. Двумерная функция распределения и ее свойства.
Двумерной называют С.В. (Х,Y), возможные значения которой есть пары чисел (x,y). Составляющие Х и Y, рассматриваемые одновременно, образуют систему двух С.В. Дискретной называют двумерную величину, составляющие которой дискретны. Непрерывной называют двумерную величину, составляющие которой непрерывны. Законом распределения Д.С.В. называют соответствие между возможными значениями и их вероятностями. Функция распределения вероятностей Д.С.В. называют функцию F(X,Y), определяющую для каждой пары чисел (х,y) вероятность того, что Х примет значение, меньшее х, при этом Y примет значение, меньшее y: F(x,y)=P(X=F(x1,y), если х2>x1. F(x,y2)>=F(x,y1), если y2>y1. 3) Имеют место предельные соотношения: 1) F(-бесконечность, у)=0, 2) F(x,-бесконечность)=0, 3) F(-бесконечность, -бесконечность)=0, 4) F(бесконечность, бесконечность)=1. 4) а) при у=бесконечность функция распределения системы становится функцией распределения составляющей Х: F(x,бесконечность)=F1(x). Б) при х=бесконечность функция распределения системы становится функцией распределения составляющей У: F(бесконечность, у)=F2(y).
Условные и безусловные законы распределения компонент двумерной С.В.
Условные. 1) Для дискретной двумерной С.В. Пусть составляющие X и Y дискретны и имеют соответственно следующие возможные значения: x1,x2,тАж,xn; y1,y2,тАж,ym. Условным распределением составляющей Х при Y=yj (j сохраняет одно и то же значение при всех возможных значениях Х) называют совокупность условных вероятностей p(x1|yj), p(x2|yj),тАж,p(xn|yj). Аналогично определяется условное распределение Y. Условные вероятности составляющих Х и Y вычисляют соответственно по формулам: p(xj|yi)=p(xi,yj)/p(yj), p(yj|xi)=p(xi,yj)/p(xi).
Корреляционный момент, коэффициент корреляции.
Корреляционным моментом СВ x и h называется мат. ожидание произведения отклонений этих СВ. mxh=М((xтАФМ(x))*(hтАФМ(h)))
Для вычисления корреляционного момента может быть использована формула:
mxh=М(x*h)тАФМ(x)*М(h) Доказательство: По определению mxh=М((xтАФМ(x))*(hтАФМ(h))) По свойству мат. ожидания
mxh=М(xhтАФМ(h)тАФhМ(x)+М(x)*М(h))=М(xh)тАФМ(h)*М(x)тАФМ(x)*М(h)+М(x)*М(h)=М(xh)тАФМ(x)*(h)
Предполагая, что x и h независимые СВ, тогда mxh=М(xh)тАФМ(x)*М(h)=М(x)*М(h)тАФМ(x)*М(h)=0; mxh=0. Можно доказать, что если корреляционный момент=0, то СВ могут быть как зависимыми, так и независимыми. Если mxh не равен 0, то СВ x и h зависимы. Если СВ x и h зависимы, то корреляционный момент может быть равным 0 и не равным 0. Можно показать, что корреляционный момент характеризует степень линейной зависимости между составляющими x и h. При этом корреляционный момент зависит от размерности самих СВ. Чтобы сделать характеристику линейной связи x и h независимой от размерностей СВ x и h, вводится коэффициент корреляции:
Кxh=mxh/s(x)*s(h) Коэффициент корреляции не зависит от разностей СВ x и h и только показывает степень линейной зависимости между x и h, обусловленную только вероятностными свойствами x и h. Коэффициент корреляции определяет наклон прямой на графике в системе координат (x,h) Свойства коэффициента корреляции.
-1<=Кxh<=1
Если Кxh =В±1, то линейная зависимость между x и h и они не СВ.
Кxh>0, то с ростом одной составляющей, вторая также в среднем растет.
Кxh<0, то с убыванием одной составляющей, вторая в среднем убывает.
D(xВ±h)=D(x)+D(h)В±2mxh
Доказательство.
D(xВ±h)=M((xВ±h)2)тАФM2(xВ±h)=M(x2В±2xh+h2)тАФ(M(x)В±M(h))2=M(x2)В±2M(xh)+M(h2)тАФ+M2(x)+2M(x)*M(h)тАФM2(h)=D(x)+D(h)В±2(M(xh))тАФM(x)*M(h)=D(x)+D(h)В±2mxh
Предмет математической статистики. Генеральная совокупность и выборка.
Мат. статистика опирается на теорию вероятностей, и ее цель тАУ оценить характеристики генеральной совокупности по выборочным данным. Генеральной совокупностью называется вероятностное пространство {омега,S,P} (т.е. пространство элементарных событий омега с заданным на нем полем событий S и вероятностями Р) и определенная на этом пространстве С.В. Х. Случайной выборкой или просто выборкой объема n называется последовательность Х1,Х2,тАж,Xn, n независимых одинаково распределенных С.В., распределение каждой из которых совпадает с распределением исследуемой С.В. Х. Иными словами, случайная выборка тАУ это результат n последовательных и независимых наблюдений над С.В. Х, представляющей генеральную совокупность.
Выборочное оценивание функции распределения и гистограмма.
Наиболее полная характеристика С.В. тАУ это ее Ф.Р. Пусть х1,х2,тАж,xn тАУ выборка из генеральной совокупности, представленной С.В. Х. Рассмотрим, как оценить Ф.Р. F(x) этой С.В., о которой известно только, что она непрерывна. Чтобы построить оценку F^n(x) Ф.Р. F(x), обычно располагают наблюдения xi в порядке их возрастания, т.е. находят вначале X*1=minXi, затем следующее по величине наблюдаемое значение и т.д.; если есть одинаковые значения, то их расположение не играет никакой роли. Последовательность неубывающих величин Х*1<=X*2<=X*n, полученных после упорядочения выборки, называется вариационным рядом. Существует статистическое и эмпирическое распределение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/h (плотность частоты), где ni тАУ сумма частот вариант попавших в i-ый интервал.
Точечные оценки числовых характеристик. Основные определения. Метод моментов.
Статистической оценкой K * неизвестного параметра K теоретического распределения называют функцию f(X1,X2,тАж,Xn) от наблюдаемых С.В. X1,X2,тАж,Xn. Точечной называют статистическую оценку, которая определяется одним числом K *=f(x1,x2,тАж,xn), где х1,х2,тАж,xn тАУ результаты n наблюдений над количественным признаком Х (выборка). Несмещенной называют точечную оценку, мат. ожидание которой равно оцениваемому параметру при любом объеме выборки. Смещенной называют точечную оценку, мат. ожидание которой не равно оцениваемому параметру. Несмещенной оценкой генеральной средней (мат. ожидания) служит выборочная средняя: Хв=(сумма по i от 1 до k nixi)/n, где xi тАУ варианта выборки, ni тАУ частота варианты xi, n=сумма по i от 1 до k ni тАУ объем выборки. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия: Dв=(сумма по i от 1 до k ni(Хi-Xв)*2)/n. Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия: s*2=n/n-1*Dв=сумма ni(xj тАУ Xв)*2/n-1. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: v1=M1. Учитывая, что v1=M(X) и М1=Хв, получим М(Х)=Хв. Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Учитывая, что v1=M(X),M1=Хв,мю=D(X),m2=Dв, имеем систему: М(Х)=Хв, D(X)=Dв.
Метод наибольшего правдоподобия.
Метод наибольшего правдоподобия точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров. Д.С.В. Пусть Х тАУ Д.С.В., которая в результате n опытов приняла возможные значения х1,х2,тАж,xn. Допустим, что вид закона распределения величины Х задан, но неизвестен параметр K, которым определяется этот закон; требуется найти его точечную оценку K*=K (x1,x2,тАж,xn). Обозначим вероятность того, что в результате испытания величина Х примет значение xi через р(xi;K). Функцией правдоподобия Д.С.В. Х называют функцию аргумента K: L (x1,x2,тАж,xn;K)=p(x1;K)*p(x2;K)тАжp(xn;K). Оценкой наибольшего правдоподобия параметра K называют такое его значение K*, при котором функция правдоподобия достигает максимума. Функции L и lnL достигают максимума при одном и том же значении K, поэтому вместо отыскания максимума функции L ищут, что удобнее, максимум функции lnL. Н.С.В. Пусть Х тАУ Н.С.В., которая в результате n испытаний приняла значения х1,х2,тАж,xn. Допустим, что вид плотности распределения тАУ функции f(x) тАУ задан, но неизвестен параметр K, которым определяется эта функция. Функцией правдоподобия Н.С.В. Х называют функцию аргумента K: L(x1,x2,тАж,xn;K)=f(x1;K)*f(x2;K)тАжf(xn;K).
Интервальные оценки числовых характеристик. Доверительный интервал. Основные определения.
Интервальной называют оценку, которая определяется двумя числами тАУ концами интервала, покрывающего оцениваемый параметр. Доверительный интервал тАУ это интервал, который с заданной надежностью гамма покрывает заданный параметр. 1. Интервальной оценкой с надежностью гамма мат. ожидания а нормально распределенного количественного признака Х по выборочной средней Хв при известном среднем квадратическом отклонении сигма генеральной совокупности служит доверительный интервал: Хв тАУ t(сигма/корень из n)1. 3. Интервальной оценкой ( с надежностью гамма) неизвестной вероятности р биномиального распределения по относительной частоте w служит доверительный интервал ( с приближенными концами р1 и р2).
Доверительный интервал для мат. ожидания при известной дисперсии.
K^=X=1/n сумма по i от 1 до n Xi является наилучшей несмещенной оценкой для мат. ожидания МХ=K нормального распределения f(x,K)=1/(корень из 2пи сигма в квадрате)*е тАУ(х-K)*2/(2сигма в квадрате) по выборке объема n. Пусть дисперсия Хi Dxi=сигма в квадрате известна, где сигма в квадрате тАУ некоторое конкретное число. Предполагается, что для нормально распределенного признака x, дисперсия которого известна равна s2. По выборке объема n получены выборочные значения x1, x2, .. , xn. Требуется получить интервальную оценку неизвестного нам математического ожидания этого признака. M |x| > a заданной надежности j. Сначала рассчитываем точечную оценку математического ожидания:
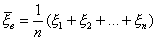 ; Будем считать, что x1, x2, .. , xn разные СВ, но распределенные по одному и тому же закону и математическое ожидание.
; Будем считать, что x1, x2, .. , xn разные СВ, но распределенные по одному и тому же закону и математическое ожидание.
M(xi) = a; Д(xi) = s2; 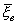 - значение СВ
- значение СВ 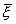 и тогда
и тогда 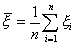 , тогда
, тогда
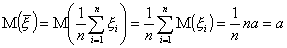

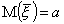 Доказательство несмещенности точечной оценки
Доказательство несмещенности точечной оценки 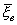
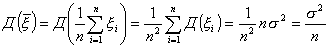
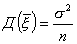 Вывод:
Вывод: 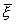 - нормально распределенная СВ,
- нормально распределенная СВ, 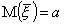 ,
, 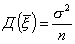 , тогда чтобы найти вероятность заданного отклонения P(|a тАУ
, тогда чтобы найти вероятность заданного отклонения P(|a тАУ 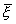 | < d) = j
| < d) = j
P(|a тАУ 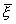 | < d) = 2Ф(
| < d) = 2Ф(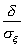 ) = 2Ф(
) = 2Ф(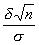 ), где
), где 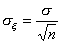 ; Ф(
; Ф(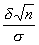 ) =
) = 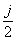
По таблице для функции Лапласа по значению функции равной 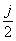 находим значение аргумента
находим значение аргумента 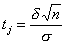 ;
; 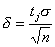 ; Вместо
; Вместо 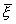 обозначаем
обозначаем 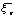 .; P(|a тАУ
.; P(|a тАУ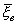 | < d) = P(-d< a -
| < d) = P(-d< a - 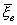 < d) = P(
< d) = P(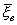 - d < a <
- d < a < 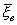 + d) = j
+ d) = j
(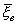 - d;
- d; 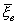 + d) тАУ доверительный интервал.
+ d) тАУ доверительный интервал.
Проверка гипотез. Ошибки первого и второго рода. Мощность критерия.
В статистике рассматриваются гипотезы двух типов:
Параметрические тАУ гипотезы о значении параметра известного распределения;
Непараметрические тАУ гипотезы о виде распределения.
Обычно выделяют основную гипотезу тАУ нулевую (H0). Пример: математическое ожидание признака x, который распределен по нормальному закону и дисперсия его известна, а H0: M(x) = a. Предполагаем, что известна дисперсия Конкурирующая гипотеза имеет вид: H1: M(x) ¹ a;
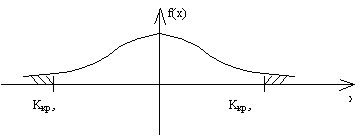 H1: M(x) > a, либо H1: M(x) = a1. Для проверки гипотез используются критерии, и они представляют собой специальным образом подобранные СВ, k тАУ точечный или приближенный закон, который известен.
H1: M(x) > a, либо H1: M(x) = a1. Для проверки гипотез используются критерии, и они представляют собой специальным образом подобранные СВ, k тАУ точечный или приближенный закон, который известен.
Обычно предполагается, что если гипотеза Н0 выполняется, то вычисляемая по выборочным данным kнабл. Этого критерия и гипотеза Н0 принимается, если kнабл.Î (kкритич. левостор.; kкритич. правостор.) Если kнабл. попадает в критическую область (все остальные значения k Î(- ¥ ; kкритич. лев.) È (kкритич. прав. ; ¥), то гипотеза Н0 отвергается и принимается конкурирующая гипотеза Н1. При этом возможны ошибки двух типов: Первого рода: что гипотеза Н0 отвергается, в то время, как она верна. Вероятность этой ошибки: P(H1/H0) = a - уровень значимости критерия. Критерий подбирается так, чтобы a была как можно меньше. Второго рода: что отвергается гипотеза Н1, в то время, как она верна. b = P(H0/H1) Мощностью критерия тАУ (1-b) - вероятность попасть точке-выборке в критическое множество, когда верна конкурирующая гипотеза.
1-b = P(H1/H1)
37. Проверка гипотезы о равенстве генеральных средних при известных дисперсиях. Признак x и h распределены нормально с известными дисперсиями.
Пусть по выборкам x1, x2, .. , xn объема n, h1, h2, .. , hm объема m, получены выборочные средние значения (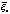 ;
; 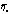 ). Выдвигается гипотеза о равенстве генеральных средних: H0: M(x) = M(h); При конкурирующей гипотезе:
). Выдвигается гипотеза о равенстве генеральных средних: H0: M(x) = M(h); При конкурирующей гипотезе:
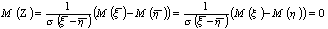
H1: M(x) ¹ M(h); В качестве проверки гипотезы выбираем новую СВ
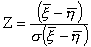
;
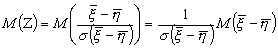
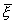 - СВ:
- СВ:
Д(Z)- дисперсия Д((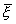 -
- 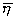 )/s(
)/s(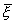 -
-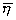 )) =
)) = 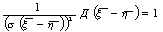
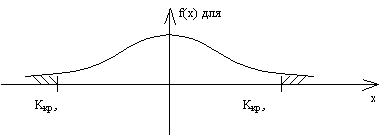
M(Z) = 0; Д(Z) = 1. Для того, чтобы выбрать Zкр. и при заданном уровне значимости a, определить принимается или не принимается основная гипотеза, найти вероятности.
P(0 < Z < Zкр.) + P(Z > Zкр. прав.) = ½ Ф(Zкр.) + a/2 = ½ Ф(Zкр. прав.) = ½ - a/2
Zнабл. = 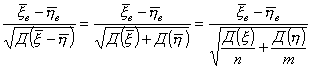
|Zнабл.| < Zкр.прав. Þ Н0 |Zнабл.| > Zкр.прав. Þ Н0 отвергается.
38. Проверка гипотезы о равенстве генеральных средних при неизвестных дисперсиях.
Пусть x и h нормально распределенные СВ, предполагается, что неизвестны, но равны между собой дисперсии. x1, x2, .. , xn h1, h2, .. , hm
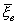 ;
; 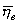 : Н0: М(x) = М(h) Н1: М(x) ¹ М(h)
: Н0: М(x) = М(h) Н1: М(x) ¹ М(h)
Для проверки гипотезы Н0, вводится СВ t, которая представляет собой
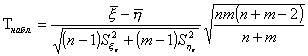
Теоретическое обозначение признака; СВ Т распределена по закону Стъюдента, зависит от первого параметра, который называется числом степеней свободы (k).
k = n + m тАУ 2 (по таблице для распределения Стъюдента при заданном значении k и уровне значимости a в зависимости от вида альтернативной и конкурирующей гипотезы, находятся либо односторонние tкр., либо двухсторонние tкр.).
Ткр. прав. = - Ткр. лев. | Тнабл. | < Ткр. двуст. Þ Н0 | Тнабл. | > Ткр. двуст. Þ Н0 отвергается.
42. Марковские случайные процессы. Размеченный граф состояний.
Предположим, что дана система S. Предп., что состояние этой сис-мы хар-ся параметрами состояний. Если состояние системы меняется во времени случайно, то говорят, что в сис-ме протекает случайный процесс. Сис-ма тАФаудитория. Для хар-ки состояния используется параметртАФчисло студентов, тогда эта система с дискретными состояниями. Будем рассматривать системы с дискретными состояниями и непрерывным t: сис-ма мгновенно в произвольные сегменты t скачками меняет состояние. Если параметр t принимает
Вместе с этим смотрят:
"Инкарнация" кватернионов
*-Алгебры и их применение
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка