Определитель произведения прямоугольных матриц. Теорема Коши-Бине
Курсовая работа
Выполнила студентка II курса группы ПМИ Решоткина Наталья Николаевна
Мурманский Государственный Педагогический Университет
Мурманск 2007
Введение
При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.
Цель данной работы: теоретическое обоснование и необходимость практического применения теоремы Коши-Бине:
Пусть  ,
,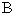 -
- 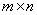 и
и 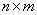 -матрицы соответственно,
-матрицы соответственно, 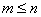 и
и 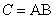
Тогда 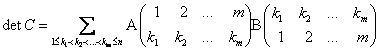
Другими словами, при 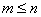 определитель матрицы
определитель матрицы 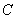 является суммой произведений всевозможных миноров порядка
является суммой произведений всевозможных миноров порядка 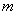 в
в  на соответствующие миноры матрицы
на соответствующие миноры матрицы 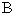 того же самого порядка
того же самого порядка
Работа состоит из четырех глав, содержит заключение, список литературы и приложение программы для теоремы Коши-Бине. В главе I рассматриваются элементы линейной алгебры тАУ матрицы, операции над матрицами и свойства сложения матриц, и умножения на скаляр. Глава II посвящается умножению матриц и его свойств, а также транспонирование произведения двух матриц. В главе III рассматриваются обратимые и элементарные матрицы. В главе IV вводиться понятие определителя квадратной матрицы, рассматриваются свойства и теоремы об определителях, а также приводится доказательство теоремы Коши-Бине, что является целью моей работы. В дополнение прилагается программа показывающая механизм нахождения определителя произведения двух матриц.
Глава I
Вз 1 Определение, обозначения и типы матриц
Мы определяем матрицу как прямоугольную таблицу чисел:
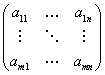
Где элементы матрицы aij (1≤i≤m, 1≤j≤n)-числа из поля 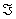 .Для наших целей поле
.Для наших целей поле 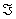 будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы
будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы 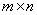 , где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.
, где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.
Каждой 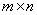 матрице
матрице  с элементами aij соответствует n×m матрица с элементами aji . Она называется транспонированной к
с элементами aij соответствует n×m матрица с элементами aji . Она называется транспонированной к  и обозначается через
и обозначается через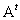 . Видно, что
. Видно, что 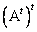 =
= . Строки матрицы
. Строки матрицы  становятся столбцами в
становятся столбцами в 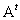 и столбцы матрицы
и столбцы матрицы  становятся строками в
становятся строками в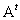 .
.
Матрица называется нулевой если все элементы равны 0:
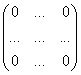
Матрица называется треугольной если все ее элементы, расположенные ниже главной диагонали равны 0

Треугольная матрица называется диагональной, если все элементы расположенные вне главной диагонали равны 0

Диагональной матрица называется единичной, если все элементы расположенные на главной диагонали равны 1
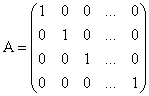
Матрица, составленная из элементов, находящихся на пересечении нескольких выбранных строк матрицы  и нескольких выбранных столбцов, называется субматрицей для матрицы
и нескольких выбранных столбцов, называется субматрицей для матрицы  . Если
. Если 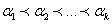 -номера выбранных строк и
-номера выбранных строк и 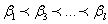 -номера выбранных столбцов, то субматрица это
-номера выбранных столбцов, то субматрица это

В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.
Вз2 Операции над матрицами
Определим следующие операции:
Сумма двух 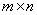 матриц
матриц  , и
, и 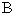 с элементами
с элементами 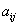 и
и 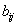 есть
есть 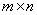 матрица С с элементами
матрица С с элементами 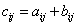 , запишем это как
, запишем это как 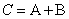
Произведение матрицы  на число
на число 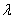 поля
поля 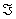 есть матрица С с элементами
есть матрица С с элементами 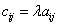 , запишем как
, запишем как 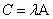 .
.
Произведение 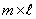 матрицы
матрицы  на
на 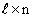 матрицу
матрицу 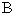 есть
есть 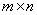 матрица С с элементами
матрица С с элементами 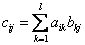 , запишем
, запишем 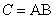
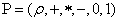 поле скаляров, рассмотрим
поле скаляров, рассмотрим 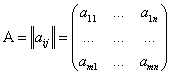 , где
, где 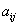 элемент матрицы
элемент матрицы  , расположенный в
, расположенный в 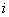 -строке
-строке 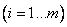 ,
, 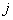 -столбце
-столбце 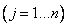 . Размерность матрицы
. Размерность матрицы 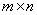 .Если
.Если 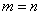 , то
, то  -квадратная матрица порядка
-квадратная матрица порядка 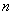 . Множество
. Множество 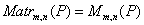 -это множество всех
-это множество всех 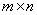 матриц над полем
матриц над полем 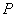 .
.
Опр. Две матрицы равны, если они имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы. Другими словами: 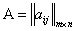 равна матрице
равна матрице 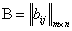 , т.е
, т.е 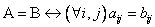
Опр. Пусть 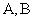 -это матрицы одинаковой размерности
-это матрицы одинаковой размерности 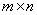 . Суммой матриц
. Суммой матриц  и
и 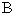 называется
называется 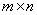 матрица у которой в
матрица у которой в 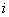 строке,
строке, 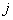 столбце расположен элемент
столбце расположен элемент 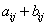 , т.е.
, т.е. 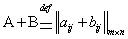 . Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:
. Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:
Пример:
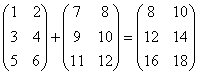
Опр. Пусть 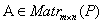 ,
, 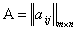 ,
, 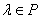 . Произведение скаляра
. Произведение скаляра 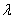 на матрицу
на матрицу  называется
называется 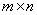 у которой в
у которой в 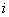 строке,
строке, 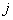 столбце расположен элемент
столбце расположен элемент 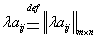 . Другими словами: Чтобы скаляр
. Другими словами: Чтобы скаляр 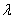 умножить на матрицу
умножить на матрицу  нужно все элементы матрицы
нужно все элементы матрицы  умножить на скаляр
умножить на скаляр 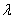 .
.
Определение. Противоположной к матрице  называется матрица
называется матрица 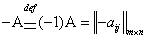
Свойства сложения и умножения матриц на скаляры:
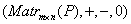 -абелева группа
-абелева группа
1) Сложение матриц 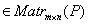 ассоциативно и коммутативно.
ассоциативно и коммутативно.
2) 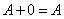
3) 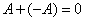
а) 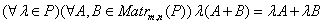
б) 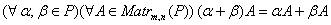
4) 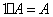
Глава II
Вз1 Умножение матриц
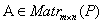 ,
, 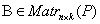
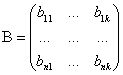
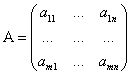 ,
, 
Опр. Произведением 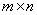 матрицы
матрицы  на
на 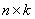 матрицу
матрицу 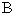 называется
называется 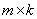 матрица
матрица 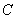 .
. 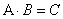 , где
, где 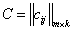
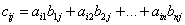 , где
, где 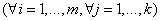
Говорят, что 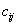 есть скалярное произведение
есть скалярное произведение 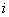 -строки матрицы
-строки матрицы  на
на 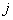 -столбец матрицы
-столбец матрицы 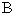 .
.
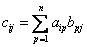 , где
, где 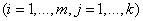
Пример:

Вз2 Свойства умножения матриц
Умножение матриц ассоциативно:
1) 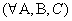
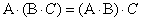 , если определены произведения матриц
, если определены произведения матриц 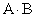 и
и 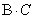
Доказательство:
Пусть 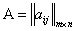 , так как определено
, так как определено 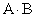 , то
, то 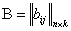 и определено
и определено 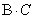 , то
, то 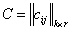
Определим матрицы:
а) 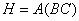
б) 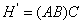
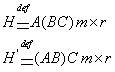 (1) матрицы, тогда
(1) матрицы, тогда 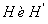 имеют одинаковую размерность
имеют одинаковую размерность
2) Покажем, что на одинаковых местах в матрицах 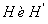 расположены одинаковые элементы
расположены одинаковые элементы
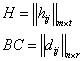 из равенства (1)
из равенства (1) 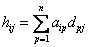 (2),
(2), 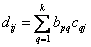 (3). Подставляя (3) в (2) получим:
(3). Подставляя (3) в (2) получим: 
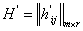
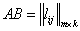 , тогда
, тогда 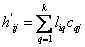 (4),
(4), 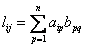 (5). Подставляя (5) в (4) получим:
(5). Подставляя (5) в (4) получим:
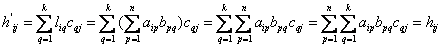
Вывод: Матрицы 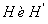 имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.
имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.
Умножение матриц дистрибутивно 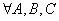 :
: 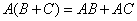
Доказательство:
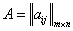 так как определено
так как определено 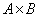 , то
, то 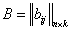 и определено
и определено 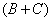 , то
, то 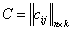
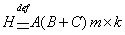 размерности
размерности
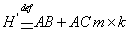 размерности
размерности
Матрицы 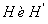 имеют одинаковую размерность, покажем расположение одинаковых элементов:
имеют одинаковую размерность, покажем расположение одинаковых элементов:
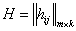 ,
, 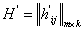
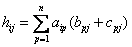 ,
, 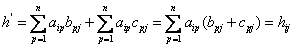
Вывод: На одинаковых местах расположены одинаковые элементы.
3. 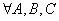 ,
, 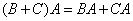 . Если определены
. Если определены 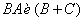 матрицы, то доказательство проводим аналогично свойству 2.
матрицы, то доказательство проводим аналогично свойству 2.
4. 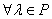 ,
, 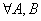 :
: 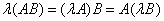 , если определена матрица
, если определена матрица 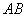
Доказательство:

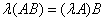 . Пусть
. Пусть 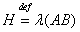 ,
, 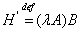
 ,
, 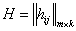 ,
, 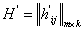
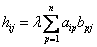
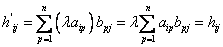
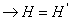
5. Умножение матриц в общем случае не коммутативно. Рассмотрим это на примере:
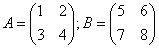 , тогда
, тогда 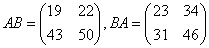
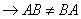
Вз3 Техника матричного умножения
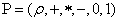 поле скаляров,
поле скаляров, 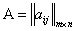 ,
, 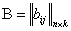
Свойства:
Произведение 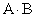 можно рассматривать, как результат умножения столбцов матрицы
можно рассматривать, как результат умножения столбцов матрицы 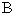 на
на  слева и как результат умножения строк матрицы
слева и как результат умножения строк матрицы  на
на 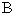 справа.
справа.
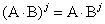
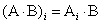
Пусть 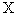 матрица
матрица 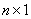 ,
, 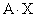 -линейная комбинация столбцов матрицы
-линейная комбинация столбцов матрицы  коэффициенты которой служат элементы матрицы
коэффициенты которой служат элементы матрицы 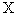
Пример
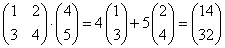
Пусть 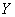 -матрица
-матрица 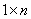 , тогда
, тогда 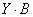 -линейная комбинация строк матрицы
-линейная комбинация строк матрицы 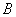 коэффициенты которой служат элементы матрицы
коэффициенты которой служат элементы матрицы 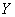
Пример:
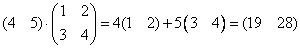
Столбцы матрицы 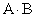 -линейная комбинация столбцов матрицы
-линейная комбинация столбцов матрицы  . Строки
. Строки 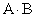 -линейная комбинация строк матрицы
-линейная комбинация строк матрицы 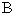 .
.
Вз4 Транспонирование произведения матриц
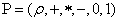 поле скаляров,
поле скаляров, 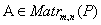 ,
, 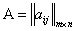 ,
, 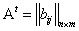 ,
, 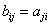
Теорема
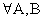 если
если 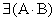 , то
, то 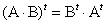 . Обозначим:
. Обозначим: 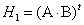 ,
, 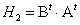
Доказательство:
 1) Пусть
1) Пусть 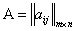 ,
, 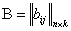
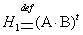 - размерности
- размерности 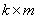 ,
,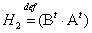 - размерности
- размерности 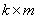 , тогда
, тогда 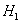 и
и 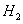 имеют одинаковую размерность
имеют одинаковую размерность
2)  ,
, 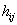 -элемента расположенный в
-элемента расположенный в 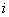 -строке,
-строке, 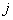 -столбце матрицы
-столбце матрицы 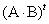 т.е
т.е 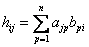
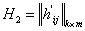 ,
, 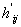 -произведение
-произведение 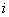 -строки транспонированной
-строки транспонированной 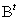 на
на 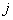 столбец
столбец 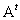 ,
, 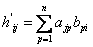
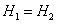
Глава III
Вз1 Обратимые матрицы
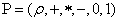 поле скаляров, множество
поле скаляров, множество 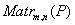 матриц порядка
матриц порядка 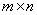
Определение. Квадратная матрица 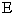 порядка
порядка 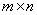 называется единичной матрицей
называется единичной матрицей 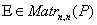 ,
, 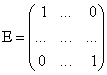
Пусть 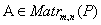 ,
, 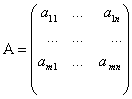
Теорема 1
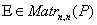 , то для
, то для 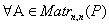 выполняется
выполняется 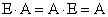
Доказательство:

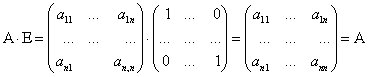
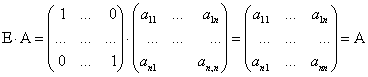
Из этого следует 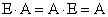 . Матрица
. Матрица 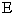 является единичной матрицей. Она выполняет роль единицы при умножении матриц.
является единичной матрицей. Она выполняет роль единицы при умножении матриц.
Определение. Квадратная матрица 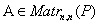 называется обратимой если существует
называется обратимой если существует 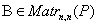 так, что выполняются условия
так, что выполняются условия 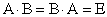
Матрица 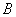 называется обратной к
называется обратной к 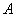 и обозначается
и обозначается 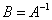 , тогда если
, тогда если 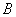 -это обратная к
-это обратная к 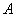 , то
, то 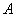 обратная к
обратная к 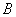
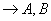 -это взаимообратные матрицы т.е.
-это взаимообратные матрицы т.е. 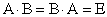
Теорема 2
Если 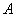 -обратима, то существует только одна матрица обратная к
-обратима, то существует только одна матрица обратная к 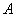
Доказательство:
 Пусть дана матрица
Пусть дана матрица 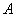 , которая обратима и пусть существуют матрицы
, которая обратима и пусть существуют матрицы 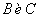 обратные к
обратные к 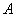 т.е.
т.е. 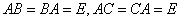 . Имеем
. Имеем 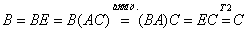
 "Инкарнация" кватернионов
"Инкарнация" кватернионов
*-Алгебры и их применение
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка