Структурный синтез устройств с мультидифференциальными операционными усилителями
Содержание
1. Постановка задачи
2. Принципы построения мультидифференциальных ОУ
3. Обобщенная структура и основные свойства электронных схем с мультидифференциальными ОУ
4. Собственная компенсация влияния частотных свойств мультидифференциальных ОУ
5. Звенья активных фильтров с мультидифференциальными ОУ
6. Мультидифференциальные ОУ в аналоговых интерфейсах и портах ввода
Выводы и рекомендации
Библиографический список
1. Постановка задачи
мультидифференциальный операционный усилитель аналоговый
Создание широкодиапазонных аналоговых устройств и IP блоков как с фиксированными, так и управляемыми параметрами связано либо с совершенствованием технологии производства активных компонентов, либо с построением низкочувствительных принципиальных схем, в рамках которых путем параметрической оптимизации удается в несколько раз (иногда на порядок) уменьшить влияние частоты единичного усиления (f1) этих компонентов на результирующие характеристики изделия. Указанные структуры и соответствующие им принципиальные схемы характеризуются собственной компенсацией влияния указанного параметра на чувствительность передаточной функции Ф(р).
В этом случае активная чувствительность электронной схемы будет иметь следующий вид:
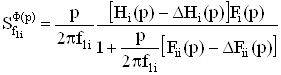 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
где 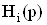 ВатАУ локальная передаточная функция идеализированной схемы при подаче сигнала на вход i-го активного элемента;
ВатАУ локальная передаточная функция идеализированной схемы при подаче сигнала на вход i-го активного элемента; 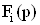 ВатАУ передаточная функция, реализуемая идеализированной схемой на выходе i-го активного компонента;
ВатАУ передаточная функция, реализуемая идеализированной схемой на выходе i-го активного компонента; 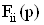 ВатАУ локальная передаточная функция идеализированной схемы на выходе i-го активного компонента при подаче сигнала в общем случае на его инвертирующий вход.
ВатАУ локальная передаточная функция идеализированной схемы на выходе i-го активного компонента при подаче сигнала в общем случае на его инвертирующий вход.
Указанные в соотношении (1) приращения локальных передаточ-ных функций 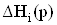 Ваи
Ваи 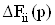 Вадостигаются благодаря введению в схему дополнительных (компенсирующих) обратных связей, связывающих диф-ференциальный вход i-го активного элемента с дополнительным входом (узлом) схемы. Такая связь является достаточной для создания разностных членов и единственной. Для сохранения неизменным набора идеализированных передаточных функций
Вадостигаются благодаря введению в схему дополнительных (компенсирующих) обратных связей, связывающих диф-ференциальный вход i-го активного элемента с дополнительным входом (узлом) схемы. Такая связь является достаточной для создания разностных членов и единственной. Для сохранения неизменным набора идеализированных передаточных функций 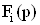 Ваи Ф(р) (все входящие в структуру активные элементы идеальны) необходимо обеспечить высокое по сравнению с другими резистивными элементами входное сопротивление четырехполюсника, обеспечивающего указанную дополнительную обратную связь.
Ваи Ф(р) (все входящие в структуру активные элементы идеальны) необходимо обеспечить высокое по сравнению с другими резистивными элементами входное сопротивление четырехполюсника, обеспечивающего указанную дополнительную обратную связь.
Ранее на многочисленных примерах показано, что успех применения принципа собственной компенсации связан со степенью свободы исходной схемы, которая определяется числом неиспользуемых (исходно заземленных) входов дифференциальных активных элементов. В большинстве случаев это не выполняется и приходится применять дополнительные операционные усилители (ОУ), решающие задачу согласования дифференциального входа i-го активного элемента и масштабирования сигнала для реализации необходимых параметрических условий собственной компенсации.
Анализ схемотехники современных ОУ показывает, что более 50 % потребляемых этими активными элементами тока приходится на выходной каскад, а попытки изменить это соотношение приводят к большому выходному сопротивлению ОУ и, следовательно, в целом ряде случаев тАУ к ухудшению многих качественных показателей функциональных устройств. Например, в активных фильтрах гарантированное затухание в области верхних частот непосредственно определяется соотношением выходного сопротивления и сопротивления частотно-задающих цепей.
Одним из выходов из сложившегося положения является создание для современной аналоговой микросхемотехники мультидифференциальных ОУ (МОУ) тАУ операционных усилителей, имеющих несколько инвертирующих и неинвертирующих входов, создающих необходимое для принципа собственной компенсации число степеней свободы практически без увеличения потребляемой мощности.
2. Принципы построения мультидифференциальных ОУ
Для построения указанного типа активных элементов достаточно изменить структуру входного дифференциального каскада (рис. 1), при этом такая модификация не должна существенно влиять на коэффициент ослабления синфазного сигнала [8].
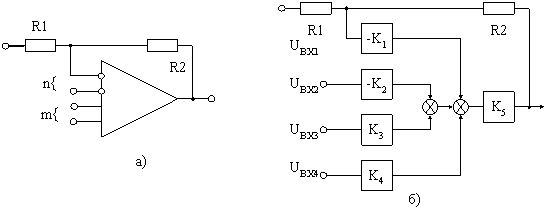
Рис. 1 Функциональная (а) и структурная (б) схемы
многовходового ОУ
В частности, такой ОУ может иметь равноправных инвертирующих и m равноправных неинвертирующих входов. На один из инвертирующих входов включается цепь отрицательной обратной связи (ООС), задающая масштабный коэффициент усиления. Коэффициент передачи по каждому из входов при охватывании такого усилителя цепью ООС можно найти из следующих выражений (при условии, что остальные входы заземлены и KiK5 >>1):
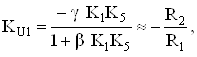 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
где 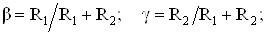
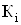 тАУ коэффициент передачи по напряжению соответствующего каскада ОУ;
тАУ коэффициент передачи по напряжению соответствующего каскада ОУ;
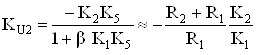 ; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (3)
; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа (3)
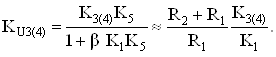 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(4)
Из выражений (2)тАУ(4) следует, что если коэффициенты передачи К1 ÷ К4 равны между собой по абсолютной величине, то результирующий коэффициент усиления по напряжению для такого многовходового ОУ, охваченного цепью ООС, совпадает с классическим для типового инвертирующего и неинвертирующего включений, а коэффициент передачи для дополнительного инвертирующего входа отличается от неинвертирующего только знаком.
Вариант построения схемы ОУ, соответствующего структурной схеме рис. 1, приведен на рис. 2.
Если считать, что коэффициент передачи повторителя тока на транзисторах VT5, VT6 равен единице, то коэффициенты передачи по напряжению К1 - К4 и К2- К4 попарно равны и определяются следующим образом:
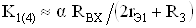 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
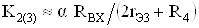 , ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(6)
, ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(6)
где RВХ тАУ входное сопротивление промежуточного усилителя на транзи-сторах VT7, VT8; rЭi тАУ дифференциальное сопротивление перехода база-эмиттер транзистора соответствующей дифференциальной пары; 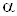 ВатАУ ко-эффициент передачи тока базы соответствующего транзистора дифферен-циальной пары.
ВатАУ ко-эффициент передачи тока базы соответствующего транзистора дифферен-циальной пары.
Сопротивления резисторов R3, R4 можно выбирать одинаковыми или различными; если отношение сопротивлений не равно единице, появляется дополнительная возможность масштабирования коэффициентов усиления по входам 2 и 3. Однако такое дополнительное масштабирование определенным образом влияет на частотную характеристику усилителя. Действительно, если считать, что коэффициенты передачи К1 и К5 соответствующих каскадов усиления ОУ описываются передаточными функциями первого порядка, а влиянием частотной зависимости a можно пренебречь, то для входа 1 коэффициент передачи ОУ, охваченного цепью ООС, можно представить как

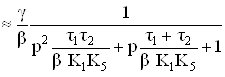 , (7)
, (7)
где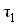 ВатАУ постоянная времени дифференциального каскада;
ВатАУ постоянная времени дифференциального каскада; 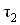 ВатАУ постоянная времени промежуточного каскада;
ВатАУ постоянная времени промежуточного каскада; 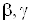 ВатАУ соответствующие коэффициенты передачи цепи обратной связи, имеющие тот же смысл, что и в (2).
ВатАУ соответствующие коэффициенты передачи цепи обратной связи, имеющие тот же смысл, что и в (2).

Рис. 2. Упрощенная принципиальная схема
мультидифференциального ОУ
При подаче входного сигнала на вход 2 (база транзистора VT3, рис. 2), при условии, что постоянные времени каналов К2 и К1 идентичны, по аналогии с (7) можно записать:
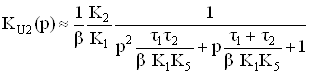 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)
Из сопоставления выражений (7) и (8) следует, что они, по сути, идентичны при выполнении условия К2 = К1. При попытке увеличить коэффициент усиления за счет уменьшения глубины обратной связи эквивалентная постоянная времени также увеличивается, так как коэффициент 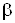 входит в знаменатель выражений (7) и (8), что приводит к уменьшению частоты среза, то есть спад частотной характеристики замкнутого и разомкнутого усилителей практически совпадает.
входит в знаменатель выражений (7) и (8), что приводит к уменьшению частоты среза, то есть спад частотной характеристики замкнутого и разомкнутого усилителей практически совпадает.
Иная ситуация возникает при выполнении условия К2 > К1. В этом случае эквивалентная постоянная времени определяется петлевым усилением, частота среза остается неизменной, а частота единичного усиления возрастает. То есть возрастает площадь усиления ОУ, охваченного цепью ООС. Эта ситуация подтверждается результатами моделирования (рис. 3) схемы, приведенной на рис. 2. По стандартному инвертирующему включению КU1=1, а при R3 = 2R4 коэффициент передачи К2 В» 2К1 с точностью до конечного сопротивления rЭ (см. (5)тАУ(6)).
Графики, приведенные на рис. 3, показывают, что частота единичного усиления при подаче сигнала на вход 2 (или 3) возрастает примерно в два раза, что определяется принятым соотношением К2 В» 2К1. Естественно, такое расширение полосы возможно лишь при определенной коррекции частотной характеристики усилителя: коррекция ОУ осуществляется конденсатором СК (рис. 2) так, чтобы его передаточная функция соответствовала апериодическому звену второго порядка и постоянная времени промежуточного каскада была много меньше постоянной времени входного каскада.
Точностные характеристики такого ОУ (в частности, напряжение смещения, приведенное ко входу) хуже, чем у обычного, т.к. ошибки, возникающие в каждом дифференциальном каскаде, в общем случае складываются. В ОУ может быть предусмотрена балансировка напряжения смещения, например, за счет изменения коэффициента передачи повторителя тока на транзисторах VT5, VT6.
Динамический диапазон многовходового ОУ определятся, с одной стороны, динамическим диапазоном активной работы каждого дифференциального каскада, с другой тАУ максимальным выходным напряжением, поскольку такой каскад осуществляет суммирование входных сигналов. Поэтому должно выполняться следующее условие:
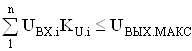 .
.
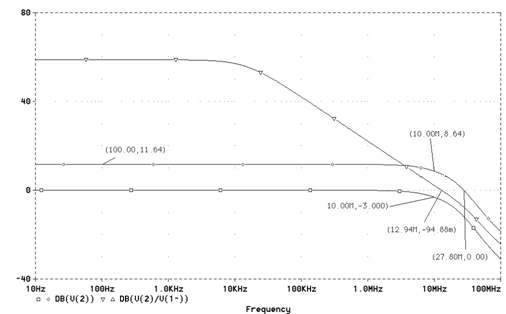
Рис. 3. Амплитудно-частотные характеристики
многовходового ОУ при подаче сигнала на вход 1 (□),
вход 2 (◊) и разомкнутого усилителя (Ñ)
Другой вариант построения многовходового ОУ приведен на рис. 4а), а функциональная схема, ему соответствующая, тАУ на рис. 4б). На рис. 4в приведена функциональная схема, к которой может быть преобразован ОУ, если поменять местами точки подключения коллектора транзистора VT4 и объединенных коллекторов транзисторов VT1 тАУ VT3.
С учетом того, что ток эмиттера транзистора VT4 в три раза больше токов эмиттеров каждого из транзисторов VT1тАУVT3, а также в предположении, что коэффициент передачи повторителя тока на транзисторах VT5тАУVT6 близок к единице, по инвертирующим входам коэффициент передачи входного каскада составит:

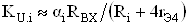 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)
где RВХтАУ входное сопротивление промежуточного каскада на транзисторе VT6; Ri тАУ сопротивление резистора R1тАУR3; rЭ4 тАУ дифференциальное сопротивление эмиттера транзистора VT4.
Для неинвертирующего входа, при условии, что сопротивления резисторов R1тАУR3 равны, коэффициент усиления можно записать как
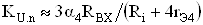 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (10)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (10)
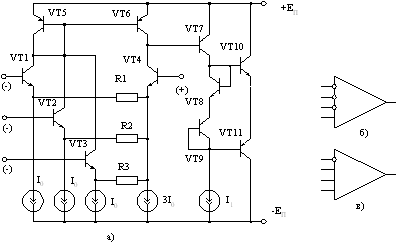
Рис. 4. Упрощенная принципиальная схема мультидифференциального каскада (а) и возможные варианты его функциональных схем (б), (в)
Следовательно, по аналогии с выражением (7) для стандартного инвертирующего включения ОУ (при остальных заземленных входах) можно записать
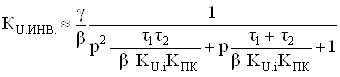 ,
,
где КПК тАУ коэффициент усиления промежуточного каскада.
По аналогии с (8) для коэффициента усиления по любому из неинвертирующих входов, на который не подана обратная связь, можно записать
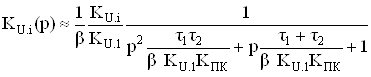 .
.
По неинвертирующему входу для рассматриваемого случая

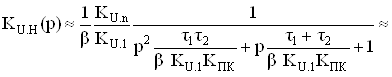

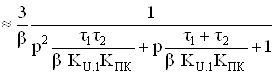 .
.
Следует отметить, что напряжение смещения, приведенное ко входу у усилителя, представленного на рис. 4а, практически совпадает с аналогичным параметром обычного ОУ с одиночным дифференциальным каскадом на входе, но при условии, что плотность токов эмиттеров транзисторов VT1тАУVT4 одинакова. Это достигается тем, что площадь эмиттера транзистора VT4 должна быть в три раза больше площади эмиттера транзисторов VT1тАУVT3. Как и в предыдущем случае, балансировку нуля по выходу ОУ можно осуществить изменением коэффициента передачи повторителя тока на транзисторах VT5тАУVT6.
При функциональном построении мультидифференциального ОУ по схеме рис. 4в коэффициент усиления при стандартном инвертирующем включении на низких частотах будет определяться по аналогии с выражением (2), а для неинвертирующего включения 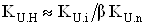 , то есть в три раза меньше, чем для случая функциональной схемы рис. 4б.
, то есть в три раза меньше, чем для случая функциональной схемы рис. 4б.
Естественно, частота единичного усиления в этом случае также уменьшается в три раза по сравнению с частотой единичного усиления разомкнутого усилителя.
При введении нескольких контуров ООС в МОУ происходит взаимное влияние цепей обратной связи на результирующий коэффициент передачи. При включении ОУ инвертирующего усилителя по обеим входам выражения для коэффициентов передачи по каждому входу в области низких частот будут выглядеть следующим образом:
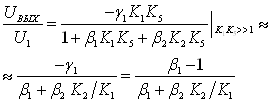 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(11)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(11)
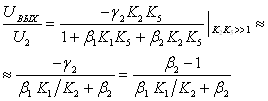 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(12)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(12)
где 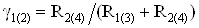 ;
; 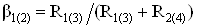 ; Ki тАУ коэффициент передачи соответствующего плеча дифференциального каскада (рис. 1б).
; Ki тАУ коэффициент передачи соответствующего плеча дифференциального каскада (рис. 1б).
При условии, что все Ki равны по абсолютной величине, что легко выполнимо, выражения (11) и (12) можно представить как
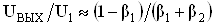 ; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(13)
; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(13)
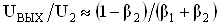 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (14)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (14)
Для неинвертирующего включения мультидифференциального ОУ по каждому из неинвертирующих входов коэффициент передачи можно представить как
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(15)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(15)
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(16)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(16)
Из выражений (11)тАУ(16) следует, что при использовании многоконтурных ООС глубина обратной связи возрастает, в частности, в классическом ОУ для неинвертирующего включения при 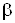 Ва= 0,5 коэффициент усиления будет близок к двум, а в рассматриваемом случае при
Ва= 0,5 коэффициент усиления будет близок к двум, а в рассматриваемом случае при 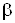 1 =
1 = 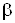 2 = = 0,5 коэффициент усиления будет близок к единице.
2 = = 0,5 коэффициент усиления будет близок к единице.
Очевидно, что при одновременном использовании инвертирующих и неинвертирующих входов выходное напряжение ОУ можно определить согласно принципу суперпозиции, если сопротивление источников сигналов будет много меньше входных сопротивлений соответствующих входов.
Поскольку коэффициенты КiтАУ комплексные и, в общем случае, постоянные времени высоких частот каждого дифференциального каскада различны, передаточная функция для случая неинвертирующего включения ОУ будет иметь вид:
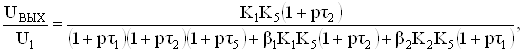 Ва(17)
Ва(17)
поэтому обеспечение устойчивости такого усилителя может оказаться сложной, но решаемой задачей.
Ток потребления стандартного ОУ складывается из следующих составляющих (если входной одиночный дифференциальный каскад выполнен аналогично рис. 2):
IОУ = IВК + I1 + 2I0 В» 2I1 + 2I0, ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(18)
где IВК, I1, 2I0тАУ токи, потребляемые выходным, промежуточным и входным дифференциальным каскадами.
Для схем мультидифференциальных ОУ, представленных на рис. 2 и 4 соответственно
IОУ = IВК + 2I1 + 4I0,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (19)
IОУ = IВК + 2I1 + 6I0,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (20)
откуда следует, что ток МОУ возрастает весьма незначительно по сравнению с классическим.
3. Обобщенная структура и основные свойства электронных схем с мультидифференциальными ОУ
Увеличение числа входов дифференциальных каскадов, как это было показано ранее, приводит к снижению коэффициента ослабления синфазного сигнала, причем он может зависеть от требуемого количества входов. Кроме этого, необходим поиск особенностей функционально-топологиче-ских принципов введения в схему дополнительных (компенсирующих) обратных связей и, следовательно, анализ основных свойств электронных схем с МОУ.
Для решения поставленной задачи воспользуемся обобщенной структурой электронных схем с МОУ (рис. 5).
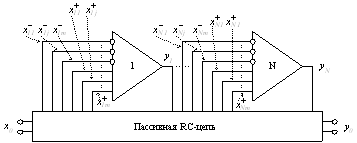
Рис. 5. Обобщенная структура с мультидифференциальными ОУ
Из векторного сигнального графа (рис. 6) этой структуры следует система векторно-матричных уравнений:
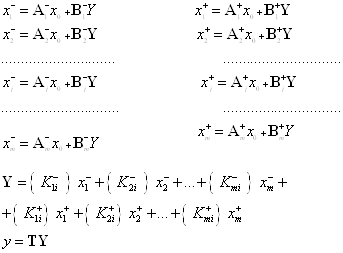 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(21)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(21)
Смысл векторов 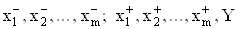 Васледует из рис. 6. Векторы
Васледует из рис. 6. Векторы 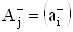 ,
, 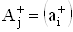 Варазмерностью N´1 описывают расщепитель входного сигнала x0 и связывают его с инвертирующим (-) и неинвертирующим (+) входами
Варазмерностью N´1 описывают расщепитель входного сигнала x0 и связывают его с инвертирующим (-) и неинвертирующим (+) входами 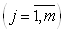 Вамультидифференциальных ОУ
Вамультидифференциальных ОУ 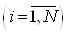 . Матрицы
. Матрицы 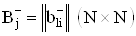 ,
, 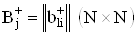 Ваобразованы локальными пе-редаточными функциями пассивной подсхемы, обеспечивающей передачу и преобразование сигнала со входа i-го активного элемента на j-й инвертирующий или неинвертирующий входы l-го МОУ. Активные элементы описываются диагональными матрицами размера (N´N):
Ваобразованы локальными пе-редаточными функциями пассивной подсхемы, обеспечивающей передачу и преобразование сигнала со входа i-го активного элемента на j-й инвертирующий или неинвертирующий входы l-го МОУ. Активные элементы описываются диагональными матрицами размера (N´N):
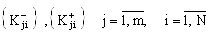 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (22)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (22)
компоненты которых являются передаточными функциями i-го МОУ по j-му инвертирующему (-) и неинвертирующему (+) входам.
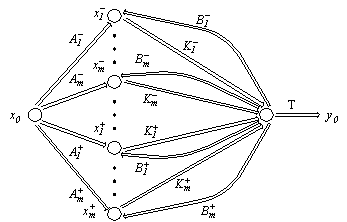
Рис. 6. Векторный сигнальный граф обобщенной структуры
Связь выходов активных элементов с нагрузкой осуществляется через сумматор, локальные передачи которого образуют вектор T = [ti] размера (N´1). Для учета влияния ослабления синфазного сигнала по различным входам введем в общем случае функции:
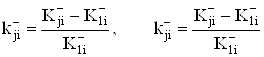 , ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (23)
, ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (23)
характеризующих неидентичность каналов усиления входного сигнала. Тогда
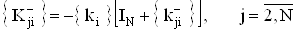 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(24)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(24)
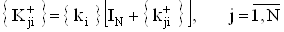 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(25)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(25)
Решение системы (21) приводит к следующему вектору выходных сигналов МОУ:
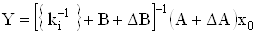 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (26)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (26)
где 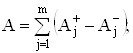 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа Ва(27)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВа Ва(27)
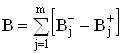 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (28)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (28)
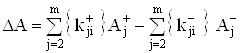 Ва;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (29)
Ва;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (29)
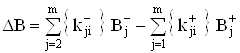 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (30)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (30)
Из (26) может быть получена передаточная функция любого электронного устройства с МОУ:
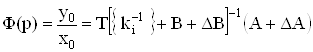 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (31)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (31)
Реально коэффициенты ослабления синфазного сигнала достаточно велики, поэтому при анализе их влияния на функцию (31) можно исключить мультипликативные составляющие, представляющие собой величины второго порядка малости.
Рассмотрим влияние j-го коэффициента для инвертирующего входа i-го активного элемента. Индекс j соответствует номеру матрицы:
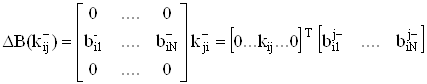 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (32)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (32)
Тогда по методу Дуайра и У0 [2] (метода пополнения при обращении матрицы) получим:
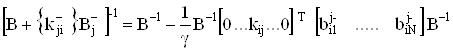 , (33)
, (33)
где 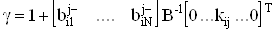 .
.
Следовательно,
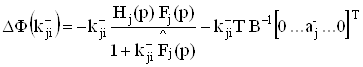 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (34)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (34)
В выражении (34)
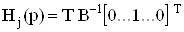 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (35)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (35)
является локальной передаточной функцией системы при подаче сигнала на j-й вход i-го активного элемента, представляет собой передаточную функцию при условии, что вектор Т образован компонентами i-й строки матрицы 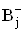 , а
, а
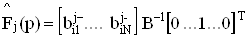 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (36)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (36)
является передаточной функцией системы при подаче сигнала на j-й вход i-го МОУ при условии, что вектор Т образован указанным выше способом.
Аналогичный результат получается и для 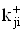 . Однако, как это следует из (27) и (28), в соответствующих выражениях необходимо изменить знак слагаемых. С учетом структуры вектора (28) полное приращение передаточной функции системы будет иметь следующий вид
. Однако, как это следует из (27) и (28), в соответствующих выражениях необходимо изменить знак слагаемых. С учетом структуры вектора (28) полное приращение передаточной функции системы будет иметь следующий вид
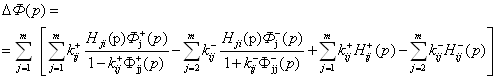 ВаВаВа Ва(37)
ВаВаВа Ва(37)
Здесь и далее
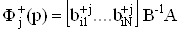 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (38)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (38)
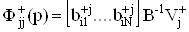 ; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(39)
; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(39)
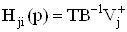 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (40)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (40)
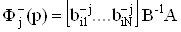 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (41)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (41)
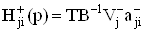 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (42)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (42)
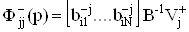 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВа Ва(43)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВа Ва(43)
где 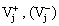 ВатАУ вектор-столбец размером (N ´ 1), имеющий отличную от нуля и равную единице компоненту, соответствующую j-му неинвертирующему (инвертирующему) входу i-го МОУ (см. структуру вектора (30);
ВатАУ вектор-столбец размером (N ´ 1), имеющий отличную от нуля и равную единице компоненту, соответствующую j-му неинвертирующему (инвертирующему) входу i-го МОУ (см. структуру вектора (30); 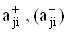 ВатАУ передачи пассивной подсхемы от источника сигнала к j-му неинвертирующему (инвертирующему) входу i-го усилителя;
ВатАУ передачи пассивной подсхемы от источника сигнала к j-му неинвертирующему (инвертирующему) входу i-го усилителя;  тАУ коэффициент ослабления синфазного сигнала i-го МОУ по j-му неинверти-рующему входу;
тАУ коэффициент ослабления синфазного сигнала i-го МОУ по j-му неинверти-рующему входу;  тАУ коэффициент относительной неидеальности i-го МОУ j-му инвертирующему входу (см. (23)).
тАУ коэффициент относительной неидеальности i-го МОУ j-му инвертирующему входу (см. (23)).
В соотношениях (37)тАУ(43) индекс j характеризует номер матрицы, входящей в ряд (29).
Структура приращения передаточной функции (37) указывает на возможность взаимной компенсации влияния неидентичности каналов мультидифференциальных ОУ. Кроме этого, последние две составляющие ряда (37) могут быть направлены на компенсацию влияния выходного сопротивления применяемых активных элементов на амплитудно-частот-ные характеристики фильтров.
Примененный метод пополнения при обращении матрицы можно использовать и при анализе влияния площади усиления МОУ. Из соотношения (31) следует приращение передаточной функции, вызванное влиянием площади усиления (Пi) МОУ:
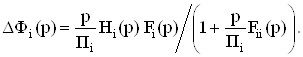 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(44)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(44)
Здесь
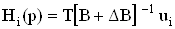 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(45)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(45)
является передаточной функцией идеализированной обобщенной схемы модели при подключении источника сигнала к одному из неинвертирующих входов i-го МОУ;
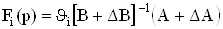 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(46)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(46)
есть передаточная функция на выходе i-го МОУ, а
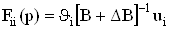 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(47)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(47)
тАУ аналогичная функция при условии подключения источника входного сигнала к его неинвертирующему входу.
В приведенных соотношениях векторы  Ваимеют только одну единицу на позиции, соответствующей номеру i-го усилителя. Другие их компоненты равны нулю. Таким образом,
Ваимеют только одну единицу на позиции, соответствующей номеру i-го усилителя. Другие их компоненты равны нулю. Таким образом,
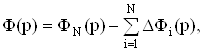 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(48)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(48)
Дифференцированием можно определить активную чувстви-тельность модели
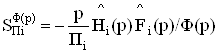 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (49)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (49)
где локальные передаточные функции 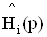 ,
, 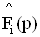 Ваопределяются аналогично с учетом влияния частотных свойств активных элементов структуры.
Ваопределяются аналогично с учетом влияния частотных свойств активных элементов структуры.
 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (50)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (50)
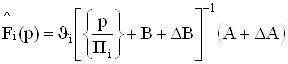 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (51)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (51)
Приведенные соотношения устанавливают связь активной составляющей чувствительности схемы с границами ее динамического диапазона. Действительно, спектральная плотность мощности шума на выходе цепи определяется как
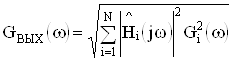 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (52)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (52)
где 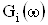 ВатАУ эквивалентная спектральная плотность, приведенная ко входу i-го МОУ, а максимальный уровень выходного напряжения
ВатАУ эквивалентная спектральная плотность, приведенная ко входу i-го МОУ, а максимальный уровень выходного напряжения
 ;
;
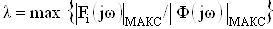 Ва,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (53)
Ва,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (53)
при условии, что 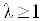 . В противном случае
. В противном случае 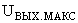 Ваи максимальное выходное напряжение
Ваи максимальное выходное напряжение 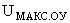 Ваактивных элементов совпадают. Таким образом, уменьшение модуля активной составляющей чувствительности и расширение диапазона рабочих частот схемы за счет уменьшения модуля локальной функции (51) приводит к ВлперенапряжениюВ», которое и уменьшает максимальный уровень выходного сигнала. Следовательно, единственным способом расширения диапазона рабочих частот и динамического диапазона схемы является уменьшение модуля локальной функции (50) при сохранении неизменными функций (51) и
Ваактивных элементов совпадают. Таким образом, уменьшение модуля активной составляющей чувствительности и расширение диапазона рабочих частот схемы за счет уменьшения модуля локальной функции (51) приводит к ВлперенапряжениюВ», которое и уменьшает максимальный уровень выходного сигнала. Следовательно, единственным способом расширения диапазона рабочих частот и динамического диапазона схемы является уменьшение модуля локальной функции (50) при сохранении неизменными функций (51) и  .
.
4. Собственная компенсация влияния частотных свойств мультидифференциальных ОУ
Соотношение (44) с учетом структуры идеализированной передаточной функции
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (54)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (54)
можно интерпретировать сигнальным графом, изображенным на рис. 7. С учетом выражений (54), (44), (46) и (47) можно получить векторный сигнальный граф (рис. 8) системы с учетом влияния i-го МОУ. Наличие узла
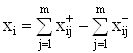 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (55)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (55)
не изменяет структуру и смысл локальной функции, т.к. любую компоненту вектора  Ваможно рассматривать как равную единице разность передач пассивной части цепи на инвертирующий и неинвертирующий входы.
Ваможно рассматривать как равную единице разность передач пассивной части цепи на инвертирующий и неинвертирующий входы.
Из рассмотрения векторного сигнального графа следует важный в теоретическом отношении вывод: изменение локальных передаточных функций 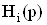 Ваи
Ваи 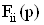 Вапри фиксированной передаточной функции возможно тогда и только тогда, когда дифференциальный вход xi i-го МОУ связан с дополнительным входом схемы.
Вапри фиксированной передаточной функции возможно тогда и только тогда, когда дифференциальный вход xi i-го МОУ связан с дополнительным входом схемы.
Для доказательства этого утверждения введем вектор
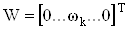 ,
, 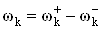 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (56)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (56)
В этом случае рассматриваемая структура будет описываться следующей системой уравнений:
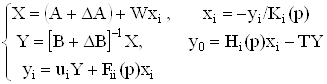 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(57)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(57)
где 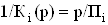 .
.
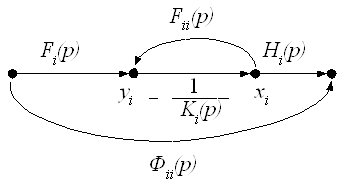
Рис. 7. Сигнальный граф электронной схемы при влиянии i-го МОУ
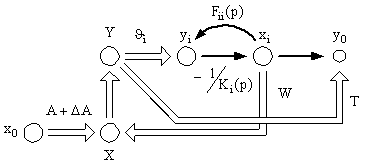
Рис. 8. Векторный сигнальный граф электронной системы
при влиянии i-го входа МОУ
Решение системы уравнений (57) приводит к следующему результату:
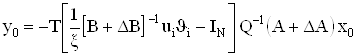 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (58)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (58)
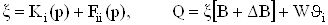 .
.
При обращении матрицы  воспользуемся методом пополнения:
воспользуемся методом пополнения:
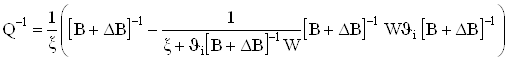 . (59)
. (59)
Следовательно, передаточная функция структуры
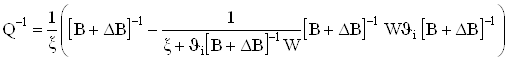 , (60)
, (60)
где 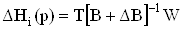 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (61)
;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (61)
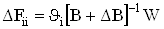 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (62)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (62)
Таким образом, введение вектора W обеспечивает изменение только локальных функций 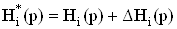 Ваи
Ваи 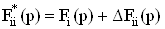 , со-храняя при этом неизменными передаточную функцию идеализированной системы Фu(p) и передаточную функцию на выходе i-го активного элемента Fi(p). Изменение знака в (61) и (62), как это видно из (56), достигается за счет дифференциальных свойств активных элементов схемы.
, со-храняя при этом неизменными передаточную функцию идеализированной системы Фu(p) и передаточную функцию на выходе i-го активного элемента Fi(p). Изменение знака в (61) и (62), как это видно из (56), достигается за счет дифференциальных свойств активных элементов схемы.
Полученный результат имеет достаточно простую физическую трактовку. При идеальном активном элементе (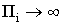 ) дифференциальный входной сигнал xi не зависит от частоты, а при бесконечном статическом коэффициенте усиления этот сигнал равен нулю и дополнительный контур обратной связи прекращает свое действие, что в конечном счете и сохраняет неизменным не только идеализированную передаточную функцию, но и локальную функцию Fi(p). Таким образом, получение топологических условий собственной компенсации является достаточным.
) дифференциальный входной сигнал xi не зависит от частоты, а при бесконечном статическом коэффициенте усиления этот сигнал равен нулю и дополнительный контур обратной связи прекращает свое действие, что в конечном счете и сохраняет неизменным не только идеализированную передаточную функцию, но и локальную функцию Fi(p). Таким образом, получение топологических условий собственной компенсации является достаточным.
Покажем их единственность. Из соотношений (46) и (57) следует, что для сохранения функций Фu(p) и Fi(p) необходимо сохранить не только матрицы В и DВ, но и набор векторов Т, А, DА,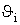 . Единственная незафиксированная составляющая набора предложенных функций ui связывает вход i-го активного элемента источником x. Действительно,
. Единственная незафиксированная составляющая набора предложенных функций ui связывает вход i-го активного элемента источником x. Действительно,
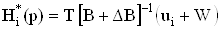 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (63)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (63)
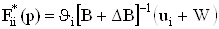 .
.
Этот вывод подтверждается и рассмотрением векторного сигнального графа (рис. 8). Создание параллельного пути передачи от узла xi к выходу схемы возможно только его соединением с дополнительным входом схемы и, следовательно, как это видно из (21), со входами активных элементов. Таким образом, сформулированное условие является единственным.
Ответ на вопрос об уровне компенсации в общем случае остается открытым, так как зависит от структуры матрицы [В + DВ] и вектора W. Из (63) видно, что в общем случае полную компенсацию обеспечить невозможно в силу неосуществимости условия
 . ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (64)
. ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (64)
В этой связи применение настоящего результата при решении практических задач связано с анализом структуры поправочных полиномов электронных схем различного функционального назначения.
5. Звенья активных фильтров с мультидифференциальными ОУ
При построении активного интерфейса современных систем радиоэлектронного назначения особое место занимают активные фильтры, обеспечивающие предварительную частотную селекцию сигналов сенсорных элементов. Именно точность реализации необходимых частотных характеристик и динамический диапазон этих устройств непосредственно определяют основные качественные показатели многих микрокомпьютерных систем автоматического управления и технической диагностики. В основе построения как многопетлевых, так и каскадных фильтров лежат звенья, реализующие передаточную функцию второго порядка. Использование принципа собственной компенсации влияния площади усиления дифференциальных ОУ практически всегда связано с увеличением в схеме их числа и, следовательно, к увеличению потребляемой мощности [9]. Покажем эффективность использования в их структуре мультидифференциальных ОУ.
В общем случае звено второго порядка должно реализовать следующую передаточную функцию:
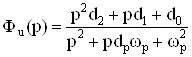 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (65)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (65)
где 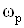 и
и 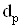 ВатАУ соответственно частота и затухание полюса.
ВатАУ соответственно частота и затухание полюса.
Влияние площади усиления ОУ приводит к приращению знаменателя этой функции на следующий полином:
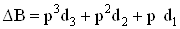 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (66)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (66)
где 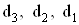 ВатАУ коэффициенты, обратно пропорциональные площади усиления ОУ.
ВатАУ коэффициенты, обратно пропорциональные площади усиления ОУ.
Именно поэтому в рабочем диапазоне частот это приводит к изменению как затухания, так и частоты полюса звена:
 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (67)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (67)
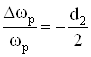 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(68)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(68)
Приведенные соотношения показывают, что относительное изменение затухания полюса пропорционально реализуемой добротности  Ваи для высокоселективных устройств может достигать больших значений, включая и потерю устойчивости. В то же время, как это хорошо известно из теории фильтров, отклонение частоты полюса от желаемого значения в
Ваи для высокоселективных устройств может достигать больших значений, включая и потерю устойчивости. В то же время, как это хорошо известно из теории фильтров, отклонение частоты полюса от желаемого значения в 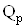 раз сильнее влияет на изменение реализуемых частотных характеристик. Именно поэтому обеспечение высоких качественных показателей связано со стабилизацией как затухания, так и частоты полюса звеньев второго порядка.
раз сильнее влияет на изменение реализуемых частотных характеристик. Именно поэтому обеспечение высоких качественных показателей связано со стабилизацией как затухания, так и частоты полюса звеньев второго порядка.
Рассмотрим основные подходы к решению этой задачи. Из (47) и (62) видно, что в рамках принципа собственной компенсации относительные изменения полинома
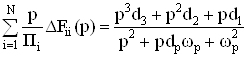 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (69)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (69)
должны компенсироваться введением дополнительных связей, образующих следующее приращение
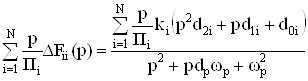 Ва.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (70)
Ва.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (70)
Тогда
 , ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (71)
, ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (71)
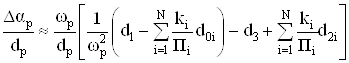 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (72)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (72)
Соотношения (71) и (72) показывают, что выбором 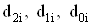 Ваи знаков ki можно обеспечить любой уровень собственной и взаимной компенсаций влияния площади усиления активных элементов на частоту и затухание полюса. Вытекающие из этих выражений функциональные признаки приведены в табл. 1.
Ваи знаков ki можно обеспечить любой уровень собственной и взаимной компенсаций влияния площади усиления активных элементов на частоту и затухание полюса. Вытекающие из этих выражений функциональные признаки приведены в табл. 1.
Приведенные результаты показывают, что в случае реализации на выходе i-го ОУ передаточной функции
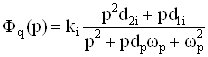 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (73)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (73)
возможна одновременная компенсация изменений частоты и затухания полюса. Однако в этом случае дополнительная обратная связь характеризуется положительным возвратным соотношением, что при большой добротности полюса может существенно уменьшить запас устойчивости. Именно поэтому первый вариант компенсации изменения затухания полюса (табл. 1) более предпочтителен [5].
Рассмотрим применение полученных результатов для построения схемы звена второго порядка с собственной и взаимной компенсацией. На рис. 9 пр
Вместе с этим смотрят:
GPS-навигация
IP-телефония. Особенности цифровой офисной связи
РЖсторiя диктофону
РЖсторiя звтАЩязку та його розвиток
Автоматизация электротельфера