Системи масового обслуговування з очiкуванням без обмеження на довжину черги

Системи масового обслуговування з очiкуваннямбез обмеження на довжину черги

1. Системи масового обслуговування з очiкуванням

Багатоканальнi СМО з обмеженою чергою. Нехай i система СМО, що маi Ваканалiв. Кожна заявка надходить до СМО, починаi обслуговуватись, коли хоча б один iз каналiв вiльний. Якщо усi канали зайнятi, тодi заявка потрапляi у накопичувач, де чекаi звiльнення хоча б одного iз каналiв. Нехай черга у накопичувачi обмежена числом . Якщо, один iз каналiв звiльняiться, заявка надходить на обслуговування до звiльненого каналу по черзi, з якою заявка надiйшла у СМО. Якщо заявка застане усi канали i усi мiсця у накопичувачi зайнятими, то вона втрачаiться. Потiм припускатимемо, що вхiдний потiк заявок також пуассонiвського з параметром , а потiк обслугованих заявок також пуассонiвський с параметром . Тодi система може знаходитись у станах ВаПричому ВатАУ це стани, коли немаi черги, тобто вiдповiдно ВатАУ всi канали вiльнi, ВатАУ один зайнятий, тАж , ВатАУ усi Ваканалiв зайнятi, Ва- усi канали зайнятi i одна заявка в черзi, тАж , ВатАУ стан, коли всi Ваканалiв i всi Вамiсць у накопичувачi зайнятi, тобто заявка, що надходить в такий момент втрачаiться. Можна графiчно на рис. (1) стрiлками вказати усi переходи вiд стану до стану, а над стрiлками ймовiрностi переходiв за час , якщо Вамалий.

Рисунок 1

Якщо порiвняти СМО з вiдмовами i СМО з обмеженою чергою, то зрозумiло, що для ймовiрностей переходу , коли , ми одержуiмо такi ж диференцiальнi рiвняння як i рiвняння системи без черги.

Отже потрiбно скласти рiвняння для перехiдних ймовiрностей, коли .

Нехай . Враховуючи властивостi простiших потокiв i формулу Смолуховського-Чепмена

,(1)

де ВатАУ функцiя що задовольняi умовi .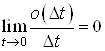

, (2)

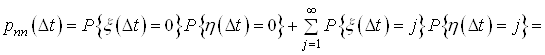
, (3)

де як i ранiше Вачисло заявок, що надходять до СМО за час ,
а ВатАУ число заявок, що обслугованi за час .

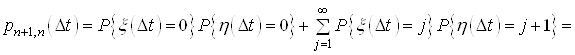
Ва(4)

Тепер врахуiмо (2), (3 i (4) до (1)

Вiднiмемо вiд обох частин останньоi рiвностi Вата роздiлимо на

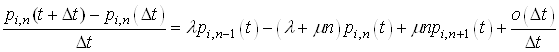
Перейдемо до границi в обох частинах, коли

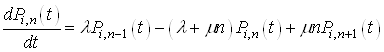(5)

Тепер, продовжуючи аналогiчнi мiркування, можна одержати рiвняння для обчислення перехiдних ймовiрностей iз стану до стану, коли , де

Враховуючи формулу Смолуховського-Чепмена, а також властивостi простiшого (пуассонiвського) потоку можна записати:

Ва(6)

Далi за властивiстю стацiонарностi i ординарностi, маiмо:

, (7)

, (8)

. (9)

Врахуiмо (7), (8) i (9) до (6).

В останнiй рiвностi вiднiмемо вiд обох частин Ваi роздiлимо на .

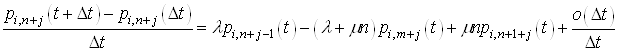
А тепер перейдемо до границi в обох частинах, коли , тодi

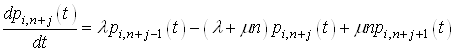(10)

де .

Останнi рiвняння системи, для визначення перехiдних ймовiрностей , мiстить :

Враховуючи тi ж самi властивостi стацiонарностi i ординарностi простiших (пуассонiвських) потокiв, одержимо:

, (11)

.Ва (12)

Якщо пiдставити (11) i (12) у рiвнiсть (10), тодi матимемо:

.

Якщо вiдняти вiд обох частин останньоi рiвностi , а далi роздiлити на , тодi запишемо

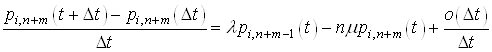
Тепер обчислимо границi вiд обох частин, якщо :

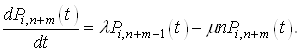(13)

Таким чином отримуiмо систему диференцiальних рiвнянь для обчислення ВатАУ ймовiрностей переходу вiд стану Вадо стану ВаСМО з чергою, що маi скiнченне число мiсць в накопичувачi:

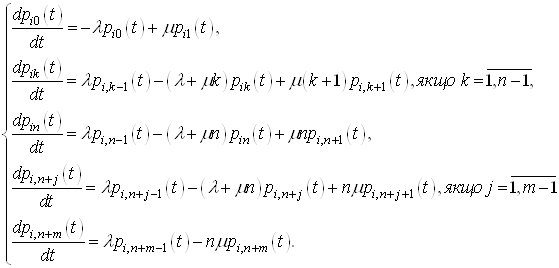(14)

Якщо спостерiгати СМО достатньо довгий час , тодi розвтАЩязок системи (14) можна знайти, якщо позначити Ва(фiнальнi ймовiрностi) у виглядi:

Ва(15)

Система (15) i лiнiйною, однорiдною, алгебраiчною системою з невiдомими . Для того, щоб знайти iдиний розвтАЩязок системи (15) необхiдно додати умову

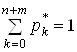.(16)

Ранiше було доведено, що для усiх Вадii формула:

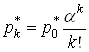, де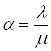

Тепер розглянемо -е рiвняння системи (15) i обчислимо ,

.

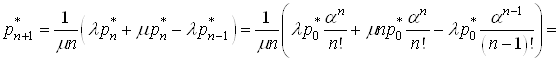
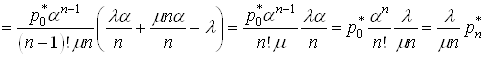Отже, одержали звтАЩязок Ваi

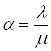Ваде (17)

Нехай формула (17) i правильною для . Необхiдно довести, що вона правильна i для . Для цього iз системи (15) вiзьмемо рiвняння з номером , отже

,

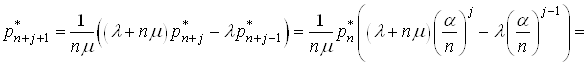
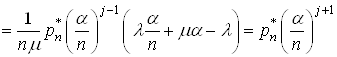тобто

.(18)

Тепер потрiбно перевiрити, що (18) правильна i для . Для цього необхiдно взяти останнi рiвняння системи (15), з нього маiмо

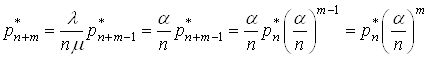.(19)

Таким чином, якщо порiвняти (18) i (19), можна записати:

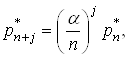
.(20)

Отже, 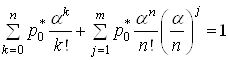, звiдки можна знайти , тобто, якщо врахувати формулу суми геометричноi прогресii ,

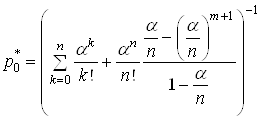(21)

2. Багатоканальнi СМО з очiкуванням без обмеження на довжину черги

система масове обслуговування очiкування черга

Для того, щоб скласти рiвняння для перехiдних iмовiрностей у випадку, коли СМО маi безлiч мiсць у накопичувачi, треба iз системи (14) викреслити останнi рiвняння i покласти . Питання iснування фiнальних ймовiрностей для такоi системи повтАЩязано з умовами, якi дають можливiсть виконуватися рiвностi , а це, якщо врахувати

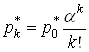, ,(22)

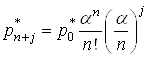, (23)

то (21) даi

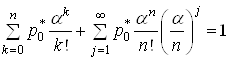.(24)

Другий доданок у (24) i нескiнченний ряд, який утворений iз геометричноi прогресii iз знаменником . Отже, для того, щоб вiн був збiжний, потрiбно, щоб . Це i умовою, для iснування фiнальних iмовiрностей , коли . З точки зору практичного використання цiii умови необхiдно, щоб середня кiлькiсть заявок, якi надходять до системи за середнiй час обслуговування однiii заявки одним каналом, була строго меншою нiж кiлькiсть каналiв. Тодi формула (21) спрощуiться:

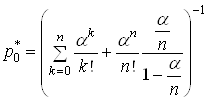Вапри умовi (25)

Основнi характеристики СМО з очiкуванням. Зупинимось на таких характеристиках СМО з очiкуванням, коли довжина черги нескiнченна, як середнi число заявок у черзi, середнi число заявок у СМО, функцiя розподiлу часу очiкування початку обслуговування, середнiй час перебування заявки
у СМО.

1. Середнi число заявок у черзi

Оскiльки число заявок в черзi i випадковою величиною iз значеннями
0, 1, 2, тАж i ймовiрностями вiдповiдно , тодi середнi число заявок у черзi i математичне сподiвання цiii величини, тобто:

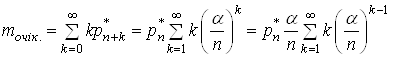.(26)

Для того, щоб знайти суму ряду 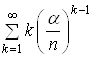, спочатку знайдемо суму ряду 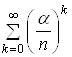, який утворено вiд геометричноi прогресii iз знаменником , тобто . Оскiльки останнiй ряд i степеневий ряд вiдносно , то вiн рiвномiрно збiгаiться для усiх , тому його можна почленно диференцiювати по . Тодi матимемо

(27)

Тепер врахуiмо (27) у рiвностi (26):

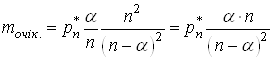,(28)

де 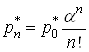Ваi Ваобчислюiться за формулою (25).

Середнi число заявок у СМО обчислюiться:

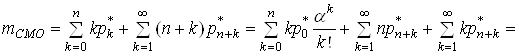
(29)

.

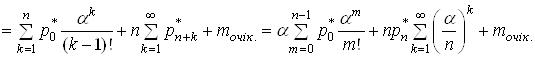Оскiльки

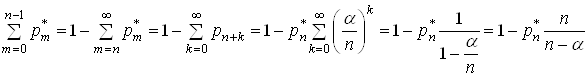
тодi (29) можна спростити:

.

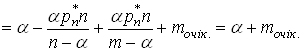Таким чином середнi число заявок у СМО i

,(30)

тобто складаiться iз середнього числа заявок, що находять за середнiй час обслуговування однiii заявки i середнього числа заявок, що очiкують у черзi.

3. Функцiя розподiлу часу очiкування початку обслуговування

Нехай Ваi випадкова величина часу, який заявка чекаi у СМО до початку обслуговування. Необхiдно визначити функцiю розподiлу цiii величини, тобто . Якщо використати визначення функцii розподiлу, то матимемо:

.

Знайдемо Вапри умовi, що час очiкування обслуговування Ваi випадкова подiя, коли усi канали вiльнi, чи коли зайнятий хоча б один з Ваканалiв, тобто

.

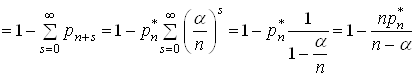Таким чином

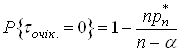(31)

Тепер обчислимо . По-перше, позначимо ймовiрнiсть Ватого, що за час Ваобслуговуватиметься бiльше нiж Вазаявок, при умовi, що зайнятi усi Ваканалiв. Крiм того, оскiльки потiк обслуговування заявок i пуассонiвським з параметром , то ймовiрнiсть обслуговування Вазаявок одним каналом обчислюiться за формулою .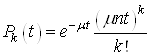

Якщо на обслуговуваннi два канали, тодi кожний канал обслуговуi одну заявку незалежно вiд другого. Отже ймовiрнiсть того, що Вазаявок будуть обслуженi двома каналами обчислюiться за формулою суми двох незалежних подiй

.

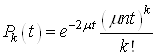Далi, продовжуючи аналогiчнi мiркування, можна записати таку формулу для ймовiрностi обслуговування за час Вазаявок, якщо Ваканалiв зайнятi:

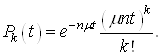(32)

Таким чином, якщо врахувати (32)

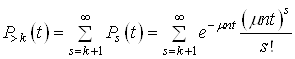(33)

Обчислимо ймовiрнiсть Ваза умови (33):

(34)

.

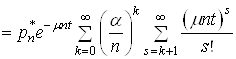В останнiй рiвностi помiняiмо порядок сумування змiнних Ваi . Тодi (34) можна записати у виглядi:

.

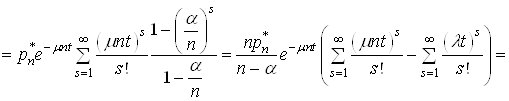
Тепер можна записати значення :

(35)

Враховуючи (31) i (35) до рiвностi (28) маiмо вираз для функцii розподiлу часу очiкування початку обслуговування у виглядi

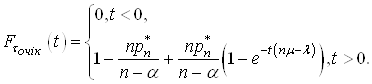(36)

Вираз (36) можна спростити i тодi:

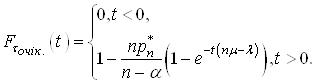(37)

Випадкова величина Ване i дискретною, бо в точцi Ваi 1 функцiя розподiлу Вамаi розрив. Якщо ввести функцiю 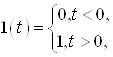Ващо маi похiдну 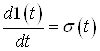, тодi можна записати щiльнiсть розподiлу часу очiкування обслуговування , тобто

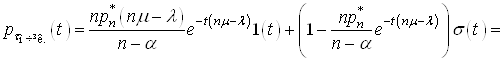
(38)

,

де .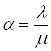

4. Середнiй час очiкування початку обслуговування

Якщо врахувати (38) i формулу обчислення математичного сподiвання випадковоi величини, тодi можна обчислити середнiй час очiкування початку обслуговування:

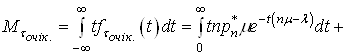
(39)

.

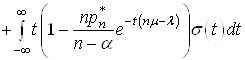Вiдомо, що 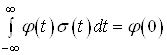, тому другий iнтеграл у (39) дорiвнюi нулю, тодi

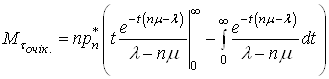.(40)

Оскiльки для iснування фiнальних ймовiрностей достатньо, щоб , тодi 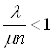, звiдки . Враховуючи це в (40), отримаiмо:

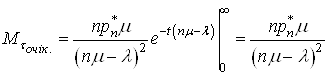.(41)

5. Середнiй час перебування заявки у СМО

Позначимо середнiй час перебування заявки в СМО через . Середнiй час перебування заявки в системi складаiться iз часу очiкування обслуговування i часу, що йде на обслуговування, тобто

,

тодi

.

Враховуючи (41) i те , що 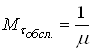, маiмо

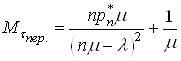. (42)

6. Функцiя розподiлу випадкового часу перебування заявки у СМО

(43)

,

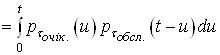де ВатАУ щiльнiсть розподiлу випадкового часу очiкування обслуговування, що обчислюiться за формулою (38), а ВатАУ щiльнiсть розподiлу випадкового часу обслуговування.

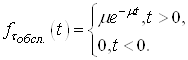
Вместе с этим смотрят:

GPS-навигация

IP-телефония. Особенности цифровой офисной связи

РЖсторiя звтАЩязку та його розвиток

Автоматика, телемеханика и связь

Анализ режимов автоматического управления